旋翼作为直升机主要的升力,推力和力矩操纵部件决定了直升机的飞行性能,尤其是气动性能. 对于旋翼整体的气动性能,桨叶剖面翼型外形有着决定性的作用,尤其是在桨叶中部和根部的外形设计上[1]. 翼型设计主要有反设计和优化设计2种方法[2]. 翼型反设计方法的优势在于可以根据事先给定的目标气动特性,通过不断求解迭代方程,从而设计出达到目标要求的气动外形,缺点在于目标气动特性的给定需要设计者丰富的设计经验. 对于优化设计方法,能够依据优化目标构建的目标函数,给定一定的限制条件,设计出符合要求的气动外形,在过去很长一段时间,得到了很多学者的关注,也取得了很重要的发展[3-4]. Jameson[5]发展了基于控制理论的伴随方法,开展气动外形的优化设计,该方法将物理边界作为控制函数,输出目标函数的梯度信息,并以此作为优化设计的基础. 伴随优化设计方法的主要特点是单次梯度信息求解计算量只相当于2倍的流场计算量,且与设计变量数目无关,这为复杂气动外形的优化设计提供了可能性[2].
直升机在前飞时,由于前行桨叶和后行桨叶的相对气流速度不同,导致桨盘两侧升力不均. 为了解决该问题,桨叶在前飞时会发生周期变距运动. 桨叶攻角的周期性变化导致后行桨叶中部和根部易发生动态失速现象. 动态失速会使得桨叶结构疲劳强度和飞行员操纵受到严重挑战,甚至会导致直升机坠毁. 针对旋翼的动态失速现象的旋翼翼型优化设计具有重要的理论和现实意义.
目前,针对旋翼翼型的动态失速特性的优化设计处于初步研究阶段. Mani等[6]在SC1095翼型的基础上,采用伴随方法进行动态失速特性的优化设计,优化结果显示,阻力系数和力矩系数的迟滞回线的峰值均有明显的下降,但是翼型的厚度增幅明显,这对于旋翼桨叶的减重是不利的,且翼型厚度增加会带来阻力发散马赫数的降低,这使得该翼型不适宜布局在旋翼桨叶的尖部. Wang等[7-8]采用基于梯度的序列二次规划算法和非定常Navier-Stokes方程求解器,对SC1095翼型和OA209进行非定常特性优化设计,虽然优化结果显示出了良好的动态失速抑制特性,但是在基于梯度的序列二次规划算法优化过程中,梯度算法会使得优化结果以一定几率陷入局部最优点,无法逼近全局最优解.
1. 动态失速数值模拟
1.1. 数值模拟方法
使用CFL3D[15]计算200个初始样本点,构建代理模型. CFL3D是NASA开发的非定常可压缩开源求解器,结合Spalart-Allmaras湍流模型,使用格心格式的有限体积法,求解雷诺平均Navier-Stokes方程. 网格界面无黏通量使用基于MUSCL格式重构的Roe近似黎曼求解器得到,黏性通量采用二阶中心格式计算,非定常时间项使用基于近似因式分解的隐式双时间步法离散. 远场使用基于一维黎曼不变量的无反射边界条件,物面使用无滑移边界.
使用商业软件Pointwise生成了计算网格,整体拓扑及局部细节如图1所示. 网格采用650(周向)×81(径向)的O型网格,半径约为60倍弦长,网格节点总数目为52 650,壁面第1层网格的无量纲高度为5×10−6,壁面附近网格高度的生长率为1.18,y+为1.3.
图 1
为了保持网格的正交性和光顺性,将网格作为一个整体固连于翼型上,随着翼型俯仰作刚性旋转运动,于是在计算过程中既保持了网格拓扑不变,又避免了网格变形带来的额外计算开销.
1.2. 数值模拟验证
图 2
图 2 升力系数、阻力系数和力矩系数数值模拟与实验对比结果图
Fig.2 Numerical simulation and experimental comparison of lift coefficient drag coefficient and moment coefficient
数值模拟的计算结果在上行部分与试验结果比较吻合,在下行部分有一定的偏差,下行部分主要是动态失速再附着的过程[17],动态失速下行部分的数值模型仅仅依靠二维非定常CFD计算是不够的,这是由于二维CFD计算自身的缺陷导致的. 动态失速再附着过程是三维强非线性过程,目前已有的建模方法不足以精确地模拟表达出该过程. 此外,从二维数值模拟结果可以看出,再附着阶段的升阻力和力矩的计算结果和试验数据存在一定的差距. 鉴于优化设计的时间成本,建立的二维数值模拟方法的计算结果可以支撑动态失速特性的优化设计.
2. 优化设计方法
2.1. 翼型参数化方法
采用CST[18]翼型参数化方法,上、下表面各采用5阶伯恩斯坦多项式,即6个设计参数,一共12个设计参数,进行翼型的变形和重构. 翼型的上、下表面函数可以表述如下:
式中:
表 1 初始翼型设计参数
Tab.1
| Ai | Ai | |||
| 上翼面 | 下翼面 | 上翼面 | 下翼面 | |
| 0.171 25 | 0.147 05 | 0.115 98 | 0.041 32 | |
| 0.157 34 | 0.068 40 | 0.170 30 | 0.141 48 | |
| 0.122 90 | 0.138 70 | 0.076 55 | 0.037 16 | |
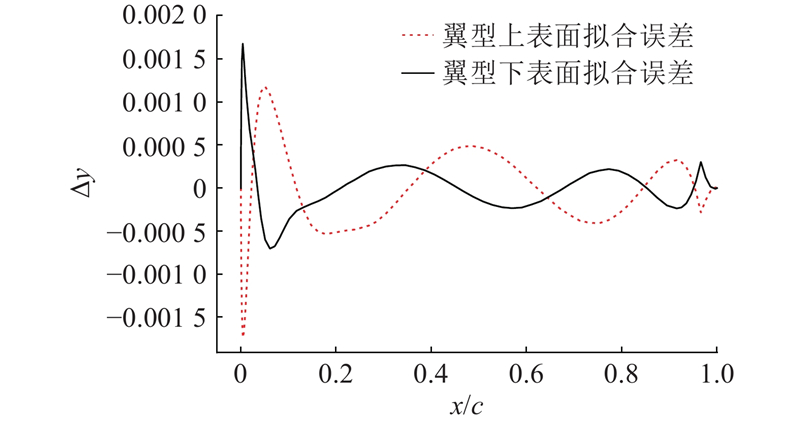
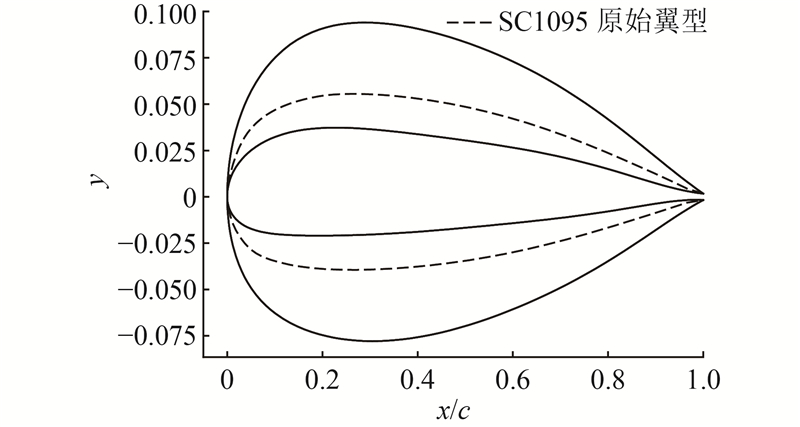
翼型参数化的结果如图3所示. 可以看出,基于CST的拟合外形与原外形吻合很好.
图 3
翼型参数化误差
图 4
图 4 类型转换参数化方法拟合误差图
Fig.4 Error evaluation diagram of class shape transformation method fitting
2.2. 代理模型的建立
2.2.1. 样本点的选取
代理模型的建立,首先需要一定的初始样本数据来训练代理模型,用以达到较好的预测结果.
图 5
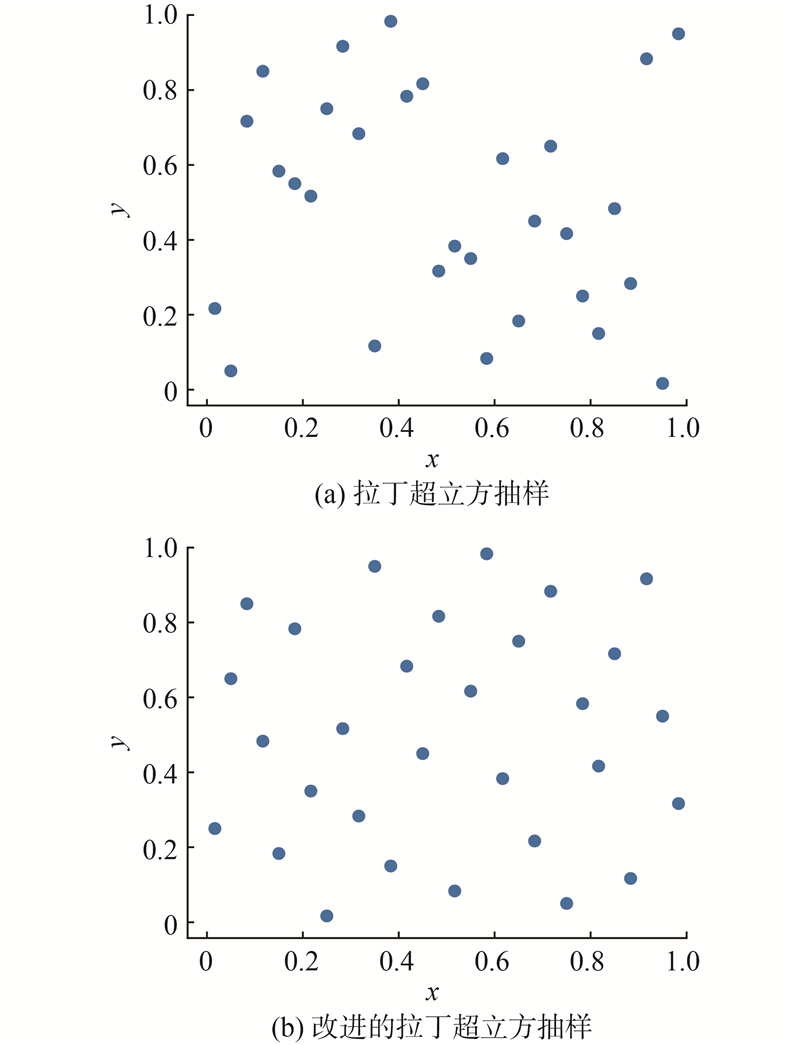
图 5 传统的和改进的拉丁超立方抽样方法对比图
Fig.5 Comparison results of conventional and improved Latin Hypercube Sampling methods
2.2.2. Kriging模型
Kriging模型是典型的插值模型[19],类似“黑箱”模型,也可以看作高斯过程回归模型. Kriging插值过程是一个随机过程,在设计空间内,随机插值响应存在一定的相关性. Kriging模型的预测响应可以写成如下形式,由一个常值
式中:
其中
选择的相关函数为高斯指数函数,表述如下:
式中:
式中:
Kriging模型可以给出预估值的均方差估计:
式中:
2.2.3. 加点准则
假设当前基于样本数据的目标函数最小值
目标函数改善量的期望值为
式中:Φ为标准正态分布累积分布函数,ω为标准正态分布概率密度函数.
本文的加点策略如下:在每次Kriging模型超参数优化过程中,寻找EI值最大和目标函数值最优的2个新的样本数据点加入模型训练优化中,直至得到一个更优的代理模型用于旋翼翼型优化. 加点策略的收敛终止条件如下:1)达到最大训练样本数量即停止,设置的最大训练样本为280个;2)代理模型预测相对误差低于收敛阈值[19]即停止,加点优化的收敛阈值设置为0.000 1.
2.2.4. 代理模型预测结果
为了验证建立的Kriging模型和EI加点准则适用于动态失速迟滞回线的预测,利用改进的拉丁超立方抽样方法,在如图6格子阴影部分的设计空间内选取200个初始样本数据,建立初代Kriging代理模型,样本的计算参数与图2的验证算例保持一致. 依据提出的加点策略,经过多轮超参数优化,在初始样本数据内增加了56个样本点,训练建立了最终Kriging模型. CFD计算结果、初代模型预测结果和经过加点准则后的最终模型预测结果对比如图7所示. 选取2个有代表意义的非训练样本空间测试点的升阻力迟滞回线预测对比用作展示代理模型超参数的优化过程,分别记为测试点1和测试点2. 对比结果显示,经过多轮超参数优化后,代理模型可以较准确地给出未知样本点的升阻力及力矩迟滞回线预测值. 在动态失速迟滞回线下行区域部分,由于初始样本数据中大量的样本都会出现不同程度的波动,致使下行区域的预测误差较大,但是预测结果的总体趋势是正确的,所以该预测结果可以进行有效的翼型优化设计.
图 6
图 7
图 7 测试点1和测试点2的Kriging模型初代和最终预测结果对比图
Fig.7 Comparison results of initial and final Kriging model prediction on test point one and two
Kriging模型预测的整体误差百分比E如表2所示. 表中,
表 2 初代和最终Kriging模型预测误差表
Tab.2
| 模型 | | | |
| 初代模型 | 10.67% | 8.72% | 12.38% |
| 最终模型 | 2.16% | 1.35% | 3.06% |
式中:N为一个周期的运动时间点数,Ns为测试样本数量,Vcfd为CFD计算值,Vpre为Kriging模型预测值.
2.3. 优化流程
本文的优化目标是为了减少旋翼翼型的阻力和力矩系数迟滞回线的峰值,约束条件是保证升力系数不降低以及翼型厚度在初始翼型厚度的合理倍数以内. 具体目标函数和约束条件将在具体算例下给出.
1)依据初始翼型参数化参数和设计空间,随机生成初始群体,群体规模记为P.
2)由事先训练好的最终Kriging代理模型对每一个个体进行评估,从中随机选择3个个体,将其中2个个体作差,再乘以缩放因子F加到另一个个体上,这一步是变异操作. 这是差分进化算法的核心.
3)变异操作后进行交叉操作,交叉是为了增加群体的多样性,交叉阈值CR须事先给定.
4)为了确定群体内每一个个体能否成为下一代成员,需要根据目标函数和约束条件进行选择操作.
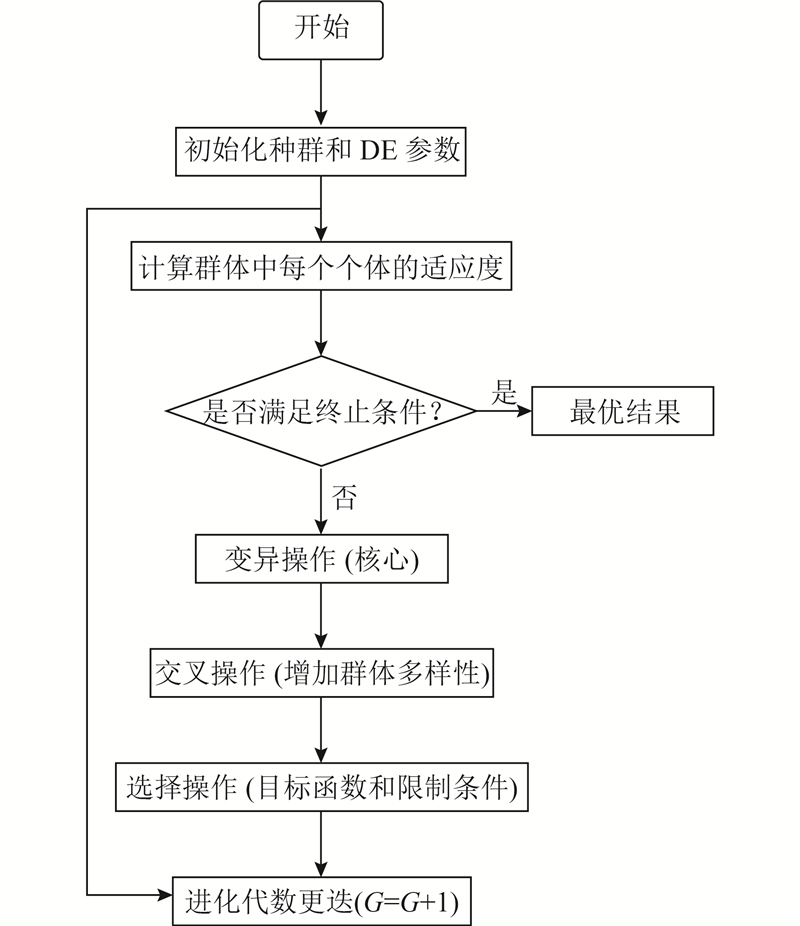
5)反复执行2)~4),直至达到最大的进化代数G;整体算法的优化流程如图8所示.
图 8
图 8 差分进化算法的优化流程图
Fig.8 Differential evolution algorithm optimization flow chart
设置P=15,F=0.7,CR=0.5,最大进化代数为100,收敛阈值设置为0.001,优化过程只需达到最大进化代数或目标函数值的相对误差低于收敛阈值[19]即满足停止条件,整个优化过程只需短短几十秒.
3. 优化结果与分析
3.1. 算例1
算例1的物理条件设置与Mani等[6]利用伴随方法对SC1095翼型进行动态失速特性优化设计的算例设置保持一致,只修改了目标函数的形式. 来流马赫数为0.302,雷诺数为3.89×106,缩减频率为0.148. α0=9.92°,α1=9.90°. 修改后的目标函数和限制条件总结如下.
式中:所有带有下标0的变量表示初始值,其余变量表示优化过程中每一步的具体数值. 算例1采取给定单目标权值的方法,将多目标优化转化为单目标优化,鉴于翼型的力矩系数在多数情况下稍小于阻力系数,故在目标函数中给定力矩系数计算部分0.6的权值系数,阻力系数部分0.4的权值系数.
因为受自然进化启发的算法,种群初始化的随机性导致每一次优化的目标函数评价次数和进化代数均不一样. 通过采用的优化策略和参数设置,优化算例1的目标函数一般在69~75代达到收敛,目标函数评价次数约为14 000,每次优化结果十分接近. 利用代理模型建立的初始样本数据为200个,后经EI加点准则,利用Kriging模型建立成功的样本数据为256个. 升力系数的整体误差为2.163 5%,阻力系数误差为1.355 0%,力矩系数误差为3.061 5%.
表 3 算例1的原始翼型与优化翼型细节参数对比表
Tab.3
| 翼型 | 最大厚度 | 最大厚度位置 | 弯度 | 前缘半径 |
| 原始翼型 | 9.5% c | 26.9% c | 0.81% c | 0.77% c |
| 优化翼型 | 11.80% c | 24.3% c | 3.27% c | 2.80% c |
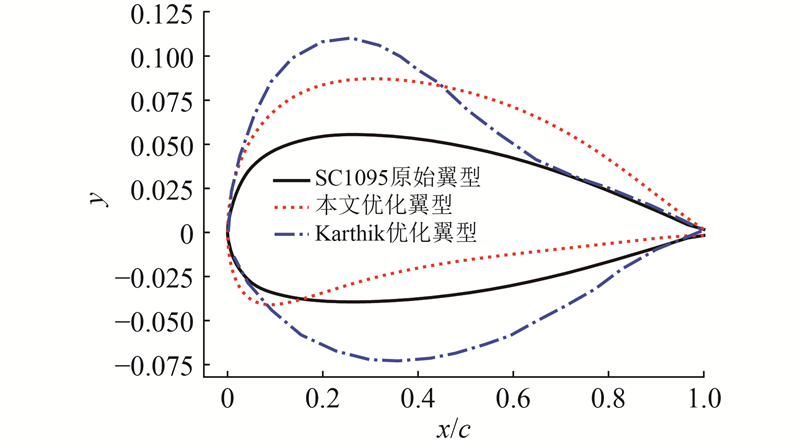
图 9
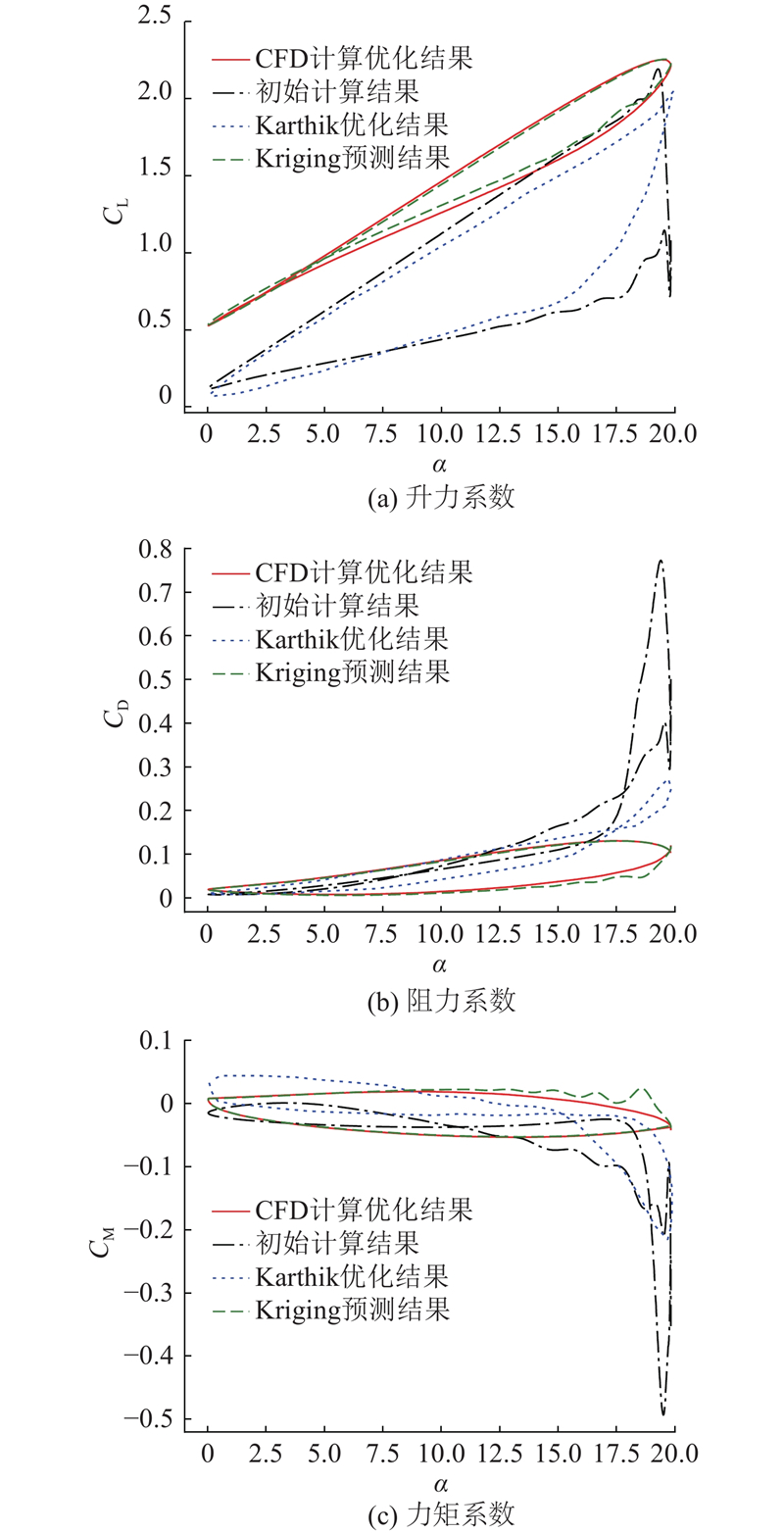
图10给出升阻力和力矩迟滞回线的对比结果,此外给出优化翼型的Kriging模型预测结果. 从阻力和力矩迟滞回线可以看出,优化后的翼型具有更优的气动性能,峰值下降相比于Karthik的优化结果更明显,本文优化翼型的升力特性更优,明显抑制甚至消除了深失速现象,迟滞回线呈现相对平缓的过渡状态. Kriging模型对优化翼型的预测结果表明,利用该代理模型可以较好地预测翼型外形变化带来的迟滞曲线变化,唯一不足的是下行区域的预测精度不足,这是由于CFD样本数据中下行区域均存在一定的数值波动.
图 10
图 10 算例1的升力、阻力和力矩系数气动特性结果对比图
Fig.10 First example comparison results of aerodynamic characteristics in lift,drag and moment coefficient
图11分别给出当来流攻角为15.05°时,原始翼型和优化翼型的马赫数云图和流线的对比图. 流场对比显示,优化翼型的绕流流场更平缓,明显抑制了前缘涡的强度. 流线图显示,优化翼型的前缘涡远远小于初始翼型的前缘涡. 前缘涡的减弱,从另一方面解释了动态优化翼型的升阻力及力矩系数迟滞回线平缓的变化状态.
图 11
图 11 算例1的动态优化翼型和初始翼型流场对比图
Fig.11 First example comparison of airfoil flow field of unsteady optimized airfoil with original airfoil
算例1的优化对比结果表明,基于代理模型和全局优化算法的动态优化设计具有更好的寻优性能,可以在未加厚度约束的情况下得到相对更好的气动外形,从而抑制甚至消除旋翼翼型的深失速现象.
3.2. 算例2
表 4 算例2原始翼型与优化翼型细节参数对比表
Tab.4
| 翼型 | 最大厚度 | 最大厚度位置 | 弯度 | 前缘半径 |
| 原始翼型 | 9.5% c | 26.9% c | 0.81% c | 0.77% c |
| 优化翼型 | 9.97% c | 14.7% c | 3.95% c | 2.43% c |
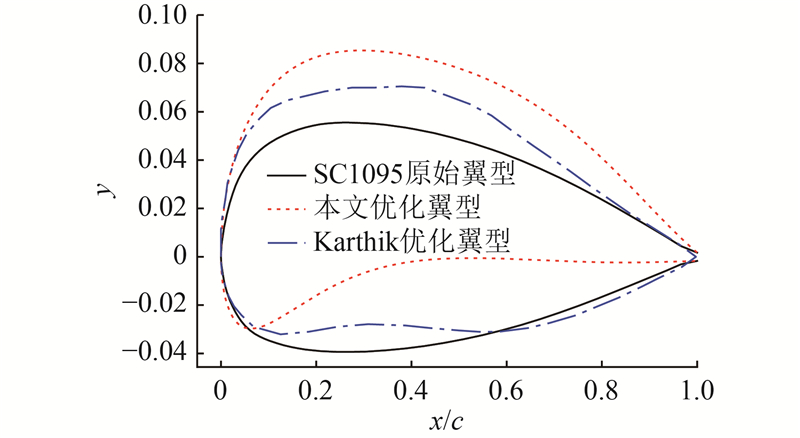
图 12
图 12 算例2的动态失速优化翼型对比
Fig.12 Second example comparison of dynamic stall optimization airfoil
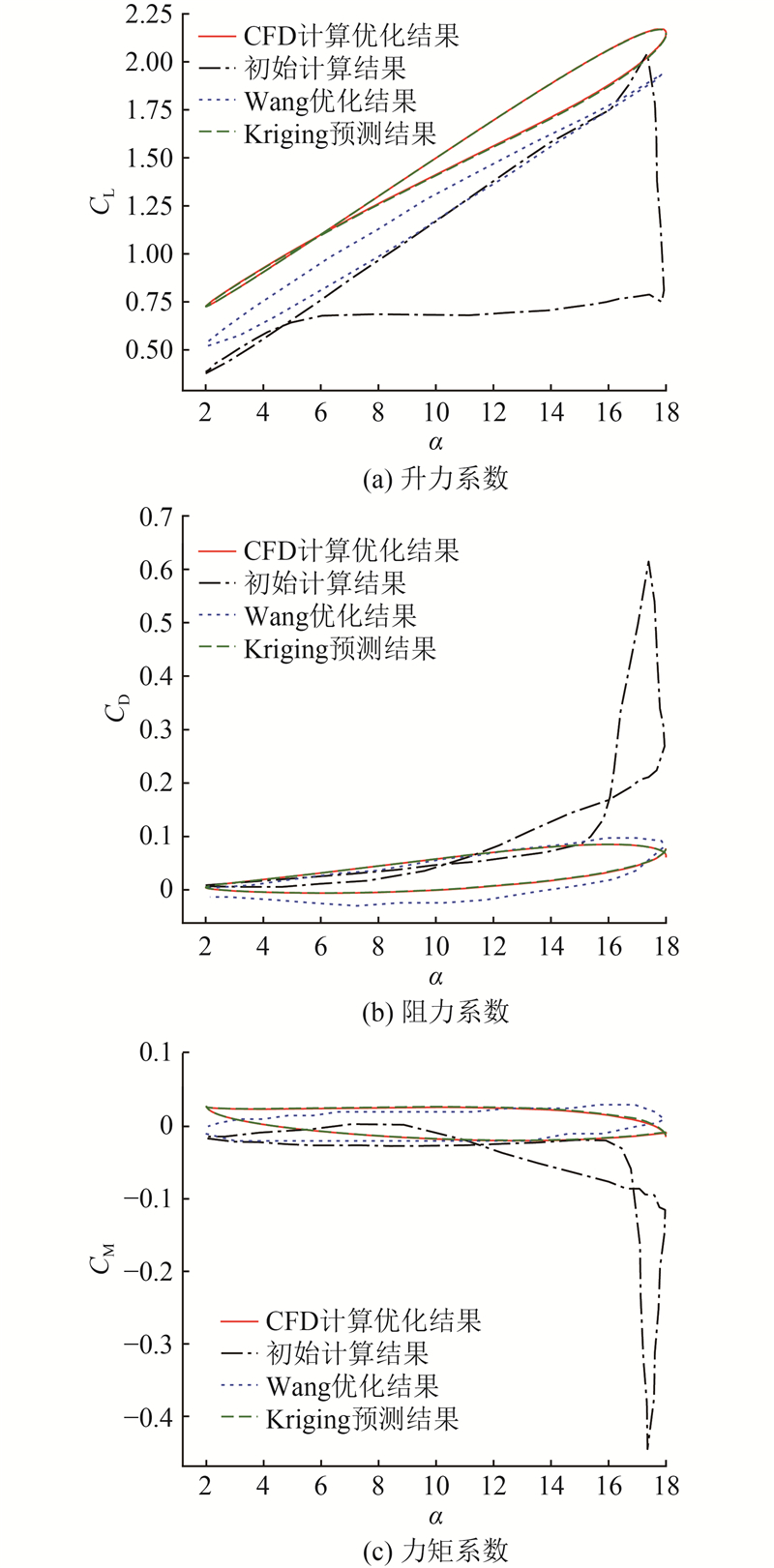
图 13
图 13 算例2的升力、阻力和力矩系数气动特性结果对比图
Fig.13 Second example comparison results of aerodynamic characteristics in lift,drag and moment coefficient
图14给出优化翼型和原始翼型在来流攻角为17.77°时的马赫数云图和流线图. 从流场特征可以看出,优化翼型由于较大的前缘半径和弯度,前缘涡几乎消除,只在尾缘处存在一个强度较小的涡场. 这解释了该算例的优化结果是有效的.
图 14
图 14 算例2的动态优化翼型和初始翼型流场对比
Fig.14 Second example comparison of airfoil flow field of unsteady optimized airfoil with original airfoil
在全局优化算法框架下,算例2调用代理模型17 000次左右,若使用CFD方法进行17 000次气动评价,则优化的时间成本是无法估量的. 基于梯度的翼型优化,需要人为给定一个较优的外形,这样可以避免过早地陷入局部最优点. 直接使用代理模型和全局优化算法可以选择更大的优化空间,这对于动态失速特性的优化是十分有利的.
4. 结 论
(1)建立动态失速特性预测的Kriging模型方法和加点准则是有效的,预测精度可以满足优化设计的需求.
(2)结合基于Kriging的动态失速代理模型和全局优化算法,开展旋翼翼型的优化设计. 优化结果表明,基于代理模型动态失速特性优化设计是可行的,且可以在更大的设计空间内找到全局最优解.
(3)基于代理模型的动态失速特性优化,与基于伴随方法的动态失速特性优化相比,由于前者易于给定多个限制条件,优化翼型的升力特性表现更好,阻力和力矩迟滞回线峰值得到明显的降低,动态失速特性得到有效的抑制.
(4)在与基于CFD方法的动态失速特性优化设计对比中,在阻力和力矩特性表现相差无几的条件下,升力特性表现更好. 这说明基于代理模型和差分进化算法的优化设计方法,可以在更大的优化设计空间内,找到气动全局最优解.
参考文献
Aerodynamic design optimization of helicopter rotor blade design including airfoil shape for hover performance
[J].DOI:10.1016/j.cja.2012.12.008 [本文引用: 1]
基于级联前向网络的翼型优化设计
[J].
Aerodynamic optimization design of airfoil configurations based on cascade feedforward neural network
[J].
基于改进多目标布谷鸟搜索算法的翼型多目标气动优化设计
[J].
An improved multi-objective cuckoo search algorithm for airfoil aerodynamic shape optimization design
[J].
Aerodynamic design via control theory
[J].DOI:10.1007/BF01061285 [本文引用: 1]
Aerodynamic shape optimization for alleviating dynamic stall characteristics of helicopter rotor airfoil
[J].DOI:10.1016/j.cja.2014.12.033 [本文引用: 8]
Rotor airfoil profile optimization for alleviating dynamic stall characteristics
[J].DOI:10.1016/j.ast.2017.11.033 [本文引用: 1]
基于Kriging模型的翼型气动性能优化设计
[J].DOI:10.3321/j.issn:1000-6893.2005.05.004 [本文引用: 1]
Aerodynamic optimization design for airfoil based on Kriging model
[J].DOI:10.3321/j.issn:1000-6893.2005.05.004 [本文引用: 1]
改进Kriging模型在翼型气动优化设计中的应用研究
[J].
Application of improved kriging-model-based optimization method in airfoil aerodynamic design
[J].
Optimal Latin-hypercube designs for computer experiments
[J].
Efficient global optimization of expensive black-box functions
[J].DOI:10.1023/A:1008306431147 [本文引用: 2]
Differential evolution: a Simple and efficient heuristic for global optimization over continuous spaces
[J].DOI:10.1023/A:1008202821328 [本文引用: 2]
Development of reduced-order models for aeroelastic analysis and flutter prediction using the CFL3Dv6.0 code
[J].
Experimental investigation of the flow field of an oscillating airfoil and estimation of lift from wake surveys
[J].
Dynamic stall in pitching airfoils: aerodynamic damping and compressibility effects
[J].DOI:10.1146/annurev-fluid-010814-013632 [本文引用: 1]
Universal parametric geometry representation method
[J].
Kriging模型及代理优化算法研究进展
[J].
Kriging surrogate model and its application to design optimization: a review of recent progress
[J].