随着城市交通拥堵问题的日益加剧,公共交通作为大容量、低排放的交通出行工具,在缓解城市交通拥堵中的作用举足轻重,公交优先政策得到社会的普遍关注. 路口公交延误是衡量公交运行状态的关键指标之一[1],通过有效合理地减少交叉口公交延误,将大大提高公交出行的吸引力,促使小汽车使用人群向公交转移. 本文旨在建立考虑路口上游停靠站影响的公交延误模型,通过模型测算近交叉口公交延误,可以进一步为公交站点的选址优化、公交运行状态评价等方面提供相关的理论依据.
目前,对于路口停靠站影响下的公交延误研究主要集中于以下2个方面:站点停靠延误方面和站点对交通流的影响方面. 前者主要考虑停靠站自身运行效率的影响,后者侧重考虑停靠站的设置对路段通行能力及车流延误的影响. 在停靠延误方面,Alonso等[2]考虑乘客上下车及车辆排队引起的站内停靠延误;杨晓光等[3]基于排队论与间隙接受理论,建立公交车辆进出直线式和港湾式停靠站对机动车道的影响时间模型. 武钧等[4]以公交车到达率、站点通行能力、泊位数和信号参数为解释变量,建立可超车条件下的站点延误模型. 在对通行能力及车流影响方面,Gu等[5-6]针对直线式公交停靠站设置在路口上游时,研究站点对公交车和社会车辆的延误影响,建立相应的延误模型;Ge等[7-8]通过分析不同条件下公交车停靠对信号交叉口车辆的影响机理,建立公交车停靠影响下的交叉口进口车辆延误模型. 孙锋等[9-11]利用排队论和间隙理论,推导了直线式和港湾式站点路段的通行能力计算模型. 郑锐等[12]针对上游停靠站公交溢出影响下,建立交叉口进口道的通行能力损失模型,对路口乘客延误进行修正. 除了上述通过数学模型分析的方法外,目前越来越多的人通过元胞自动机[13-15]、VISSIM微观仿真[16-17]等方法,研究跟随公交车行驶的车辆车道变换及交通状态的变化过程,结合统计分析给出公交停靠站点影响下的车辆运行特性.
上述交叉口公交延误研究大体直接运用交叉口的车辆延误计算公式,较少考虑公交站点停靠及交叉口车辆排队的联合阻滞影响,其准确性受到很大程度的制约. 为了弥补现有成果所存在的上述缺陷,本文对路口上游停靠站位置、信号配时、公交停靠时间等因素进行系统分析,在相关研究的基础上建立路口上游停靠站影响的公交延误模型,通过数值模拟对模型进行分析测算.
1. 场景分类与基本假设
1.1. 基本概念说明
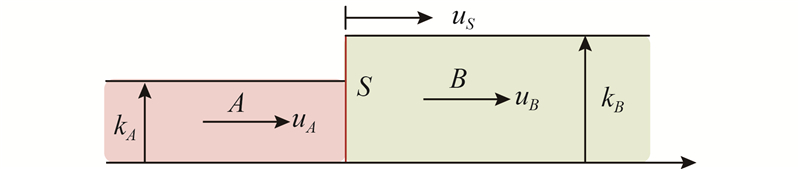
图 1
由交通流量守恒可知,在时间
式中:
根据交通流参数基本关系式
假设某一交叉口为固定信号配时,且交叉口车流量为非饱和态,即保证每个周期内清空剩余排队. 在考虑交通波的影响下,绿灯启亮时,交叉口的排队车辆开始消散,当排队产生的消散波与停车产生的停车波相遇时,此时波阵面所处的位置为该交叉口的最远排队点,对应的最远排队距离
式中:
由式(3)可得,
综上所述,
1.2. 场景分类与假设
本文的建模场景主要依据系统中是否设置公交专用道以及公交站点位置是否大于交叉口最远排队点这2个基本原则来进行分类.
1)BL场景:系统设有公交专用道时的场景,公交车与社会车辆相互独立运行,无论站点位置设置如何,公交车在站点的进站、停靠、出站等行为不受其他社会车辆的影响,公交运行相对独立.
2)NBL场景:系统不设公交专用道时的场景,公交车与社会车辆混行,公交车在路口将会遇到车辆排队. 在该场景中,结合公交站点与交叉口最远排队点的位置关系,可以细分为2种情景. NBL1场景:公交站点离停车线的距离
在分析各场景下公交延误之前,假定路口公交延误为公交车实际驶离路口所需时间与其以自由流车速驶离路口所需时间之差. 有如下假设:1)路口流量为非饱和态,保证每个周期内清空剩余排队;2)不考虑车辆启停过程中的加减速的影响;3)路口为固定信号配时,周期时长为
2. BL场景下的公交延误分析
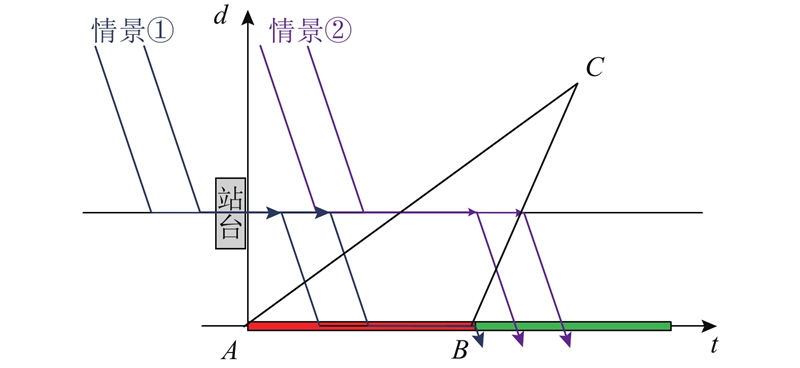
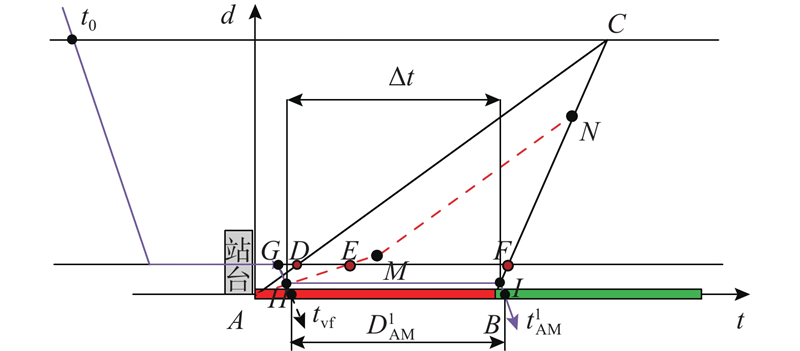
在BL场景中,由于公交专用道的设置,路口红灯期间的车辆排队对公交车辆的运行无影响,公交车运行相对独立. 在该场景中,根据公交车达到路口停车线的时刻,可以分为以下2种情景:1)公交车到达停车线的时刻为红灯;2)公交车到达停车线的时刻为绿灯. 具体的交叉口车辆运行时空图如图2所示. 图中,虚线表示交叉口车辆排队的形成与消散的过程,实线表示交叉口附近公交车的运行轨迹.
图 2
图 2 BL场景下的交叉口车辆运行时空图
Fig.2 Space-time map of intersection vehicles under BL scenario
情景1):公交车到达停车线的时刻介于红灯时长AB之间. 当红灯启亮时,公交车到达交叉口停车线,即图2的A点时刻,此时公交车延误最大,等于交叉口红灯时长;当公交车到达交叉口停车线时刻为B点时,此时红灯结束,绿灯启亮,公交车无延误直接通过交叉口. 假设公交车离散到达,在该情景下公交车的平均排队延误为
在一个周期内,情景1)发生的概率可以表示为
情景2):当公交车到达停车线的时刻为绿灯时间,此时公交车均无延误直接通过交叉口,公交车的平均排队延误
综上所述,在BL场景中,交叉口公交车的期望延误可以表示为
3. NBL场景下的公交延误分析
3.1. NBL1场景
在NBL场景中,公交车与小汽车相互混行,公交车通过交叉口所需的时间将受到交叉口车辆排队的影响. 当
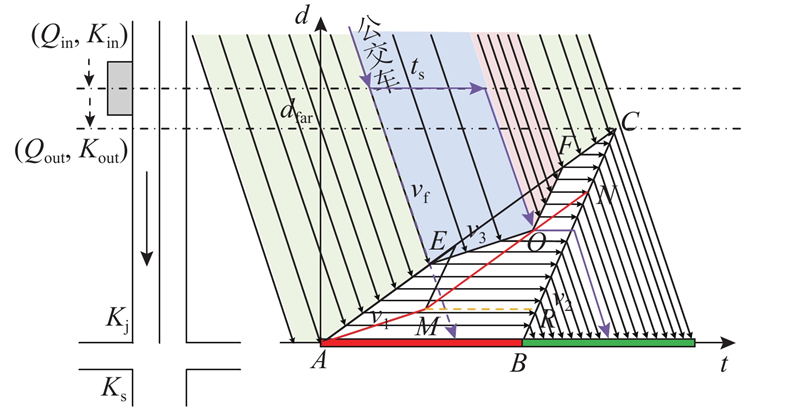
系统中公交车以自由流车速
图 3
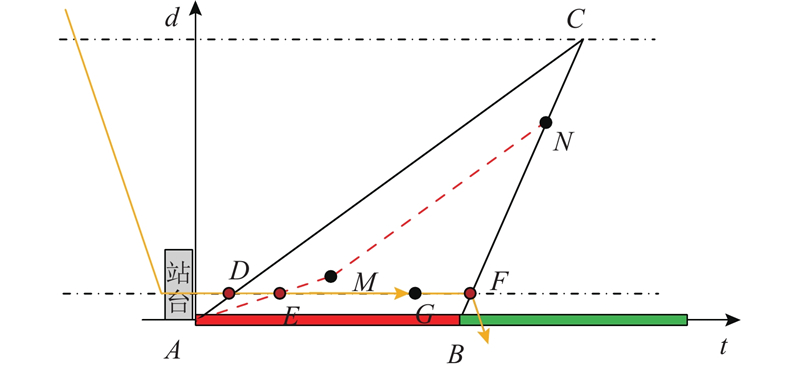
图 3 NBL1场景下的交叉口车辆运行时空图
Fig.3 Space-time map of intersection vehicles under NBL1 scenario
在该过程中,假设该进口道的交通需求为
式中:
式中:
1)时空点O在线段A-M上.
当O点与A点重合时,此时公交车交叉口排队延误最大,其值等于
由于公交离散到达,可以认为时空点O在线段A-M上任意一点的概率相等,此时公交车的平均排队延误
在满足时空点O在线段A-M上的条件下,通过计算在单信号周期内公交车到达停车线的时间范围
2)时空点O在线段M-N上.
当O点与N点重合时,此时公交车无排队延误;当O点与M点重合时,公交车交叉口排队延误最大,其值等于
该种情景发生的概率
3)公交车到达交叉口无需排队等待.
该情景下的公交车在交叉口绿灯时间到达,且无需排队直接通过交叉口,因此平均排队延误
综上所述,NBL场景下的交叉口公交期望延误
3.2. NBL2场景
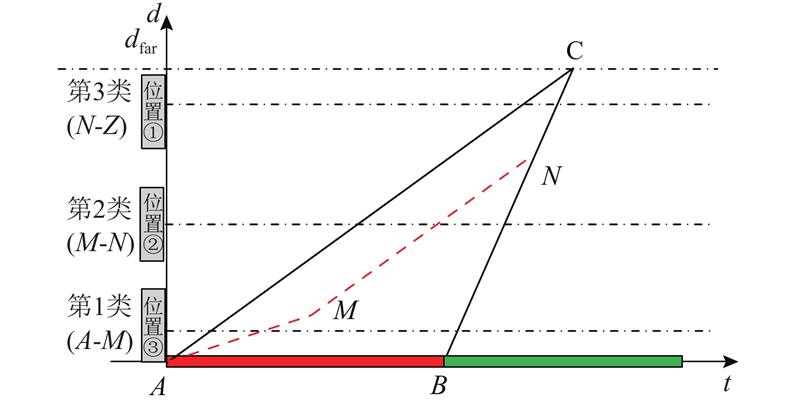
当
图 4
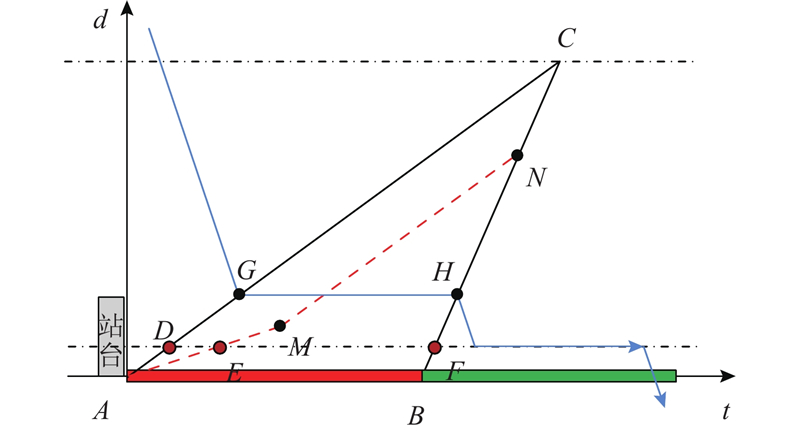
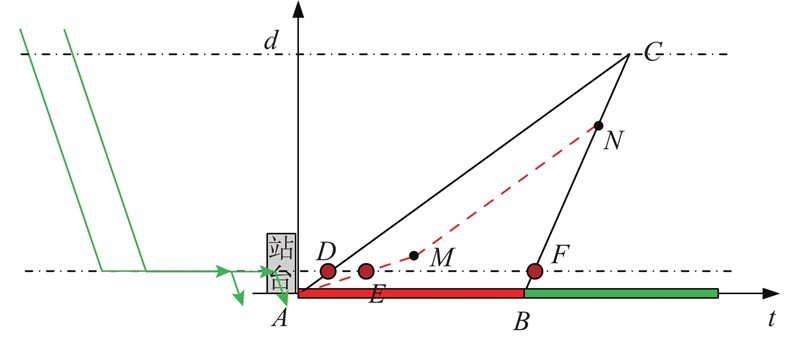
图 4 NBL2场景下的交叉口车辆运行时空图
Fig.4 Classification of different bus stop locations under NBL2 scenario
3.2.1. ${d_{\rm{A}}} \leqslant {d_{\rm{s}}} < {d_{\rm{M}}}$
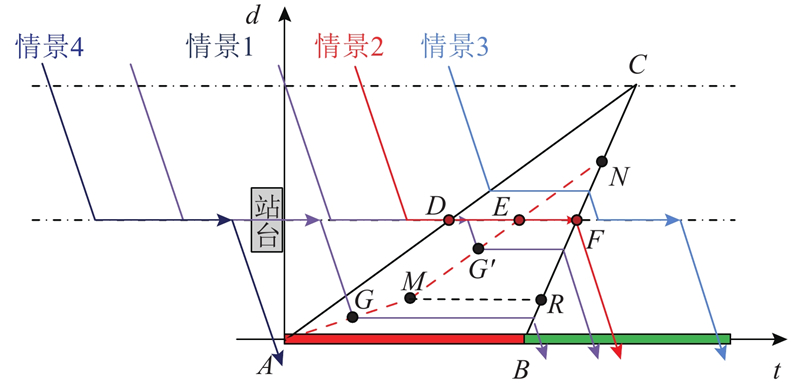
根据公交车到达公交站点以及驶离交叉口的不同时刻,可以将公交车的运行轨迹划分为如下4种情景. 情景1):公交车自由行驶至站点,停靠结束后自由驶离站点,加入交叉口排队;情景2):公交车自由行驶至站点,停靠期间交叉口排队上溯至站点,公交车在站等待绿灯排队释放,驶离交叉口;情景3):由于排队上溯,公交车无法直接进站而加入交叉口排队,待排队消散,进站停靠,出站后自由驶离;情景4):公交车绿灯时期自由到达站点,停靠后自由驶离交叉口,无需交叉口排队.
情景1):公交车自由行驶至站点,当停靠结束时的时空点G在E点的左侧时,公交车自由驶离站点并加入交叉口排队,其公交车的运行轨迹如图5所示. 假设公交车进入系统的初始时刻
图 5
图 5
当
Fig.5
Bus operation trajectory of scenario 1 when
式中:
根据图5中的几何关系,可以推导出时空点H的坐标:
由式(23)可得,情景1)中的公交车在路口的排队等待时间
公交车实际通过交叉口的时刻
综上所述,情景1)中的交叉口公交延误
此时,
情景2):公交车自由行驶至站点,当时空点G在E点的右侧时,交叉口排队车辆上溯至站点,并当时空点G满足在F点的左侧时,由于交叉口排队的影响,公交车需要在站点等待绿灯排队释放;当时空点G在F点的右侧时,公交车辆直接驶离交叉口. 情景2)下的公交车运行轨迹如图6所示.
图 6
图 6
当
Fig.6
Bus operation trajectory of scenario 2 when
该情景下的公交实际通过交叉口的时刻
情景2)中的交叉口公交延误
此时,
情景3):由于交叉口排队上溯,公交车无法直接自由进站,而先加入交叉口排队,待绿灯启亮排队消散后,进行进站停靠,出站后自由驶离交叉口. 情景3)下的公交车运行轨迹如图7所示.
图 7
图 7
当
Fig.7
Bus operation trajectory of scenario 3 when
情景3)下公交实际通过交叉口的时刻
因此,情景3)中的交叉口公交延误
情景4):公交车绿灯时期自由到达公交站点,停靠后自由驶离交叉口,无需交叉口排队,情景4)下的公交车运行轨迹如图8所示. 此时公交实际通过交叉口的时刻
图 8
图 8
当
Fig.8
Bus operation trajectory of scenario 4 when
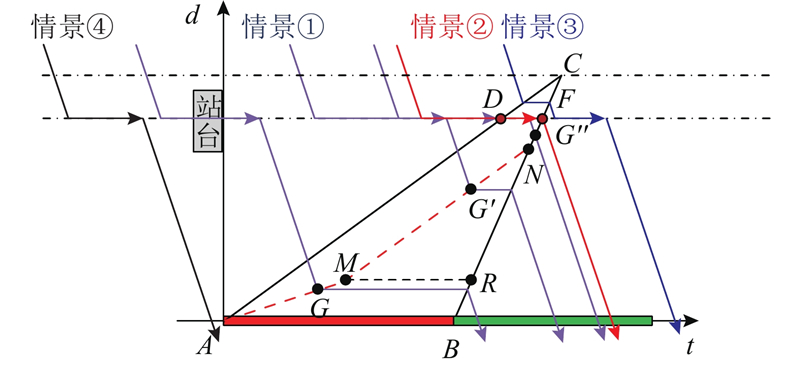
3.2.2. ${d_{\rm{M}}} \leqslant {d_{\rm{s}}} < {d_{\rm{N}}}$
与站点满足
图 9
图 9
当
Fig.9
Bus operation trajectory map under different scenarios when
情景1):公交车自由行驶至站点,停靠结束后自由驶离站点,加入交叉口排队. 与
式中:公交车加入交叉口的排队时空点
该情境下的
情景2):公交车自由行驶至站点,在停靠期间排队上溯至站点,公交车在站等待绿灯排队释放,该情景下的交叉口公交延误
情景3):公交车先加入交叉口排队,无法直接进站,待排队消散后进站停靠,出站后自由驶离. 该情景下的交叉口公交延误
情景4):公交车绿灯时期自由到达站点,停靠后自由驶离交叉口,无交叉口排队,该种情景下的交叉口公交延误
3.2.3. ${d_{\rm{N}}} \leqslant {d_{\rm{s}}} < {d_{\rm{C}}}$
与前述2种情况相似,根据公交到达站点以及驶离交叉口的不同时刻,可以将公交车的运行轨迹划分为4种情景,如图10所示.
图 10
图 10
当
Fig.10
Bus operation trajectory map under different scenarios when
情景1):公交车自由行驶至站点,停靠结束后自由驶离站点,加入交叉口排队. 与
式中:时空点
该情境下的
情景2):公交车自由行驶至站点,在停靠期间排队上溯至站点,公交车在站等待绿灯排队释放. 该情景下交叉口公交延误
情景3):公交车先加入交叉口排队,无法直接进站,待排队消散后进站停靠,出站后自由驶离. 该情景下交叉口公交延误
情景4):公交车绿灯时期自由到达站点,停靠后自由驶离交叉口,无交叉口排队. 该种情景下的交叉口公交延误
4. 数值分析
假设交叉口的基础属性如下:进口道车道数为3条,单车道
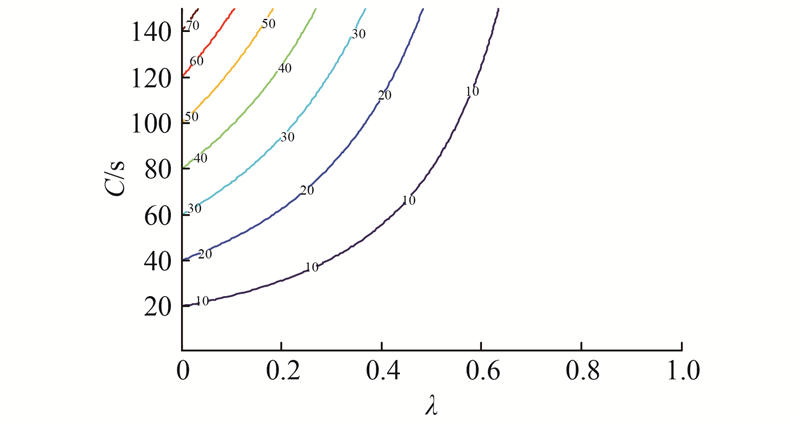
1)BL场景. 由式(9)可知,该场景下的延误
图 11
图 12
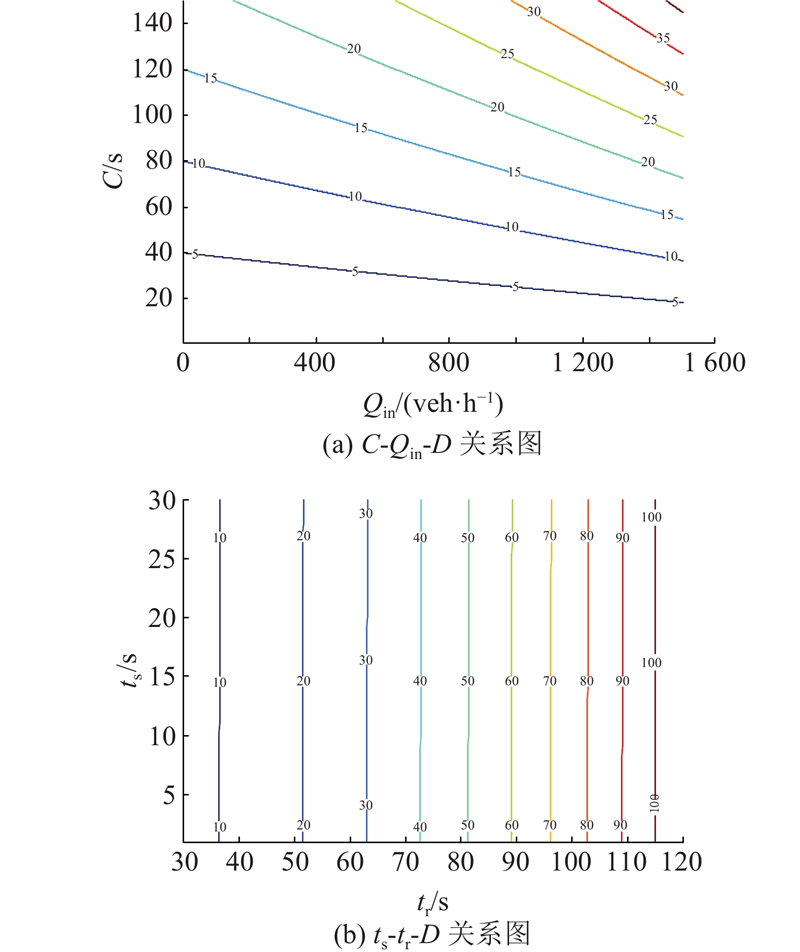
同理,在图12(b)中考虑
3)NBL2场景. 图13(a)中设置C为120 s,λ=0.5,
图 13
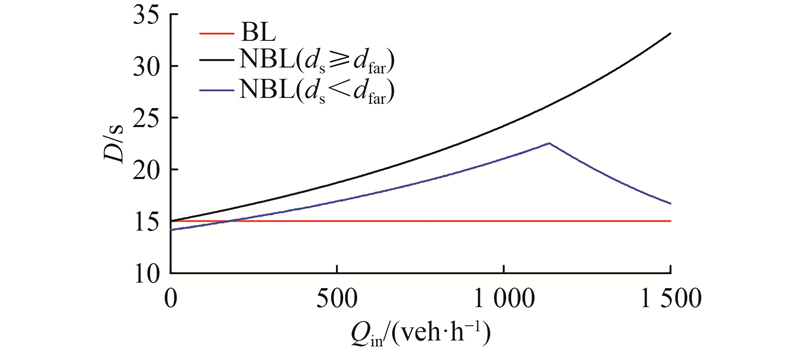
4)
图 14
图 14 3种场景下的输入流量-延误影响
Fig.14 Impact of input traffic on delays in three scenarios
5. 结 语
本文在交通波的基础上,针对交叉口有无公交专用道的不同场景,分别建立站点影响下的近交叉口公交延误模型. 通过计算机数值模拟,分析站点位置、信号配时、停靠时间、流量等因素对交叉口公交延误的影响. 本文模型忽略公交进出站的影响,且未对模型进行实际的数据验证. 未来可以考虑细化模型的影响因素,利用实际数据进行参数标定,研究近交叉口的公交站点优化布设问题,为公交站点选址的定量分析提供理论依据.
参考文献
Valuing transit service quality improvements
[J].DOI:10.5038/2375-0901.11.2.3 [本文引用: 1]
Analytical model for calibrating delay at congested bus stops
[J].DOI:10.1080/03081060.2013.830893 [本文引用: 1]
单车道港湾式公交停靠站设置条件研究
[J].DOI:10.3969/j.issn.1002-0268.2010.12.022 [本文引用: 1]
Study of setting conditions of bus bay stop of single lane
[J].DOI:10.3969/j.issn.1002-0268.2010.12.022 [本文引用: 1]
可超车条件下公交车站点延误估算模型研究
[J].
Modelling bus delay at bus stop under bus overtaking maneuvers permitted
[J].
Mitigating negative impacts of near-side bus stops on cars
[J].DOI:10.1016/j.trb.2012.09.005 [本文引用: 1]
On the impacts of bus stops near signalized intersections: models of car and bus delays
[J].DOI:10.1016/j.trb.2014.06.001 [本文引用: 1]
Traffic delay at signal-controlled intersection with bus stop upstream
[J].
信号交叉口上游公交站点实际停靠延误模型
[J].DOI:10.3321/j.issn:0367-6234.2008.12.045 [本文引用: 1]
Bus stopping delays at signal controlled intersection with bus stops upstream
[J].DOI:10.3321/j.issn:0367-6234.2008.12.045 [本文引用: 1]
直线型公交停靠站通行能力计算方法
[J].DOI:10.3969/j.issn.0258-2724.2013.03.024 [本文引用: 1]
Method for computing on-line bus stop capacity
[J].DOI:10.3969/j.issn.0258-2724.2013.03.024 [本文引用: 1]
公交站点对路段通行能力的影响研究
[J].DOI:10.3969/j.issn.1001-0645.2013.12.015
Study of the effect of the bus stop on roadway link capacity
[J].DOI:10.3969/j.issn.1001-0645.2013.12.015
港湾式公交停靠站通行能力计算方法
[J].
Method for calculating the capacity of bus bay
[J].
上游停靠站公交溢出影响下交叉口公交优先配时优化
[J].
Study on the method of bus priority signal timing at intersections under the influence of bus overflowing
[J].
The capacity drop caused by the combined effect of the intersection and the bus stop in a CA model
[J].DOI:10.1016/j.physa.2007.07.040 [本文引用: 1]
The capacity of two neighbour intersections considering the influence of the bus stop
[J].DOI:10.1016/j.physa.2008.03.011
公交车站对交通流影响模拟分析
[J].DOI:10.3321/j.issn:1000-3290.2009.10.030 [本文引用: 1]
The influence of bus stop on the dynamics of traffic flow
[J].DOI:10.3321/j.issn:1000-3290.2009.10.030 [本文引用: 1]
基于VISSIM仿真的公交停靠时间对交叉口延误影响研究
[J].
Study on the influence of bus dwell time on intersection delay based on VISSIM simulation
[J].
Modelling the net traffic congestion impact of bus operations in Melbourne
[J].DOI:10.1016/j.tra.2018.08.005 [本文引用: 1]