浙江大学学报(工学版)

浙江大学学报(工学版), 2020, 54(4): 759-766 doi: 10.3785/j.issn.1008-973X.2020.04.015

土木工程、交通工程

合肥膨胀土动弹性模量与阻尼比试验研究

庄心善,, 赵汉文, 王俊翔, 黄勇杰

Experimental study of dynamic elastic modulus and damping ratio of expansive soil in Hefei

ZHUANG Xin-shan,, ZHAO Han-wen, WANG Jun-xiang, HUANG Yong-jie

收稿日期: 2019-03-22  

Received: 2019-03-22  

作者简介 About authors

庄心善（1964—），男，教授，博导，从事环境岩土工程与边坡工程的研究.orcid.org/0000-0001-8319-8726.E-mail：zhuangxinshan@163.com , E-mail：zhuangxinshan@163.com

摘要

以合肥膨胀土为研究对象，利用GDS真动三轴仪对土体进行循环动荷载试验，研究不同围压、固结应力比对土体动弹性模量及阻尼比的影响规律.试验结果表明，合肥膨胀土的骨干曲线可以由双曲线描述；在相同条件下，动弹性模量随着围压、固结应力比的增大而增大，随着动应变的增大先急剧减小后趋于平缓；动弹性模量的倒数与动应变呈良好的线性关系，最大动弹性模量随着围压的增大呈线性增大，给出考虑围压影响的最大动弹性模量回归方程；阻尼比随着围压、固结应力比的增大而减小，采用 Darendeli 模型及依据阻尼比与应变的经验关系，得到动模量比衰减模型及阻尼比模型；不同围压、固结应力比下阻尼比与动模量比的关系归一化后可以由修正Hardin-Drnevich公式描述.

关键词： 膨胀土 ; 动三轴试验 ; 固结应力比 ; 动弹性模量 ; 阻尼比

Abstract

A series of dynamic triaxial tests were conducted by GDS to analyze the influence of different confining pressures, consolidation ratios on the dynamic modulus and damping ratio of the soil by taking expansive soil in Hefei as the research object. The test results show that the stress-strain backbone curve can be described by hyperbolic function. The dynamic modulus of elasticity increases with the increase of confining pressure and consolidation stress ratio, and decreases sharply at first then tends to be flat with the increase of dynamic strain under the same conditions. The reciprocal of elastic modulus has a linear relationship with dynamic strain. The maximum modulus increases linearly with the increase of confining pressure. A regression model of maximum dynamic modulus and elasticity regression considering confining pressure was developed. Damping ratio decreases with the increase of confining pressure and consolidation stress ratio. An attenuation model of dynamic modulus ratio and a damping ratio model were established based on the Darendeli’s model and empirical relation between damping ratio and strain. The relationship between damping ratio and dynamic modulus ratio under different confining pressure and consolidation stress ratio after normalization processing can be described by the modified formula of Hardin-Drnevich.

Keywords： expansive soil ; dynamic triaxial test ; consolidation stress ratio ; dynamic elastic modulus ; damping ratio

PDF (1414KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

庄心善, 赵汉文, 王俊翔, 黄勇杰. 合肥膨胀土动弹性模量与阻尼比试验研究. 浙江大学学报(工学版)[J], 2020, 54(4): 759-766 doi:10.3785/j.issn.1008-973X.2020.04.015

ZHUANG Xin-shan, ZHAO Han-wen, WANG Jun-xiang, HUANG Yong-jie. Experimental study of dynamic elastic modulus and damping ratio of expansive soil in Hefei. Journal of Zhejiang University(Engineering Science)[J], 2020, 54(4): 759-766 doi:10.3785/j.issn.1008-973X.2020.04.015

膨胀土是一种对水分敏感的高塑限黏性土，具有胀缩性、超固结性、多裂隙性，一般强度较高、压缩性低，在我国分布广泛. 近年来，我国高速公路及铁路等各类工程发展迅速，势必跨越更多的膨胀土地区. 随着车流量的快速增长、汽车速度及轴重提高，车辆荷载在路基中产生的动力响应问题已经成为土木工程领域中的研究热点[1-5].

目前，关于膨胀土的研究成果很多，但大多针对静力学方面[6-9]. 在膨胀土动力响应方面，李晶晶等[10]研究应力历史影响下的南阳膨胀土动力参数响应特征，分析应力历史对膨胀土动切变模量和阻尼比的影响规律；黄志全等[11]研究河北磁县膨胀土的动力特性变化规律，分析膨胀率对膨胀土动切变模量和阻尼比的影响规律；毛成等[12]研究成都膨胀土的动力特性，分析围压对膨胀土弹性应变和竖向累积应变的影响规律. 结果表明，由于地质年代、沉积环境的不同，不同地区膨胀土的结构构造存在一定差异，在动荷载下表现出的动力特性不同. 目前未见有关合肥膨胀土动力特性的研究成果报道.

关于土动力特性的影响因素有很多，主要包括动荷载幅值、循环荷载振动频率、围压、非饱和土含水率或饱和度、固结应力比、循环荷载振动次数和土体本身的结构性等[13-17]，其中围压和固结应力比是土体动力特性的2个主要影响因素. 本文利用 GDS真动三轴仪的动力加载模块，对膨胀土进行一系列循环动荷载试验，研究合肥膨胀土动应力-应变骨干曲线、动弹性模量、阻尼比变化规律. 比较分析围压、固结应力比对膨胀土动力特性的影响规律，建立动弹性模量比衰减模型及阻尼比归一化计算模型，为实际相关工程提供相关参考依据.

1. 土样制备与试验方案

1.1. 试验仪器和试验土样

试验仪器为英国GDS真动三轴仪，如图1所示，GDS 测量系统可以精准施加围压、轴向压力、反压，并实时记录土样的轴向应变、孔隙压力、体积应变等数据.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   GDS真动三轴试验仪及电子操控台

Fig.1   GDS dynamic triaxial test device and electronic console


试验土样取自于安徽合肥某高速公路工程. 土样的物理性质指标如表1所示. 表中，ρ为天然密度，W为含水率，W1为液限，Wp为塑限，Gs为比重，Fs为自由膨胀率. 按膨胀土自由膨胀率分级可以归类为弱膨胀土，通过击实试验得出土样最大干密度为1.75 g/cm3，最优含水率为17.5%. 按最优含水率和最大干密度制作重塑土样，试样直径为50 mm，高度为100 mm，制备时分5层捣实，每层进行刮毛处理.

表 1   合肥膨胀土基本物理力学参数

Tab.1  Basic physico-mechanical parameters of Hefei expansive soil

ρ/
(g·cm−3) 		W/% Wl /% Wp /% Gs Fs/%
1.9 21.64 72 30 2.68 44

新窗口打开| 下载CSV


1.2. 土样制备与试验方案

先将重塑试样放入饱和器内抽气饱和，再装入GDS真动三轴仪进行反压饱和，直至饱和度B达到 0.95时停止，最后施加设定的围压和轴向压力完成固结. 试验时，循环荷载波形采用正弦波，在不排水条件下分12级施加预设的动应力，每级循环振动 10 次. 当试样轴向应变达到5%时，视为破坏并终止试验[18].

动力加载试验考虑围压和固结应力比2个主要影响因素. 依据仇敏玉等[19]采用数值模型分析得到车辆荷载对路基的计算影响深度一般为6~10 m，该试验选取围压为100、150、200 kPa；考虑到天然状态下膨胀土土体多为偏压应力状态，该试验选取固结应力比kc为1.00、1.25、1.50，试验方案如表2所示. 表中，σ3为围压，σd为应力幅值.

表 2   膨胀土动力加载试验方案

Tab.2  Dynamic test scheme of expansive soil

组类 σ3/kPa kc σd/kPa
1 100 1.0，1.25，1.50 10～120
2 150 1.0，1.25，1.50 15～180
3 200 1.0，1.25，1.50 20～240

新窗口打开| 下载CSV


2. 试验结果及分析

2.1. 动应力-应变关系

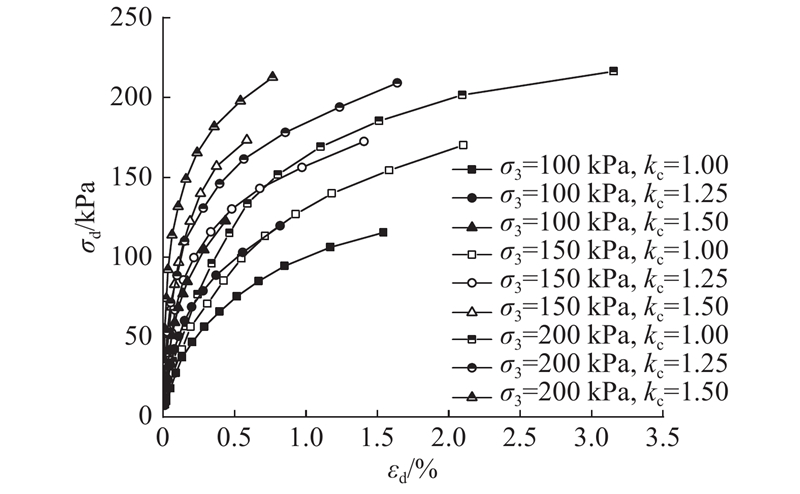
膨胀土试样的动应力σd-应变εd曲线如图2所示.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   膨胀土动应力-应变关系曲线

Fig.2   Relation curves of dynamic stress-strain of expansive soil


当εd<0.1%时，曲线较陡，随着动应力的增大，应变加速增大，曲线趋于平缓，呈现明显的非线性，整体呈双曲线关系. 在相同条件下，σd-εd曲线随着固结围压、固结应力比的增大而向上显著移动. 当初期εd<0.1%时土体处于弹性变形阶段，土体产生的变形主要为弹性变形，随着动应力幅值的增大，土体逐渐由弹性变形阶段过渡为塑性变形阶段，土体产生的变形以塑性变形为主导，应变发展加快；围压、固结应力比越大，相同应力幅值下土体的动应变越小，说明围压、固结应力比的增大能够抑制膨胀土动应变的发展.

2.2. 动弹性模量特性

动弹性模量Ed取滞回曲线两端点连线的斜率，即

${E_{\rm{d}}} = \frac{{{\sigma _{{\rm d}{\rm{max}}}}{\rm{ - }}{\sigma _{{\rm d}{\rm{min}}}}}}{{{\varepsilon _{{\rm d}{\rm{max}}}}{\rm{ - }}{\varepsilon _{{\rm d}{\rm{min}}}}}}.{\rm{ }}$

取每级荷载第 8~10 次循环加载的动弹性模量平均值和对应的平均动应变作为该级荷载的动弹性模量和动应变，绘制Ed-εd曲线,如图3、4所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

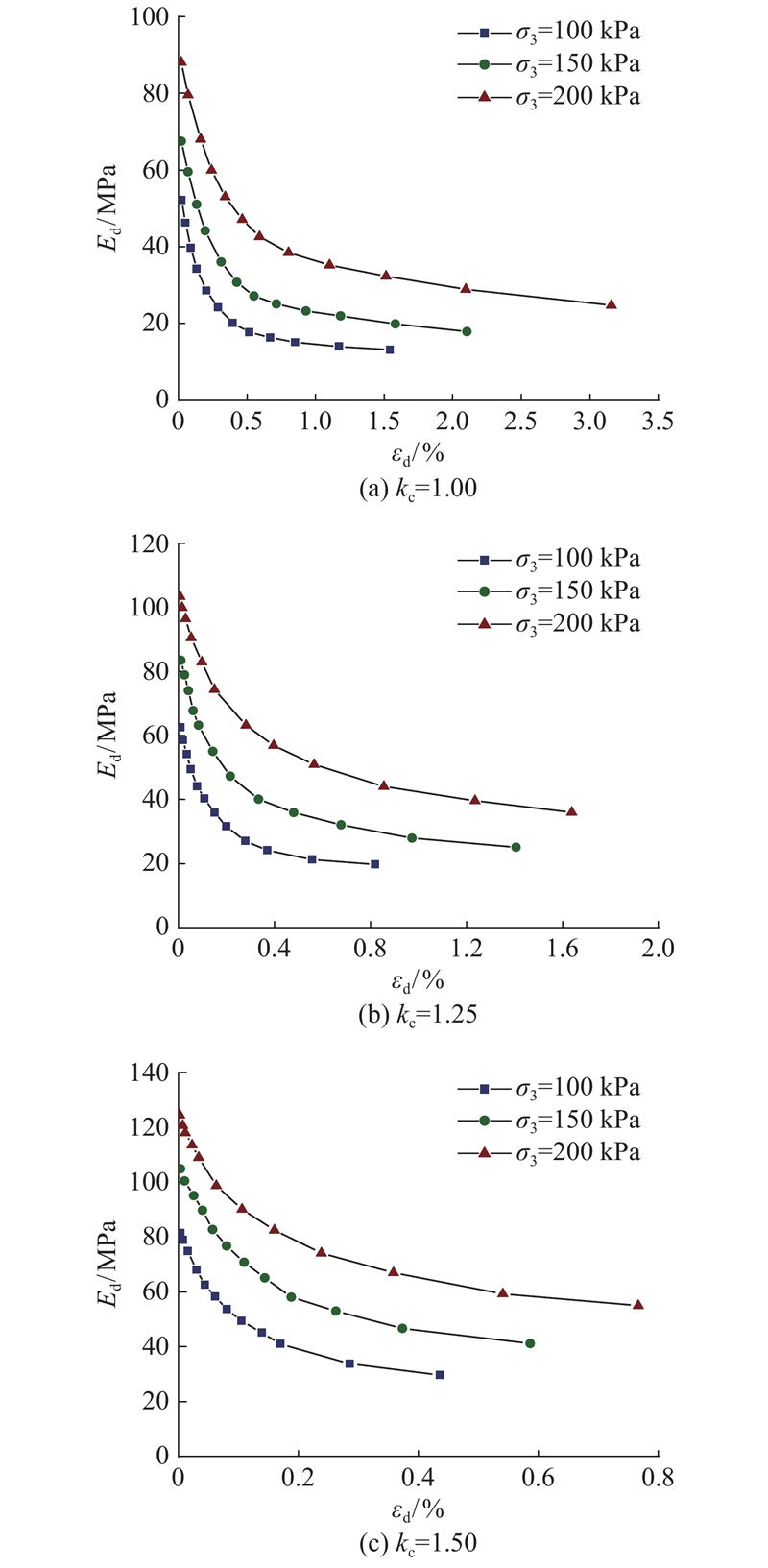
图 3   不同围压下膨胀土动弹性模量变化曲线

Fig.3   Dynamic elastic modulus-strain curves of expansive soil under different confining pressures


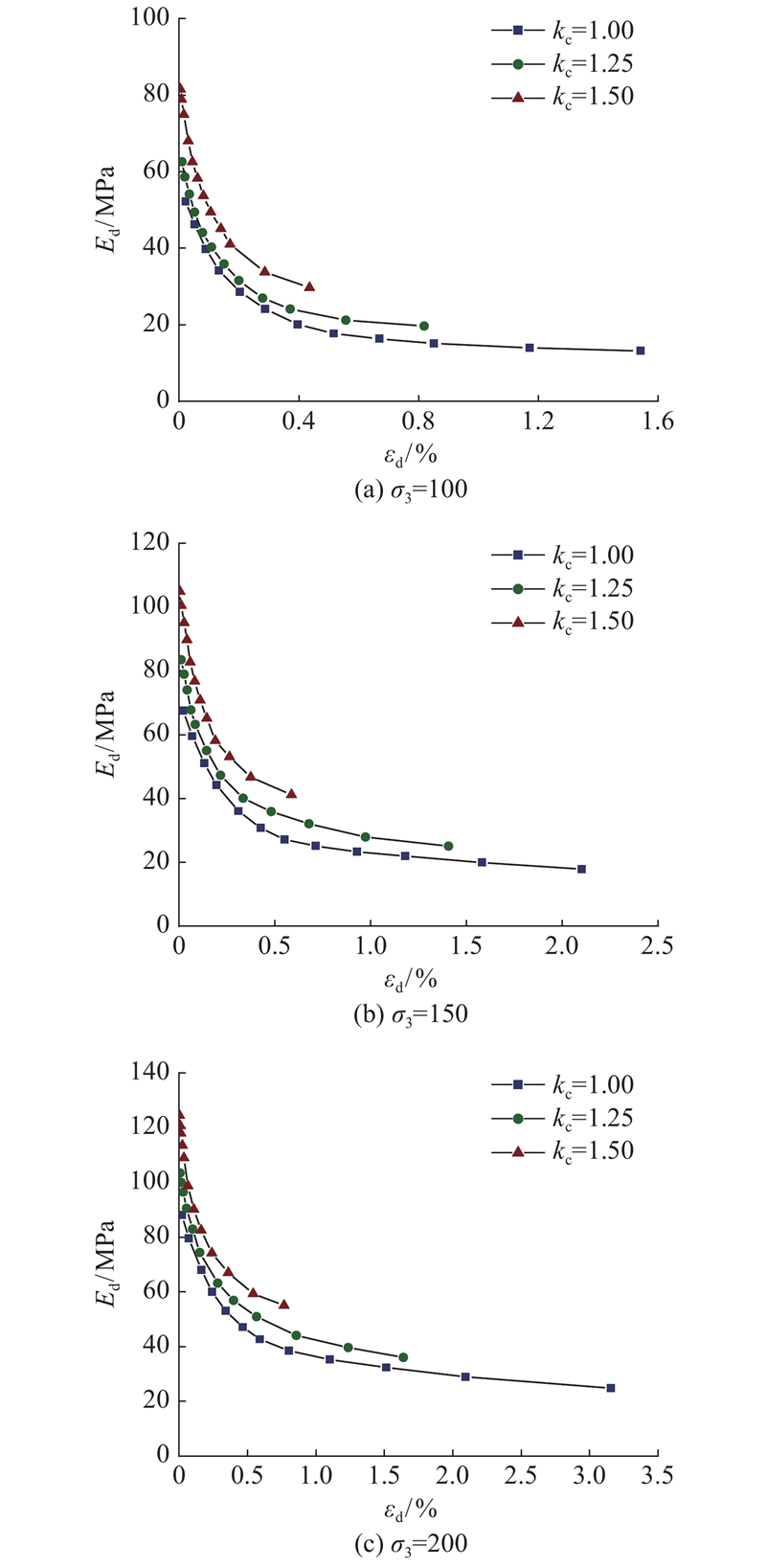
图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   不同固结应力比下膨胀土动弹性模量变化曲线

Fig.4   Dynamic elastic modulus-strain curves of expansive soil under different consolidation stress ratios


由图3、4可知，不同围压、固结应力比下膨胀土动弹性模量随着动应变的增大先急速减小后趋于平缓. 在应变初期，土体受到较小的动应力时能够充分回弹，塑性变形较小，初始动弹性模量较大，随着振级的增大，土体的塑性变形增大，导致弹性模量逐渐减小.

在相同条件下，Ed 随着围压、固结应力比的增大而增大，表现为 Ed-εd 曲线随着σ3、kc的增大而上移动. 随着围压、固结应力比的增大，土体受到的初始球应力增大，孔隙比变小，土颗粒之间的相互作用增强，相对滑移变得困难，土样抵抗变形的能力提高.

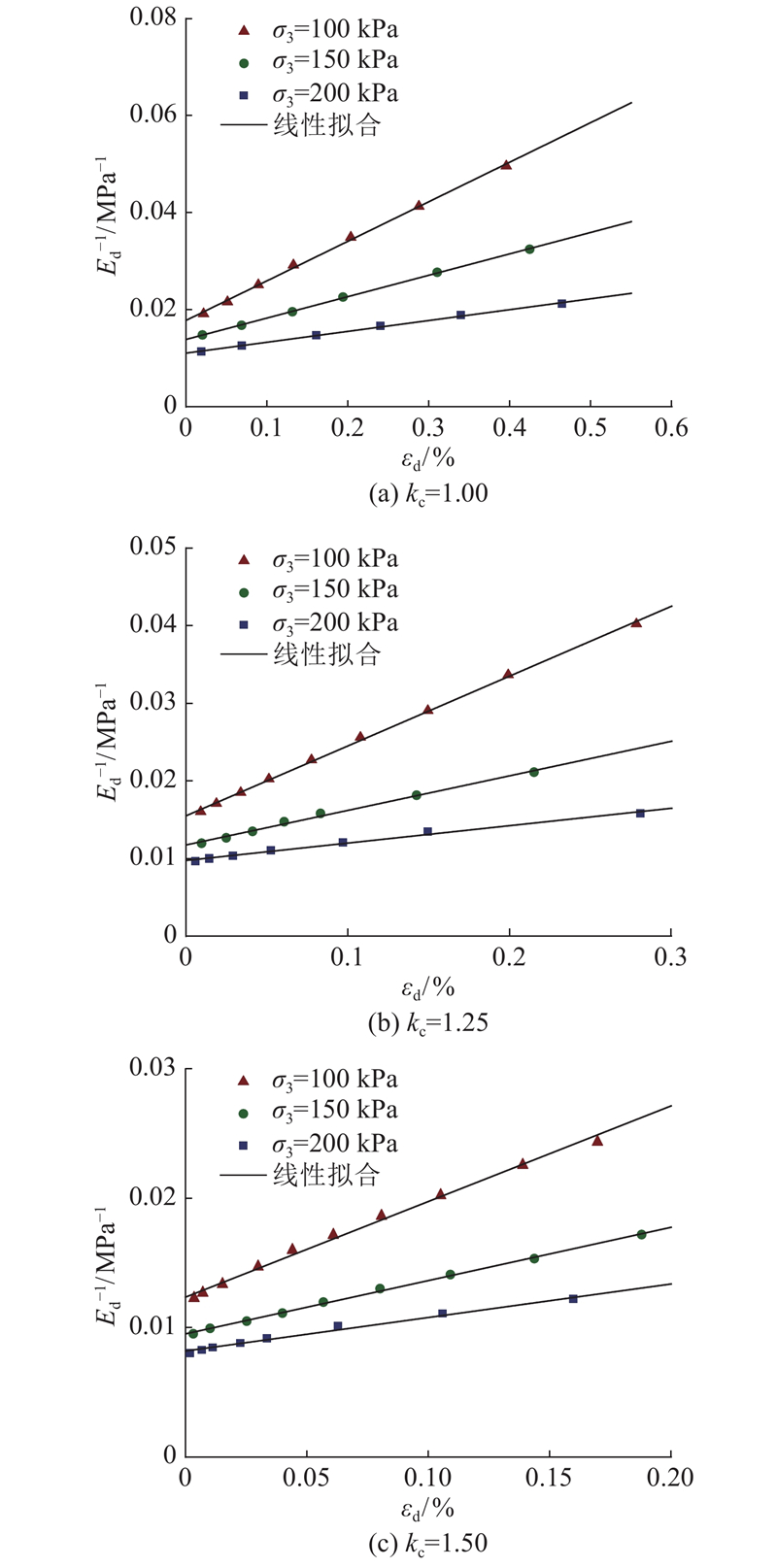
为了便于求最大动弹性模量Ed0，采用Kondner模型[20]:

${{\rm{1}}}/{{{E_{{\rm{d0}}}}}} = a{\rm{ }} + b{\varepsilon _{\rm{d}}}.{\rm{ }}$

式中： $a$、 $b$为拟合参数.

小应变幅值下1/Ed随εd的变化关系如图5所示. 由图5可知，1/Ed与εd的相关系数R 2均大于0.99，呈良好的线性关系，表明Kondner模型适用于研究小应变幅值下合肥膨胀土的Ed-εd关系.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   膨胀土动弹性模量倒数随动应变的变化关系

Fig.5   Relationships between reciprocal of dynamic elastic modulus with dynamic strains for expansive soil


直线在纵坐标上的截距为 $a$，斜率为 $b$，最大动弹性模量Ed0 由1/ $a$表示，可得Ed0随σ3、kc的变化特征，如图6、7所示.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

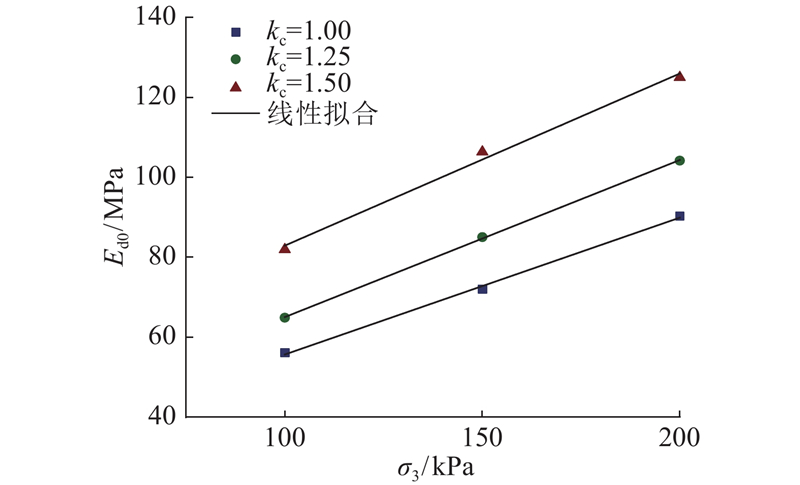
图 6   不同固结应力比下膨胀土最大动弹性模量随围压的变化关系

Fig.6   Relationships of Ed0 - σ3 for expansive soil under different consolidation stress ratios


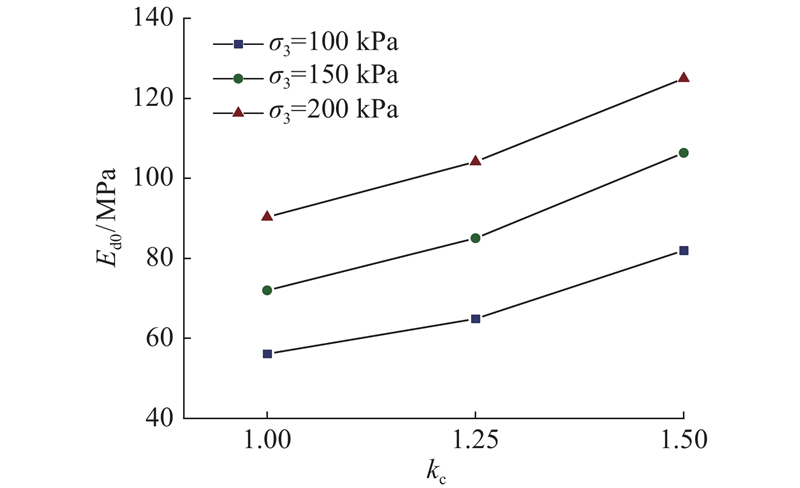
图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   不同围压下膨胀土最大动弹性模量随固结应力比的变化关系

Fig.7   Relationships of Ed0 - kc for expansive soil under different confining pressures


由图6、7可知，膨胀土的最大动弹性模量随着围压的增大呈线性增大，随着固结比的增大而增大，但线性关系不明显.

考虑围压的影响，建立Ed0的回归方程：

${E_{{\rm{d0}}}} = k{p_{\rm{a}}}{\left( {\frac{{{\sigma _3}}}{{{p_{\rm{a}}}}}} \right)^n}.{\rm{ }}$

式中：pa为大气压强, k 为图6中 σ3 =100 kPa 时Ed0与大气压的比值. 可得与围压有关的指数n为 0.61~0.67，R2=0.99.

2.3. 动模量比衰减模型

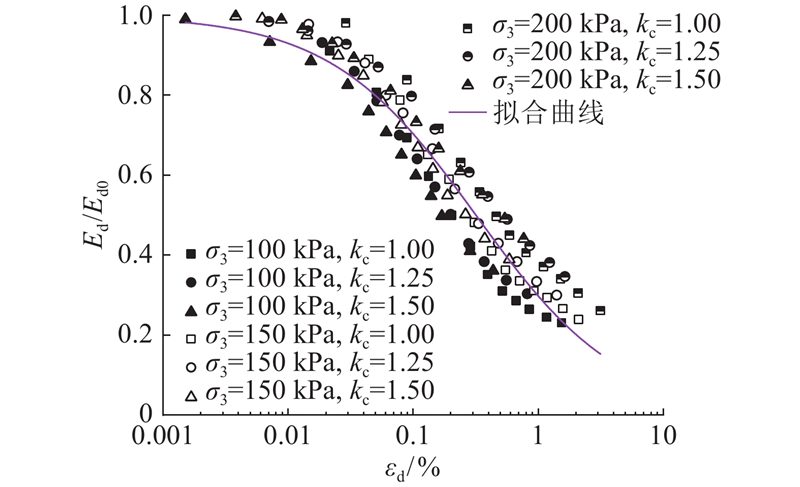
将不同试验条件下的Ed/Ed0-εd绘制在半对数坐标中，如图8所示.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   膨胀土动模量比随动应变的变化关系

Fig.8   Relationships of elastic modulus ratio with dynamic strains for expansive soil


由图8可知，在相同条件下，Ed/Ed0-εd随着围压的增大而向上移动，固结应力比对Ed/Ed0-εd的影响没有明显的倾向性.

目前，针对不同类型的土，专家学者推出众多动模量衰减模型，如Hardin-Drnevich 模型[21]、Davidenkov 模型[22]以及Darendeli模型[23] 等. 其中Darendeli模型考虑围压的影响，将广泛应用的Hardin-Drnevich 模型加以改进，即

$\frac{E_{\rm d}}{{{E_{{\rm{d}}0}}}} = \frac{1}{{1 + {{(c{\varepsilon _{\rm{d}}})}^d}}}.{\rm{ }}$

式中： $c$、 $d$为拟合参数. 利用Darendeli模型进行曲线拟合，可得合肥膨胀土动模量比衰减模型：

$\frac{E_{\rm d}}{{{E_{{\rm{d}}0}}}} = \frac{1}{{1 + {{(3.{\rm{152\;2}}{\varepsilon _{\rm{d}}})}^{0.7{\rm{46\;4}}}}}}.{\rm{ }}$

相关系数R2=0.926 1，能够较好地描述合肥膨胀土动弹性模量随动应变的变化规律.

2.4. 阻尼比变化规律

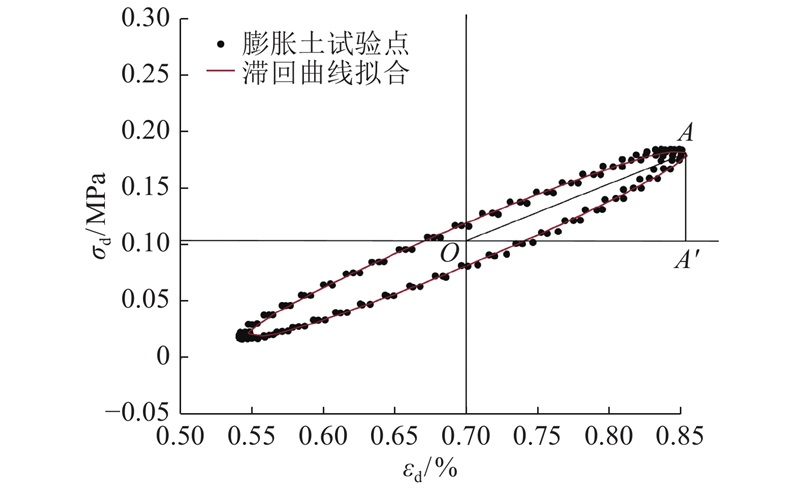
土的阻尼比λ反映了在循环动荷载作用下，部分能量因土体内阻尼而耗散的性质，表现为土动应力-应变滞回圈的滞后性，可以由土体在一个周期内损耗的能量 $\Delta W$与该循环中所储存总能量 $W$的比值表示[24]：

$ \lambda = \frac{1}{{4{\text{π}} }}\frac{{\Delta W}}{W}.{\rm{ }} $

如图9所示，在σ3=100 kPa，kc=1.00，第10级循环加载的条件下，取试样每级循环荷载中前3次加载的σd-εd试验点拟合出近似椭圆, $\Delta W$、 $W$可以由椭圆面积、三角形OAA'的面积表示：

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   膨胀土应力-应变滞回曲线

Fig.9   Stress-strain hysteresis curve of expansive soil


$ \lambda = \frac{1}{{4{\text{π}} }}\frac{{\text{椭圆面积}}}{{\text{三角形面积}}}. $

由于 $\lambda $随εd的变化规律较复杂，采用Hardin-Drnevich和Davidenkov 模型的拟合效果较差，采用式（8）[25]进行曲线拟合，结果如图10、11所示，参数如表3所示.

表 3   膨胀土阻尼比的拟合参数

Tab.3  Fitting parameters of damping ratio for expansive soil

kc σ3/kPa n m R2
1.00 100 0.242 1 1.667 9 0.994 9
1.00 150 0.318 8 1.636 1 0.996 0
1.00 200 0.407 0 1.475 8 0.996 7
1.25 100 0.208 0 1.954 1 0.992 1
1.25 150 0.263 6 1.763 4 0.995 6
1.25 200 0.294 9 1.832 2 0.997 9
1.50 100 0.160 9 2.766 5 0.990 1
1.50 150 0.192 9 2.472 5 0.989 8
1.50 200 0.232 9 2.461 0 0.992 9

新窗口打开| 下载CSV


图 10

新窗口打开| 下载原图ZIP| 生成PPT

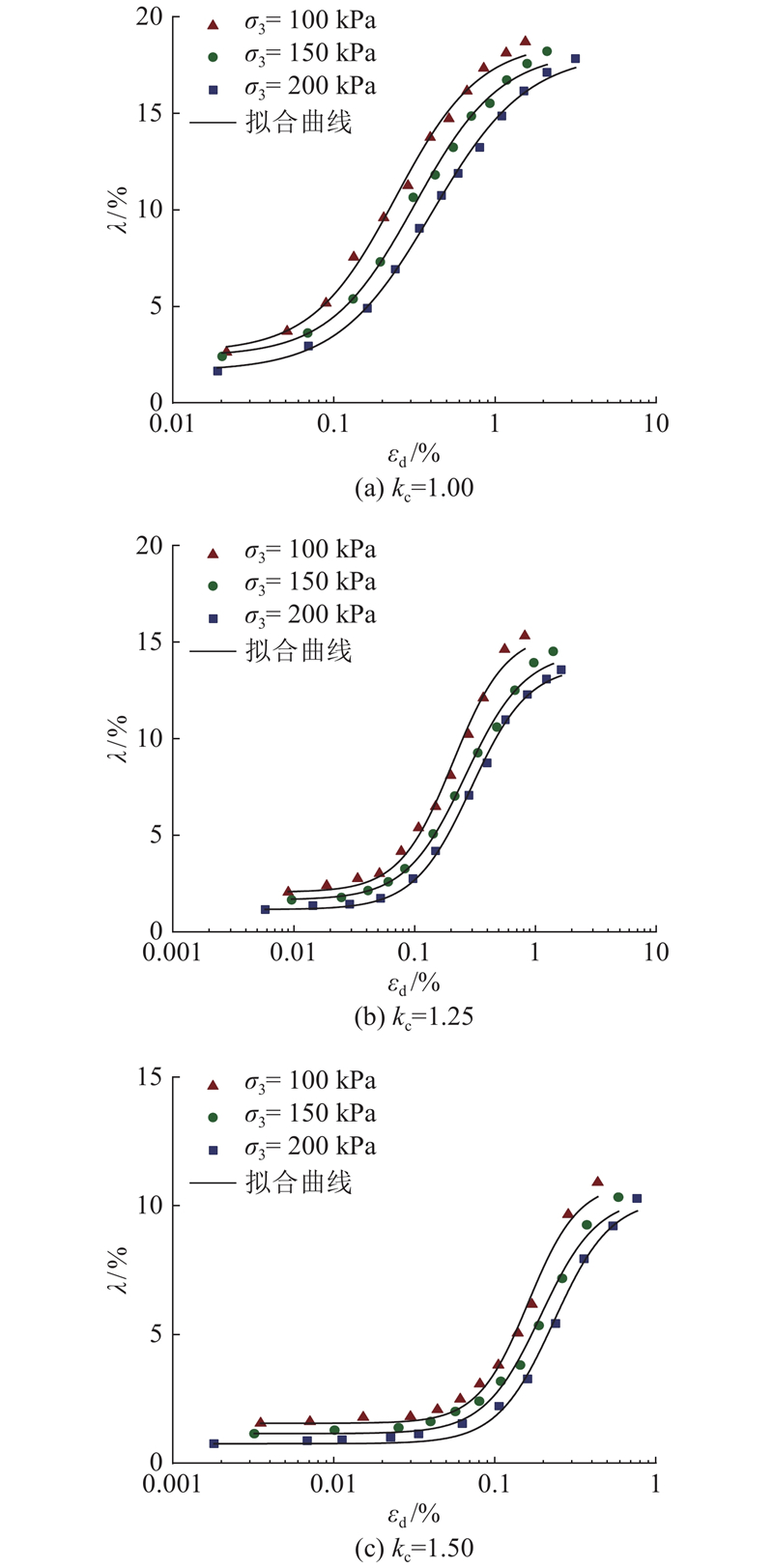
图 10   不同围压下膨胀土阻尼比随动应变的变化关系

Fig.10   Relationships of damping ratio with dynamic strain for expansive soil under different confining pressures


图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   不同固结应力比下阻尼比随动应变的变化关系

Fig.11   Relationships of damping ratio with dynamic strain under different consolidation stress ratios


$\lambda {\rm{ = }}{\lambda _{\max }} - \frac{{{\lambda _{\max }} - {\lambda _{\min }}}}{{1 + {{({\varepsilon _{\rm{d}}}{\rm{/}}n)}^m}}}.{\rm{ }}$

式中： $\lambda_{\rm{max}} $为最大阻尼比，由 $\lambda $-εd曲线增长至趋于平缓时的渐近线表示； $\lambda_{\rm{min}} $为最小阻尼比； $n$、 $m$为拟合参数.

由图10、11可知，膨胀土阻尼比随着动应变的增大而增大，在应变初期，增长较缓慢，随着εd的增大，增长速率加快. 说明试验前期加载的动应力较小，土体的刚度较大，土样对动荷载的反映更加及时，能量耗散较小；随着动应力的增大，土样产生了逐渐增大的塑性变形，刚度减小，能量损耗增大.

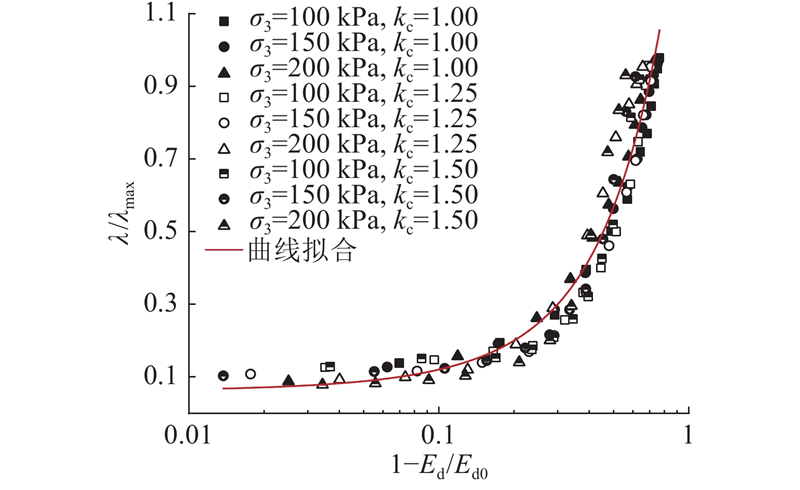
由图11可知，随着固结应力比的增大， $\lambda $-εd曲线整体向下移动，表明膨胀土对较高固结应力比下的动荷载反应更加及时. 竖向应力作用下颗粒之间更加紧密，提高了动荷载的传导效率，减少了能量损失.

绘制不同固结应力状态( $\lambda $/ $\lambda _{\rm{max}}$) 下与(1−Ed/Ed0) 的半对数曲线，如图12所示.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   膨胀土 $\lambda $/ $\lambda _{\rm{max}}$随1−Ed/Ed0的变化关系

Fig.12   Relationships between $\lambda $ / $\lambda _{\rm{max}}$ and 1−Ed/Ed0 of expansive soil


由图12可知，不同围压、固结应力比下的试验点交错分布在较窄范围内，可以近似归一化为一条曲线. 若采用Hardin-Drnevich公式进行拟合的结果偏差较大，采用修正Hardin-Drnevich公式进行拟合，结果如式（9），R2=0.940 1.

$\frac{\lambda }{{{\lambda _{\max }}}} = {\left(1 - \frac{{{E_{\rm{d}}}}}{{{E_{{\rm{d}}0}}}} + 0.261\;3\right)^{2.077\;4}}.{\rm{ }}$

3. 结　论

(1)合肥膨胀土的动弹性模量随着动应变的增大而减小，当动应变较小时，变化幅度较大，随着动应变的增大，变化幅度减小. 随着围压，固结应力比的增大，相同动应变下的动弹性模量增大.

(2)合肥膨胀土的最大动弹性模量随着围压和固结应力比的增大而增大，且与围压呈线性关系，通过分析试验数据得到相关指数为0.61~0.67.

(3) 利用Darendeli 模型描述合肥膨胀土的动模量衰减规律较好. 随着围压的增大，Ed/Ed0-εd曲线向上移动，固结应力比对Ed/Ed0-εd曲线的影响没有明显的倾向性.

(4)在相同条件下，随着围压、固结应力比的增大，膨胀土的阻尼比减小. ( $\lambda $ $/\lambda _{\rm{max}}$)与(1−Ed/Ed0)试验点交错在一条狭长的曲线内，固结应力比与围压对 $\lambda $ $\lambda _{\rm{max}}^{-1}$-(1−Ed/Ed0)关系的影响均不明显. 本文给出合肥膨胀土阻尼比增长规律的经验模型，归一效果良好.

参考文献

李明, 刘扬, 杨兴胜

考虑轴重相关的随机车流荷载效应

[J]. 浙江大学学报: 工学版, 2019, 53 (1): 78- 88

[本文引用: 1]

LI Ming, LIU Yang, YANG Xing-sheng

Random vehicle flow load effect considering axle load

[J]. Journal of Zhejiang University: Engineering Science, 2019, 53 (1): 78- 88

[本文引用: 1]

周小生. 双向循环荷载作用下膨胀土的动力特性与路基响应特征研究[D]. 北京: 中国科学院研究生院, 2010.

ZHOU Xiao-sheng. The dynamic characteristic of expansive soil and dynamic behaviors of subgrade under the bidirectional cyclic loading [D]. Beijing: Chinese Academy of Sciences, 2010.

曹海莹, 朱毅, 刘云飞, 等

车辆荷载作用下双层路基层间动应力响应试验研究

[J]. 振动与冲击, 2017, 36 (5): 30- 36

CAO Hai-ying, ZHU Yi, LIU Yun-fei, et al

Tests for interlayer dynamic stress response of a twolayer road-bed under vehicle load

[J]. Journal of Vibration and Shock, 2017, 36 (5): 30- 36

杨果林, 段君义, 杨啸, 等

降雨与自然状态下膨胀土基床的振动特性

[J]. 浙江大学学报: 工学版, 2016, 50 (12): 2319- 2327

YANG Guo-lin, DUAN Jun-yi, YANG Xiao, et al

Vibration characteristics of subgrade in expansive soil area under simulated rainfall and natural conditions

[J]. Journal of Zhejiang University: Engineering Science, 2016, 50 (12): 2319- 2327

PRIEST J A, POWRIE W

Determination of dynamic track modulus from measurement of track velocity during train passage

[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135 (11): 1732- 1740

DOI:10.1061/(ASCE)GT.1943-5606.0000130      [本文引用: 1]

肖杰, 杨和平, 林京松, 等

模拟干湿循环及含低围压条件的膨胀土三轴试验

[J]. 中国公路学报, 2019, 32 (1): 21- 28

DOI:10.3969/j.issn.1001-7372.2019.01.003      [本文引用: 1]

XIAO Jie, YANG He-ping, LING Jing-song, et al

Simulating wet-dry cycles and low confining pressures triaxial test on expansive soil

[J]. China Journal of Highway and Transport, 2019, 32 (1): 21- 28

DOI:10.3969/j.issn.1001-7372.2019.01.003      [本文引用: 1]

张锐, 张博亚, 郑健龙, 等

改进的膨胀土侧限膨胀试验研究

[J]. 岩土工程学报, 2018, 40 (12): 2223- 2230

ZHANG Rui, ZHANG Bo-ya, ZHENG Jian-long, et al

Modified lateral confined swelling tests on expansive soils

[J]. Chinese Journal of Geotechnical Engineering, 2018, 40 (12): 2223- 2230

戴福初, 董文萍, 黄志全, 等

南水北调中线段原状膨胀土抗剪强度试验研究

[J]. 工程科学与技术, 2018, 50 (6): 123- 131

DAI Fu-chu, DONG Wen-ping, HUANG Zhi-quan, et al

Study on shear strength of undisturbed expansive soil of middle route of south-to-north water diversion project

[J]. Advanced Engineering Sciences, 2018, 50 (6): 123- 131

杨和平, 唐咸远, 王兴正, 等

有荷干湿循环条件下不同膨胀土抗剪强度基本特性

[J]. 岩土力学, 2018, 39 (7): 2311- 2317

[本文引用: 1]

YANG He-ping, TANG Xian-yuan, WANG Xing-zheng, et al

Shear strength of expansive soils under wet-dry cycles with loading

[J]. Rock and Soil Mechanics, 2018, 39 (7): 2311- 2317

[本文引用: 1]

李晶晶, 孔令伟

应力历史影响下的膨胀土动力参数响应特征

[J]. 振动与冲击, 2017, 36 (12): 181- 188

[本文引用: 1]

LI Jing-jing, KONG Ling-wei

The influence of stress history on the dynamic parameters of expansive soils

[J]. Journal of Vibration and Shock, 2017, 36 (12): 181- 188

[本文引用: 1]

黄志全, 张茜, 吴超, 等

膨胀土动力学特性变化规律试验研究

[J]. 华北水利水电大学学报: 自然科学版, 2016, 37 (2): 78- 82

[本文引用: 1]

HUANG Zhi-quan, ZHANG Qian, WU Chao, et al

Experimental study on the variational regularity of dynamic characteristics of expansive soil

[J]. Journal of North China University of Water Resources and Electric Power: Natural Science Edition, 2016, 37 (2): 78- 82

[本文引用: 1]

毛成, 邱延峻

膨胀土与改性膨胀土的动力特性试验研究

[J]. 岩石力学与工程学报, 2005, (10): 1783- 1788

DOI:10.3321/j.issn:1000-6915.2005.10.025      [本文引用: 1]

MAO Cheng, QIU Yan-jun

Testing study on dynamic properties of expansive soil and improved expansive soil

[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, (10): 1783- 1788

DOI:10.3321/j.issn:1000-6915.2005.10.025      [本文引用: 1]

刘干斌, 谢琦峰, 高京生, 等

动荷载作用下重塑黏质粉土的弹性变形研究

[J]. 振动与冲击, 2018, 37 (10): 255- 260

[本文引用: 1]

LIU Gan-bin, XIE Qi-feng, GAO Jing-sheng, et al

Dynamic characteristics of saturated remolded clayey silt

[J]. Journal of Vibration and Shock, 2018, 37 (10): 255- 260

[本文引用: 1]

丁祖德, 黄娟, 袁铁映, 等

昆明泥炭质土动剪切模量与阻尼比的试验研究

[J]. 岩土力学, 2017, 38 (12): 3627- 3634

DING Zu-de, HUANG Juan, YUAN Tie-ying, et al

Experimental study of dynamic shear modulus and damping ratio of peaty soil in Kunming

[J]. Rock and Soil Mechanics, 2017, 38 (12): 3627- 3634

高洪梅, 沈艳青, 王志华, 等

EPS混合土的动模量和阻尼比特性

[J]. 岩土工程学报, 2017, 39 (2): 279- 286

DOI:10.11779/CJGE201702011     

GAO Hong-mei, SHEN Yan-qing, WANG Zhi-hua, et al

Dynamic modulus and damping ratio characteristics of EPS composite soil

[J]. Chinese Journal of Geotechnical Engineering, 2017, 39 (2): 279- 286

DOI:10.11779/CJGE201702011     

张泽林, 吴树仁, 唐辉明, 等

黄土和泥岩的动力学特性及微观损伤效应

[J]. 岩石力学与工程学报, 2017, 36 (5): 1256- 1268

ZHANG Ze-lin, WU Shu-ren, TANG Hui-ming, et al

Dynamic characteristics and microcosmic damage effect of loess and mudstone

[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36 (5): 1256- 1268

孔令伟, 臧濛, 郭爱国

湛江黏土动剪切模量的结构损伤效应与定量表征

[J]. 岩土工程学报, 2017, 39 (12): 2149- 2157

DOI:10.11779/CJGE201712001      [本文引用: 1]

KONG Ling-wei, ZANG Meng, GUO Ai-guo

Structural damage effect on dynamic shear modulus of Zhanjiang clay and quantitative characterization

[J]. Chinese Journal of Geotechnical Engineering, 2017, 39 (12): 2149- 2157

DOI:10.11779/CJGE201712001      [本文引用: 1]

SEED H B, LEE K L

Liquefaction of saturated sand during cyclic loading

[J]. Journal of the Soil Mechanics and Foundation Division, ASCE, 1966, 92 (SM6): 105- 134

[本文引用: 1]

仇敏玉, 俞亚南

道路行车荷载影响深度分析

[J]. 岩土力学, 2010, 31 (6): 1822- 1826

DOI:10.3969/j.issn.1000-7598.2010.06.025      [本文引用: 1]

QIU Min-yu, YU Ya-nan

Analysis of influence depth for roads induced by vehicle load

[J]. Rock and Soil Mechanics, 2010, 31 (6): 1822- 1826

DOI:10.3969/j.issn.1000-7598.2010.06.025      [本文引用: 1]

KONDNER R L

Hyperbolic stress-strain responses: cohesive soil

[J]. Journal of the Soil Mechanics and Foundation Division, ASCE, 1963, 89 (1): 115- 143

[本文引用: 1]

HARDIN B O, DRNEVICH V P

Shear modulus and damping in soils: measurement and parameter effect

[J]. Journal of Soil Mechanics and Foundations Division, 1972, 98 (SM6): 603- 624

[本文引用: 1]

ROLLINS K M, EVANS M D, DIEHL N B, et al

Shear modulus and damping relationships for gravels

[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124 (5): 396- 405

DOI:10.1061/(ASCE)1090-0241(1998)124:5(396)      [本文引用: 1]

DARENDELI M B. Development of a new family of normalized moduli reduction and material damping curves [D]. Austin: University of Texas at Austin, 2001.

[本文引用: 1]

谢定义. 土动力学[M]. 北京: 高等教育出版社, 2011: 148.

[本文引用: 1]

齐剑峰. 饱和黏土循环剪切特性与软化变形的研究[D]. 大连: 大连理工大学, 2007.

[本文引用: 1]

QI Jian-feng. A study on cyclic shear behavior and softening deformation of saturated clay [D]. Dalian: Dalian University of Technology, 2007.

[本文引用: 1]

/

〈 〉