目前,针对水平荷载作用下等径桩桩身内力及变形分布特征的研究已经比较完备[10-12]. Zhang等[3]基于线弹性地基反力法,得到多层土中桩基的水平内力响应的半解析解. 为了计算嵌入多层弹性土中水平受荷桩群的内力响应,Tehrani等[13] 运用变分原理和总势能最小原理,得到多层土体中群桩位移分布的半解析解. 为了进一步分析阶梯形变截面桩的水平承载特性,国内外学者展开了室内模型试验与现场试验研究. Ismael等[1]在科威特通过现场测试,研究6根不同变径位置的阶梯形钻孔桩、8根等径钻孔桩在砂土中的内力响应. 结果表明,扩大桩上段直径可以增强水平承载能力,当扩径直径超过其长度的40%时,阶梯形桩的承载力保持不变.
为了全面地分析阶梯形变截面桩在水平荷载作用下的内力及变形分布特征,本文基于线弹性地基反力法,提出水平荷载作用下多级阶梯形变截面桩内力与变形的简化解析算法. 编制MATLAB程序,分析长径比、变径位置以及桩径比等几何参数对桩身水平承载特性的影响效应. 将本文的预测结果与现场实测结果进行对比分析,验证了该算法的可行性,为变截面桩的工程设计提供了可靠依据.
1. 水平受荷阶梯形变截面桩计算方法
1.1. 多级阶梯形变截面桩挠曲微分方程
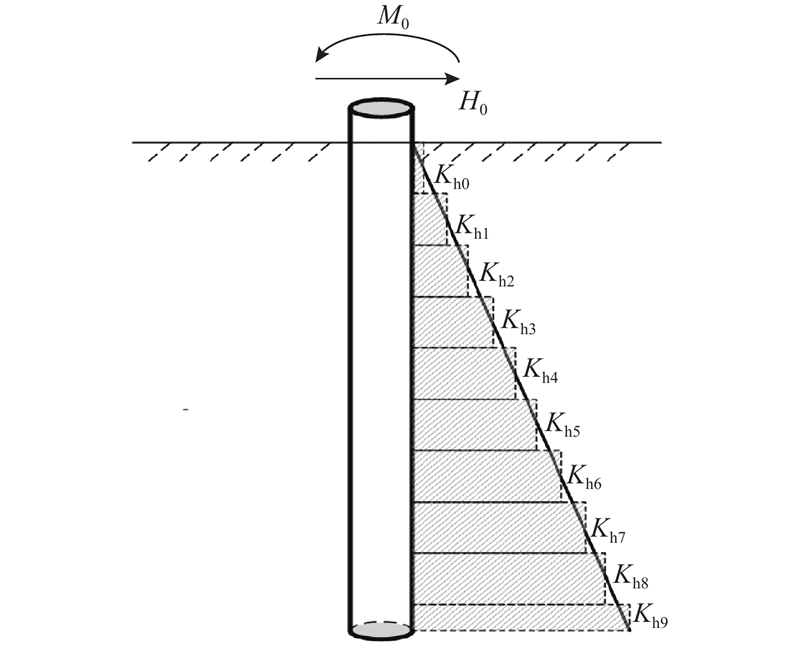
在桩顶水平荷载Ht和弯矩Rt 的共同作用下,如图1所示,m级阶梯形变截面桩桩底位移为Xb,转角为
图 1
为了便于分析,作出如下假设.
1)土体处于弹性变形范围内,桩侧任一点的土抗力与桩身侧向挠曲呈线性关系.
2)变截面处土体提供的抵抗弯矩很小,可以忽略不计.
为了便于描述全桩整体变形与桩段局部变形之间的关系,以桩顶中心(标记为O)为原点建立整体笛卡尔坐标系x-z,以各桩段顶部中心为桩段原点建立局部笛卡尔坐标系xi-zi. 桩身总长等于各桩段长度之和,即
式中:
式中:
式(2)所示微分方程的通解可以表示为
式中:
式中:
将式(3)、(5)合并,可得
式中:
针对等截面桩,如果桩侧土体为均质土层,只需根据桩端边界条件求解桩身挠曲微分方程,可以得到桩身内力与变形分布. 若桩周分布有多层土体,则需根据桩周土体的分层情况将桩身进行分段,引入相邻桩段间的连续性条件以及桩端边界条件,利用矩阵传递法求解桩身挠曲微分方程.
每个桩段的边界条件可以表示为
式中:
全桩整体边界条件为
将式(7)第1式代入式(8),可得
式中:
将式(11)代入式(7),可得
式中:
为了根据已知的整体边界条件
式中:
将式(13)代入式(9)的最后两式,可得以下迭代关系:
式中:
将式(13)代入式(9)中前2个连续条件,引入式(16)可得以下迭代关系:
式中:矩阵
经化简后,式(19)可以写成以下形式:
式中:
由式(17)、(20),可得
式中:
根据式(22)可知,
式中:
其中
根据式(10)、(24)给出的
式中:
将式(26)进行调整,可以得到X1和Φ1的表达式:
因此
式中:
式中:
式中:
1.2. 边界条件
桩顶自由:
桩端嵌固:
若桩顶弯矩、剪力以及桩底位移、转角未知,桩顶位移、转角以及桩底弯矩、剪力已知,根据式(31)可得整体8个边界条件的线性关系:
式中:
根据式(35),可以解得需要的4个边界条件Xb、Φb、Rt、Ht.
1.3. 算法流程
为了计算表征水平受荷单桩响应的参数,计算过程如下.
1)根据桩段或土层将桩身细分.
2)为了计算由式(30)给出的矩阵M,首先应该得到矩阵U[n],这需要根据式(18)、(21)进行一次从第一个桩段到最后一个桩段的迭代计算. 在该过程中,获得的每个桩段的U[i]将在后面的计算中应用.
3)当边界条件不是G[0]时,首先应该计算矩阵V,根据式(35)得到Xt、Φt、Rb、Hb. 然后根据式(29)获得第一桩段的边界条件G[1];获得矩阵F[i]. 引入得到的矩阵U[i],根据式(24)可得每个桩段的边界条件G[i]. 此外,将G[i]代入式(13),可得矩阵F[i],从而得到桩身的内力及变形.
利用MATLAB对水平荷载作用下多层土体中阶梯形变截面桩内力及变形分布进行编程,具体的实现流程如图2所示.
图 2
图 2 水平受荷阶梯形变截面桩内力响应计算流程图
Fig.2 Calculation flow chart for response of horizontally loaded step-tapered piles
2. 实例验证
为了验证该算法的正确性,将本文预测结果分别与已有数据进行对比,具体分析如以下2个案例.
2.1. 与等径桩的结果对比
式中:
图 3
图 4
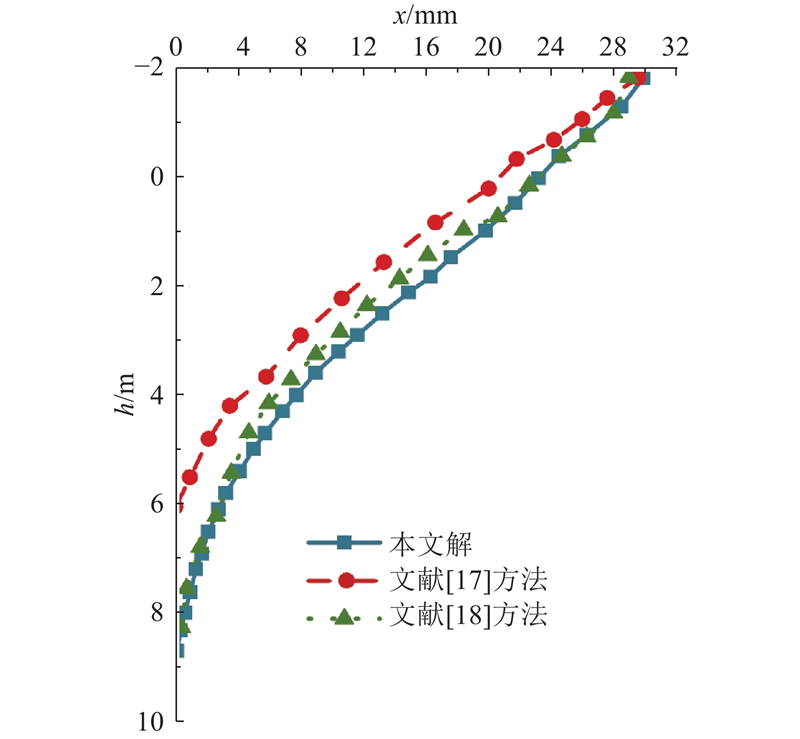
图 4 桩身位移计算值与数值结果、实测结果的对比
Fig.4 Computed horizontal displacement contrast with numerical results and field test results
图 5
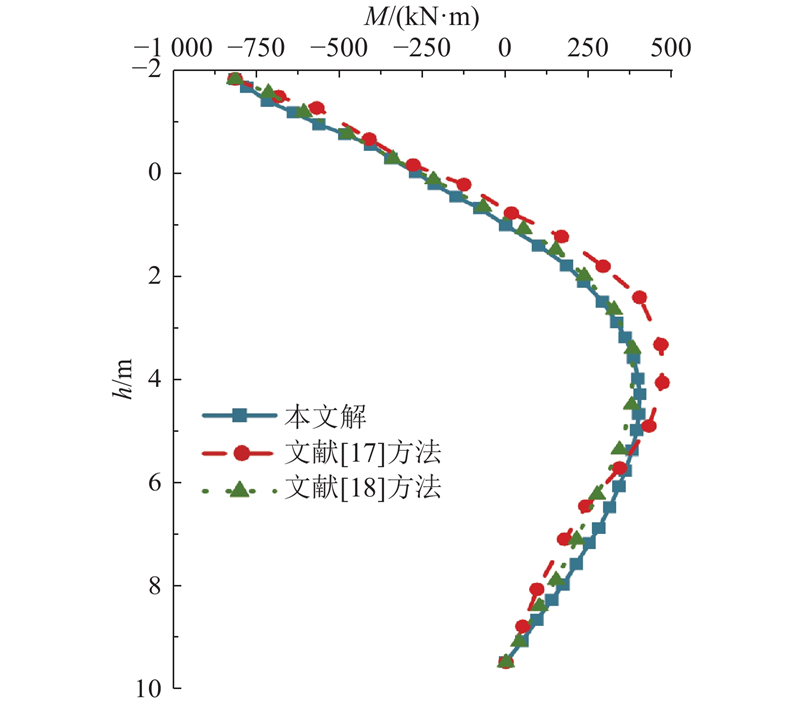
图 5 桩身弯矩计算值与数值结果、实测结果的对比
Fig.5 Computed bending moment contrast with numerical results and measurement results
2.2. 与变截面桩的结果对比
| 土体类别 | t/m | v | Es /kPa | Esoil /kPa |
| 中密砂 | 4 | 0.3 | 22 900 | 17 011.3 |
| 粉砂 | 1 | 0.3 | 29 840 | 22 166.86 |
图 6
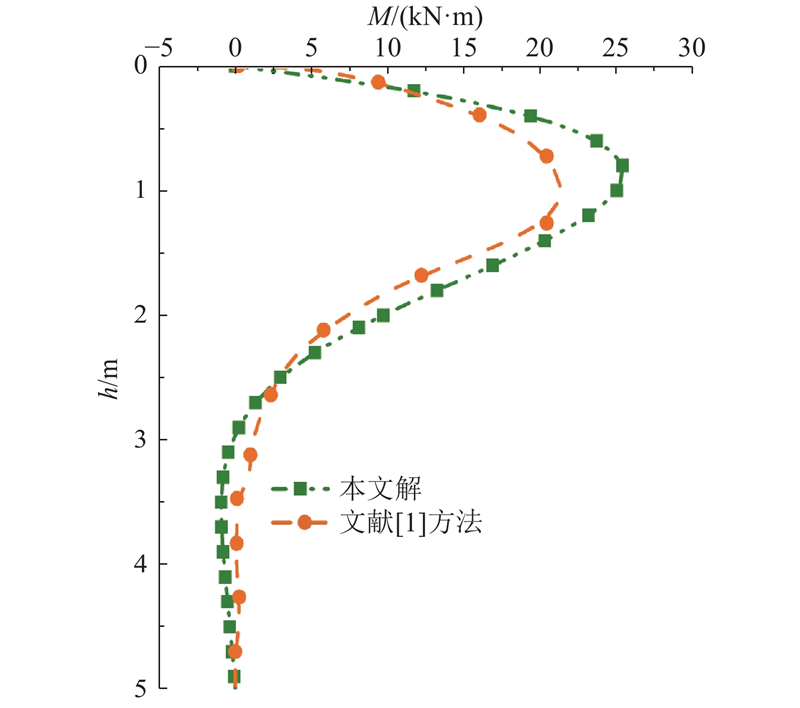
图 6 桩身弯矩计算值与现场实测结果的对比
Fig.6 Computed bending moment contrast with numerical results and field test results
3. 桩身几何参数影响效应分析
为了探讨水平向荷载作用下阶梯形变截面桩桩-土相互作用机理,基于本文算法,分别讨论桩身长径比(桩长与最大直径的比值)、变径位置(直径扩大段长度占总桩长的比例)以及桩径比(桩底直径与桩顶直径的比值)对水平向荷载作用下阶梯形变截面桩的桩身位移、桩身弯矩分布规律的影响. 具体参数选取如下:桩顶水平荷载H为100 kN,桩身总长h为10 m,Ep为25 GPa,土体水平反力模量k为20 MPa. 不同工况下的桩身参数如表2所示. 表中,L为长度,D为桩顶直径,d为桩底直径。
表 2 不同工况下的桩身参数
Tab.2
| L/D | D | d | d/D | 变径位置 |
| 10 | 1 | 0.6 | 0.6 | 40% |
| 12 | 0.83 | 0.5 | 0.6 | 40% |
| 14 | 0.7 | 0.42 | 0.6 | 40% |
| 16 | 0.625 | 0.375 | 0.6 | 40% |
| 18 | 0.55 | 0.33 | 0.6 | 40% |
| 20 | 0.5 | 0.3 | 0.6 | 40% |
| 20 | 0.5 | 0.3 | 0.6 | 20% |
| 20 | 0.5 | 0.3 | 0.6 | 40% |
| 20 | 0.5 | 0.3 | 0.6 | 60% |
| 20 | 0.5 | 0.3 | 0.6 | 80% |
| 20 | 0.5 | 0.25 | 0.5 | 40% |
| 20 | 0.5 | 0.3 | 0.6 | 40% |
| 20 | 0.5 | 0.35 | 0.7 | 40% |
| 20 | 0.5 | 0.4 | 0.8 | 40% |
| 20 | 0.5 | 0.45 | 0.9 | 40% |
| 20 | 0.5 | 0.5 | 1.0 | 40% |
3.1. 长径比的影响
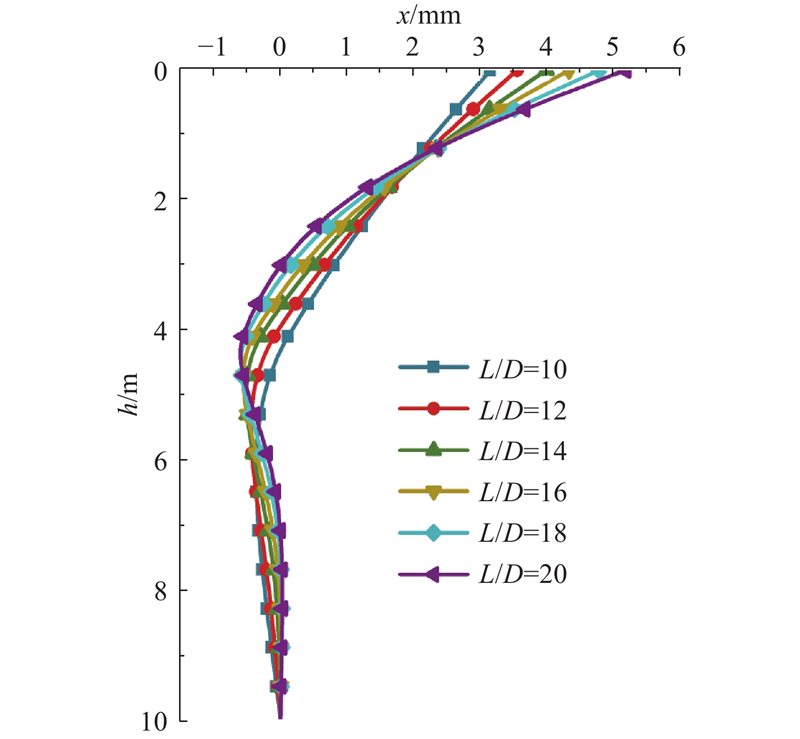
分析长径比对水平受荷阶梯形变截面桩位移及弯矩分布的影响效应. 假定桩径比为0.6,变径位置为40%(即大直径段的长度为4 m,小直径段的长度为6 m). 如图7所示为长径比对阶梯形变截面桩位移分布的影响. 可见,桩身变形主要集中在大直径段,且水平位移沿深度呈非线性减小;长径比为10、12、14、16、18、20对应的桩顶水平位移分别为3.14、3.54、3.98、4.32、4.77、5.12 mm. 可见,桩顶位移随着长径比的增大而逐步增大,位移反弯点逐步向桩顶靠近.
图 7
长径比对桩身弯矩分布的影响如图8所示. 增大长径比使得桩身弯矩峰值呈依次递减的趋势,但减小的幅度会逐渐降低,弯矩峰值点与反弯点所在位置均向桩顶移动. 由此可见,当桩顶位水平位移在桩身位移容许值内时,适当地增大桩身长径比有利于减小桩身弯矩. 对于细长桩(长径比更大),桩身的截面惯性矩更小,因此,水平荷载将更多由土体承担以至发生更大的水平位移,这一规律与等径桩类似.
图 8
3.2. 变径位置的影响
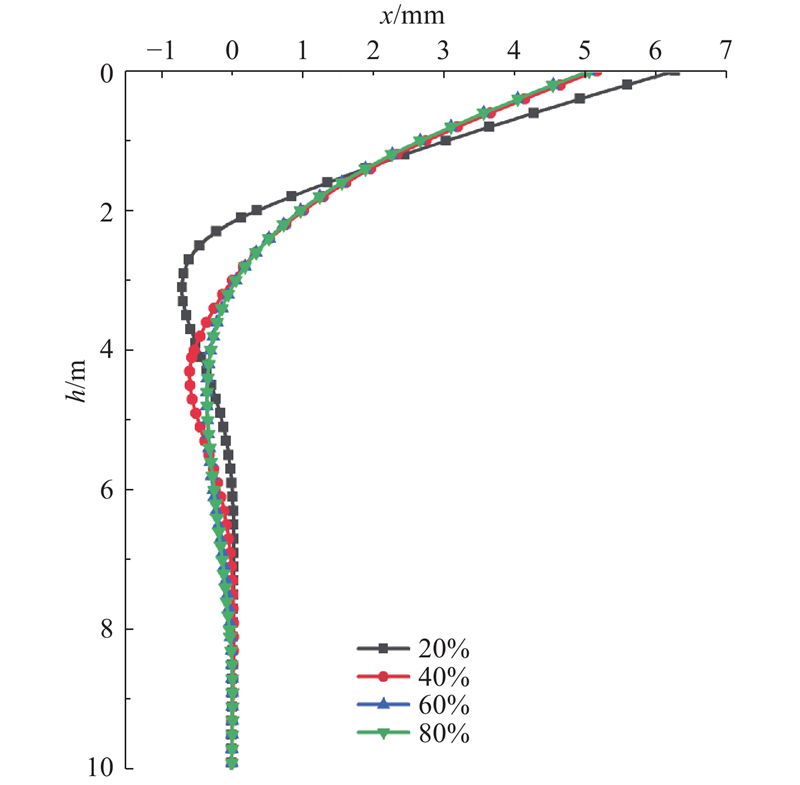
Ismael[1]通过现场试验研究变径位置对阶梯形变截面桩水平极限荷载的影响,得到最优变径位置为40%. 为了在理论上分析变径位置对水平荷载作用下阶梯形变截面桩桩身位移与弯矩分布的影响,假定长径比为20,桩径比为0.6,即桩顶直径为0.5 m,桩底直径为0.3 m. 如图9所示为变径位置对阶梯形变截面桩位移分布的影响图. 可以看出,变径位置为20%、40%、60%、80%所对应的桩顶最大水平位移依次为6.27、5.16、5.06、5.05 mm. 由此可知,变径位置下移有利于减小桩身最大水平位移,提高阶梯形变截面桩水平承载能力,然而随着变径位置的下移,位移变化幅度呈降低的趋势,在变径位置下降至40%后,继续下移变径位置对桩身最大水平位移的影响很小. 当上部扩大直径段长度所占比例超过40%时,对提高桩身水平承载能力无显著效果,该结论与通过现场试验得到的结果较一致.
图 9
图 9 变径位置对桩身位移分布的影响
Fig.9 Influence of location of discontinuity in diameter on displacement
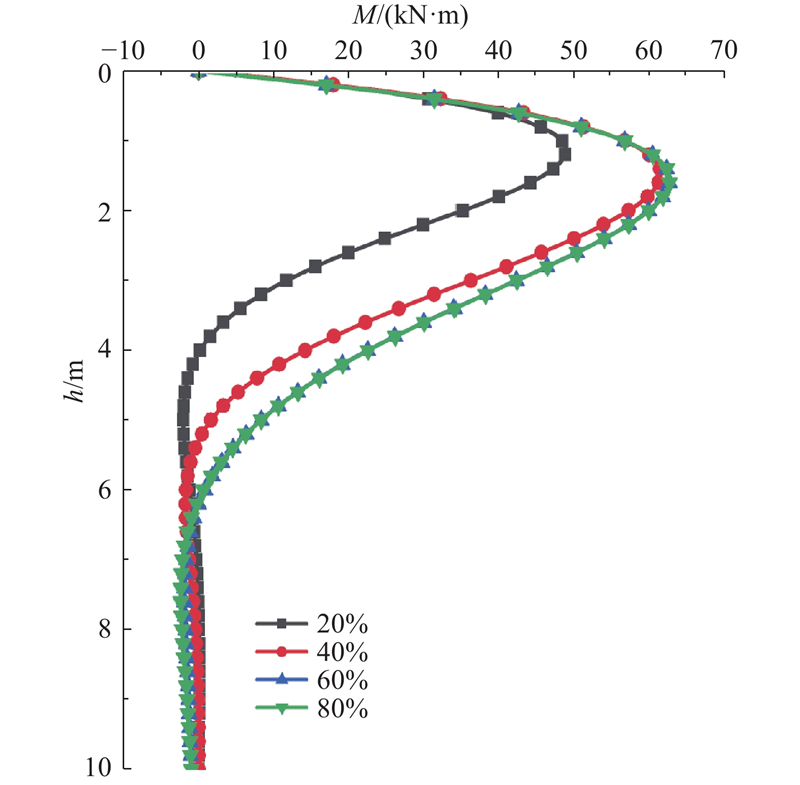
变径位置对变截面桩弯矩分布的影响如图10所示. 在水平荷载作用下,桩身弯矩自桩顶至桩底呈先增大后减小的趋势. 在桩-土共同作用过程中,浅层土体提供的水平抗力较小,但挤压变形较大;当桩侧土层水平抗力增大至与水平荷载相等时,弯矩达到最大值. 在变径位置向桩底移动的过程中,桩身弯矩峰值点的位置存在下移的趋势. 弯矩峰值点位置即为桩身最薄弱位置,在桩身结构设计时,应尽量使最大弯矩出现在大直径段. 综上所述,该算法未考虑土体的塑性变形,仅适用于桩身发生小变形的情况,未能得到桩身的水平极限荷载,后续展开关于水平荷载作用下阶梯形变截面桩的非线性分析方面的研究.
图 10
图 10 变径位置对桩身弯矩分布的影响
Fig.10 Influence of location of discontinuity in diameter on moment
3.3. 桩径比的影响
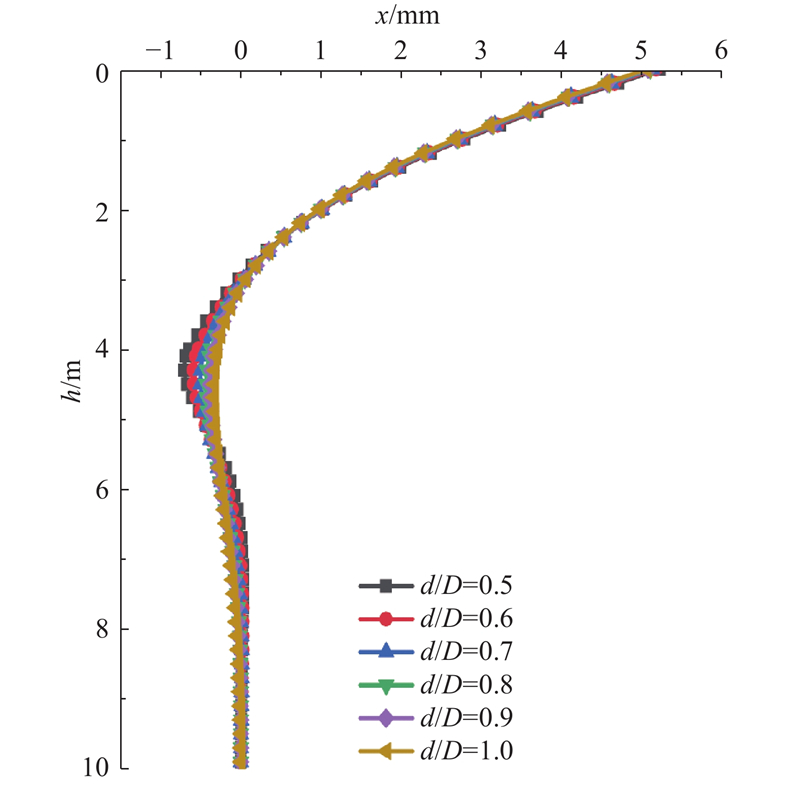
为了分析桩径比对桩身位移与弯矩分布的影响,桩顶直径保持恒定,仅改变桩底直径,假定桩身长径比为20,变径位置为40%,桩径比对阶梯形变截面桩位移分布的影响如图11所示. 可以看出,随着桩径比的增大,即扩大桩底直径,桩身抗弯刚度增加,最大水平位移略有减小.
图 11
图 11 桩径比对桩身位移分布的影响
Fig.11 Influence of butt diameter to tip diameter on displacement
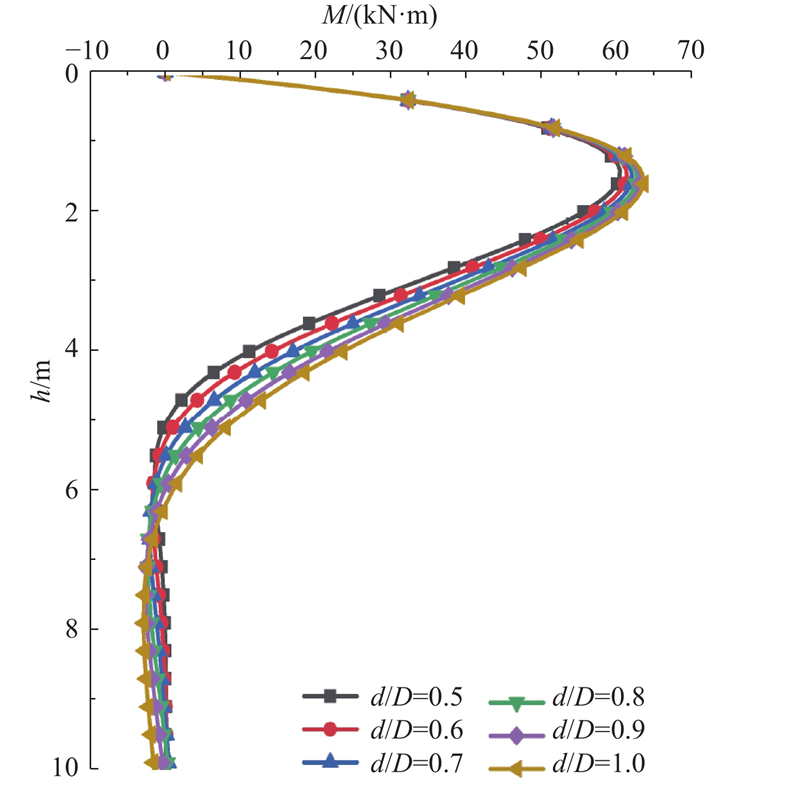
不同桩径比的弯矩分布如图12所示,弯矩最大值均位于大直径段,扩大桩径比使得桩身弯矩峰值增大,峰值点所处深度略向桩底靠近. 可以看出,与等径桩(d/D=1)相比,当桩顶位移未超过桩身容许位移时,适当减小下部桩径形成阶梯形变截面桩,有利于减小桩身弯矩峰值,且桩身下部小直径段出现负弯矩,可以有效地避免应力集中.
图 12
图 12 桩径比对桩身弯矩分布的影响
Fig.12 Influence of butt diameter to tip diameter on moment
4. 结 论
(1)基于线弹性地基反力法,假定相同土层的地基反力模量为常数(适用于超固结黏性土和表面密实的砂土),引入阶梯形变截面桩相邻两层之间的变形协调以及桩顶桩端边界条件,得到水平荷载作用下多级阶梯形变截面桩的内力及变形算法. 通过与Ismael[1]的现场实测结果对比发现,该方法可以反映水平受荷阶梯形变截面桩的内力及变形特征.
(2)基于提出的关于水平受荷阶梯形变截面桩响应的简化解析算法,可以得到桩身内力及变形的分布情况,且可以反映桩身几何参数对桩身内力、变形分布的影响,为优化阶梯形变截面桩的桩身几何结构提供了参考.
(3)当桩身结构趋近刚性变形(减小长径比)时,桩身最大水平位移逐渐减小,而最大弯矩增大,同时弯矩峰值点与反弯点所在位置均向桩底移动.
(4)变径位置由桩顶向桩底逐步下移的过程中,弯矩峰值点与反弯点位置均向桩底移动,同时桩身弯矩峰值逐渐增大,桩顶最大水平位移减小;在变径位置下降至40%后,继续下移变径位置对桩身最大水平位移的影响很小,可见当上部扩大直径段长度所占比例超过40%时对提高桩身水平承载能力无显著效果.
(5)当桩顶位移未超过桩身容许位移时,减小下部桩径有利于减小桩身弯矩峰值,更有效地协调桩身变形,避免应力集中.
参考文献
Behavior of step tapered bored piles in sand under static lateral loading
[J].DOI:10.1061/(ASCE)GT.1943-5606.0000265 [本文引用: 9]
双层地基水平受荷桩受力变形分析
[J].
Analysis of the deformation of the horizontally loaded piles on the double-layered foundation
[J].
Behavior of laterally loaded piles in multilayered soils
[J].DOI:10.1061/(ASCE)GM.1943-5622.0000319 [本文引用: 2]
Analysis of laterally loaded piles in clay using DMT
[J].
Hyperbolic P-Y criterion for cohesive soils
[J].
砂土中水平受荷桩非线性分析
[J].
Sandy soil nonlinear analysis of horizontally loaded piles
[J].
Methods for deriving p-y curves from instrumented lateral load tests
[J].
A simplified nonlinear method for a laterally loaded pile in sloping ground
[J].
斜坡基桩p-y曲线及水平承载计算方法研究
[J].
Study on calculation method of p-y curve and horizontal load of slope foundation piles
[J].
Laterally loaded piles: program documentation
[J].
Generalized solutions for laterally loaded piles
[J].
Mechanical response of bridge piles in high-steep slopes and sensitivity study
[J].DOI:10.1007/s11771-015-2948-1 [本文引用: 1]
基于有限杆单元法的陡坡段桥梁基桩受力分析
[J].DOI:10.3969/j.issn.1001-7372.2014.06.007
Mechanical analysis of piles on steep slopes based on finite element method
[J].DOI:10.3969/j.issn.1001-7372.2014.06.007
考虑陡坡效应的横向受荷桩受力分析纽玛克解答
[J].DOI:10.3969/j.issn.1002-0268.2014.10.010 [本文引用: 1]
Stress analysis of laterally loaded piles taking into account the effect of steep slopes Newmark's solution
[J].DOI:10.3969/j.issn.1002-0268.2014.10.010 [本文引用: 1]
Soil modulus for laterally loaded piles
[J].
The response of flexible piles to lateral loading
[J].DOI:10.1680/geot.1981.31.2.247 [本文引用: 1]