滤波器组多载波技术^[1-5]作为5G基础波形的重要候选者之一，它以更好的抗衰落性和良好的频谱选择特性得到广泛关注. 相比于正交频分复用（orthogonal frequency division multiplexing，OFDM）技术最大的不同在于它采用更优的原型滤波器代替矩形窗函数，降低带外衰减. 滤波器组多载波（filter bank multicarrier，FBMC）系统不需要额外的循环前缀，可以节约约1/4的频谱资源. FBMC系统虚部干扰问题的存在直接影响了信道估计的准确性，制约了系统的性能.

FBMC系统的信道估计方案有干扰近似法（interference approximation method，IAM）和干扰消除法（interference cancellation method，ICM）. 其中，ICM方案应用广泛，它是根据原型滤波器组的干扰系数设计能够相互抵消虚部干扰的导频分布. Lele等^[6]提出使用辅助导频方案（aided pilot，AP），在导频周围添加额外的辅助导频符号来消除周围其他数据符号对该导频产生的虚部干扰. 陈孝武^[7]通过增加辅助导频符号数量，对原有AP方案进行改进.

将深度学习应用到移动通信系统中的概念刚刚起步，前期研究内容主要是将深度学习理论引入无线资源管理和分配等领域. Ye等^[8]尝试在OFDM系统中采用深度模型进行信道估计和信号检测，但由于虚部干扰问题的存在，该方法无法直接应用到FBMC系统中. Ye等^[9]研究基于深度学习算法的信道解码，证实在没有先验信道信息（channel state information，CSI）的情况下，利用深度模型可以学习出复杂的编码方式用于解码，提升了系统性能. Cheng等^[10]首次将应用在图像中的残差网络模型运用到FBMC-偏移正交幅度调制（OQAM）系统中进行信道估计和均衡. 利用Res-DNN模型强大的学习能力，BER性能远远优于其他如IAM、CP-OFDM以及基于传统深度神经网络（deep neural networks，DNN）模型的方案. Cao等^[11]介绍了文本分类任务中的TextCNN模型，该模型对句子中单词之间的关联特征有良好的提取能力.

本文提出基于深度学习的信道估计与检测的方法，搭建完整的FBMC-OQAM与深度学习模型结合的仿真系统. 本文的创新点如下.

1）提出利用one-hot编码思想设计接收信号的特征矩阵和训练样本的标签矩阵.

2）使用ResNet-DNN神经网络模型对信道符号检测模块建模. 本文提出的ResNet-DNN模型在文献[10]的基础上作出以下改动：由原来2层简单的残差层重新设计为更加复杂的3层残差网络；根据文献[12]，对模型参数进行优化与调整；该模型仅仅应用于符号检测模块，不进行对信道的估计.

3）在文献[11]模型的基础上改进通道数量、卷积核大小等结构和参数，提出CNN+NN的融合模型. 在通信系统的接收端（信道估计、均衡、符号检测），提出采用CNN+NN模型进行建模和集成，提高了信道估计的BER性能.

FBMC-OQAM系统在发射端将QAM符号的实部和虚部拆开进行交替发送，窄带信号合成为宽带信号. FBMC-OQAM系统的框架示意图如图1所示. 图中，n为时间索引，M为子载波数量。假设输入信号为复数序列，数学表达式如下：

(1) $x[k] \!=\! \sum\limits_{m = 0}^{M - 1} {\sum\limits_{n \in Z} }{{a_{m,n}}g} \left[{k\!\! -\!\! n{M}/{2}} \right]{\exp\,\left( {\frac{{{\rm j}2{\text{π}} mk}}{M}}\right)}{\exp\,\left( {\frac{{{\rm j}2{\text{π}} (m + n)}}{2}}\right)}.$

式中： ${a_{m,n}}$为在时间频率索引上 $(m,n)$的发送符号； $m$为频率索引； $n$为时间索引； $g[k]$为载波的原型滤波器，

(2) ${g_{m,n}}[k] = g\left[k - n{M}/{2}\right]{\exp\,\left({\frac{{{\rm j}2{\text{π}} mk}}{M}}\right)}{\exp\,\left({\frac{{{\rm j}2{\text{π}} (m + n)}}{2}}\right)}.$

假设FBMC-OQAM系统传输的信道是慢时变的，即在一个符号间隔，信道是不变的. ${H_{m,n}}$为第 $m$个子载波在第 $n$个时间块上符号所经过的信道增益，高斯白噪声（white Gaussian noise，WGN）的方差为 ${\sigma ^{\rm{2}}}$. 在接收端第 $m$个子载波在第 $n$个时间块上的接收符号为

(3) ${\overline a _{_{m,n}}} = {H_{m,n}}({a_{m,n}} + {\rm j}{a^{(*)}}_{m,n}) + {\eta _{m,n}}.$

式中： ${\eta _{m,n}}$为信道噪声， ${a^{(*)}}$为由周围数据符号 ${a_{m,n}}$所产生的虚部干扰. AP方案在导频附近添置辅助导频来消除 ${a^{(*)}}$.

传统的符号检测模块是采用星座图进行判别的，即接收端收到的信号经过解调、信道估计等操作转换成符号信号；利用简单的判别算法，根据符号到星座点的欧氏距离，将每一个符号判别成离它最近的星座点. 欧式距离的计算方法为

(4) $ d(x,y) = \sqrt {\sum\limits_{k = 1}^{\rm{2}} {{{({x_k} - {y_k})}^2}} } . $

式中： ${x_k}$为接收符号信号， ${y_k}$为星座点坐标. 该方法中将每一个样本 $x$判别成最近距离的星座点 $y$.

近年来，随着深度学习的崛起，其在很多应用领域都带来了性能的显著提升. 神经网络可以是任意函数的逼近器，有很强的函数学习能力，且神经网络的训练可以离线操作然后保存模型，使用时只需要调用模型，保证通信低时延的要求，因此能够实现将深度学习应用于信道符号检测模块和部分接收端模块中.

接收数据在星座空间上有明显的空格位置特征，这些特征与信道信息和噪声有关，且特征在通过信道传输到接收端时可以有一定程度的保留. 相较于传统的符号检测模块，深度学习具有良好的特征提取能力. 此外，深度模型学习到的判别规则可以预测出训练集未曾出现的值，这相当于模型有一定的纠错能力. 受到深度学习模型的输入限制，需要对接收端的数据进行预处理.

特征处理：符号映射的直接关系是接收到的数据，噪声作为干扰项对它有一定影响. 在真实环境中噪声功率信息未知，因此采用接收到的真实数值进行特征的设计. 由于接收数据是复数值，相当于连续的数值，文本采用one-hot编码的思想对接收信号进行离散化. 具体操作如表1所示.

标签处理：每个接收到的符号对应一个原始数据标签. 由于OQAM调制阶数N=16，一共有16种可能标签. 16种标签分别对应0000，0001，0010，0011，···，1111. 每一个不同的标签对应一组1×4的矩阵，只含有0和1，对应原始的数据比特流.

单个特征矩阵一共18行（（2+6+1）×2），每一行代表一个数值，每个数值采用one-hot编码，数值的可能性为0、1、2、3、4、5、6、7、8、9、+、−总共12种可能性，所以每个数值编码后是12维度. 最终的数据集形式为每一个数据样本的特征是18×12的特征矩阵，1×4的标签矩阵. 根据该类数据集进行模型的训练，使用模型去判别新的接收符号数据所对应的标签.

深度神经网络可以称为多层感知机（multi layer perceptron，MLP），主要由输入层、隐藏层和输出层组成. 隐藏层可以包含多个层，层与层之间都是全连接的，即第i层的任意一个神经元与第i+1层的任意一个神经元相连接. 层数越多，随之而来的是更高的计算复杂度、梯度消失（vanishing）和梯度爆炸（exploding）问题. 为了解决这些问题，Cheng等^[10]提出残差学习结构（ResNet）. 在ResNet的实现中，每两层添加一个快捷连接（shortcut connection，SC）. 神经网络只需要输入 $x$以及映射后的差值：

(5) $F(x) = H(x) - x.$

神经网络直接拟合残差函数，比直接拟合 $H(x)$容易. 在ILSVRC2015竞赛中，残差网络针对图像识别和检测中获得第一，证明了残差的网络结构拥有良好的性能. 提出ResNet-DNN网络模型用于符号检测.

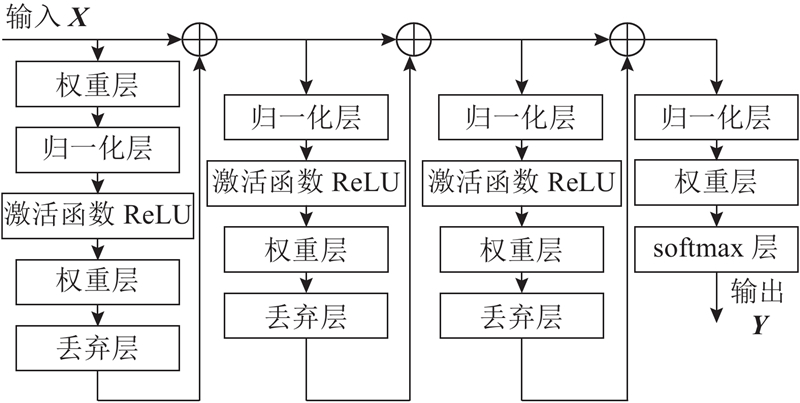
如图2所示，本文仿真的深度学习模型采用3层残差层，第1个残差结构是全连接层、归一化层（BN）、ReLU、全连接层以及Dropout层. 后面2个残差结构是归一化、ReLU、全连接层、Dropout层. 经过这3个残差网络后的输出再经过一个归一化层、全连接层和softmax层，最终输出为16维度的概率序列.

采用ReLU作为激活函数，它被证实在多种经典网络，如卷积神经网络（convolutional neural networks，CNN）、长短期记忆网络（long short-term memory，LSTM）等模型中效果优异，能够解决正区间梯度消失问题，加快训练速度. ReLU函数的数学表达式如下所示：

(6) $f(x) = \max\; \{ 0,x\} .$

采用交叉熵作为损失函数，可以在梯度下降时避免学习速率降低的问题，如下所示：

(7) $H(p) = \sum\limits_i {p(i) \log\; \left({{q(i)}^{-1}}\right)} .$

式中： $p(i)$为正确标签， $q(i)$为预测标签， $H(p)$为刻画两者分布之间的距离.

由于深度学习模型的损失函数是凸函数，不能直接求解最小值对应的参数，需要优化器对参数进行迭代. Adam优化器是一种自适应参数更新算法，对超参数的选择具有高鲁棒性，数学表示如下：

(8) $\begin{split} \left. \begin{array}{l} {m_t} = {\beta _1}{m_{t - 1}} + (1 - {\beta _1}){g_t},\;{v_t} = {\beta _2}{v_{t - 1}} + (1 - {\beta _1})g_t^2, \\ {{\hat m}_t} = {{{m_t}}}/({{1 - \beta _1^t}}),\;{{\hat v}_t} = {{{v_t}}}/({{1 - \beta _2^t}} ), \\ {\theta _{t + 1}} = {\theta _t} - {\eta }{{\hat m}_t}/({{\sqrt {{{\hat v}_t}} + \varepsilon }}). \end{array} \right\}\end{split} $

式中： ${m_t}$和 ${v_t}$分别为一阶动量和二阶动量项；β₁和β₂分别为动力值，通常取0.9和0.999； ${\hat m_t}$和 ${\hat v_t}$分别为各自的修正值； ${\theta _t}$为 $t$时刻第 $t$迭代模型的参数；ε通常取很小的值.

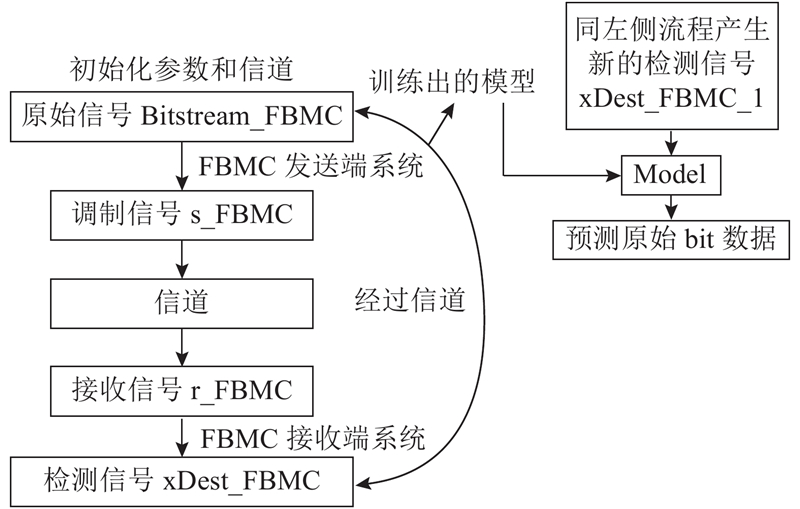
提出将FBMC-OQAM系统与ResNet-DNN网络模型结合，搭建完整的仿真系统，如图3所示.

具体的符号检测流程共分为8个步骤，其中的变量名分别对应仿真代码里的变量名，如表2所示.

将模型用于同左侧流程一样操作的新的检测信号xDest_FBMC_1中，预测新的原始比特数据流. 虽然在训练过程中，花费了大量的时间成本，但是在预测新的比特数据时只需直接调用模型，不必花额外的计算时间，因此不会降低原来检测符号的速度.

采用的仿真环境是Python，版本为Python3.6，仿真过程中所用到库及其版本为Matplotlib2.1.2、Numpy1.14.0、Keras2.1.5、Tensorflow1.7.0. 通信仿真参数如表3所示.

ResNet-DNN网络模型的仿真参数如表4所示.

根据表3、4所示的初始化参数进行仿真. 本文仿真产生的训练数据集为135 000个，由于模型的输出数据维度要求，将每个样本18×12的二维特征转变成216特征，最终的输入数据的特征是135 000×216矩阵，标签是135 000×4矩阵.

深度学习中同一模型在不同训练集上学得的函数往往是不同的，为了保证选出的模型是最优的，采用交叉验证法. 将样本集随机分成5份，每份数据中27 000个，每次采用其中4份作为训练集，另外一份作为验证集，重复5次，将验证集上5次的误差平均值作为模型的误差. 在训练集上的准确率为93.2%，在验证集上的准确率为88.7%.

ResNet-DNN模型的计算复杂度（只计算全连接层和ReLU层），单位为 FLOPS（floating point operations per second，每秒浮点运算数）. 仿真设备如下：Intel（R）Core（TM）i7-6700HQ CPU @2.60 GHz，内存（RAM）为8 GB，64位操作系统. 原始分类器的时间复杂度可以忽略不计，计算复杂度为6 FLOPS；神经网络模型训练时的时间复杂度约为700 s，计算复杂度约为611 796 FLOPS，单个新样本的预测时间约为0.156 ms.

利用ResNet-DNN模型大大增加了计算和时间复杂度，但是对新样本的预测所用时间极少，能够满足通信低延迟的要求.

如图4所示，在加性高斯白噪声信道下，对原FBMC-OQAM系统结合神经网络模型进行仿真实验. 图中，SNR为信噪比. 采用8个离散型导频，估计信道时使用线性插值补充未知信道. 从图4可以看出，在基于导频的信道估计方法中，采用ResNet-DNN模型替代原先的分类器大幅提升了BER性能；在信道已知的情况下（方形实线和上三角虚线），ResNet-DNN模型的BER性能可以逼近理论值，甚至在个别信噪比值上神经网络模型的BER会略微优于理论值. 实验分析得模型可以预测训练集未曾出现的值和模型强大的鲁棒性，相当于在判别原始数据时有一定的校正能力.

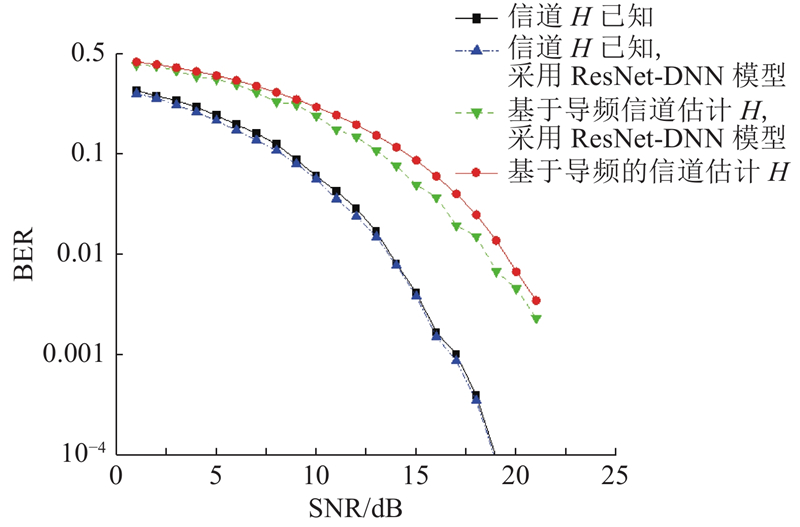
图5中采用的行人速度下的信道模型（PedestrianA信道）在时间上是平坦的，在频域上是变化的，因此在该信道下的信道估计更具有挑战性. 在本文的仿真实验中，PedestrianA信道为30径，放置30个离散型导频. 采用ResNet-DNN模型后，BER得到一定的改善，可见深度学习模型适合于频域上慢变化的信道.

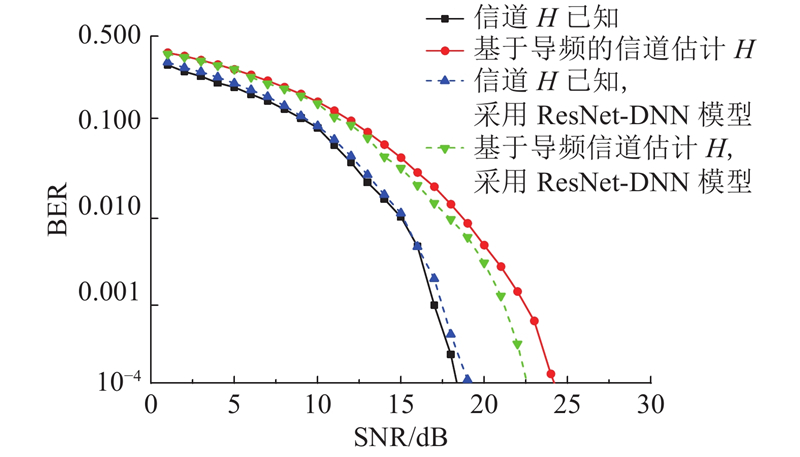
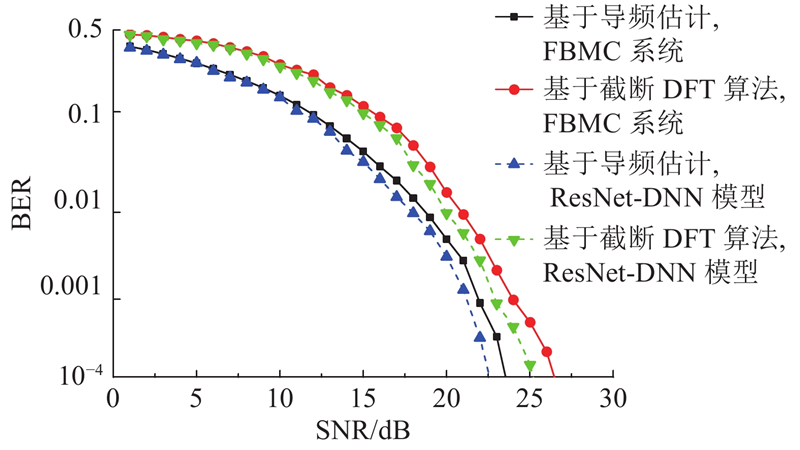
如图6所示为FBMC系统增加经典DFT算法的BER性能比较，可得DFT算法较普通FBMC的信道估计BER性能略差，这是因为DFT算法在PAPR性能上有一定的改善. 使用DFT算法将原始分类器替换成ResNet-DNN模型后，BER性能有一定的提升.

FBMC系统中存在的虚部干扰问题，对信道估计产生严重的负面影响. 在FBMC-OQAM中，每个QAM符号的实部和虚部被分离，并作为一对脉冲幅度调制（PAM）进行传输. 在接收端所接收到的是复数信号，复数的虚部来自于周围数据符号的符号间干扰（ISI）和载波间干扰（ICI）. 将ISI和ICI部分统一称为虚部干扰（imaginary interference）. 虚部干扰会引发在进行信道估计时产生严重的负面影响. 在没有对虚部干扰进行事先抵消或抑制的情况下，FBMC-OQAM中的信道估计是一个很大的挑战. 从式（3）可知，在接收端的第 $m$个子载波和第 $n$个时间块上符号表示为

(9) $ a_{m,n}^{(*)} = \sum\limits_{(p,q) \ne (0,0)} {{a_{m + p,n + q}}} \psi \{ \zeta _{m + p,n + q}^{m,n}\} . $

式中： $ \psi {{\{ }}\zeta _{{{m}} + {{p}},{{n}} + {{q}}}^{m,n}{{\} }}$为 ${a_{{{m}} + {{p,n}} + {{q}}}}$对于 ${a_{m,n}}$产生的虚部干扰系数. 目前，虚部消除方案主要有辅助导频^[13-14]、编码（coding）、编码辅助导频^[15]等. 本文提出采用CNN+NN模型代替部分接收端模块（信道估计、均衡模块及符号检测），大大提升了BER性能. 相较于符号检测的流程，部分接收端模块在训练模型时采用的数据集标签不变，特征直接采用在接收端经过解调后的信号.

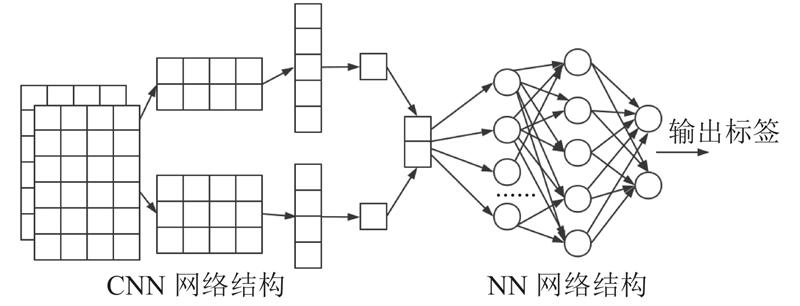
采用的CNN+NN模型借鉴于TextCNN模型. TextCNN模型在文本分类任务中取得不错的效果，证实了网络结构良好的性能，结构如图7所示.

如图7所示，左边是CNN网络模型结构，右边是简单的NN网络模型结构. CNN结构类似图像处理，第一层是embedding层，即二维n×m的图像矩阵，每行是数值对应的embedding向量；经过卷积层，由2个通道组成，每一个通道的卷积核尺寸都不一样，分别对原始的二维矩阵进行卷积操作；接着经过池化层，采用max-pooling池化；然后将输出结果经过全连接层网络；最后通过softmax层输出概率向量结果.

采用的通信仿真参数如表3所示，CNN+NN模型的参数如表5所示.

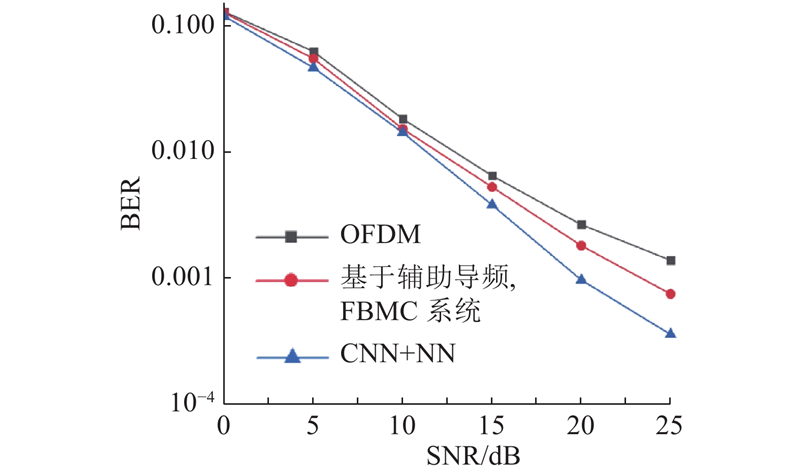
如图8所示为在AWGN信道下的仿真结果. 方块实线是CP-OFDM的仿真结果，BER性能最差；圆形实线是FBMC系统采用辅助导频方案的结果；三角形实线是在FBMC系统中基于CNN+NN模型的信道估计，BER性能有大幅度的提升.

本文对接收数据符号进行特征预处理，结合FBMC-OQAM系统和神经网络模型，搭建完整的仿真系统，改进的网络模型适用于加性高斯白噪声信道和时不变信道中，但不适用于时变信道. 结果表明，相较于传统方案，RseNet-DNN模型大大提升了BER及系统性能. 这是一种崭新的思路，不必人为设计复杂的通信系统以及单独设计每个模块结构，基于深度学习模型本身较强的学习能力，从数据中挖掘内在的规则，以此来优化通信系统，实现可靠、高效的安全传输，是未来通信领域研究的热门方向.