[1]
MAIDL B, SCHMID L, RITZ W, et al. Hardrock tunnel boring machines [M]. [S. l.]: Wiley, 2008.
[本文引用: 1]
[2]
王超. TBM岩机映射关系及其优化决策方法研究[D]. 杭州: 浙江大学, 2018.
WANG Chao. Research on the relationship of rock type and machine parameters of TBM and its optimal decision method [D]. Hangzhou: Zhejiang University, 2018.
[3]
YIMIN X, DUAN Y, CHENGHUAN H, et al Numerical simulation of ventilation and dust suppression system for open-type TBM tunneling work area
[J]. Tunnelling and Underground Space Technology , 2016 , 56 (3 ): 70 - 78
[4]
周赛群. 全断面硬岩掘进机(TBM)驱动系统研究[D]. 杭州: 浙江大学, 2008.
ZHOU Sai-qun. Study on drive system of the full-face tunnel boring machine [D]. Hangzhou: Zhejiang University, 2008.
[5]
刘然. 盾构机刀盘同步驱动系统自适应均载控制研究[D]. 大连: 大连理工大学, 2013.
[本文引用: 1]
LIU Ran. Research on adaptive load sharing control for sychronous driving system of cutterhead in shield machines [D]. Dalian: Dalian University of Technology, 2013.
[本文引用: 1]
[6]
BARLA G, PELIZZA S. TBM tunnelling in difficult ground conditions [C]// ISRM International Symposium . Melbourne: International Society for Rock Mechanics and Rock Engineering, 2000.
[本文引用: 1]
[7]
OKUBO S, FUKUI K, CHEN W Expert system for applicability of tunnel boring machines in Japan
[J]. Rock Mechanics and Rock Engineering , 2003 , 36 (4 ): 305 - 322
DOI:10.1007/s00603-002-0049-6
[本文引用: 1]
[8]
HASSANPOUR J, ROSTAMI J, KHAMEHCHIYAN M, et al Developing new equations for TBM performance prediction in carbonate-argillaceous rocks: a case history of Nowsood water conveyance tunnel
[J]. Geomechanics and Geoengineering , 2009 , 4 (4 ): 287 - 297
DOI:10.1080/17486020903174303
[本文引用: 1]
[9]
HASSANPOUR J, ROSTAMI J, KHAMEHCHIYAN M, et al TBM performance analysis in pyroclastic rocks: a case history of Karaj water conveyance tunnel
[J]. Rock Mechanics and Rock Engineering , 2010 , 43 (4 ): 427 - 445
DOI:10.1007/s00603-009-0060-2
[本文引用: 1]
[10]
熊帆. 基于 PSO-SVR 算法的 TBM 掘进效率预测及围岩分级研究[D]. 西安: 长安大学, 2016.
[本文引用: 1]
XIONG Fan. Research of TBM excavation efficiency prediction and rock classification based on the PSO-SVR algorithm [D]. Xi’an: Chang’an University, 2016.
[本文引用: 1]
[11]
罗华. 基于线性回归和深度置信网络的 TBM 性能预测研究[D]. 杭州: 浙江大学, 2018.
[本文引用: 1]
LUO Hua. Application of linear regression analysis and deep belief network for performance prediction of TBM [D]. Hangzhou: Zhejiang University, 2018.
[本文引用: 1]
[12]
杜立杰, 齐志冲, 韩小亮, 等 基于现场数据的TBM可掘性和掘进性能预测方法
[J]. 煤炭学报 , 2015 , 40 (6 ): 1284 - 1289
[本文引用: 1]
DU Li-jie, QI Zhi-chong, HAN Xiao-liang, et al Prediction method for the boreability and performance of hard rock TBM based on boring data on site
[J]. Journal of China Coal Society , 2015 , 40 (6 ): 1284 - 1289
[本文引用: 1]
[15]
张娜, 李建斌, 荆留杰, 等 TBM掘进参数智能控制系统的研究与应用
[J]. 隧道建设 , 2018 , 38 (10 ): 1734 - 1740
DOI:10.3973/j.issn.2096-4498.2018.10.019
[本文引用: 1]
ZHANG Na, LI Jian-bin, JING Liu-jie, et al Study and application of intelligent control system of TBM tunneling parameters
[J]. Tunnel Construction , 2018 , 38 (10 ): 1734 - 1740
DOI:10.3973/j.issn.2096-4498.2018.10.019
[本文引用: 1]
[16]
YAGIZ S, GOKCEOGLU C, SEZER E, et al Application of two non-linear prediction tools to the estimation of tunnel boring machine performance
[J]. Engineering Applications of Artificial Intelligence , 2009 , 22 (4/5 ): 808 - 814
[本文引用: 1]
[17]
JAMSHIDI A Prediction of TBM penetration rate from brittleness indexes using multiple regression analysis
[J]. Modeling Earth Systems and Environment , 2018 , 4 (1 ): 383 - 394
DOI:10.1007/s40808-018-0432-2
[本文引用: 1]
[18]
GHASEMI E, YAGIZ S, ATAEI M Predicting penetration rate of hard rock tunnel boring machine using fuzzy logic
[J]. Bulletin of Engineering Geology and the Environment , 2014 , 73 (1 ): 23 - 35
DOI:10.1007/s10064-013-0497-0
[本文引用: 1]
[19]
JAVAD G, NARGES T Application of artificial neural networks to the prediction of tunnel boring machine penetration rate
[J]. Mining Science and Technology (China) , 2010 , 20 (5 ): 727 - 733
DOI:10.1016/S1674-5264(09)60271-4
[本文引用: 1]
[20]
王超, 龚国芳, 杨华勇, 等 NSVR 硬岩隧道掘进机刀盘扭矩预测分析
[J]. 浙江大学学报:工学版 , 2018 , 52 (3 ): 479 - 486
[本文引用: 1]
WANG Chao, GONG Guo-fang, YANG Hua-yong, et al NVSR based predictive analysis of cutterhead torque for hard rock TBM
[J]. Journal of Zhejiang University: Engineering Science , 2018 , 52 (3 ): 479 - 486
[本文引用: 1]
[21]
吴煜宇, 吴湘滨, 尹俊涛 关于 TBM 施工隧洞围岩分类方法的研究
[J]. 水文地质工程地质 , 2006 , 33 (5 ): 120 - 122
DOI:10.3969/j.issn.1000-3665.2006.05.028
[本文引用: 1]
WU Yu-yu, WU Xiang-bin, YIN Jun-tao Research with relation to rock classification of TBM Tunnels
[J]. Hydrogeology and Engineering Geology , 2006 , 33 (5 ): 120 - 122
DOI:10.3969/j.issn.1000-3665.2006.05.028
[本文引用: 1]
1
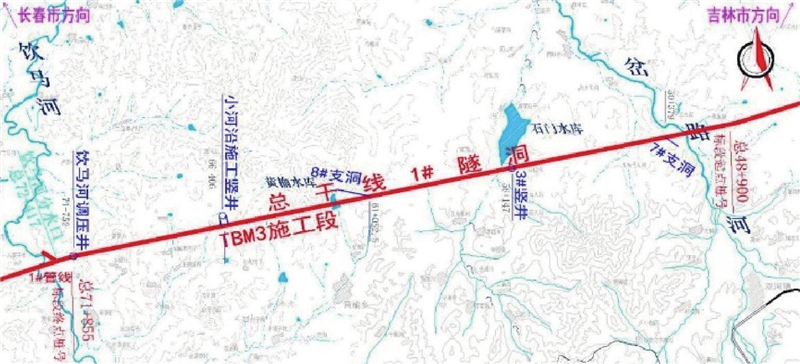
... 硬岩隧道掘进机(tunnel boring machine,TBM)又称为全断面硬岩隧道掘进机,是一种自动化水平较高的大型特种隧道掘进装备[1 -5 ] . 目前,我国使用TBM工法进行隧道施工,还需要工人对隧道掘进机进行控制,但依赖人工经验进行操作参数决策将导致隧道施工的质量出现不同. 优秀的TBM司机可以达到更好的施工效果,经验欠缺的司机不行. 在一些极端条件下,由于司机经验的欠缺,会导致TBM掘进不平稳、卡机、坍塌等严重后果,造成工期延误和重大的经济损失[6 ] . ...
Numerical simulation of ventilation and dust suppression system for open-type TBM tunneling work area
0
2016
1
... 硬岩隧道掘进机(tunnel boring machine,TBM)又称为全断面硬岩隧道掘进机,是一种自动化水平较高的大型特种隧道掘进装备[1 -5 ] . 目前,我国使用TBM工法进行隧道施工,还需要工人对隧道掘进机进行控制,但依赖人工经验进行操作参数决策将导致隧道施工的质量出现不同. 优秀的TBM司机可以达到更好的施工效果,经验欠缺的司机不行. 在一些极端条件下,由于司机经验的欠缺,会导致TBM掘进不平稳、卡机、坍塌等严重后果,造成工期延误和重大的经济损失[6 ] . ...
1
... 硬岩隧道掘进机(tunnel boring machine,TBM)又称为全断面硬岩隧道掘进机,是一种自动化水平较高的大型特种隧道掘进装备[1 -5 ] . 目前,我国使用TBM工法进行隧道施工,还需要工人对隧道掘进机进行控制,但依赖人工经验进行操作参数决策将导致隧道施工的质量出现不同. 优秀的TBM司机可以达到更好的施工效果,经验欠缺的司机不行. 在一些极端条件下,由于司机经验的欠缺,会导致TBM掘进不平稳、卡机、坍塌等严重后果,造成工期延误和重大的经济损失[6 ] . ...
1
... 硬岩隧道掘进机(tunnel boring machine,TBM)又称为全断面硬岩隧道掘进机,是一种自动化水平较高的大型特种隧道掘进装备[1 -5 ] . 目前,我国使用TBM工法进行隧道施工,还需要工人对隧道掘进机进行控制,但依赖人工经验进行操作参数决策将导致隧道施工的质量出现不同. 优秀的TBM司机可以达到更好的施工效果,经验欠缺的司机不行. 在一些极端条件下,由于司机经验的欠缺,会导致TBM掘进不平稳、卡机、坍塌等严重后果,造成工期延误和重大的经济损失[6 ] . ...
Expert system for applicability of tunnel boring machines in Japan
1
2003
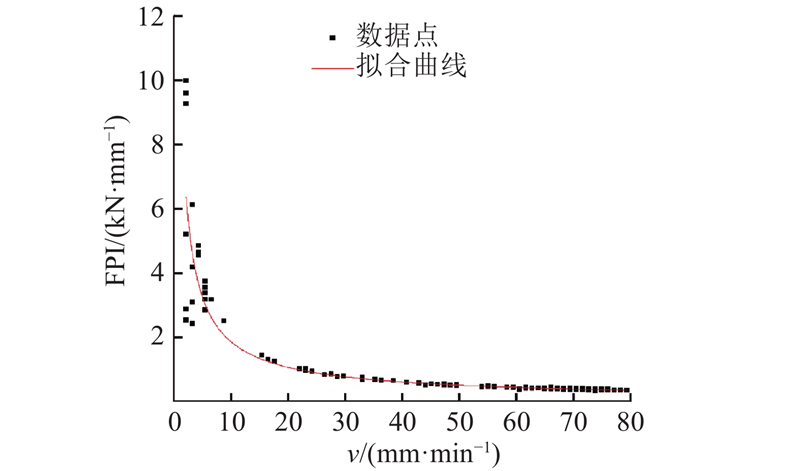
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
Developing new equations for TBM performance prediction in carbonate-argillaceous rocks: a case history of Nowsood water conveyance tunnel
1
2009
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
TBM performance analysis in pyroclastic rocks: a case history of Karaj water conveyance tunnel
1
2010
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
1
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
1
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
1
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
1
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
基于现场数据的TBM可掘性和掘进性能预测方法
1
2015
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
基于现场数据的TBM可掘性和掘进性能预测方法
1
2015
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
盾构机掘进过程中的决策支持系统
1
2011
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
盾构机掘进过程中的决策支持系统
1
2011
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
Residual analysis in inverse identification of total thrust on shield tunneling machine
1
2013
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
TBM掘进参数智能控制系统的研究与应用
1
2018
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
TBM掘进参数智能控制系统的研究与应用
1
2018
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
Application of two non-linear prediction tools to the estimation of tunnel boring machine performance
1
2009
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
Prediction of TBM penetration rate from brittleness indexes using multiple regression analysis
1
2018
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
Predicting penetration rate of hard rock tunnel boring machine using fuzzy logic
1
2014
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
Application of artificial neural networks to the prediction of tunnel boring machine penetration rate
1
2010
... 得益于近年来TBM工法的广泛使用,施工企业可以轻易获取海量的掘进数据. 在围岩级别已知、TBM掘进状态正常的条件下,依据TBM大量的历史掘进数据进行地质预测和操作参数进行决策,成为相关企业、高校研究的热点. Okubo等[7 ] 使用修正的岩机关系模型,建立TBM操作参数的专家选择系统. Hassanpour等[8 -9 ] 基于不同隧道的实际施工数据,研究围岩单轴抗压强度、围岩节理参数与掘进参数的关系,定义场切深指数(field penetration index, FPI);熊帆[10 ] 依据FPI理论建立PSO-SVR模型,用于预测FPI,根据FPI和统计学的方法选择隧道掘进机的操作参数;罗华[11 ] 使用深度置信网络模型对FPI搭建预测模型. 杜立杰等[12 ] 通过研究围岩的参数与FPI的关系,建立围岩属性推导施工参数选择的经验公式. 李守巨等[13 ] 针对不同的地层数据,提出相应的掘进机操作参数选择方案,优化了掘进效率,降低了刀具的磨损. Chen等[14 -15 ] 使用残差分析并结合回归分析以及神经网络等方法,依托工程数据建立掘进机负载预测模型. Yagiz 等[16 ] 在工程数据的基础上,建立岩石脆性指数预测模型. Jamshidi[17 ] 使用多元回归分析的方法,建立TBM切深与围岩脆性指数的回归预测模型. Ghasemi 等[18 ] 通过对单轴抗压强度、抗拉强度和弱点之间的距离等建立模糊模型,对TBM的性能进行观测;Javad等[19 ] 使用人工智能神经网络的方法,对硬岩掘进机的FPI进行预测,以获得围岩级别的信息. 上述研究都以FPI作为围岩级别特征参数,证明了围岩级别特征参数通过人工智能的方法能够得到有效预测. 由于FPI与围岩级别的非线性关系,在识别围岩级别时会出现错误. ...
NSVR 硬岩隧道掘进机刀盘扭矩预测分析
1
2018
... 辨别TBM是否停机维护,只需要判断总推进力 $F$ $v$ $T$ $n$ [20 ] 为 ...
NSVR 硬岩隧道掘进机刀盘扭矩预测分析
1
2018
... 辨别TBM是否停机维护,只需要判断总推进力 $F$ $v$ $T$ $n$ [20 ] 为 ...
关于 TBM 施工隧洞围岩分类方法的研究
1
2006
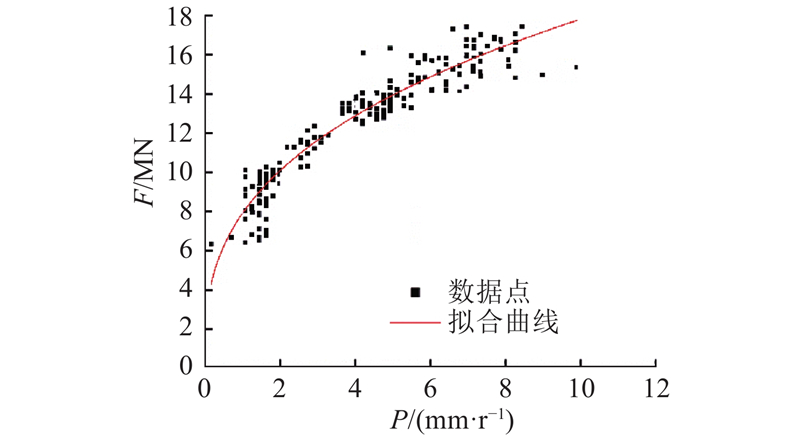
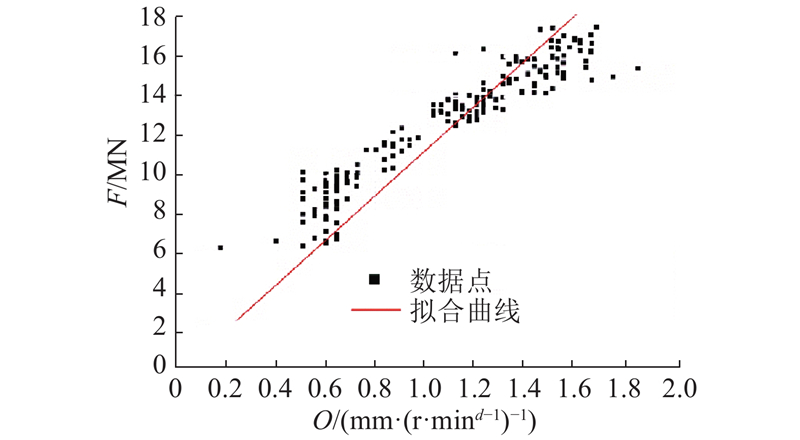
... 在掘进过程中,操作参数、围岩级别、掘进状态构成了施工数据的闭环. 在理论情况下,当操作参数一定时,掘进总推进力 $F$ $T$ [21 ] ,定义为 ...
关于 TBM 施工隧洞围岩分类方法的研究
1
2006
... 在掘进过程中,操作参数、围岩级别、掘进状态构成了施工数据的闭环. 在理论情况下,当操作参数一定时,掘进总推进力 $F$ $T$ [21 ] ,定义为 ...