随着智能交通信息、网络社交技术的迅猛发展，城市智慧交通理念应运而生. 与原有固化交通管控方法不同，智慧交通采用多种科学有效的动态交通管控手段（如：动态交通信号控制^[1]、动态交通拥挤收费^[2]等）. 随着智慧交通数据的实时获取和交通管控措施的动态调整，交通出行行为决策（包括出行目的地、出行方式、出行路径和出发时刻）过程随之实时变化，导致道路交通流量也呈现动态演化状态.

交通流量分布是所有出行者的出行过程在道路网络上的集计，从本质上来看，交通流量分布状态是由出行者个体所决定的. 在过去几十年内，许多方法被用来研究出行者行为. 假设每个出行者都选择路径时间最小的出行路线，20世纪50年代Wardrop^[3]据此提出了用户均衡（user equilibrium，UE）理论. 考虑到出行者对路径出行时间的感知具有一定的随机误差，Daganzo等^[4]提出了随机用户均衡（stochastic user equilibrium，SUE）模型. 许多学者利用随机环境下的交通网络均衡模型来描述交通系统中的不确定因素^[5-6]；近年来，交通学者认为出行者不仅关注当前网络状况，往往还考虑自己以往的出行经验，因此提出了逐日动态交通均衡模型^[7-8].

近年来，交通出行演化模型一直受到国内外交通学者的广泛关注. 根据稳定状态的不同，模型可以分为UE型和SUE型演化模型. UE型出行行为决策机制的研究主要包括Smith比例调整过程^[9]、改进Smith比例调整过程^[10]、网络纠错过程^[11]、投影动态调整过程^[12]、先进先出规则^[13]、Brown-von Neumann-Nash调整过程^[14]和理性行为调整过程^[15]. Watling等^[16-18]在SUE型出行行为决策机制上作了很多研究. 关于其他类型的出行演化模型，Guo等^[19-20]提出了有限理性下交通流逐日演化模型. Ye等^[21]进一步将该模型扩展到理性行为调整过程中. Cheng等^[8]研究了先进出行者信息系统下的动态交通演化过程. 刘天亮等^[22-23]在交通量逐日演化模型的基础上考虑出行者风险行为，建立了基于出行风险的交通演化模型.

多样的交通检测技术为交通系统提供了丰富的路网数据. 运用一定的准则融合多源交通数据，并进行交通决策，已成为当前交通领域发展的重要方向. 通常情况下，多源数据融合技术可以降低数据多样化带来的模棱两可，并弥补单一数据存在的不足与缺失问题，因此多源数据比单一数据的决策效果更加全面、准确^[24]. 数据融合算法主要有Dempster-Shafer证据理论法^[25]、卡尔曼滤波法^[26]、加权平均法^[27]、人工智能法^[28]等. 由于多源信息和数据融合技术的特殊性与复杂性，面对不同结构的观测数据，各种融合算法具有各自的使用局限性.

上述文献运用不同方法对动态交通演化模型进行了研究，存在一些不足：1）智慧公路实时提供道路网络运行状况，已有交通演化研究没有考虑智慧公路对模型的影响；2）多源数据融合技术在各个领域得到了快速发展，但很少有研究将数据融合技术应用到路径选择行为建模上；3）已有智慧公路的研究均从实际工程应用角度出发，缺乏从理论角度深入解析智慧公路与交通网络设计的关系.

为此，本文研究路网中同时存在普通公路和智慧公路的情况下居民出行的交通演化过程，其中普通公路上的出行者在选择路径时，不仅考虑预测的路网出行时间，还考虑自身的出行经验；智慧公路提供多源数据，通过融合交通数据，出行者获得实时路网出行时间，进而决策自己的出行，其中在计算出行时间时本文同时考虑交通网络的不确定性. 最后运用算例网络测试模型的基本原理和应用价值.

在智慧公路上布设线圈、视频、微波、地磁等交通检测器，同时结合无线通讯和GPS车载定位技术，实时捕捉路段上的交通流量、速度、密度、旅行时间等. 由于数据量纲不一致，运用交通流理论对多源数据类型进行统一化处理. 本研究采用Green Shields交通流量-速度-密度关系^[29]对观测的多源数据进行转换，统一为道路流量：

(1) $ v_a^t = \frac{{{l_a}}}{{{u_a}}}\left[ {{M_{{\rm {j}},a}}\left( {1 - \frac{{{l_a}}}{{{u_a}{S_{{\rm {f}},a}}}}} \right)} \right];\;\; \forall a \in A. $

式中： $A$为路段集， $a \in A$， $t$（ $t = 1,2, \cdots ,n$）为时间变量， $v_a^t$为第 $t$ d路段 $a$上的道路流量， ${l_a}$为路段 $a$的长度， ${u_a}$为路段 $a$上的道路出行时间， ${M_{{\rm {j}},a}}$为路段 $a$上的拥挤密度， ${S_{{\rm {f}},a}}$为路段 $a$上的最大行驶速度. 需要说明的是，如果调查获得的是速度，则将式（1）中的 ${{{l_a}} / {{u_a}}}$替换为速度变量；如果捕捉的是密度，则根据速度密度关系将式（1）中的 ${{{l_a}} / {{u_a}}}$替换为 ${S_{{\rm {f}},a}}\left( {1 - {{{M_a}} / {{M_{{\rm {j}},a}}}}} \right)$，其中 ${M_a}$为密度变量. 路段出行时间可由车辆速度和路段长度推导而得.

通过式（1），将获取的路段速度、密度、旅行时间等变量转换为路段流量，进一步运用最小方差加权平均方法融合统一后的道路流量，其数学表达形式为

(2) $ v_a^t = \sum\limits_{i \in I} {{e_{i,a}}v_{i,a}^t} ;\;\;\forall a \in A. $

式中： $i$为多源观测路段流量类型，如速度、密度、时间等， $i \in I$， ${e_{i,a}}$为路段 $a$上的第 $i$种类型观测路段流量权重系数，

${e_{i,a}} = {\left[ {\sigma _{i,a}^2 \cdot \sum\nolimits_{i \in I} { {{ {\sigma _{i,a}^{-2}}}} } } \right]^{{\rm{ - 1}}}};\;\;\forall i \in I,\;\;a \in A{\rm{.}}$

可知， $\sum\nolimits_{i \in I} {{e_{i,a}}} = 1,\forall a \in A$； $v_{i,a}^t$为路段 $a$上的不同观测数据类型 $i$（如：速度、密度、时间等）统一化后的交通流量；其中 $\sigma _{i,a}^2$为路段 $a$上的第 $i$种类型观测流量的方差，在高峰时刻 $t$（如早高峰8:00—9:00），第 $i$种类型检测器实时捕捉路段 $a$上的交通数据，转换为路段流量后， $\sigma _{i,a}^2$即为该时段内捕捉到的路段流量的方差，可以发现方差越大，权重系数越小. 不同类型的检测器观测数据精度不一样，且无法获知检测数据质量状况，因此使用融合后的数据可以更加全面、客观地反映道路交通状态.

对于实际路网中捕捉的流量、速度、密度、旅行时间等数据，预先无法获知检测数据的精度，因此也无法预知基于单一数据的交通决策效果，而数据融合技术通过对不同来源数据的综合处理，可以有效降低这一不足，同时能弥补部分观测源数据缺失的状况. 本文提出的数据融合方法中对方差大的观测数据类型给予较小的权重系数，一定程度上增加了融合数据的可靠性.

道路容量的退化引起路段和路径出行时间的可变性. 从数学角度来看，路径出行时间 $U_{\omega ,k}^t$是关于路段流量 ${{{v}}^t}$和道路容量 ${{c}}$的随机变量，同时路径出行时间会随着出行者在路径选择时的风险态度 $\alpha $的不同而改变. 式（3）运用可靠出行时间来描述道路网络可变性：

(3) $ \begin{split} & \Pr {\rm{o}}\left( {U_{\omega ,k}^t \leqslant b_{\omega ,k}^t\left( {{{{v}}^t},{{c}},\alpha } \right)} \right) = \alpha ; \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\forall k \in {K_{\omega} },\;\omega \in W,\;t = 1,2, \cdots ,n. \\ \end{split} $

式中： $\Pr {\rm{o}}\left( \cdot \right)$为概率算子， ${{{v}}^t}$为 $v_a^t$的向量形式； ${C_a}$为路段 $a$上的通行能力， ${{c}}$是其向量形式； $W$为交通网络中所有起讫点（origin-destination, OD）对的集合； $\omega $表示其中的一个起讫点， $\omega \in W$； ${K^\omega }$为起讫点 $\omega $之间所有路径的集合， $k \in {K^\omega }$； $U_{\omega ,k}^t$为第 $t$ d 起讫点 $\omega $间路径 $k$上的旅行时间； $b_{\omega ,k}^t\left( \cdot \right)$为第 $t$ d 起讫点 $\omega $间路径 $k$上的可靠出行时间； $\alpha $为出行用户感知的风险态度， $\alpha $越大表明用户认为出行路径中遇到的不确定性越大，反之则表明用户预估出行中的不确定性因素较小.

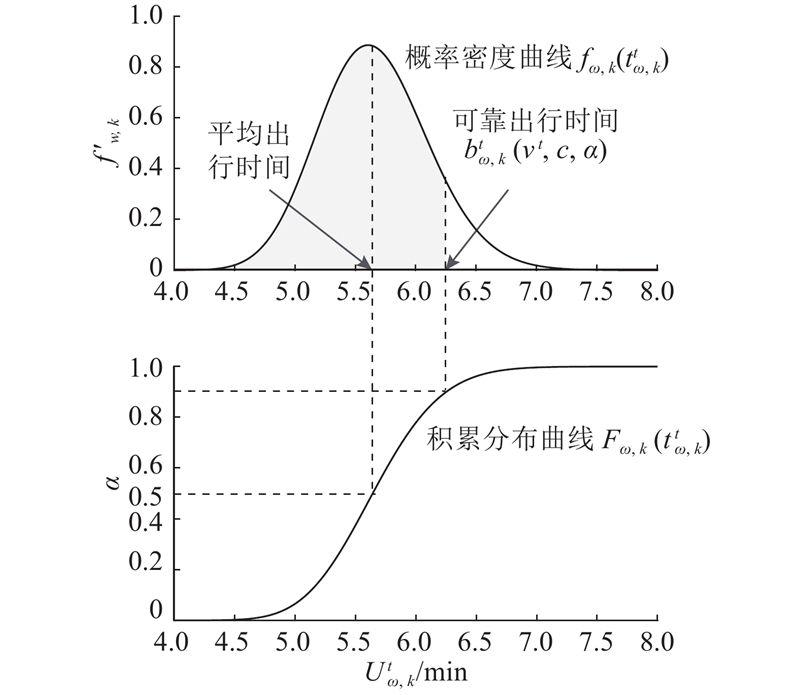
为便于理解可靠出行时间，假定路径出行时间服从参数为1.73和0.08的对数正态分布，图1绘制了出行时间的概率密度和积累分布曲线，可以看出交通参与者在可靠出行时间 $b_{\omega ,k}^t\left( {{{{v}}^t},{{c}},\alpha } \right)$之前到达目的地的概率为 $\alpha $.

根据积累分布函数关系，式（3）等价为

(4) $ \begin{split} & {F_{\omega ,k}}\left( {b_{\omega ,k}^t\left( {{{{v}}^t},{{c}},\alpha } \right)} \right) \!=\!\! \int_0^{b_{\omega ,k}^t\left( {{{\bf{v}}^t},{\bf{c}},\alpha } \right)} {{f_{\omega ,k}}\left( {U_{\omega ,k}^t} \right){\rm d}t_{\omega ,k}^t} \!=\! \alpha ; \\& \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\forall k \in {K_{\omega} },\; \omega \in W. \end{split} $

式中： ${f_{\omega ,k}}\left( \cdot \right)$为起讫点 $\omega $间路径 $k$上可靠出行时间的概率分布函数， ${F_{\omega ,k}}\left( \cdot \right)$为起讫点 $\omega $间路径 $k$上可靠出行时间的积累分布函数.

进一步对式（4）求逆，可得

(5) $ b_{\omega ,k}^t\left( {{{{v}}^t},{{c}},\alpha } \right){\rm{ = }}{F_{\omega ,k}}^{ - 1}\left( \alpha \right);\;\;\forall k \in {K_{\omega} },\;\;\omega \in W. $

式中： ${F_{\omega ,k}}^{ - 1}\left( \cdot \right)$为 ${F_{\omega ,k}}\left( \cdot \right)$的反函数.

在出行过程中，用户倾向于选择可靠出行时间最短的路径完成出行，因此在随机网络交通均衡状态下，没有用户能够通过单方面的路径变更行为，来减小自己的感知可靠出行时间. 换句话说，起讫点间所有使用路径的感知可靠出行时间是相等且最小的. 这与传统的随机用户均衡模型（SUE）的均衡状态是一致的. 对任意 $\omega \in W$，记起讫点 $\omega $间路径 $k$上的出行用户路径选择概率 ${p_{\omega ,k}}\left( {{{b}}_{\omega} ^t\left( {{{{v}}^t},{{c}},\alpha } \right),\theta } \right){\rm{ = }}\Pr {\rm{o}}\left( {{{b}}_{\omega} ^t\left( {{{{v}}^t},{{c}},\alpha } \right),\theta } \right)$，其中 ${{b}}_{\omega} ^t$为 $b_{\omega ,k}^t$的向量形式，随机网络交通均衡状态^[4]为

(6) $ \begin{split} & {p_{\omega ,k}}\left( {{{b}}_{\omega} ^t\left( {{{{v}}^t},{{c}},\alpha } \right),\theta } \right) = \\ & \quad\quad\quad\frac{{\exp \;\left[ { - \theta \cdot b_{\omega ,k}^t\left( {{{{v}}^t},{{c}},\alpha } \right)} \right]}}{{\displaystyle\sum\limits_{k \in {K_{\omega} }} {\exp \;\left[ { - \theta \cdot b_{\omega ,k}^t\left( {{{{v}}^t},{{c}},\alpha } \right)} \right]} }};\forall k \in {K_{\omega} },\omega \in W. \end{split} $

式中： $\theta > 0$为测量道路出行者感知误差程度的离散参数（随机感知误差的方差），用于描述出行者对路网熟悉的程度， $\theta $越大表明出行者对路网越熟悉，反之则表明感知误差较大. 当出行者感知误差服从Gumbel分布时，出行者路径选择概率可以表示为如式（6）所示的指数概率形式. 式（6）描述了在出行过程中，用户选择每条路径的选择概率，其中 $ - \theta \cdot b_{\omega ,k}^t\left( {{{{v}}^t},{{c}},\alpha } \right)$为起讫点 $\omega $间路径 $k$的效用值，其值越高，表明该路径被选择的概率越大. 根据大数定律，路径交通量可表示为

(7) $ {{y}}_{\omega} ^t{\rm{ = }}{q_{\omega} } \cdot {{{p}}_{\omega} }\left( {{{b}}_{\omega} ^t\left( {{{{v}}^t},{{c}},\alpha } \right),\theta } \right);\;\;\forall \omega \in W. $

式中： ${{{p}}_{\omega} }$为 ${{{p}}_{\omega ,k}}$的向量形式， ${q_{\omega} }$为起讫点 $\omega $间的交通需求， $y_{\omega ,k}^t$为第 $t$ d 起讫点 $\omega $间路径 $k$上的交通流量. 其向量形式为

(8) $ {{{y}}^t}{\rm{ = }}{{qp}}\left( {{{{b}}^t}\left( {{{{v}}^t},{{c}},\alpha } \right),\theta } \right). $

式中：q为 ${q_{\omega} }$的向量形式，相应的路段交通量为

(9) $ {{{v}}^t}{\rm{ = }}{{\varLambda}} {{qp}}\left( {{{{b}}^t}\left( {{{{v}}^t},{{c}},\alpha } \right),\theta } \right). $

式中： $\delta _{a,k}^\omega $为路径-路段关联参数，起讫点 $\omega $间，如果路段 $a$在路径 $k$上，该参数为1，否则为0， ${{\varLambda}} $为其矩阵形式.

交通出行通常包含经验学习和路径调整2个过程. 经验学习即在第 $t$ d，出行者无法提前获知每条路径的实际出行时间，因而只能通过以往的出行经验信息来预测当前的路径出行时间；路径调整即在第 $t$ d，出行者根据经验学习的路径出行时间和前一天（第 $t - 1$ d）的出行路径，调整当前（第 $t$ d）的出行路径. 因此，交通出行演化过程是出行者日复一日出行学习的集计体现. 需要说明的是，如果计算第 $t + 1$ d的出行状况，则需要根据前 $t$ d的出行经验.

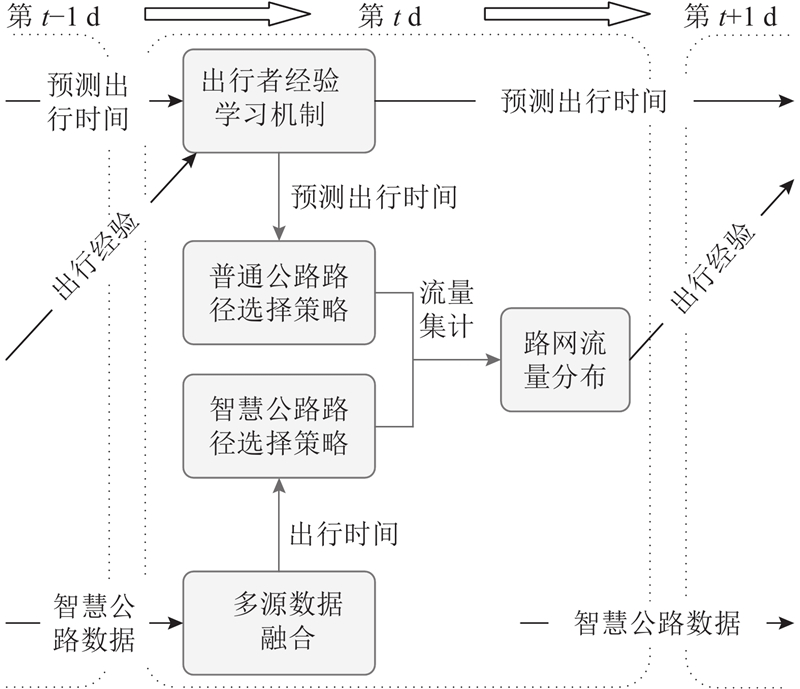
在智慧公路出行演化过程中，智慧公路上的多源数据可以实时提供当前路径信息，因此在智慧公路上行驶的出行者可以提前预知道路状况，而不需要根据历史经验来预测当前路网出行状况. 在路网中同时包含智慧公路和普通公路时，交通出行演化框架如图2所示.

在普通公路上，出行者在第 $t$ d预测的路径可靠出行时间可以表示为第 $t - 1$ d实际可靠出行时间与第 $t - 1$ d预测可靠出行时间的加权和，本文采用指数平滑滤波法来建立普通公路上出行者对出行时间的更新过程：

(10) $ \begin{split} & B_{\omega ,k}^{{\rm{co}},t}{\rm{ = }}\beta \cdot b_{\omega ,k}^{t - 1}\left( {{{{v}}^{t - 1}},{{c}},\alpha } \right) + \left( {1 - \beta } \right) \cdot B_{\omega ,k}^{{\rm{co}},t - 1}; \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\quad\quad\quad\;\forall k \in K_{\omega} ^{{\rm{co}}},\;\;\omega \in W. \end{split} $

式中： $B_{\omega ,k}^{{\rm{co}},t}$为普通公路第 $t$ d 起讫点 $\omega $间路径 $k$上预测的可靠出行时间，其值为第 $t - 1$ d实际可靠出行时间与第 $t - 1$ d预测可靠出行时间的加权和. 因此式（10）的意义如下：出行者在第 $t - 1$ d获得路径实际出行经验信息后，通过对第 $t - 1$ d预测的可靠出行时间进行一定的修正，最终在第 $t$ d得到更新后的路径预测可靠出行时间，用于当天的路径选择和调整. 进一步地，式（10）的向量形式为

(11) $ {{{B}}^{{\rm{co}},t}}{\rm{ = }}\beta {{{b}}^{t - 1}}\left( {{{{v}}^{t - 1}},{{c}},\alpha } \right) + \left( {1 - \beta } \right){{{B}}^{{\rm{co}},t - 1}}. $

式中： $\beta $为出行者在第 $t$ d预测路径出行时间时，对第 $t - 1$ d出行经验的偏好程度，且 $0 \leqslant \beta \leqslant 1$. $\beta $越大表明出行者更相信前一天的出行经验，而较少借鉴历史信息预测的可靠出行时间，反之则表明出行者更愿意接受历史信息预测的可靠出行时间. 一种极端情况是当 $\beta = 1$时， ${{{B}}^{{\rm{co}},t}}{\rm{ = }}{{{b}}^{t - 1}}\left( {{{{v}}^{t - 1}},{{c}},\alpha } \right)$，即出行者直接将前一天的实际可靠出行时间用于预测后一天的路径出行时间.

在智慧公路上，出行者根据智慧公路提供的道路信息，获知智慧公路第 $t$ d 起讫点 $\omega $间路径 $k$上预测的可靠出行时间：

(12) $ B_{\omega ,k}^{{\rm{in}},t}{\rm{ = }}b_{\omega ,k}^t\left( {{{{v}}^t},{{c}},\alpha } \right);\;\;\forall k \in K_{\omega} ^{{\rm{in}}},\;\;\omega \in W. $

其向量形式为

(13) $ {{{B}}^{{\rm{in}},t}}{\rm{ = }}{{{b}}^t}\left( {{{{v}}^t},{{c}},\alpha } \right). $

采用概率型路径选择模型（即式（6））描述出行者的路径调整过程，路径交通流量逐日调整方程如下：

(14) $ \begin{split} & {{y}}_{\omega} ^t{\rm{ = }}\gamma \cdot {q_{\omega} } \cdot {{{p}}_{\omega} }\left( {{{B}}_{\omega} ^{{\rm{co}},t},{{B}}_{\omega} ^{{\rm{in}},t},\theta } \right) + \left( {1 - \gamma } \right) \cdot {{y}}_{\omega} ^{t - 1}; \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\quad\quad\quad\forall \omega \in W. \end{split} $

式中： $\gamma $为出行者路径选择的特征参数， $0 \leqslant \gamma \leqslant 1$， $ {1 - \gamma } $反映了出行者路径选择的惯性程度，其值越大，说明越多的出行者保持原来的路径选择结果；反之，则说明出行者更倾向于根据预测时间信息对路径进行重新选择. 根据路段-路径关联矩阵，推导出路段交通流演化过程：

(15) $ \begin{split} {{{v}}^t}{\rm{ = }} & \gamma \cdot \sum\limits_{\omega \in W} {{q_{\omega} } \cdot {{{\varLambda}} _{\omega} } \cdot {{{p}}_{\omega} }\left( {{{B}}_{\omega} ^{{\rm{co}},t},{{B}}_{\omega} ^{{\rm{in}},t},\theta } \right)} + \\ & \left( {1 - \gamma } \right) \cdot {{{v}}^{t - 1}}. \end{split} $

可知路网流量逐日调整量为

(16) $ \begin{split} {{{v}}^t} - & {{{v}}^{t - 1}}{\rm{ = }} \\ & \gamma \cdot \left( {\sum\limits_{\omega \in W} {{q_{\omega} } \cdot {{{\varLambda}} _{\omega} } \cdot {{{p}}_{\omega} }\left( {{{B}}_{\omega} ^{{\rm{co}},t},{{B}}_{\omega} ^{{\rm{in}},t},\theta } \right) - {{{v}}^{t - 1}}} } \right). \end{split} $

通过整合式（11）、（13）和（15），得到智慧公路多源数据下交通出行演化模型为

(17) $ \left. \begin{array}{l} {{{B}}^{{\rm{co}},t}}{\rm{ = }}\beta {{{b}}^{t - 1}}\left( {{{{v}}^{t - 1}},{{c}},\alpha } \right) + \left( {1 - \beta } \right){{{B}}^{{\rm{co}},t - 1}},\\ {{{B}}^{{\rm{in}},t}}{\rm{ = }}{{{b}}^t}\left( {{{{v}}^t},{{c}},\alpha } \right),\\ {{{v}}^t}{\rm{ = }}\gamma \cdot \sum\limits_{\omega \in W} {{q_\omega } \cdot {{{\varLambda}} _\omega } \cdot {{{p}}_\omega }\left( {{{B}}_\omega ^{{\rm{co}},t},{{B}}_\omega ^{{\rm{in}},t},\theta } \right)} + \left( {1 - \gamma } \right) \cdot {{{v}}^{t - 1}}. \end{array} \right\} $

式中：参数 $\alpha $、 $\beta $、 $\gamma $和 $\theta $均与出行者自身感知相关，通常需要通过实际用户调研获得这些参数值，由于出行者的异质性，这些参数并不是固定值. 本文算例中使用固定值对模型进行测试；对于非固定值，可以采用多用户模型或视参数为随机变量这2种方法解决，将在未来研究中放宽固定值这一假设.

定理1（等价性）如果模型（式（17））的不动点存在，那么该不动点等价于随机路网流量均衡解.

证明：根据不动点动力演化系统^[30]，模型（式（17））的不动点满足条件：

$ \begin{array}{l} {{{B}}^{{\rm{co}},t}} = {{{B}}^{{\rm{co}},t - 1}} = {{{B}}^{{\rm{co}}, * }},\\ {{{B}}^{{\rm{in}},t}} = {{{B}}^{{\rm{in}},t - 1}} = {{{B}}^{{\rm{in}}, * }},\\ {{{v}}^t}{\rm{ = }}{{{v}}^{t - 1}}{\rm{ = }}{{{v}}^ * }. \end{array} $

将上述公式代入模型（式（17））可以得到

$\begin{split} {{{v}}^ * }{\rm{ = }}& \gamma \cdot \displaystyle\sum\limits_{\omega \in W} {{q_{\omega} } \cdot {{{\varLambda}} _{\omega} } \cdot {{{p}}_{\omega} }\left( {{{B}}_{\omega} ^{{\rm{co}}, * },{{B}}_{\omega} ^{{\rm{in}}, * },\theta } \right)} + \left( {1 - \gamma } \right) \cdot {{{v}}^ * } \Rightarrow \\& \displaystyle\sum\limits_{\omega \in W} {{q_{\omega} } \cdot {{{\varLambda}} _{\omega} } \cdot {{{p}}_{\omega} }\left( {{{B}}_{\omega} ^{{\rm{co}}, * },{{B}}_{\omega} ^{{\rm{in}}, * },\theta } \right)} = {{{v}}^ * }. \end{split} $

这刚好符合SUE均衡条件^[4]，因此定理1得证.

为研究模型解的存在性、唯一性和稳定性，给出路径出行时间函数和路径选择概率的数学假设.

假设1：路径可靠出行时间 ${{b}}\left( {{{{v}}^t},{{c}},\alpha } \right)$关于路径流量 ${{{y}}^t}$连续.

假设2：路径选择概率 ${{p}}\left( {{{{B}}^{{\rm{co}},t}},{{{B}}^{{\rm{in}},t}},\theta } \right)$分别关于普通公路预测可靠出行时间 ${{{B}}^{{\rm{co}},t}}$和智慧公路预测可靠出行时间 ${{{B}}^{{\rm{in}},t}}$连续.

在交通网络理论中，路段流量为经过该路段的所有路径流量和，路段出行时间为路段流量的连续函数，路径出行时间关于路段出行时间连续，因此路径出行时间也关于路径流量连续. 进一步根据式（5）得， ${F_{\omega ,k}}^{ - 1}\left( \alpha \right)$关于路径流量连续，即可靠出行时间 ${{b}}\left( {{{{v}}^t},{{c}},\alpha } \right)$关于路径流量 ${{{y}}^t}$连续，因此通常实际路网满足假设（1）和（2）中的条件.

定理2模型（式（17））存在均衡解.

证明：根据布劳威尔不动点定理^[30]，从一个欧几里得空间的某个闭凸子集到其自身的连续映射至少存在一个不动点. 由于交通需求 ${q_{\omega} \geqslant 0}$且存在上限界，从而路径流量和路段流量的可行集也都非负且存在上限界，路径流量和路段流量的可行集都属于有界闭凸集. 在交通模型中，每个起讫点间至少存在1条可行路径，因此路径流量和路段流量可行集非空. 进一步根据假设（1）和（2），可知式（17）定义的路段流量自我映射关系满足连续性条件，因此满足布劳威尔不动点定理要求. 模型解即不动点的存在性得证.

如果路径可靠出行时间关于路径流量单调递增，且路径选择概率关于预测可靠出行时间单调递减，那么模型解唯一. 通常路径阻抗与路径流量之间关系复杂，路径阻抗并不一定是路径流量的单调递增函数，因此模型（式（17））解的唯一性并不能得到保证.

为研究模型（式（17））解的稳定性，根据非线性离散动力系统理论，将演化模型（式（17））表示成如下离散动力系统形式：

(18) $ \left( {{{{B}}^{{\rm{co}},t}},{{{B}}^{{\rm{in}},t}},{{{v}}^t}} \right){\rm{ = }}\varphi \left( {{{{B}}^{{\rm{co}},t - 1}},{{{B}}^{{\rm{in}},t - 1}},{{{v}}^{t - 1}}} \right). $

由于 ${{{B}}^{{\rm{in}},t}}$与 $\left( {{{{B}}^{{\rm{co}},t - 1}},{{{B}}^{{\rm{in}},t - 1}},{{{v}}^{t - 1}}} \right)$无关，式（18）简化为

(19) $ \left( {{{{B}}^{{\rm{co}},t}},{{{v}}^t}} \right){\rm{ = }}\varphi \left( {{{{B}}^{{\rm{co}},t - 1}},{{{v}}^{t - 1}}} \right). $

式中： $\varphi \left( \cdot \right)$为演化模型（式（17））中的状态转移函数关系. 用 ${{{J}}^ * }$表示转移函数 $\varphi \left( \cdot \right)$的雅可比矩阵，用 ${{{J}}_{{b}}}^ * $表示 ${{{b}}^{t - 1}}\left( {{{{v}}^{t - 1}},{{c}},\alpha } \right)$关于 ${{{v}}^{t - 1}}$的雅可比矩阵，用 ${{{J}}_{{p}}}^ * $表示 ${{p}}\left( {{{{B}}^{{\rm{co}},t}},{{{B}}^{{\rm{in}},t}},\theta } \right)$关于 ${{{B}}^{{\rm{co}},t}}$的雅可比矩阵，根据矩阵代数运算得到

(20) $ {{{J}}^ * } = \left[ {\begin{array}{*{20}{c}} {\left( {1 - \beta } \right){{I}}}&{\beta {{{J}}_{{b}}}^ * } \\ {\left( {1 - \beta } \right)\gamma {{\varLambda}} {{q}}{{{J}}_{{p}}}^ * }&{\left( {1 - \gamma } \right){{I}}' + \beta \gamma {{\varLambda}} {{q}}{{{J}}_{{p}}}^ * {{{J}}_{{b}}}^ * } \end{array}} \right]. $

式中： ${{I}}$和 ${{I}}'$为单位矩阵.

根据不动点稳定性条件^[30]，当且仅当雅克比矩阵（式（20））的所有特征值都在单位圆内，演化模型（式（17））是稳定的. 由式（式（20））可知，出行者出行经验偏好程度 $\beta $和路径选择特征 $\gamma $影响模型的稳定性，而 $\beta $和 $\gamma $的取值与出行者感知和选择特性相关，因此并不能保证模型（式（17））解的稳定性，下文将通过算例分析特定模型下解的稳定区域.

采用通常使用的美国联邦公路局路段特性函数^[31]来描述路段阻抗：

(21) $ {u_a}\left( {v_a^t,{C_a}} \right) = u_a^{{\rm{free}}} \cdot \left[ {1 + m{{\left( {\frac{{v_a^t}}{{{C_a}}}} \right)}^n}} \right];\;\;\forall a \in A. $

式中： $u_a^{{\rm{free}}}$为路段 $a$上的自由旅行时间； $m$和 $n$为路段特性函数中的参数， $m = 0.15$、 $n = 4$.

根据文献[6]，道路容量服从 ${C_a} \sim {\rm{Uniform}}\left( {{\lambda _a}{{\bar c}_a},{{\bar c}_a}} \right)$均匀分布，其中 ${\bar c_a}$为路段 $a$上的容量上界，则路段出行时间的均值和方差分别为

(22) $\begin{split} E\left( {{u_a}\left( {v_a^t,{C_a}} \right)} \right) = & u_a^{{\rm{free}}} + mu_a^{{\rm{free}}}{\left( {v_a^t} \right)^n}\frac{{ {1 - \lambda _a^{1 - n}} }}{{\bar c_a^n\left( {1 - {\lambda _a}} \right)\left( {1 - n} \right)}}, \\ & \forall a \in A;\\[-9pt] \end{split}$

(23) $\begin{split} & {\rm{var}} \left( {{u_a}\left( {v_a^t,{C_a}} \right)} \right) = {m^2}{\left( {u_a^{{\rm{free}}}} \right)^2}{\left( {v_a^t} \right)^{2n}} \\ & \quad\left\{ {\frac{{\left( {1 - \lambda _a^{1 - 2n}} \right)}}{{\bar c_a^{2n}\left( {1 - {\lambda _a}} \right)\left( {1 - 2n} \right)}} - {{\left[ {\frac{{\left( {1 - \lambda _a^{1 - n}} \right)}}{{\bar c_a^n\left( {1 - {\lambda _a}} \right)\left( {1 - n} \right)}}} \right]}^2}} \right\},\forall a \in A. \end{split}$

式中： ${\lambda _a}$为路段 $a$上的容量上界与下界的比例系数.

在路段通行能力和出行时间相互独立的情况下，进一步推导出路径出行时间的均值和方差分别为

(24) $ \begin{split} E\left( {U_{\omega ,k}^t} \right) = & \displaystyle\sum\limits_a {\left[ {{\delta _{a,\omega ,k}}E\left( {{u_a}\left( {v_a^t,{C_a}} \right)} \right)} \right]} , \\& \quad\quad\quad\forall k \in {K_{\omega} },\omega \in W; \end{split} $

(25) $ \begin{split} {\rm{var}} \left( {U_{\omega ,k}^t} \right) =& \displaystyle\sum\limits_a {\left[ {{\delta _{a,\omega ,k}}{\rm{var}} \left( {{u_a}\left( {v_a^t,{C_a}} \right)} \right)} \right]} , \\ & \forall k \in {K_{\omega} },\omega \in W. \end{split} $

由于路径出行时间为多条路段出行时间的和，根据中心极限定理可得路径出行时间近似服从多元正态分布形式

(26) $ \begin{split} U_{\omega ,k}^t \sim &N\left( {{{E}}\left( {U_{\omega ,k}^t} \right),{\rm{var}} \left( {U_{\omega ,k}^t} \right)} \right); \\ &\quad\quad\quad\forall k \in {K_{\omega} },\omega \in W. \end{split} $

进一步根据式（5）推导出可靠出行时间为

(27) $ \begin{split} &b_{\omega ,k}^t\left( {{{{v}}^t},{{c}},\alpha } \right) = {{E}}\left( {U_{\omega ,k}^t} \right) + \\ & \qquad {\varPhi ^{{\rm{ - }}1}}\left( \alpha \right) \cdot \left[ {{\rm{var}} \left( {U_{\omega ,k}^t} \right)}\right]^{1/2} ;\;\;\forall k \in {K_{\omega} },\;\;\omega \in W. \end{split} $

式中： ${\varPhi ^{{\rm{ - }}1}}(\alpha )$为标准正态分布的累计分布函数在置信水平 $\alpha $处的值.

本章分别运用一个小网络和Nguyen-Dupuis网络^[32]描述建立模型的基本思想和应用性.

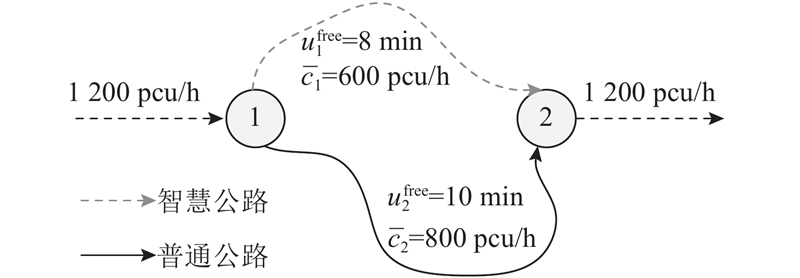
图3给出了测试网络拓扑结构和路段属性，该网络由2个结点、2个路段（1条智慧公路和1条普通公路）和1个起讫点组成. 其中高峰小时OD交通量为1 200 pcu/h，智慧公路的自由旅行时间和道路容量上界分别为8 min和600 pcu/h，普通公路的自由旅行时间和道路容量上界分别为10 min和800 pcu/h.

假设道路网初始流量状态为 $\left( {v_1^0,v_2^0} \right) =$ $ \left( {300,\;900} \right) $，运用数据融合方法，即根据式（1）、（2）实时获取智慧公路流量信息，将路段容量上界与下界的比例系数设为 ${\lambda _1} = {\lambda _2} = 0.8$，将出行者的风险态度设为 $\alpha = 0.8$. 在道路出行者感知误差程度 $\theta = 1$的情况下，测试出行者在4类不同行为参数（ $\beta $和 $\gamma $）组合下2条路段的交通量逐日演化过程，如图4所示. 可以看出，图4（a）~（c）分别在经过10、30和5 d的流量波动后最终收敛到唯一的不动点，而图4（d）不满足不动点稳定性条件，因此交通流量一直在震荡. 通过比较发现，较大的出行时间行为系数 $\beta $有利于增加模型演化到均衡状态的速度，达到交通均衡状态的速度，而较大的道路流量行为系数 $\gamma $会导致动态演化模型进入不稳定状态. 进一步在不同 $\beta $和 $\gamma $值下进行测试发现：当 $\gamma \leqslant 0.26$时，无论 $\beta $的取值如何，模型解均收敛；当 $\gamma \geqslant 0.33$时，无论 $\beta $的取值如何，模型解均不能收敛至稳定点；而当 $0.26 < \gamma < 0.33$时，随着 $\beta $值的增大，模型解的稳定性降低.

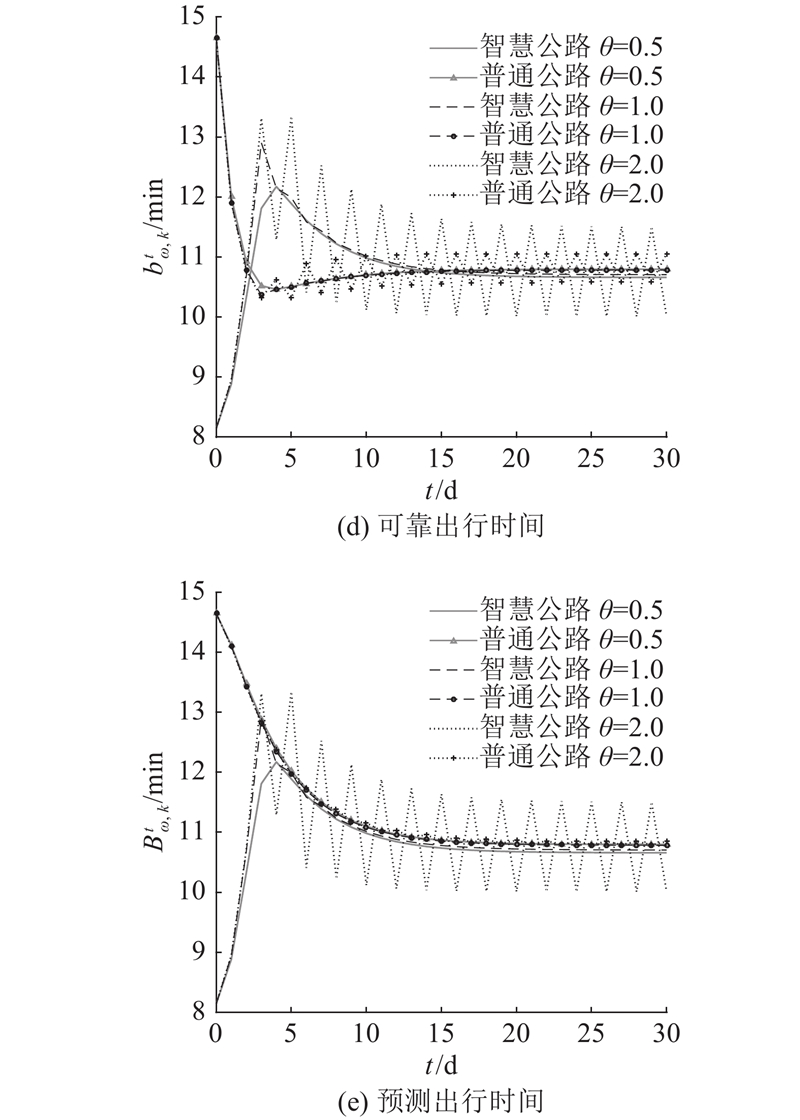
进一步测试出行者感知时间误差 $\theta $对动态演化模型的敏感程度，如图5所示，其中将出行者行为参数分别设为 $\beta = 0.2$和 $\gamma = 0.2$. 图中显示，随着感知时间误差 $\theta $的增大，路网交通流量演化过程逐渐从稳定状态变为不稳定状态. 图4同时可以说明模型的基本思想，在感知时间误差 $\theta $=0.5时，在稳定状态下，智慧公路的交通量、出行时间均值、方差和预测出行时间分别为621 ${\rm{pcu/h}}$、10.19 $\min $、0.318 ${\min ^2}$和10.66 $\min $；普通公路的交通量、出行时间均值、方差和预测出行时间分别为579 ${\rm{pcu/h}}$、10.66 $\min $、0.029 ${\min ^2}$和10.80 $\min $. 智慧公路的可靠出行时间为

$b_1^{30} = E\left( {U_1^{30}} \right) + {\varPhi ^{{\rm{ - }}1}}\left( \alpha \right) \cdot \left[ {{\rm{var}} \left( {U_1^{30}} \right)}\right]^{1/2} = 10.66 \;\min ,$

同样普通公路可靠出行时间为 $b_2^{30} = 10.80 \;\min $，在均衡状态下，普通公路的出行经验和预测出行时间是相等的，因此普通公路在第30 d预测的可靠出行时间为 $10.80 \;\min $，智慧公路上的路径选择概率为

${p_1} = {{\exp \left[ { - \theta \cdot b_1^{30}} \right]} \Big/ {\sum\nolimits_{k = 1,2} {\exp \left[ { - \theta \cdot b_k^{30}} \right]} }} = 0.517\;5.$

同样普通公路上路径选择概率为 ${p_2} = 0.482\;5$，因此智慧公路上的交通流量为 $v_1^{30} = {p_1} \cdot q = 621\;{\rm{pcu/h}}$，普通公路上的流量为 $v_2^{30} = 579\;{\rm{pcu/h}}$，这与图5中的收敛结果一致.

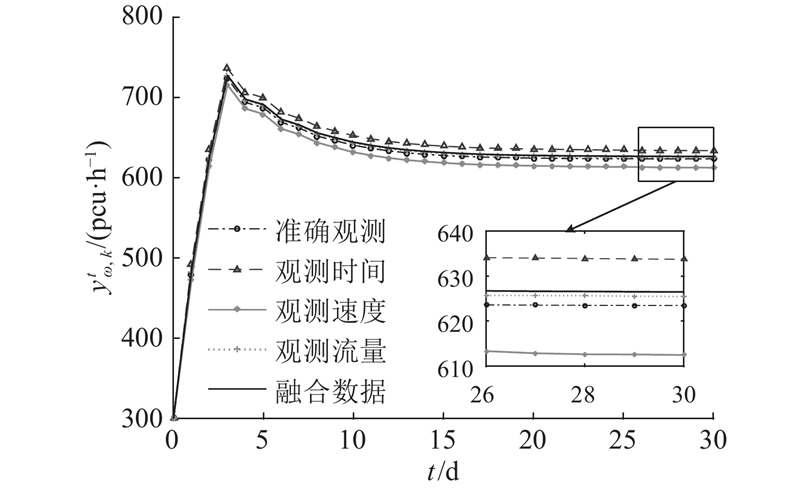
在上述算例测试中，智慧公路上的数据均采用前一天出行均衡后的路段流量来计算当前可靠出行时间值，图6描绘了多源和单源观测数据下智慧路段流量演化规律. 智慧公路长度、拥挤密度和最大行驶速度分别为8 km、40 pcu/km和60 km/h. 实验时分别单独观测路段旅行时间、行程速度和路段流量3个变量，为了检测多源数据融合的效果，分别给予这3个观测变量一定的扰动：−1%、2%和0.5%，其余参数与图4（a）测试参数保持一致. 从图6中可以看出，当检测数据存在扰动时，模型估计出来的路段流量也会产出误差；同时数据融合后推断的最优解虽然不如部分单源数据（观测流量存在0.5%的误差）估计的流量值精度高，但使用融合数据不会出现估计结果误差过大的情况，比如单纯使用路段旅行时间和行程速度估计的路段流量误差过大. 在实际网络规划过程中，无法获知检测数据的精度高低，因此数据融合方法是一种折中的方法. 在最小方差加权平均方法融合（式（2））中，方差越大，权重系数越小，因此这种折中方法更倾向于选择稳定性高的数据，并且使用融合数据进行交通流量演化更具鲁棒性. 同时当部分检测器数据存在缺失时，融合数据更能显示其优越性.

Nguyen-Dupuis网络由13个结点、4个起讫点和19条路段组成. 网络的拓扑结构、路段属性和交通需求量如图7所示. 网络中路段5-6、6-7和6-10为智慧路段，将路段容量上界与下界的比例系数设为 $\lambda = 0.7$，将出行者的风险态度设为 $\alpha = 0.8$. 部分路径同时包含普通路段和智慧路段，在计算这部分路径可靠出行时间时，分别计算普通路段和智慧路段出行时间均值和方差，进而分别计算出由普通路段和智慧路段组成的子路径可靠出行时间，取其和作为该路径的可靠出行时间. 举例来说，在路径1-5-6-7-11-2中，路段5-6和6-7为智慧路段，本算例将5-6-7作为智慧子路径，1-5和7-11-2作为普通子路径，进而分别计算出这两部分子路径的可靠出行时间，其和即为路径1-5-6-7-11-2的可靠出行时间.

在道路出行者感知误差程度 $\theta = 1$且风险态度 $\alpha = 0.8$的情况下，根据不同的 $\beta $和 $\gamma $参数组合，比较相应的路网流量演化过程. 图8比较了3种不同的 $\beta $和 $\gamma $参数组合下，前、后2天路段流量的偏差程度 ${H^t}$的变化过程. 评价指标 ${H^t}$的定义如下：

(28) $ {H^t} = {\left\| {{{{v}}^t} - {{{v}}^{t - 1}}} \right\|^2}. $

可以看出，当 $\left( {\beta ,\gamma } \right) = \left( {0.7,0.3} \right)$时，评价指标 ${H^t}$在前50 d呈现波动并收敛到0.001，表明路网交通流量收敛到唯一的不动点状态；同样在 $\left( {\beta ,\gamma } \right) = \left( {0.3,0.3} \right)$时，路网交通流量可以收敛到最优点；而当 $\gamma $增加到0.4时，评价指标 ${H^t}$一直保持震荡过程，说明这种情况下交通流量演化过程是不稳定的. 这与图4显示的结果一致，即较大的参数 $\gamma $会导致网络交通流量进入不稳定状态.

进一步研究智慧公路数量分别增加到4、5、6、7对模型解的影响状况. 经过测试发现，智慧公路数量的增加对模型收敛解没有显著影响，但随着智慧公路数量的增加，模型收敛速度增快，其中当智慧公路数量4、5、6、7条时收敛天数分别为45、41、38和37.

出行者风险态度 $\alpha $对模型解的影响状况如图9所示，在风险态度分别为0.8和0.6的条件下，组合不同行为参数（ $\beta $和 $\gamma $），进而对建立的模型流量进行动态演化. 从图中可以发现，考虑风险规避行为出行演化模型解的稳定区域小于考虑风险倾向行为出行演化模型解的稳定区域；出行时间行为系数 $\beta $的大小对模型稳定性的影响较小，而道路流量行为系数 $\gamma $的大小对模型稳定性产生显著影响. 当出行者风险态度为0.8时，模型解收敛条件为 $\gamma \leqslant 0.25$，发散条件为 $\gamma \geqslant 0.4$；当风险态度为0.6时，模型解收敛条件为 $\gamma \leqslant 0.35$，发散条件为 $\gamma \geqslant 0.5$.

根据第2.3节可知，建立的出行演化模型（式（17））解的唯一性并不能得到保证，因为路径阻抗不一定是路径流量的单调递增函数. 第2.4节中的可靠路径时间建模采用文献[6]中道路容量服从均匀分布这一路网不确定性因素，此时路段出行时间均值和方差均关于路段流量 $v_a^t$单调递增（式（22）、（23）），从而路径流量均值方差也关于路段流量单调递增（式（24）、（25））. 同时路段流量为经过该路段的所有路径流量和，因此在道路容量存在不确定性时，路径可靠出行时间是路径流量的单调递增函数（式（27）），即本算例模型收敛到唯一均衡解. 但当交通需求存在不确定性或交通需求存在弹性时，模型解的收敛状况与初始值和收敛算法相关.

（1）本研究运用交通流理论对智慧公路获取的多源数据进行转化，从而统一观测变量为路段流量，进一步采用最小方差加权平均方法融合路段流量信息. 提出了智慧公路多源数据下的交通出行演化模型，在考虑交通网络不确定性的基础上，该模型假定智慧公路上的出行者根据实时信息进行路径选择，普通公路上的出行者根据历史出行经验和前一天的出行时间信息来决策当日出行策略. 采用不动点理论证明了模型解的等价性、存在性、唯一性和稳定性条件.

（2）通过算例测试了建立演化模型的性能，结果表明：出行时间行为系数的增大会增加模型收敛速度，而道路流量行为系数的增大会导致模型进入不稳定状态. 在本文小网络算例中，当 $\gamma \leqslant 0.26$时，无论 $\beta $的取值如何，模型解均收敛；当 $\gamma \geqslant 0.33$时，无论 $\beta $的取值如何，模型解均不能收敛至稳定点；而当 $0.26 < \gamma < 0.33$时，随着 $\beta $值的增大，模型解的稳定性降低；在Nguyen-Dupuis网络中，当出行者风险态度为0.8时，模型解收敛条件为 $\gamma \leqslant 0.25$，发散条件为 $\gamma \geqslant 0.4$；当风险态度为0.6时，模型解收敛条件为 $\gamma \leqslant 0.35$，发散条件为 $\gamma \geqslant 0.5$；感知时间误差的增大也会降低模型的收敛性；稳定状态的模型解满足不确定网络下的SUE均衡条件，且路段流量偏差程度能够快速收敛到0.001的精度；风险规避的出行者演化模型稳定区域往往更小.

后续将进行连续型交通出行演化研究，并进一步将建立的演化模型应用到实际网络中.