光电容积描记术（photoplethysmography，PPG）是非侵入性光学方法，用于检测微血管组织中血容量的变化^[1-2]. 测量原理是光与生物组织的有效相互作用，包括多重散射、吸收、反射、透射的光学过程. 对于PPG信号的生理学起源目前仍有争论，主要可以概括为3种理论模型：1）早期的研究共识是，心脏搏动引起动脉血管中血容量变化，导致透过生物组织的光强度发生变化^[3]；2）Kamshilin等^[4]提出PPG信号周期性变化的来源是动脉压力的脉动振荡使真皮结缔组织变形引起毛细血管血体积流量变化从而导致光散射和吸收的周期性变化；3）Volkov等^[5]最近提出，PPG波形实质来源于毛细血管中红细胞的迁移速度和相位变化. 尽管对于PPG波形的生理起源，尚未达成统一共识，但这3种理论模型都强调PPG信号与血液流变信息的高度相关性，包括血管血容量、血管壁振荡和红细胞的方位^[6-8]. 在实际测量中PPG信号的动力成分是复杂的，波形中包含丰富的生理信息，如心率调节^[9]、血压调节^[10]、呼吸调节^[11]、神经调节^[12]和其他噪音. 如何从PPG信号中剥离出实质表征血液流变信息的动力组分是推广这种技术在医学和其他研究实践中广泛应用的关键.

目前PPG信号的理论研究主要集中在2个领域，一部分是提取其形态和传输特征参数进行差异性统计分析，这一部分研究已较为成熟；另一部分为信号的频域分析，这一部分研究相对较少. 在频域分析中，大部分研究集中在使用傅里叶变换分解PPG信号^[13-15]，但傅里叶分析仅将数据显示为一系列固定振幅的正、余弦函数，不能反映实际测量中每个采样点上波的活动强度. PPG信号是表达人体生理信息的非稳态非线性信号，应使用非线性动力学方法进行分析.

因此，本研究采用希尔伯特黄变换（Hilbert-Huang transform，HHT）对PPG信号进行分解，考察人体PPG信号频域特征，寻找信号中实际表征血液流变信息的动力成分. 设计低氧实验，分析由低氧诱导的人体血液流变变化信息在PPG信号中的变化趋势.

从北京科技大学招募30名健康青年大学生（男性、女性各15名；年龄为22.7±3.7岁）. 受试者均无神经或心血管疾病史，无吸烟习惯，实验前10 d无药物使用. 实验方案得到北京大学生物医学伦理委员会批准（批准号为IRB00001052-18077），并按照赫尔辛基宣言所阐述的道德标准进行. 将实验方案于实验前告知所有受试者，并在受试者同意后进行实验.

实验在北京科技大学自主研发的矿用可移动式救生舱中进行，实验场景布置如图1（a）所示，实验真实场景如图1（b）所示.

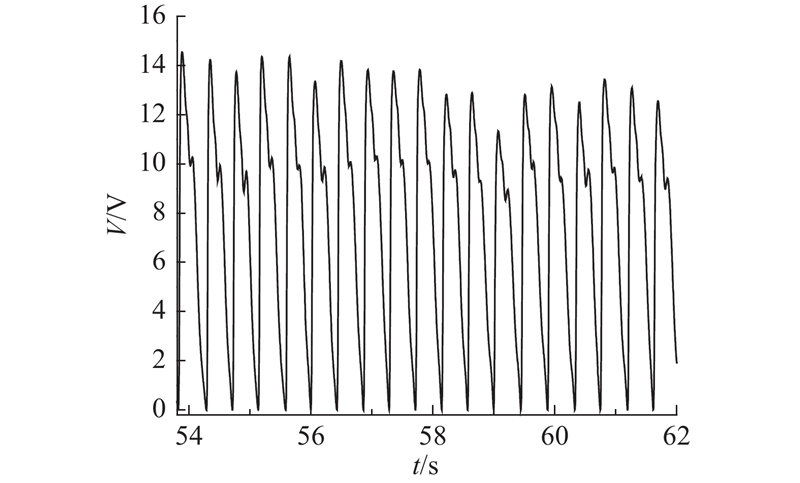
PPG数据采集使用透射式商业测量装置（DHD-6000），采样频率为500 Hz，装置光源由发射780、850 nm波长的双波长激光二极管组成，可穿透皮肤组织深度2.5 mm，采集装置如图2所示. 考虑到受试者皮肤色素沉着、皮肤厚度差异等生物因素，针对每个受试者单独校准检验器增益，保证信号强度最大化.

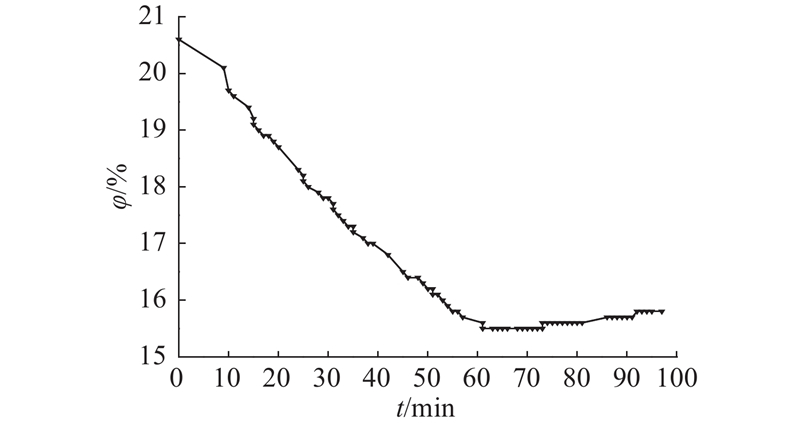
所有受试者经历相同的实验方案. 环境温度过低可能导致周围血管收缩而引起实验误差，故在实验开始之前要求受试者以仰卧姿势在环境温度为26±1 °C的房间内休息30 min，待血液动力学参数稳定后再进入实验舱. 在受试者进舱后，立即关闭舱门，测量此时右手食指指端PPG连续信号7 min，获得超过400个PPG完整波形，测量全程要求受试者完全静息，测量数据记录为正常氧气体积分数情况下PPG信号数据. 在第1次测量结束后，通过放置在舱内的压缩气瓶缓慢向舱内释放氮气（N₂），通过无线气体浓度监测传感器监测舱内氧气体积分数的变化. 待舱内氧气体积分数降至15%~16%时，再次测量受试者PPG信号，一般选择在氧气体积分数约为15.5%时开始测量，采集连续PPG信号7 min，记录为极端低氧情况下PPG信号数据. 同时记录所有受试者在不同氧气体积分数条件下的心率（受试者数量较多，故取所有受试者心率的平均值），如表1所示. 对2种氧气体积分数条件下受试者的心率做独立样本t检验，确认在2种氧气体积分数条件下受试者心率存在显著性差异（P<0.05）. 通过控制N₂释放速度，保证在每次实验中氧气体积分数的下降速率基本一致，一般情况下舱内氧气体积分数变化情况如图3所示. 图中，φ为氧气体积分数.

数据处理与分析均使用MATLAB（R2016b，USA）实现. 首先以Elgendi^[16]所阐述的劣质信号辨别原则手动切除原始信号中明显的劣质信号和运动伪迹成分. 使用于露等^[17]所述PPG信号处理方法对实验获得的PPG信号进行基线漂移、去噪、平滑预处理，预处理后信号质量较好，如图4所示. 图中，V为信号振幅. 采用HHT对预处理后的PPG信号进行进一步的处理分析.

HHT是非线性非平稳时间序列信号处理方法，主要包括2个步骤，经验模式分解（empirical mode decomposition，EMD）和Hilbert变换^[18]. EMD的实质是对时间序列信号进行平稳化处理^[19]，将信号中不同尺度的波动或趋势逐级分解，获得具有不同特征尺度的数据系列，这些系列称为固有模态函数（intrinsic mode function，IMF）^[20]，每个IMF都是单动力模式信号^[21]. 基于这些IMF分量进行Hilbert变换后得到的结果能够反映真实的物理、生理过程^[22].

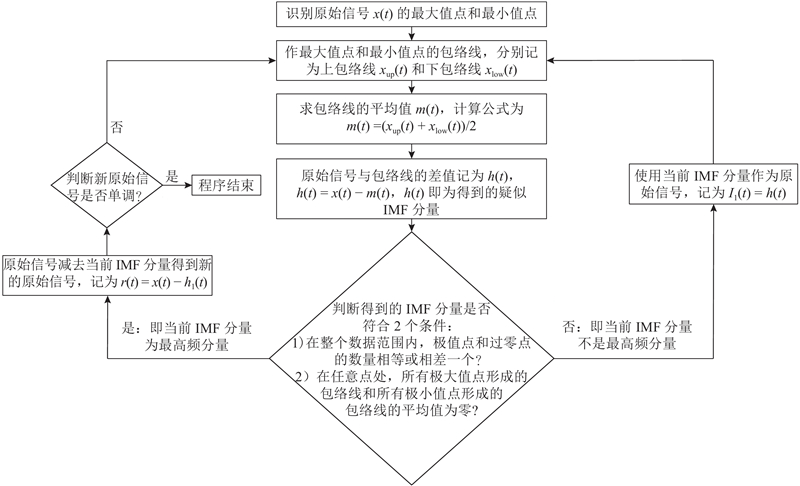
经验模式分解过程即筛选过程，实现振动模式的提取. EMD的基本思路是用信号上、下包络的平均值去确定“瞬时平衡位置”，进而提取出固有模态函数. 上、下包络线是由三次样条函数对极大值点和极小值点进行拟合得到的. EMD的算法思路如图5所示. 图中， $x\left( t \right)$表达式可以写成 $x\left( t \right) = \displaystyle\sum\nolimits_{i = 1}^n {{h_i}\left( t \right){\rm{ + }}r\left( t \right)} $，即原始信号是由n个固有模态函数h_i(t)与1个趋势项r(t)组成的.

在完成经验模式分解过程后就得到所有可提取的固有模态函数，根据Hilbert变换公式（式（1）~（4））可求得瞬时频率. 任何信号 $x\left( t \right)$的Hilbert变换定义如下：

(1) $H\left[ {x\left( t \right)} \right] = y\left( t \right) = \frac{1}{{\text{π}} }{\rm{PV}} {\int_{ - \infty }^\infty {\frac{{x\left( \tau \right)}}{{t - \tau }}} {\rm d}\tau } .$

式中：PV为柯西主值， $y\left( t \right)$为 $x\left( t \right)$的Hilbert变换式. 式（1）表示 $y\left( t \right)$是 $x\left( t \right)$与 ${1 / {\left( {{\text{π}} t} \right)}}$的卷积.

$x\left( t \right)$、 $y\left( t \right)$组成共轭复数对，可以得到解析信号 $z\left( t \right)$，因此，任何解析信号 $z\left( t \right)$都可以用其实部 $x\left( t \right)$和虚部 $y\left( t \right)$之和来表示，即

(2) $z\left( t \right) = x\left( t \right) + {\rm i}y\left( t \right).$

可在极坐标中重写式（2）：

(3) $z\left( t \right) = \alpha \left( t \right){{\rm e}^{{\rm i}\theta \left( t \right)}}.$

式中：

(4) $ \left. \begin{array}{l} \alpha \left( t \right) = {\left( {{x^2}\left( t \right) + {y^2}\left( t \right)} \right)^{1/2}},\\ \theta \left( t \right) = {\tan ^{ - 1}}\;\left( {{{y\left( t \right)} / {x\left( t \right)}}} \right). \end{array} \right\} $

其中， $\alpha \left( t \right)$、 $\theta \left( t \right)$分别为解析信号的瞬时频率和相位.

从瞬时相位可以导出瞬时频率：

(5) $\omega \left( t \right) = {{{\rm d}\theta \left( t \right)} / {{\rm d}t}}.$

在对固有模式函数进行Hilbert转换后，信号表达式如下：

(6) $x\left( t \right) = \operatorname{Re} \left\{ {z\left( t \right)} \right\} = \operatorname{Re} \sum\nolimits_{i = 1}^n {\alpha \left( t \right){{\rm e}^{{\rm i}\theta \left( t \right)}}}. $

式中： $\operatorname{Re} \left\{ {z\left( t \right)} \right\}$为解析信号 $z\left( t \right)$的实部.

为了确保从式（5）中获得的瞬时频率具有物理意义，瞬时相位必须是单调函数. 由Hilbert变换得出的振幅和频率都是时间的函数，如果用三维图形表达幅值、频率和时间之间的关系，就可以得到Hilbert谱，表达式如下：

(7) $H\left( {\omega ,t} \right) = \operatorname{Re} \sum\nolimits_{i = 1}^n {\alpha \left( t \right){{\rm e}^{{\rm i}\int {\omega \left( t \right){\rm d} t} }}} .$

对时间积分，就得到希尔伯特边际谱，表达式如下：

(8) $h\left( \omega \right) = \int_0^t {H\left( {\omega ,t} \right){\rm d}t} .$

Hilbert边际谱提供对每个瞬时频率的总振幅的量测，表达整个时间长度内累积的振幅.

PPG信号经EMD分解得到一系列固有模态函数分量，表征不同的生理活动信息. 如图6所示为一位受试者在低氧环境中的PPG信号EMD分解情况. 可以看出，IMF₇是具有明显可辨别的类似动脉收缩舒张波形^[23]的周期性振荡的固有模态函数，符合本研究所寻找的血液流变特性的评估依据.

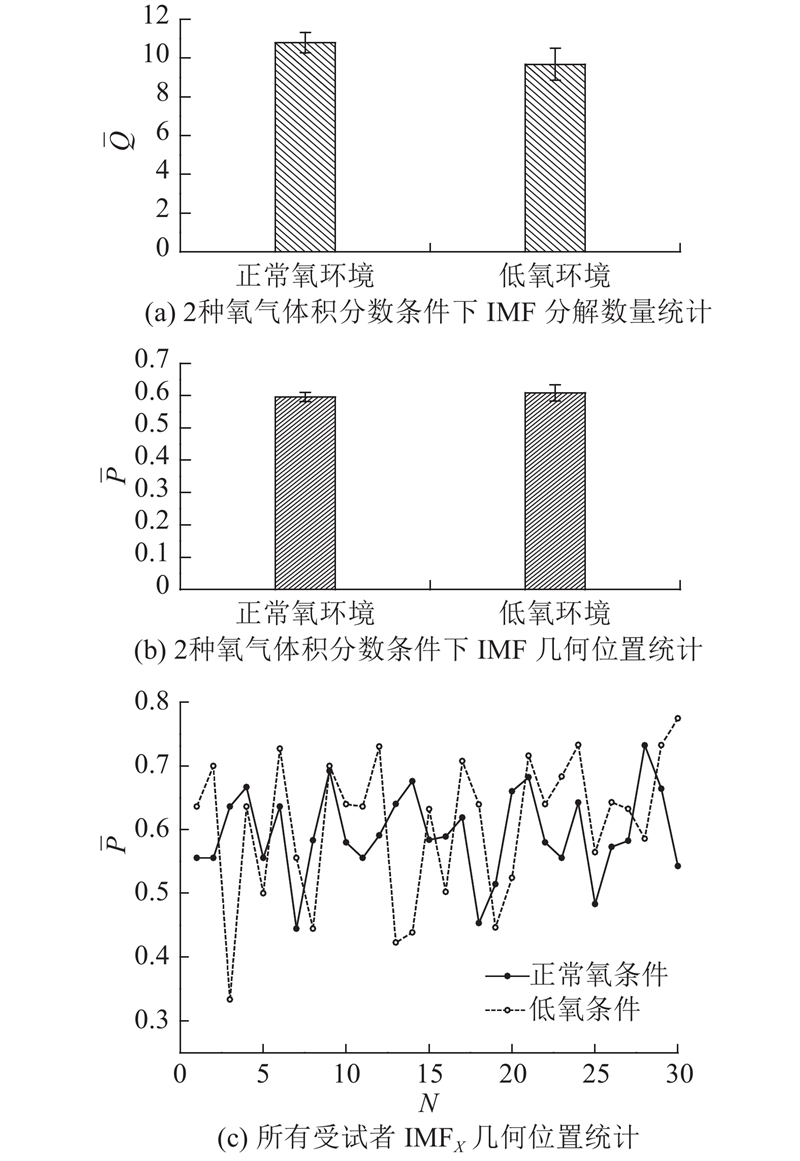
Wu等^[24-25]认为桡动脉处PPG信号经EMD分解得到的IMF₅是表征血液流变特性的实际生理动力成分，并认为该IMF的序号是固定的，为IMF₅. 本研究分解得到的IMF₇与文献中的IMF₅具有类似的形状和周期振荡性质，但IMF序号不一致. 为了探究这种差异产生的原因，定义PPG信号中可表征血液流变特性的实际动力组分为IMF_X. 对所有受试者在正常氧和低氧2种条件下的PPG信号进行EMD分解，并对IMF分解数量进行统计分析，统计结果如图7（a）所示. 图中， $\bar Q $为分解得到的IMF数量的平均值. 结果表明，虽然在趋势上表现为正常氧体积分数环境下分解得到的IMF数量多于低氧环境下的，但差异在统计学上并不显著（经独立样本t检验，P>0.05），且在不同受试者中IMF_X的序号并不固定，个体之间存在差异. 为了消除个体差异，定义新参数：IMF_X在所有IMF中的几何位置P，P= ${X / {\sum {\rm{IMF}} }}$，X为分解得到的可评估血液流变特性的IMF的编号， $\sum {\rm{IMF}} $为分解得到的所有IMF的数量. 计算发现该参数仍然不是定值，且在2种氧气体积分数条件下，该参数的变化差异也不显著，如图7（b）所示. 图中， $\bar P $为P的平均值. 在不同受试者中，该参数的变化在2种氧气体积分数条件中未呈现明显规律性，大多数受试者表现为，在低氧环境中的 $\bar P$大于正常氧环境中的，如图7（c）所示. 图中，N为受试者序号.

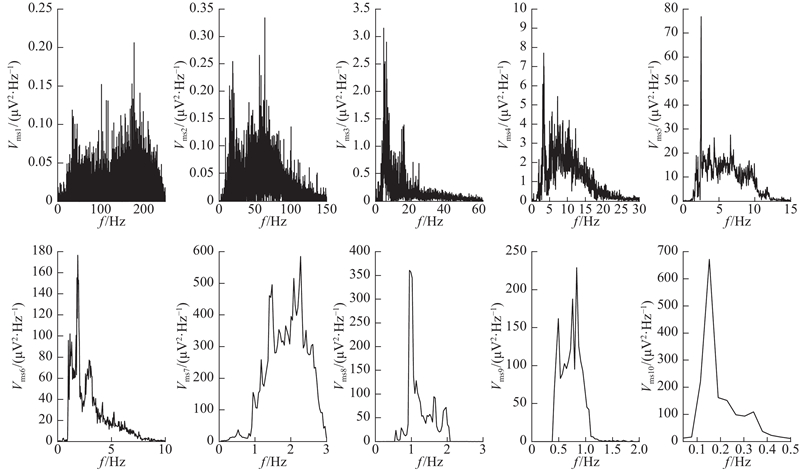
虽然PPG信号中实际表征血液流变信息的动力成分IMF_X的几何位置无明显规律性，但可以尝试从频域分析中提取其特征. 以图6中的IMF分解为例，图6中各IMF的Hilbert边际谱如图8所示，从左到右分别为IMF₁至IMF₁₀的边际谱图. 图中，f为瞬时频率，V_ms1~V_ms10分别为IMF₁~IMF₁₀边际谱振幅. 观察各IMF的边际谱瞬时频率及振幅，揭示各IMF隐藏的可能生理意义：1）IMF₁~IMF₄的边际谱振幅较小且高频成分占主导，可能是器械和其他干扰造成的高频噪声. 2）IMF₅之后的固有模式函数的瞬时频率主要集中在10 Hz以下，一般12 Hz以下符合正常生理范围^[26]，说明IMF₅之后的固有模式函数均属于人体自身生物信号. IMF₅、IMF₆的瞬时频率主要集中在1~3 Hz，但幅值较小，且从图6中观察不到两者形态上的周期振荡，其生理意义难以界定，可能是微弱的血管机械振荡或心脏调节. IMF₈~IMF₁₀的瞬时频率集中在1 Hz以下，理论上应属于类似呼吸的生理震动. 3）IMF₇是本研究寻找到的可评估血液流变特性的固有模式函数，重点关注此IMF的边际谱. 在该受试者的试例分解中，IMF₇的瞬时频率主要集中在1.5~2.5 Hz. 针对是否所有IMF_X的瞬时频率都集中在1.5~2.5 Hz这一猜想，对每位受试者在2种氧气体积分数情况下的IMF_X进行Hilbert边际谱分析.

为了证明所有IMF_X的瞬时频率均集中在1.5~2.5 Hz，对IMF_X的Hilbert边际谱做如图9所示的理论处理. 图中，V_ms为边际谱振幅. 分别计算IMF_X全段边际谱振幅曲线与频率轴形成的积分面积 ${S_1}$、瞬时频率落在1.5~2.5 Hz范围内的边际谱振幅曲线与频率轴形成的积分面积 ${S_2}$，并定义新参数面积比值 ${S_{\rm c}}$， ${S_{\rm c}} = {{{S_1}} / {{S_2}}}$，面积比值的大小表征瞬时频率集中在1.5~2.5 Hz的可能性. 比值越大，可能性越大；比值越小，可能性越小. 面积比值统计结果如图10所示，大部分受试者无论在正常氧体积分数条件还是低氧条件下，面积比值几乎都大于等于0.5，意味着IMF_X具有明显的频域特征，即人体PPG信号中可表征血液流变特性的固有模式函数IMF_X的瞬时频率范围为1.5~2.5 Hz.

由图9可以看出，2种氧气体积分数条件下边际谱的振幅也呈现较大区别，表现为低氧时的边际谱振幅小于正常氧情况下的. 统计所有受试者在2种氧气体积分数条件下的IMF_X边际谱的振幅差异，并做独立样本t检验，统计结果如表2所示. 结果表明，在全瞬时频率段，IMF_X边际谱振幅在不同氧气体积分数条件下不能够完全表现出显著性差异，有个别受试者差异不显著；1.5~2.5 Hz频率段的边际谱振幅幅值均表现出显著性差异，且规律为低氧条件下的振幅显著小于正常氧条件下的. 研究证明，PPG信号中某一动力分量IMF_X是实际表征血液流变变化的动力分量，可以根据其频域特征判断人体血液流变变化.

（1）使用EMD技术分解人体指端PPG信号，原始信号被分解为一系列具有不同振动模式的固有模态函数. 研究发现，其中的某个固有模态函数（自定义为IMF_X）是实际可以表征人体血液流变信息的动力分量. 确认依据是其具有类似动脉收缩和舒张波形且其具有明显可辨别的周期振荡性质.

（2）IMF_X的特点为，在不同个体中，其几何位置不同，不是固定的固有模式函数，但其频域特征统一表现为瞬时频率主要集中在1.5~2.5 Hz.

（3）IMF_X经Hilbert变换后，其1.5~2.5 Hz瞬时频率段的边际谱振幅对人体血液流变变化是敏感的. 表现为，正常氧气体积分数条件下与低氧条件下振幅具有显著性差异，趋势为低氧情况下振幅显著较低. 这种判别依据有可能成为人体在低氧环境生存极限的预警方法.

（4）本研究展示了使用指端PPG技术评估人体血液动力的可行性及利用HHT处理PPG信号的可行性，为这种便携廉价的设备技术的推广提供了理论支撑，且为特殊极端环境下人体血液流变变化无创检测提供了新思路. 接下来，希望结合成熟的医学手段严格证明本研究的研究结果.