吊杆是下承式和中承式拱桥的关键受力构件,在施工过程中它的张拉力不仅控制整个桥梁结构受力的合理性,而且影响主梁的线型、桥面的平顺和成桥后行车的安全舒适性,因此吊杆张拉力是评估拱桥结构状态的重要指标. 桥梁运营阶段的吊杆张拉力也是评估吊杆疲劳特性的重要指标. 因此,精确测定吊杆张拉力是拱桥施工和运营中的重要工作[1].
利用液压千斤顶的油压表直接测量吊杆张拉力是施工阶段张拉力测试的常用方法,但不适用于已张拉完成的吊杆[2]. 为了弥补油压表精度有限的缺点,可以通过安装专门的力传感器进行更加精确的测量,但只适合于施工阶段. 另外,力传感器的价格较高,导致额外增加成本[2]. 因此,简单快速和经济实惠的频率法在吊杆张拉力的验证性测试和长期监测中得到广泛应用. 该方法的缺点是吊杆的抗弯刚度和边界条件等因素均会影响其测试精度[3-11]. 此外还有三点弯曲法[2,12]和磁通量法[2,13-14]测试方法. 传统的频率法基于均匀截面柔性索的振动模型,但在实际工程中,柔性索无抗弯刚度的假设不一定合适,尤其当吊杆的长度较短或者两端边界条件较复杂时. 须根据实际情况调整计算索长来修正.
本研究所涉及的拱桥吊杆由于张拉施工的需要,设置了一定长度的连接螺杆和调节套筒. 在施工时将连接螺杆旋入套筒完成张拉,对于这种形式的吊杆,不能采用均匀截面的假定,而且由于螺杆和套筒的抗弯刚度较大,柔性索的假定也不适用. 本研究将其模拟为分段的受轴张拉力作用的梁. Naguleswaran[15-16]针对这类梁,给出其在轴力作用下自由振动的精确解,但须对每个分段依次求解. 实际上,传递矩阵法和动力刚度法也适用于截面特性分段变化的梁的振动分析[17-18]. 另外,很多研究工作没有考虑边界条件和索锚头部分的刚度的影响. 为此,本研究针对分段变截面的吊杆,发展基于状态空间法的动力分析方法,可精确模拟吊杆各部分不同的截面特性和材料参数,并详细考虑两端复杂的边界条件,得到吊杆频率与张拉力的理论关系,为该类吊杆张拉力的测试提供理论支撑.
1. 分析理论
1.1. 吊杆及其分析模型
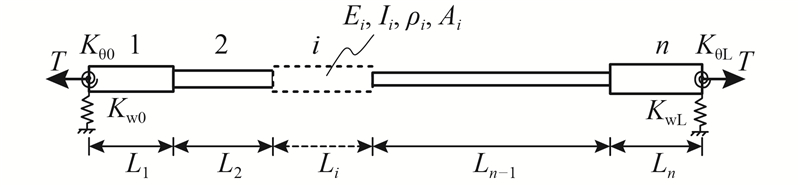
考虑如图1所示的拱桥吊杆,两端由于张拉施工和构造等原因,设置一定长度的叉耳、连接螺杆、调节套筒、连接头和锚头等构件. 显然,采用均匀截面柔性索假设的常规模型不适用,采用柔性索横向振动理论得到的频率与吊杆张拉力的解析关系也不成立,须发展新的分析方法.
图 1
本研究采用截面特性分段变化的受轴向张拉力的Euler-Bernoulli梁来模拟这种吊杆,如图2所示. 假设吊杆中不同截面特性和材料参数的梁段共有n段. 图中,T为吊杆张力,Ei为弹性模量,Ii为抗弯惯性矩,ρi为质量密度,Ai为截面积,Li为长度,下标i表示第i梁段,i=1, ···, n. 为了考虑工程中吊杆两端实际的边界条件,在两端分别设置具有横向刚度和扭转刚度的弹簧,Kw0、KwL为横向弹簧刚度,Kθ0、KθL为转动弹簧刚度. 通过调整弹簧刚度,可以模拟简支、固支以及一般弹性支撑的边界条件.
图 2
图 2 拱桥的分段变截面吊杆的梁模型
Fig.2 Beam model of hanger with stepped cross-section of arch bridge
1.2. 基于状态空间法的精确分析理论
对于如图2所示的分段变截面梁,先取第i段梁段为分析对象,根据轴向拉力T作用下Euler-Bernoulli梁自由振动理论,写出频率域内的控制方程以及内力与变形的关系:
式中:xi为第i段吊杆的坐标,i=1, 2,···, n;wi、θi、Mi、Qi分别为xi处的挠度、转角位移、弯矩、剪力的振型;ω为吊杆自由振动的圆频率. 在利用转角和挠度之间的关系
式中:
其中,L、h为2个具有长度量纲的常数,E、ρ、A、I分别为具有弹性模量、密度、面积和惯性矩量纲的常数. 式(3)是齐次的常微分方程,解为
在式(7)中取
式中:
对于每一段吊杆,都能得到如式(8)所示的传递关系,利用第i段吊杆与第i+1段吊杆在连接处的位移和内力连续条件,即
得到整个吊杆两端位移和内力之间的传递关系:
式中:
为了考虑吊杆两端一般的边界条件,可设吊杆两端的位移和内力之间关系如下:
式中:
其中,w0、θ0、Q0、M0分别为整根吊杆最左端的挠度、转角位移、剪力、弯矩;wL、θL、QL、ML分别为整根吊杆最右端的挠度、转角位移、剪力、弯矩;
将式(13)的4个条件与式(11)的4个方程合并在一起,写成如下的矩阵形式:
式中:
式(15)是齐次线性代数方程,有非零解的条件是其系数矩阵的行列式为零,即
式(17)是关于频率ω的超越方程,可以利用二分法求解. 在求得频率后,代回式(15),可以求得式(15)的非零解,即得到吊杆两端的内力和位移. 吊杆中间任意位置处的内力和位移可由式(7)求得.
对于两端简支的边界条件,可以取
将式(18)代入式(13)可以得到
此时,式(15)可以简化为
对于两端固结的边界条件,可以取
对于如图1所示的弹簧支承,可以取
其他的边界条件,可以在式(13)中取不同的参数
吊杆两端的边界条件可以写成矩阵形式:
式中:D1、Dn分别为端部条件矩阵,可以由吊杆两端的边界条件确定,即
将式(23)、(24)合并,并结合式(10)中位移和内力的连续条件,可以得到
式中:K为系统系数矩阵,V为系统变量列阵.
系统系数矩阵K可以分为两部分,即
式中:K1的维数为4n×4(n+1),K2的维数为4×4(n+1),表达式分别为
系统变量列阵V由各段截面处的状态向量排列构成,即
式(26)有非零解的条件是其系数矩阵的行列式为零,即
与式(17)类似,式(31)是JCM法的频率方程. 同样通过二分法可以求得频率ω,代回式(26)便可求得吊杆分段处的内力和位移,再利用式(7)可以求得任意位置处的内力和位移.
2. 方法验证
2.1. 工程概况及计算参数
为了验证所提方法,取某实际拱桥的吊杆为对象. 该吊杆是由上叉耳(开叉)、上叉耳(实心)、上锚头、索体、下锚头、连接头、调节套筒、下叉耳(实心)、下叉耳(开叉)九部分组成的变截面吊杆. 选取该拱桥的6根吊杆,分别记为1#、2#、3#、4#、5#、6#,各吊杆的物理参数除了索体其他各段均相同. 吊杆1#、2#、3#的索体长度分别为3.16、4.06、4.92 m,索体的弹性模量为1.95×1011 Pa,横截面积为1.37×10−3 m2,抗弯惯性矩为2.15×10−9 m4,密度为9.91×103 kg/m3. 吊杆4#、5#、6#的索体长度分别为4.75、4.12、3.28 m,索体的弹性模量为1.95×1011 Pa,横截面积为9.62×10−4 m2,抗弯惯性矩为1.50×10−9 m4,密度为1.01×104 kg/m3. 各吊杆的上叉耳(开叉)、上叉耳(实心)、上锚头、下锚头、连接头、调节套筒、下叉耳(实心)、下叉耳(开叉)的弹性模量为2.06×1011 Pa,密度为7.85×103 kg/m3,其他物理参数如表1所示. 吊杆两端的横向弹簧刚度Kw0=KwL=119.82×106 N/m,转动弹簧刚度Kθ0=KθL=2.6×106 N·m/rad.
表 1 吊杆的几何参数
Tab.1
| 参数 | Ai /(10−2 m2) | Ii /(10−6 m4) | Li /m |
| 上叉耳(开叉) | 2.09 | 84.30 | 0.300 |
| 上叉耳(实心) | 3.74 | 151.00 | 0.136 |
| 上锚头 | 3.55 | 3.89 | 0.260 |
| 下锚头 | 3.55 | 3.89 | 0.260 |
| 连接头 | 1.77 | 24.90 | 0.147 |
| 调节套筒 | 1.77 | 24.90 | 0.462 |
| 下叉耳(实心) | 3.74 | 151.00 | 0.136 |
| 下叉耳(开叉) | 2.09 | 84.30 | 0.300 |
2.2. 结果对比
将本研究方法计算所得的基频与现场张拉吊杆时测得的结果和有限元结果进行对比,以验证本研究方法. 有限元分析基于商用软件ABAQUS,采用B31单元,泊松比μ=0.3,吊杆的初张力用温度应力模拟,膨胀系数α=1.2×10−5 °C−1. 对于吊杆1#~6#的有限元模型,设定全局尺寸为2,软件将各吊杆分别划分成2 582、3 030、3 460、3 375、3 060、2 638个单元,这样的网格划分主要是为了保证模型计算收敛,同时不影响计算效率. 如图2所示,每根吊杆两端各设有2个弹簧,分别为横向支承弹簧和转动弹簧.
如表2所示为本研究方法计算所得基频与现场实测、有限元分析结果的比较. 表中,f0为本研究方法计算所得的基频,fT为现场张拉吊杆测得的基频,fF为有限元法计算所得的基频. 可以看出,本研究方法相对实测的误差绝对值的最大值为6.24%,最小值为0.21%,中位值为3.24%,平均值为3.22%;相对有限元的误差最大值为0.65%,最小值为0.01%,中位值为0.11%,平均值为0.18%. 如图3所示为6根吊杆用本研究方法与有限元法计算得到的振型. 图中,L为吊杆上任意一点与上叉耳(开叉)最外端之间的距离,D为吊杆上任意一点的振幅Di与最大振幅Dmax的比值. 可以看出,本研究方法所得结果与有限元结果较一致,说明本研究的分析理论具有足够的精度.
表 2 本研究方法计算所得基频与现场实测、有限元分析结果的比较
Tab.2
| 吊杆编号 | T/kN | f0 /Hz | fT /Hz | fF /Hz |
| 1)注:括号内数据为本研究结果相对实测结果的误差;2)注:括号内数据为本研究结果相对有限元结果的误差 | ||||
| 1# | 58.8 | 10.778 | 11.328(−4.86%)1) | 10.708(0.65%)2) |
| 2# | 147.0 | 12.636 | 13.477(−6.24%) | 12.616(0.16%) |
| 3# | 333.2 | 15.069 | 14.844(1.52%) | 15.042(0.18%) |
| 4# | 254.8 | 16.288 | 15.527(4.90%) | 16.287(0.01%) |
| 5# | 390.5 | 21.929 | 21.582(1.61%) | 21.921(0.04%) |
| 6# | 174.4 | 19.490 | 19.531(−0.21%) | 19.503(−0.07%) |
图 3
3. 有效计算长度的识别
为了实际工程中的应用方便,在已知吊杆振动频率的情况下,可以在上述计算方法的基础上尝试用显示表达式来计算吊杆张力. 由于吊杆索体部分的抗弯刚度较小,可以将其近似视为理想状态下的弦(EI=0),此时可以用经典的弦理论公式求解吊杆张力[20]:
式中:m为吊杆的线密度,l为吊杆的有效计算长度,fn为吊杆的第n阶自振频率. 对于索体较长的吊杆,式(32)计算结果较为准确,对于索体较短的吊杆,误差相对较大[21].
吊杆索体的两端设置有一定长度的叉耳、连接螺杆、调节套筒、连接头和锚头等构件(这些构件的刚度相对较大),因此直接将索体或者整根吊杆的实际长度作为有效计算长度都不合适,须对吊杆的有效计算长度进行识别.
假设每根吊杆的索体的弹性模量为1.95×1011 Pa,横截面积为1.37×10−3 m2,抗弯惯性矩为2.15×10−9 m4,密度为9.91×103 kg/m3. 给定吊杆张力T0=300 kN,吊杆的索体长度lc=0.5~10.0 m,每隔0.5 m取值. 根据本研究所提供的理论方法,可以计算出每根吊杆的理论基频f1,然后利用式(32)求得吊杆有效计算长度的第1次识别值l0,有效计算长度的识别结果如表3所示. 表中,T1为吊杆的计算张力.
表 3 吊杆有效计算长度的识别结果
Tab.3
| lc /m | f1 /Hz | l0 /m | l0 /lc | (0.984lc+0.339)/m | T1 /kN | [(T1−T0)/T0]/% |
| 0.5 | 37.118 | 2.002 | 4.005 | − | − | − |
| 1.0 | 33.294 | 2.232 | 2.232 | − | − | − |
| 1.5 | 30.847 | 2.409 | 1.606 | − | − | − |
| 2.0 | 28.236 | 2.632 | 1.316 | − | − | − |
| 2.5 | 25.194 | 2.950 | 1.180 | − | − | − |
| 3.0 | 22.174 | 3.352 | 1.117 | 3.291 | 289.211 | −3.60 |
| 3.5 | 19.561 | 3.800 | 1.086 | 3.783 | 297.364 | −0.88 |
| 4.0 | 17.407 | 4.270 | 1.067 | 4.275 | 300.717 | 0.24 |
| 4.5 | 15.643 | 4.751 | 1.056 | 4.767 | 301.982 | 0.66 |
| 5.0 | 14.187 | 5.239 | 1.048 | 5.259 | 302.297 | 0.77 |
| 5.5 | 12.970 | 5.730 | 1.042 | 5.751 | 302.169 | 0.72 |
| 6.0 | 11.942 | 6.224 | 1.037 | 6.243 | 301.834 | 0.61 |
| 6.5 | 11.061 | 6.719 | 1.034 | 6.735 | 301.409 | 0.47 |
| 7.0 | 10.301 | 7.216 | 1.031 | 7.227 | 300.952 | 0.32 |
| 7.5 | 9.637 | 7.713 | 1.028 | 7.719 | 300.494 | 0.16 |
| 8.0 | 9.053 | 8.210 | 1.026 | 8.211 | 300.051 | 0.02 |
| 8.5 | 8.535 | 8.708 | 1.025 | 8.703 | 299.629 | −0.12 |
| 9.0 | 8.073 | 9.207 | 1.023 | 9.195 | 299.231 | −0.26 |
| 9.5 | 7.658 | 9.705 | 1.022 | 9.687 | 298.859 | −0.38 |
| 10.0 | 7.284 | 10.204 | 1.020 | 10.179 | 298.511 | −0.50 |
图 4
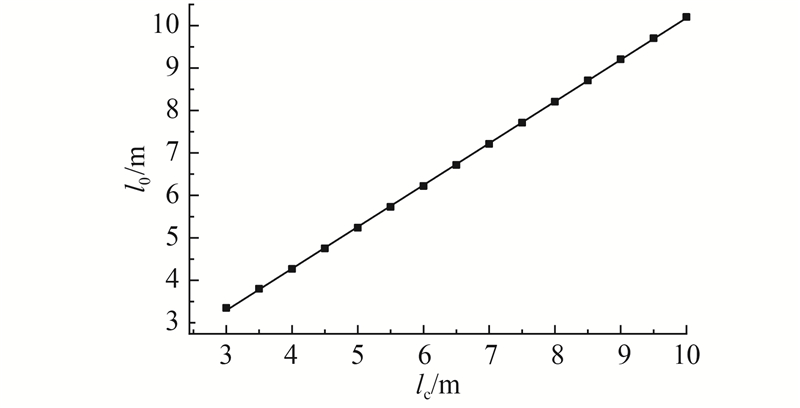
图 4 有效计算长度与索体长度的关系
Fig.4 Relationship between effective calculation length and length of cable segment
4. 结 论
(1)本研究针对变截面的吊杆,提出基于状态空间法的精确分析理论,给出吊杆频率与张力的关系,解决已有理论计算模型对吊杆截面的不均匀性、抗弯刚度、边界条件等参数考虑不全面的问题.
(2)将本研究提出的理论方法应用于某实际桥梁的吊杆张力分析,并将该理论方法分别与现场实测、有限元分析的结果进行对比,验证本研究方法的可靠性和精度.
(3)研究表明,当吊杆的索体长度大于某个值时,可用经典的弦理论公式求解吊杆张力,该公式中的有效计算长度l与索体长度lc存在较好的线性关系;在识别出与索体长度相关的吊杆有效计算长度后,在实际工程中运用弦理论公式来计算吊杆张力更为方便.
(4)本研究所得吊杆有效计算长度的通用性有待进一步研究.
参考文献
Technology developments in structural health monitoring of large-scale bridges
[J].DOI:10.1016/j.engstruct.2005.02.021 [本文引用: 1]
索结构中拉索张力测量的原理与方法
[J].
Principle and method of measuring cable tension in a cable structures
[J].
The linear theory of free vibrations of a suspended cable
[J].DOI:10.1098/rspa.1974.0189 [本文引用: 1]
A monitor for indirect measurement of cable vibration frequency and tension
[J].
A combined method for measuring cable forces: the cable-stayed Alamillo Bridge, Spain
[J].
Experimental determination of frequencies and tension for elastic cables
[J].DOI:10.1061/(ASCE)0733-9399(1998)124:10(1067)
Dynamic tests on large cable-stayed bridge
[J].DOI:10.1061/(ASCE)1084-0702(2001)6:1(54)
Empirical formulas to estimate cable tension by cable fundamental frequency
[J].
Estimation of cable tension force using the frequency-based system identification method
[J].
Practical formula for cable tension estimation by vibration method
[J].DOI:10.1061/(ASCE)BE.1943-5592.0000200
Tension determination of stay cable or external tendon with complicated constraints using multiple vibration measurements
[J].DOI:10.1016/j.measurement.2016.02.053 [本文引用: 1]
斜拉桥拉索索力测定的新方法
[J].
A new method determining cable tension on cable-stayed bridge
[J].
Monitoring based maintenance utilizing actual stress sensory technology
[J].DOI:10.1088/0964-1726/14/3/009 [本文引用: 1]
Sustainable structural health monitoring system
[J].
Vibration of an Euler–Bernoulli beam on elastic end supports and with up to three step changes in cross-section
[J].DOI:10.1016/S0020-7403(02)00190-X [本文引用: 1]
Vibration and stability of an Euler-Bernoulli beam with up to three-step changes in cross-section and in axial force
[J].DOI:10.1016/j.ijmecsci.2003.09.001 [本文引用: 1]
Free vibration analysis using the transfer-matrix method on a tapered beam
[J].
Free vibration of centrifugally stiffened uniform and tapered beams using the dynamic stiffness method
[J].DOI:10.1006/jsvi.1999.2855 [本文引用: 1]
Dynamic analysis of large space structures using transfer matrices and joint coupling matrices
[J].
斜拉桥的索力测试
[J].
Test of cable tension in cable-stayed bridges
[J].
考虑刚度及边界条件的索力精确求解
[J].DOI:10.3969/j.issn.1000-3835.2003.04.004 [本文引用: 1]
Precise solution of cable tensile force in consideration of cable stiffness and its boundary conditions
[J].DOI:10.3969/j.issn.1000-3835.2003.04.004 [本文引用: 1]