一般采用先定位后定量的两步策略来进行结构损伤识别[9-11]. 损伤定位的有效性影响损伤定量的计算效率与精度[11]. 因此,从某种意义上讲,损伤定位比损伤定量更为重要. 利用模态参数变化来定位结构损伤是当前的主流方法[12-14]. 其中,基于模态应变能的一类衍生指标被认为能够灵敏地反映结构损伤,在损伤定位研究中受到广泛关注[15-18]. 但是,大部分研究[15-18]仅针对规模较小的简单构件或结构的识别,不完全适用于规模庞大的复杂结构的识别. 在大跨空间结构领域,宋玉普等[19]针对网架结构的单损伤工况,先基于模态应变能筛选出疑似损伤构件,再采用最小二乘向量机完成损伤的定量估计;李永梅等[20]提出将模态应变能和小波变换相结合的方法对网壳结构进行损伤定位. 由于庞大的识别规模与测量噪声干扰之间的矛盾,有关大跨空间结构损伤定位的研究较少,且识别精度较低,发展抗噪能力更强的损伤定位指标是最基本的解决途径.
本研究提出基于跨模型模态应变能的损伤定位指标来判断网架结构(空间结构的典型代表)的损伤位置. 所提指标不仅改进了指标表达式,还引入了跨模型模态应变能的概念. 建立基于跨模型模态应变能的损伤定位指标理论公式,并对其抗噪性能进行定性分析;以具有较大识别规模的某网架结构为例进行数值分析,考察所提指标的有效性,分析影响抗噪性能提升的因素,并分析测量噪声、模态数量对损伤定位精度的影响.
1. 传统模态应变能指标
对于自由度数为n的结构,其模态方程为
式中:
定义在结构损伤前、后,单元j对应模态i的应变能表达式分别为
式中:
文献[19]采用模态应变能变化指标(modal strain energy change index,MSECI)来定位损伤. 单元j的MSECI指标如下:
式中:m为参与计算的模态数量;
其中,b为结构的单元数量.
可见,式(3)本质上是单元j归一化的模态应变能变化平均值.
文献[16]提出模态应变能基指标(modal strain energy based index,MSEBI)来定位损伤. 单元j的MSEBI指标表达式如下:
式中:
2. 跨模型模态应变能指标
定义单元j在结构损伤后对应模态i的跨模型模态应变能为
与式(2)中的
定义跨模型模态应变能增量表达式为
基于式(8)、(9),定义基于跨模型模态应变能的改进指标(modal-strain-energy modified index,MSEMI):
式中:
3. 跨模型模态应变能指标的误差分析
损伤结构的实测振型总是存在噪声污染,表达式为
式中:
将式(11)代入式(2),经整理后得到损伤结构单元j的传统模态应变能:
将式(11)代入式(8),得到损伤结构单元j的跨模型模态应变能为
将式(12)代入式(4),得到
式中:右端第1个括号内各项之和为未被噪声污染的传统模态应变能增量真实值;右端第2个括号内各项之和为误差.
将式(13)代入式(9),得到
式中:
比较式(14)、(15),并忽略式(14)中2个高阶项
4. 网架结构算例
4.1. 模型参数
以具有一定代表性的两向正放斜交四角锥网架为例进行数值分析,如图1所示. 结构尺寸为18 m×15 m×1.4 m(长×宽×高),上弦、下弦分别为7跨、6跨;结构为下弦支承,共有12个三向铰接支座;节点数量为113,构件数量为392;螺栓球直径均为100 mm. 构件只承受轴向力. 构件截面均采用直径为60 mm、壁厚为3.5 mm的无缝钢管,材料的弹性模量为206 GPa,泊松比为0.3,密度为7 850 kg/m3. 各节点编号如图1所示. 图中,加粗的构件为损伤模拟位置. 采用折减弹性模量的方法模拟构件损伤,模拟的损伤工况及损伤构件对应的节点如表1所示. 在模态分析时,同时考虑杆件和螺栓球自重对质量矩阵的贡献,每个螺栓球的质量为4.10 kg.
图 1
图 1 某18 m× 15 m平板网架示意图
Fig.1 Plan view of a space truss with a size of 18 m × 15 m
表 1 模拟的损伤工况及损伤构件对应节点
Tab.1
| 损伤工况 | 损伤构件 | 损伤程度 | 对应节点 |
| 1 | 81 | 0.30 | 41,43 |
| 2 | 101 | 0.30 | 88,103 |
| 141 | 0.40 | 21,36 | |
| 3 | 101 | 0.30 | 41,43 |
| 141 | 0.40 | 21,36 | |
| 300 | 0.30 | 68,82 |
4.2. 3种损伤定位指标的对比
为了模拟实测振型受噪声污染的影响,测量噪声的添加方式假定为
式中:
图 2
图 2 损伤工况1下的MSECI指标计算结果
Fig.2 Calculation results of MSECI index in damage scenario 1
图 3
图 3 损伤工况1下的MSEBI指标计算结果
Fig.3 Calculation results of MSEBI in damage scenario 1
图 4
图 4 损伤工况1下的MSEMI指标计算结果
Fig.4 Calculation results of MSEMI in damage scenario 1
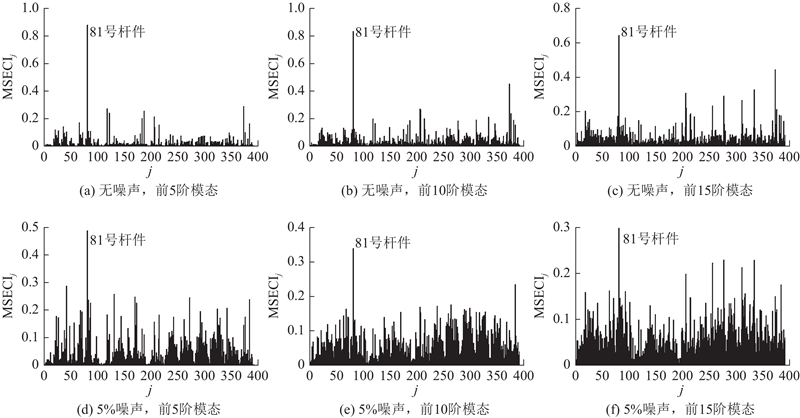
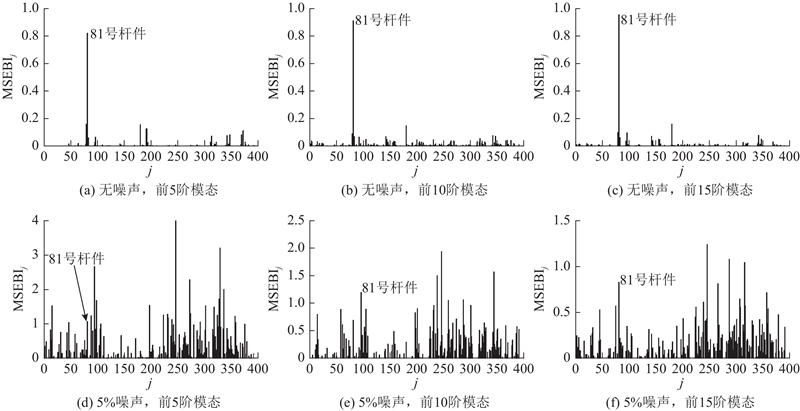
如图2(a)~(c)所示为不考虑噪声、变化模态数量情况下的MSECI指标计算结果. 在不考虑噪声的情况下,损伤构件(81号构件)对应的MSECI指标较大,损伤构件能够被明确指示出来;其他未损构件的干扰较多,且模态数量的增加反而增大了干扰. 文献[19]针对288杆网架结构进行计算分析,结果表明,即使不考虑噪声影响,MSECI指标也易受到未损构件的干扰. 如图2(d)~(f)所示为考虑5%噪声水平、变化模态数量情况下的MSECI指标计算结果. 在噪声影响下,虽然损伤构件均被明显指示出来,但相比无噪声的情况,未损构件的干扰明显增大;随着模态数量的增加,未损构件的干扰反而有所增大. 综上所述,在进行具有较大识别规模的网架结构损伤定位时,MSECI指标的抗噪能力较弱.
如图3(a)~(c)所示为不考虑噪声、变化模态数量情况下的MSEBI指标计算结果. 在不考虑噪声的情况下,损伤构件(81号构件)对应的MSEBI指标较大,其他未损构件的干扰较少,此时受模态数量变化的影响也较小. 如图3(d)~(f)所示为考虑5%噪声水平、变化模态数量情况下的MSEBI指标计算结果. 在噪声影响下,取5阶模态数量的MSEBI指标较小,损伤构件几乎完全湮没在其他未损构件的干扰中;取10阶模态数量的MSEBI指标有所突出,但仍不能明显指示81号构件的损伤状态;取15阶模态数量的MSEBI指标值更加突出,但部分未损构件的MSEBI指标也较大,使得对81号损伤构件的判断受到较大干扰. 可见,MSEBI指标的抗噪能力较弱,但增加参与计算的模态数量可以改善其抗噪性能. 这与文献[16]基于31杆平面桁架结构的研究结论(考虑3%噪声水平时MSEBI指标抗噪性强)有所冲突. 这是由于文献[16]采用的算例规模较小,且噪声水平相对较低. 综上所述,MSEBI指标的抗噪能力较弱,不适用于具有较大识别规模的网架结构损伤定位.
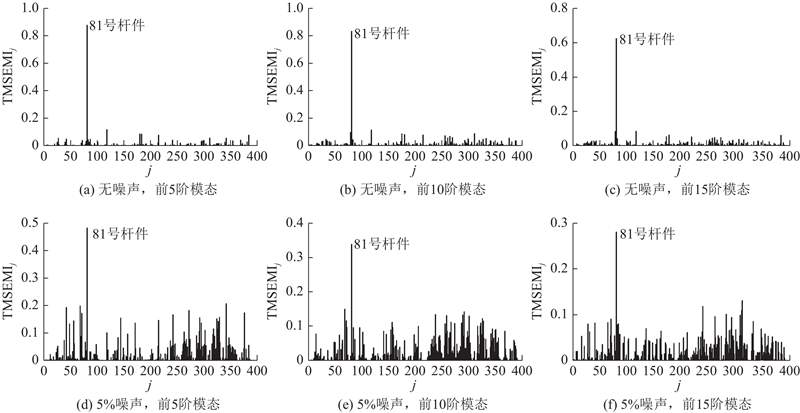
如图4(a)~(c)为不考虑噪声、变化模态数量情况下的MSEMI指标计算结果. 在不考虑噪声的情况下,损伤构件(81号构件)对应的MSEMI指标较大,其他未损构件的干扰较少,此时受模态数量变化的影响也较小. 如图4(d)~(f)所示为考虑5%噪声水平、变化模态数量情况下的MSEMI指标计算结果. 在噪声影响下,损伤构件对应的MSEMI指标均较大,其损伤状态能被明显指示出来;当取5阶模态数量时,MSEMI指标相对较差;当模态数量增加到10阶时,MSEMI指标明显好转;当继续增加模态数量到15阶时,MSEMI指标无明显改善. 可见,增加参与计算的模态数量可以适当改善MSEMI指标的抗干扰能力. 综上所述,与MSECI、MSEBI指标相比,MSEMI指标的损伤定位能力较强.
4.3. MSEMI指标的贡献因素分析
所提MSEMI指标既改进了表达形式,也引入了跨模型模态应变能. 因此,有必要分析这2个因素对所提指标抗噪性能的贡献.
图 5
图 5 损伤工况1下的TMSEMI指标计算结果
Fig.5 Calculation results of TMSEMI in damage scenario 1
由于噪声的随机性,须从统计意义上进一步分析跨模型模态应变能的引入对所提指标抗噪性能的改善作用.
4.3.1. ${C_{ij}}$ ${F_{ij}}$
定义Cij和Fij对应的相对波动参数(由噪声引起的误差与模态应变能增量真实值之比)分别为
式中:下标i、j分别为模态阶次和单元编号. 噪声是随机产生的,因此相对波动参数
采用蒙特卡洛方法获得
表 2 2种模态应变能增量所含噪声与真实值的相对波动幅度
Tab.2
| 模态i | 参数 | j=101 | j=141 | j=300 | ||||||||
| 最大值 | 最小值 | 波动幅 | 最大值 | 最小值 | 波动幅 | 最大值 | 最小值 | 波动幅 | ||||
| 1 | CNij | 3.09 | −1.55 | 4.64 | 5.71 | −2.17 | 7.88 | 127.70 | −2.27 | 129.98 | ||
| 1 | FNij | 2.21 | −1.69 | 3.91 | 3.45 | −3.23 | 6.69 | 26.08 | −3.97 | 30.05 | ||
| 2 | CNij | 2.34 | −1.56 | 3.90 | 1.41 | −1.16 | 2.56 | 122.15 | −1.85 | 124.00 | ||
| 2 | FNij | 1.76 | −1.71 | 3.46 | 1.09 | −1.19 | 2.28 | 22.34 | −3.11 | 25.45 | ||
| 3 | CNij | 3.06 | −1.79 | 4.85 | 16.69 | −6.51 | 23.20 | 7.13 | −2.13 | 9.26 | ||
| 3 | FNij | 2.15 | −2.10 | 4.25 | 11.16 | −10.97 | 22.13 | 4.06 | −3.11 | 7.17 | ||
| 4 | CNij | 1.02 | −0.79 | 1.81 | 1.06 | −1.00 | 2.06 | 1.35 | −0.94 | 2.29 | ||
| 4 | FNij | 0.78 | −0.76 | 1.55 | 0.84 | −1.01 | 1.85 | 1.01 | −0.93 | 1.94 | ||
| 5 | CNij | 1.44 | −1.25 | 2.69 | 0.61 | −0.36 | 0.97 | 9.16 | −4.44 | 13.60 | ||
| 5 | FNij | 1.28 | −1.27 | 2.55 | 0.33 | −0.24 | 0.57 | 6.50 | −6.21 | 12.71 | ||
| 6 | CNij | 20.09 | −2.84 | 22.93 | 10.41 | −2.59 | 13.01 | 395.86 | −1.03 | 396.88 | ||
| 6 | FNij | 9.44 | −5.12 | 14.56 | 5.73 | −4.61 | 10.35 | 22.14 | −1.18 | 23.32 | ||
| 7 | CNij | 0.95 | −0.64 | 1.58 | 2.02 | −1.40 | 3.42 | 20.00 | −1.03 | 21.03 | ||
| 7 | FNij | 0.71 | −0.59 | 1.30 | 1.47 | −1.51 | 2.99 | 4.29 | −1.22 | 5.51 | ||
| 8 | CNij | 0.56 | −0.51 | 1.07 | 2.86 | −2.11 | 4.96 | 2.11 | −1.15 | 3.27 | ||
| 8 | FNij | 0.44 | −0.47 | 0.91 | 2.11 | −2.55 | 4.67 | 1.49 | −1.19 | 2.68 | ||
| 9 | CNij | 18.40 | −1.19 | 19.59 | 9.93 | −2.07 | 12.01 | 0.79 | −0.69 | 1.48 | ||
| 9 | FNij | 5.09 | −1.67 | 6.76 | 5.01 | −3.54 | 8.55 | 0.62 | −0.65 | 1.28 | ||
| 10 | CNij | 0.52 | −0.42 | 0.94 | 0.56 | −0.42 | 0.99 | 3.63 | −1.21 | 4.84 | ||
| 10 | FNij | 0.34 | −0.33 | 0.67 | 0.33 | −0.31 | 0.64 | 1.72 | −1.56 | 3.29 | ||
4.3.2. 损伤构件受未损构件干扰的程度
基于前述5 000个噪声样本,取前10阶模态计算损伤工况1下每个样本的MSEMI指标和TMSEMI指标. 经统计,损伤构件(81号)对应的指标总是最大(即最能有效指示)的概率分别为99.82%、99.54%,表明这2种指标均具有较强的鲁棒性. 对于每个样本,分别将所有未损构件的指标平均值除以损伤构件相应的指标,从而得到2种指标各自对应的未损构件归一化平均值. 该归一化平均值的相对大小可以反映2种指标的抗噪性能. 值越小,相应指标的抗噪性能越好. 经统计,未损构件MSEMI指标归一化平均值大于TMSEMI指标归一化平均值的概率仅为3.08%,表明跨模型模态应变能的引入可以降低未损构件对损伤构件的干扰.
综上所述,定位指标表达式的改进对所提MSEMI指标的抗噪性能起主要作用,跨模型模态应变能的引入可进一步改善该指标应对随机噪声干扰的鲁棒性.
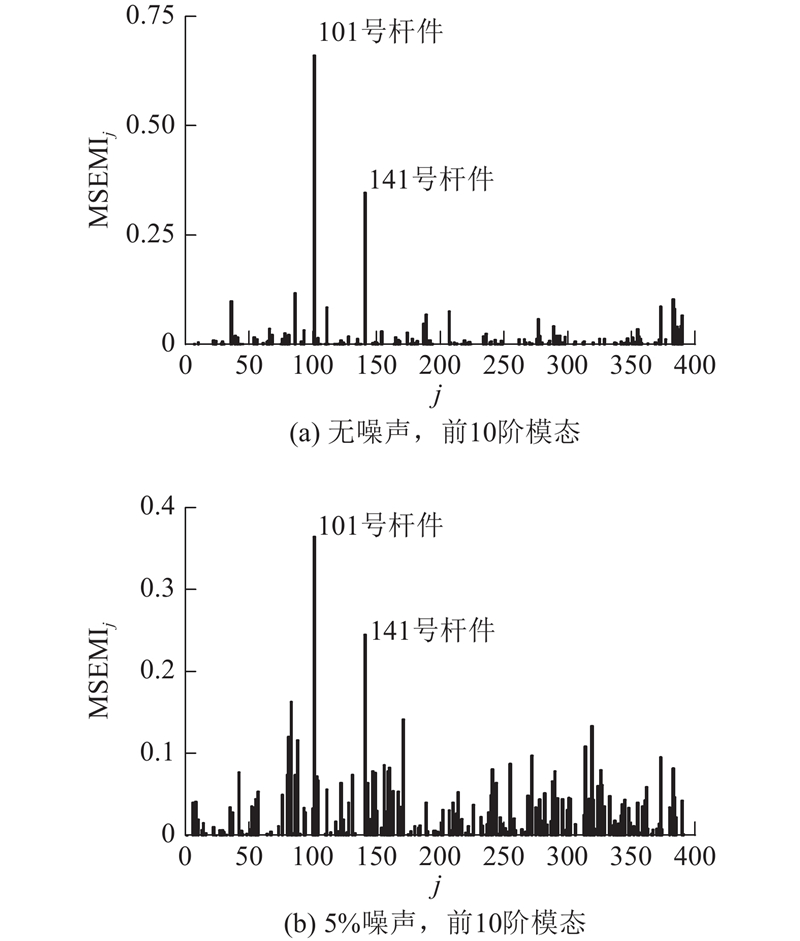
4.4. 基于MSEMI指标的多损伤工况分析
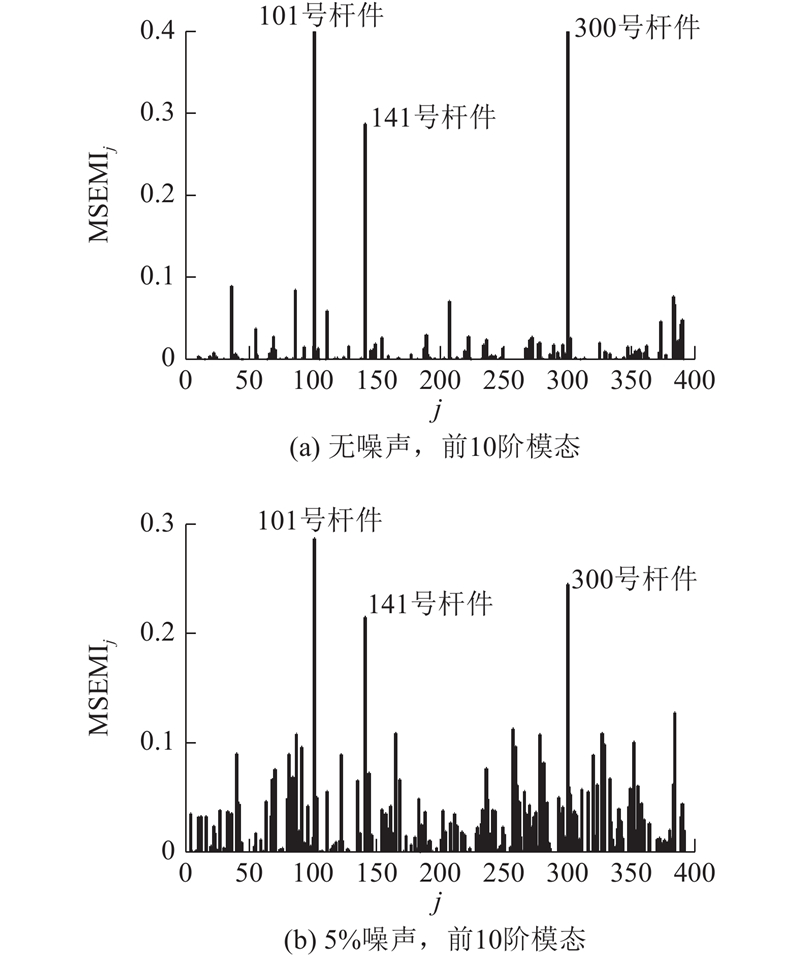
以如表1所示损伤工况2、3为例,考察MSEMI指标在多损伤工况下的表现. 选取前10阶模态参与MSEMI指标的计算. 在损伤工况2下,在无噪声、考虑5%噪声水平情况下的MSEMI指标计算结果分别如图6(a)、(b)所示. 由图6(a)可知,在无噪声时MSEMI指标能够清晰指示101号和141号损伤构件,所受干扰较小. 由图6(b)可知,在考虑5%噪声水平时,MSEMI指标所受干扰有所增大,但同样可以明确指示出2根损伤构件. 在损伤工况3下,在无噪声、考虑5%噪声情况下的MSEMI指标计算结果分别如图7(a)、(b)所示. 由图可知,即使考虑5%噪声水平,MSEMI指标依然能够清晰指示101号、141号以及300号损伤构件.
图 6
图 6 损伤工况2下的MSEMI指标计算结果
Fig.6 Calculation results of MSEMI in damage scenario 2
图 7
图 7 损伤工况3下的MSEMI指标计算结果
Fig.7 Calculation results of MSEMI in damage scenario 3
5. 结 论
(1)所提指标MSEMI既改进了指标表达式,又引入了跨模型模态应变能. 指标表达式的改进对所提指标的抗噪性能提升起主要作用,而跨模型模态应变能的引入可以进一步改善所提指标的鲁棒性.
(2)定性分析和蒙特卡洛分析均表明,损伤单元跨模型模态应变能增量比传统模态应变能增量受噪声影响的程度更小,基于跨模型模态应变能建立的损伤定位指标较优.
(3)算例表明,所提MSEMI指标比传统模态应变能指标MSECI、MSEBI的抗噪能力更强,更适用于具有较大识别规模的网架结构损伤定位;较多的模态数量(对于本算例,建议取10阶)有利于增强MSEMI指标的抗噪能力.
(4)与传统模态应变能类似,基于跨模型模态应变能也可以衍生出诸多损伤定位指标,它们的性能有待进一步研究.
参考文献
Restoring method for missing data of spatial structural stressmonitoring based on correlation
[J].DOI:10.1016/j.ymssp.2017.01.018 [本文引用: 1]
新型六杆四面体柱面网壳的构形、静力和稳定性分析
[J].
Configuration, static and stability analysis on new-type six-bar tetrahedral cylindrical lattice shells
[J].
天津理工大学体育馆新型复合式索穹顶结构风振效应分析
[J].
Time-history analysis of wind vibration response for the cable dome of gymnasium at Tianjin University of Technology
[J].
巴黎戴高乐机场候机楼倒塌事故原因初析
[J].
Paris airport terminal collapse: lessons for the future
[J].
基于AR模型与BP神经网络的网壳结构损伤识别方法研究
[J].
Study on the damage detection method for latticed shell structures
[J].
Damage detection in grid structures using limited modal test data
[J].
基于附加虚拟质量的结构损伤识别方法
[J].DOI:10.7511/jslx201306004 [本文引用: 1]
Structural damage identification using additional virtual masses
[J].DOI:10.7511/jslx201306004 [本文引用: 1]
Damage detection of truss structures using two-stage optimization based on micro genetic algorithm
[J].DOI:10.1007/s12206-014-0830-y [本文引用: 1]
基于剩余模态力和模态应变能理论的网架结构损伤识别
[J].DOI:10.3969/j.issn.1000-4750.2007.05.016
Damage detection of space truss using residual modal force and modal strain energy
[J].DOI:10.3969/j.issn.1000-4750.2007.05.016
A fast and robust method for damage detection of truss structures
[J].DOI:10.1016/j.apm.2018.11.025 [本文引用: 2]
Modal curvature-based damage localization in weakly damaged continuous beams
[J].DOI:10.1016/j.ymssp.2018.11.012 [本文引用: 1]
基于振型加权模态柔度的梁桥损伤识别方法
[J].
Damage identification method for beam bridge based on mode shape weighted modal flexibility
[J].
基于振型相关度的网壳结构状态特征向量试验研究
[J].
Experimental study on structural condition characteristic vector of latticed domes based on modal correlation
[J].
Structural damage localization from modal strain energy change
[J].DOI:10.1006/jsvi.1998.1878 [本文引用: 2]
A two stage method for structural damage detection using a modal strain energy based index and particleswarm optimization
[J].
基于应变能等效指标的结构损伤识别技术研究
[J].DOI:10.3969/j.issn.0254-7805.2013.03.009
Structural damage identification method based on strain energy equivalence parameter
[J].DOI:10.3969/j.issn.0254-7805.2013.03.009
Detecting damage in steel beams using modal strain energy based damage index and artificial neural network
[J].DOI:10.1016/j.engfailanal.2017.04.035 [本文引用: 2]
测量模态不完整情况下空间网架结构的损伤识别
[J].
Damage identification of space truss with incomplete measured data
[J].