上述研究均只适用于线弹性结构. 当结构间距较小时,可近似认为相邻结构在发生碰撞前处于线弹性阶段;当相邻结构的间距大于单体结构弹性层间位移角限值对应的层间位移时,在发生碰撞前,结构构件会发生塑性变形. 因此,须考虑相邻结构非线性行为对地震碰撞的影响. 此外,为了促进基于性能的抗震设计理论的发展,亟需提出新的、先进的、准确的、高效的、对系统特性无要求的基于可靠度的方法来评估相邻结构的地震碰撞风险.
1. 基于子集模拟的相邻结构地震碰撞易损性与风险评估方法
1.1. 地震碰撞易损性与风险定义
地震碰撞发生的条件为在地震作用下相邻结构的相对位移时程Urel(θ,t)峰值(仅限相向运动)大于等于结构间距
式中:IM为地震强度指标,im为对应的具体量值,tmax为地震动持时.
定义地震危险性曲线为地震烈度的年均超越概率[13]:
式中:k0、k1为根据对数坐标下的场地危险性曲线上的2个已知点进行直线拟合得到的参数.
因此,相邻结构年均地震碰撞概率为
假定一次碰撞事件的出现可以通过泊松过程描述[13],则相邻结构在设计使用年限tL内的地震碰撞风险可通过年均碰撞概率表示为
值得注意的是本研究仅对相邻结构发生地震碰撞的易损性及风险进行分析,不考虑地震碰撞对结构易损性及风险的影响.
1.2. 子集模拟法
为了开展相邻结构的地震碰撞易损性与风险分析,并考虑结构非线性的影响,引入子集模拟法[18]对式(1)的失效概率进行计算. 该方法是针对小失效概率问题的高效可靠度方法,不依赖任何具体问题信息,而是将不确定性参数与响应间的输入输出关系作为黑匣子处理.
1)基本思想. 令
其中,
因此,通过引入合理的中间失效事件,可将概率空间划分为一系列具有序列包含关系的子集,从而将小失效概率转化为一系列较大的条件失效概率乘积的形式,极大提高计算效率.
2)计算步骤. a)利用蒙特卡罗模拟法生成N个样本
式中:
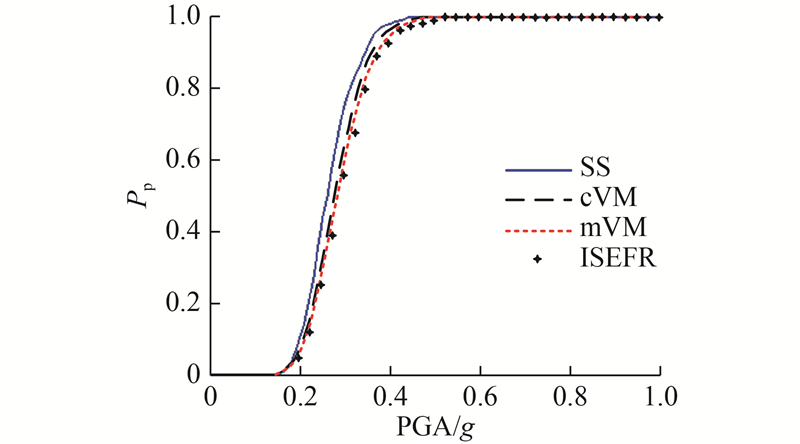
2. 采用不同方法的线性相邻结构地震碰撞易损性计算结果对比
假定相邻单自由度线性结构周期分别为TA=1 s,TB=0.5 s,阻尼比
2.1. 随机地震作用
假定相邻结构所受随机地震作用为均匀调制非平稳随机过程,由时间调制函数与平稳随机过程的乘积确定.
时间调制函数表达式为
式中:
平稳随机过程的功率谱密度函数采用Clough-Penzien模型:
式中:ω为频率变量;
利用谱分解方法[19]生成平稳随机过程:
式中:
2.2. 地震碰撞易损性对比
将峰值地面加速度(peak ground acceleration,PGA)作为地震强度指标IM,通过对各条地震波的PGA进行调幅,计算不同PGA下的相邻结构峰值相对位移,其中地震波持时取30 s,时间间隔取0.02 s.
图 1
3. 非线性相邻结构地震碰撞易损性与风险评估
3.1. 运动方程及确定性时程分析
图 2
式中:
其中,
假定该相邻结构各参数取值如下[20]:
由上述参数可以得到左侧结构自振频率为0.83 Hz,右侧结构自振频率为3.33 Hz,约为左侧结构自振频率的4倍.
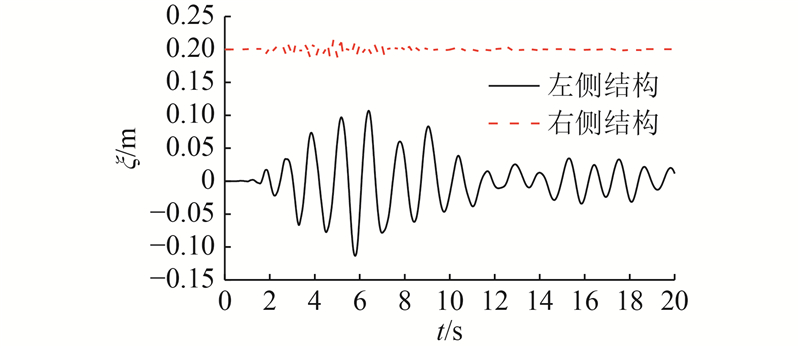
为了直观掌握该非线性相邻结构的响应特征,假定结构间距为0.2 m,对其输入El-Centro地震波,峰值地面加速度为3.48 m/s2,持时为20 s,时间间隔为0.002 s. 利用逐步积分的Newmark-β法计算其在地震作用下的位移响应,在此种情况下不发生结构碰撞,其中相邻结构3层的位移时程如图3所示.
图 3
图 3 非线性相邻结构不发生碰撞时第3层的位移响应
Fig.3 Displacement response of third story in nonlinear adjacent structures without pounding
根据计算结果可知,左侧结构第1、2、3层的峰值位移分别为0.066、0.100、0.121 m,右侧结构第1、2、3层的峰值位移分别为0.010、0.015、0.018 m,可以发现右侧较刚结构的位移远小于左侧较柔结构;各层峰值相对位移分别为0.060、0.098、0.122 m.
3.2. 地震碰撞易损性分析
利用子集模拟法计算该相邻结构发生地震碰撞的易损性,其中N=200,p0=0.1. 随机地震波的生成方式同2.1节,持时为20 s,时间间隔为0.002 s,则不确定性参数维数为10 000. 通过该相邻结构在随机地震作用下的时程分析发现,若结构在第1层发生碰撞,则在第2、3层也必会发生碰撞,且碰撞在同一时刻出现.
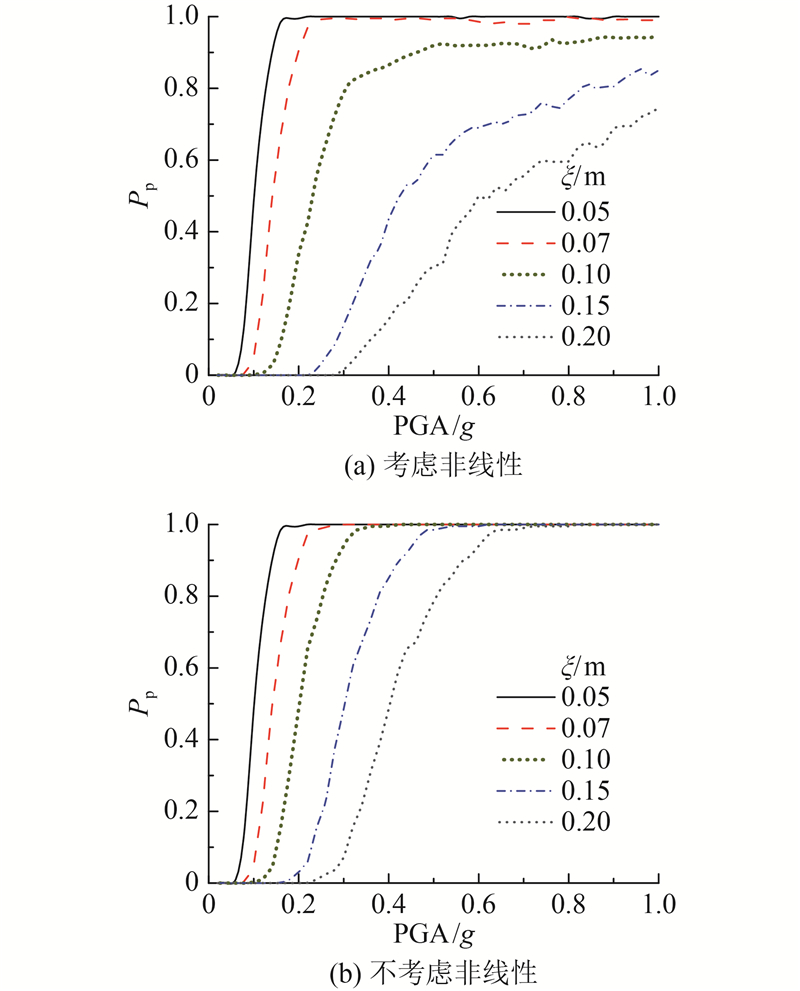
图 4
图 4 不同间距下相邻结构地震碰撞易损性曲线
Fig.4 Fragility curves of seismic pounding for adjacent structures at different separation distances
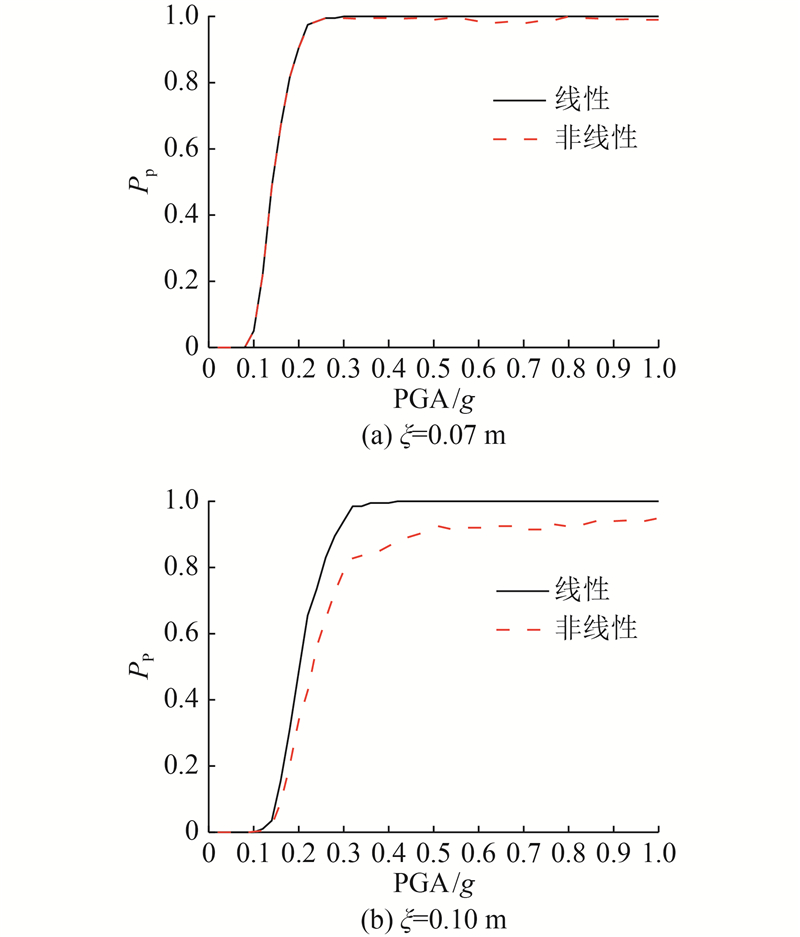
图 5
图 5 考虑与不考虑非线性的相邻结构地震碰撞易损性曲线对比
Fig.5 Comparison of seismic pounding fragility curves between adjacent structures with and without considering nonlinear behavior
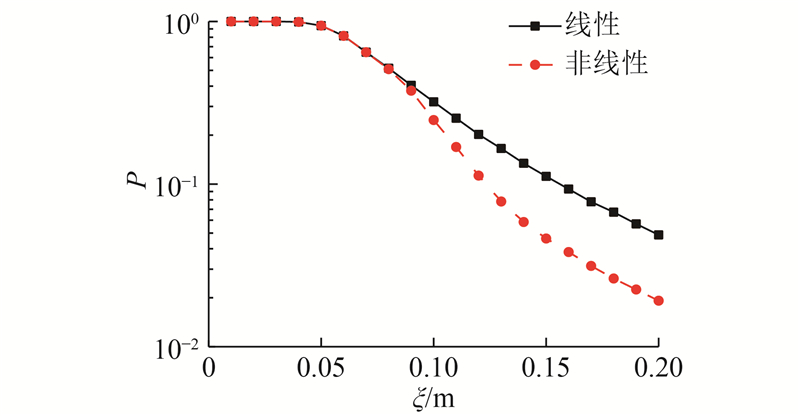
对图4、5进行分析可知,1)无论考虑非线性与否,结构间距越小,在相同的峰值地面加速度下失效概率越大. 例如,当峰值地面加速度为0.3g,结构间距分别为0.05、0.07、0.10、0.15、0.20 m时,考虑非线性时发生地震碰撞的失效概率分别为1.000、0.995、0.790、0.140、0.015. 2)考虑非线性的相邻结构地震碰撞易损性曲线与不考虑非线性的相邻结构地震碰撞易损性曲线不同,虽然总体呈增大趋势,但局部有微小波动. 原因如下:在邻近峰值地面加速度下,由于结构的非线性效应,相邻结构的相对位移不一定增大,在易损性曲线上会产生小幅波动;当不考虑结构非线性时,随着峰值地面加速度的增大,相邻结构的峰值相对位移一定增大;当考虑非线性时,当结构间距为0.10、0.15、0.20 m时,即使峰值地面加速度增大至1.0g,失效概率也不会达到1.000. 3)结构间距越大,考虑非线性与否的失效概率差别越大,且线性相邻结构的失效概率大于非线性相邻结构,计算结果偏于保守. 原因如下:结构间距越大,在结构碰撞前进入非线性的可能性及程度就越大,在结构屈服后由于自振周期延长,峰值相对位移减小.
当结构间距为0.05、0.07 m时,考虑非线性与否的失效概率近似相等;当峰值地面加速度分别为0.22g和0.24g时,失效概率为1.000,表明在此间距下,相邻结构发生碰撞时对应的峰值地面加速度较小,结构处于线性阶段.
此外,为了验证利用子集模拟法计算非线性相邻结构地震碰撞易损性的正确性,将蒙特卡罗法的计算结果(样本数取2 000)作为精确解,对部分工况进行对比,如表1所示. 可以看出,两者较吻合,子集模拟法具有较高的计算精度.
表 1 结构间距为0.10 m时非线性相邻结构的失效概率对比
Tab.1
| 算法 | PGA | ||||
| 0.12g | 0.14g | 0.20g | 0.40g | 0.60g | |
| 子集模拟法 | 0.005 0 | 0.020 0 | 0.340 0 | 0.865 0 | 0.920 0 |
| 蒙特卡罗法 | 0.004 8 | 0.021 0 | 0.340 0 | 0.865 0 | 0.920 0 |
3.3. 地震碰撞年均及设计使用年限内失效概率计算
根据对应PGA=0.3g的地震重现周期为475 a,即50 a超越概率为10%,将场地危险性曲线[9]表示为
图 6
图 7
4. 结构间连接对相邻结构地震碰撞易损性的影响分析
4.1. 运动方程及确定性时程分析
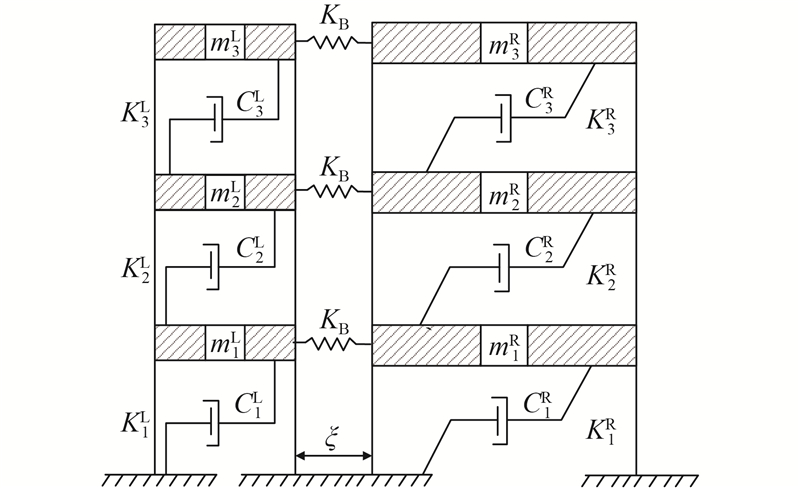
当结构间距不足时,结构间连接是常用的减撞手段. 假定相邻结构在各层处相互连接,连接弹簧单元在结构间距范围内可自由变形,连接刚度为KB,相邻结构模型如图8所示.
图 8
图 8 弹簧单元连接的相邻结构模型
Fig.8 Model of adjacent structures linked by spring elements
在地震作用下运动方程[20]为
式中:
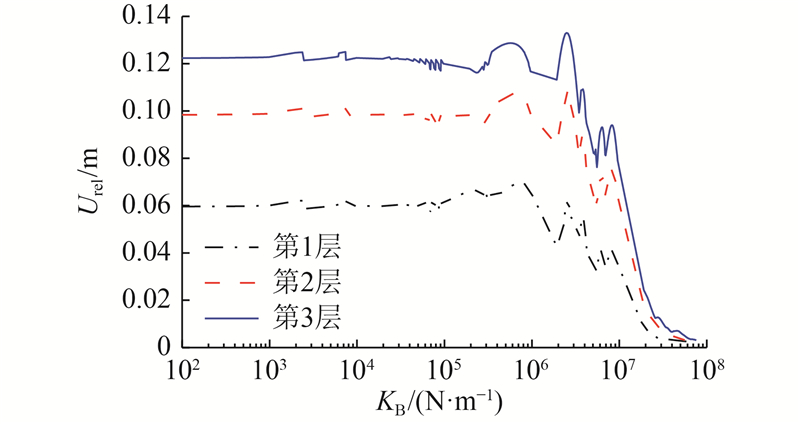
为了直观掌握考虑连接后的非线性相邻结构响应特征,对其输入El-Centro地震波,持时为20 s,时间间隔为0.002 s,不同连接刚度下相邻结构峰值相对位移的变化规律如图9所示. 可以看出,增大连接刚度不一定会减少结构地震碰撞. 当连接刚度较小时,峰值相对位移基本不变;当连接刚度为105~107 N/m时,由于结构间连接改变了相邻结构的运动方式,峰值相对位移甚至出现增大的现象;随着连接刚度的继续增大,峰值相对位移单调减小. 在其他地震波作用下,也会出现类似的现象,但是峰值相对位移增大对应的连接刚度范围不同.
图 9
图 9 不同连接刚度下相邻结构的峰值相对位移
Fig.9 Peak relative displacements of adjacent structures with different linking stiffness values
4.2. 考虑结构间连接的地震碰撞易损性分析
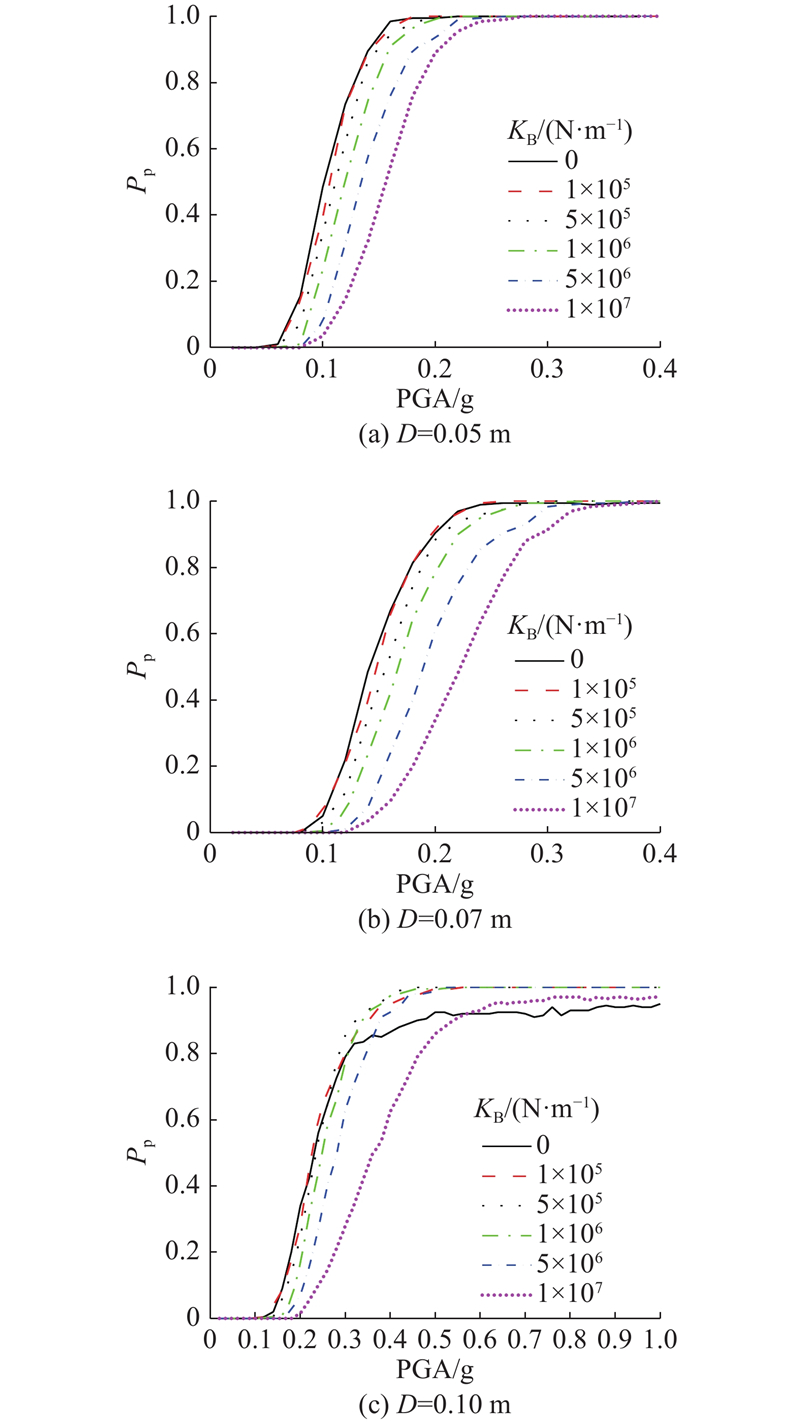
生成随机地震波,并利用子集模拟法对不同连接刚度的减撞效果进行评估,其中涉及的参数取值同3.2节. 当结构间距为0.05、0.07、0.10 m,连接刚度分别为0、1×105、5×105、1×106、5×106、1×107 N/m时的相邻结构地震碰撞易损性曲线如图10所示. 可以看出,1)当结构间距为0.05、0.07 m时,在较小的峰值地面加速度下就会发生地震碰撞,即结构在碰撞前处于线性阶段,此时随着连接刚度的增大,碰撞概率减小;以连接刚度为106 N/m(与左侧较柔结构层间刚度为同一量级)、峰值地面加速度为0.16g为例,2种间距下的碰撞概率分别为0.91、0.42,比无连接时的碰撞概率0.985、0.670,分别降低7.5%、25.0%;当峰值地面加速度分别为0.28g、0.40g时,在各连接刚度下相邻结构的地震碰撞概率均为1.000. 2)当结构间距为0.10 m时,发生地震碰撞对应的峰值地面加速度较大,即结构在碰撞前进入非线性阶段. 当连接刚度为1×105~1×107 N/m时,当峰值地面加速度大于一定值时(该值随连接刚度增大而增大),结构间连接反而使得地震碰撞概率比无连接时增大. 说明在此间距下,仅当连接刚度足够大时,结构间连接才会使得失效概率一定减小.
图 10
图 10 不同连接刚度的相邻结构地震碰撞易损性
Fig.10 Fragility curves of seismic pounding for adjacent structures with different linking stiffness values
5. 结 语
提出基于子集模拟的相邻结构地震碰撞易损性与风险评估方法,并应用于动力特性差异显著的非线性相邻结构. 分析考虑非线性与否对相邻结构地震碰撞易损性的影响,结果表明,非线性相邻结构的地震碰撞易损性曲线总体呈增大趋势,但局部存在微小波动;当结构间距大于一定值后,即使峰值地面加速度增大,失效概率也不会达到1.000;结构间距越大,考虑非线性与否的地震碰撞概率差别越大,且不考虑非线性的计算结果偏于保守. 因此,考虑结构非线性影响制定相邻结构临界间距,更有利于土地的有效利用.
对采用结构间连接减轻间距不足的相邻结构地震碰撞的效果进行概率评估,结果表明,对于在发生碰撞前结构处于线性阶段的结构间距,采用不同的连接刚度均会降低碰撞概率;对于在发生碰撞前结构进入非线性阶段的结构间距,只有当连接刚度足够大时,碰撞概率才会一定降低. 因此,利用结构间连接作为减撞措施时,须保证一定的连接刚度.
参考文献
Building pounding damage observed in the 2011 Christchurch earthquake
[J].DOI:10.1002/eqe.1164 [本文引用: 1]
Performance of medium-to-high rise reinforced concrete frame buildings with masonry infill in the 2015 Gorkha, Nepal, Earthquake
[J].
芦山地震中相邻建筑碰撞破坏调查与分析
[J].DOI:10.11918/j.issn.0367-6234.2015.12.018
Investigation and analysis on adjacent buildings pounding damage in Lushan Earthquake
[J].DOI:10.11918/j.issn.0367-6234.2015.12.018
建筑物的变形缝在汶川地震中的反应及对策思考
[J].
Reflections on counter measures and responses of joints of structures in Wenchuan Earthquake
[J].
A general spectral difference method for calculating the minimum safety distance to avoid the pounding of adjacent structures during earthquakes
[J].DOI:10.1016/j.engstruct.2017.07.068 [本文引用: 1]
Numerical simulation of potential seismic pounding among adjacent buildings in series
[J].
Assessment of the separation necessary to prevent seismic pounding between linear structural systems
[J].DOI:10.1016/j.probengmech.2008.06.002 [本文引用: 1]
A probabilistic performance-based approach for mitigating the seismic pounding risk between adjacent buildings
[J].DOI:10.1002/eqe.2267 [本文引用: 4]
Separation distance to avoid seismic pounding of adjacent buildings
[J].DOI:10.1002/(SICI)1096-9845(199703)26:3<395::AID-EQE655>3.0.CO;2-F [本文引用: 1]
地震作用下梁体碰撞间隙宽度的概率分析方法
[J].DOI:10.6052/j.issn.1000-4750.2017.03.0263 [本文引用: 1]
Probability analysis of pounding separation distance of bridges subjected to earthquake excitations
[J].DOI:10.6052/j.issn.1000-4750.2017.03.0263 [本文引用: 1]
随机地震激励下高墩桥梁碰撞可靠度分析
[J].DOI:10.3969/j.issn.0258-2724.2018.01.011 [本文引用: 1]
Dynamic reliability analysis on pounding of high-pier bridges subjected to stochastics seismic excitations
[J].DOI:10.3969/j.issn.0258-2724.2018.01.011 [本文引用: 1]
A probabilistic performance-based risk assessment approach for seismic pounding with efficient application to linear systems
[J].DOI:10.1016/j.strusafe.2012.01.002 [本文引用: 5]
Probabilistic seismic demand model for pounding risk assessment
[J].DOI:10.1002/eqe.2725 [本文引用: 1]
Seismic fragility analysis of adjacent inelastic structures connected with viscous fluid dampers
[J].DOI:10.1177/1369433216646000 [本文引用: 1]
Relaxation method for pounding action between adjacent buildings at expansion joint
[J].DOI:10.1002/eqe.2402 [本文引用: 1]
Seismic pounding between adjacent buildings: identification of parameters, soil interaction issues and mitigation measures
[J].DOI:10.1016/j.soildyn.2019.02.024 [本文引用: 1]
Estimation of small failure probabilities in high dimensions by subset simulation
[J].DOI:10.1016/S0266-8920(01)00019-4 [本文引用: 3]
Simulation of stochastic processes by spectral representation
[J].DOI:10.1115/1.3119501 [本文引用: 1]
Linking of adjacent three-storey buildings for mitigation of structural pounding during earthquakes
[J].DOI:10.1007/s10518-016-9946-z [本文引用: 3]