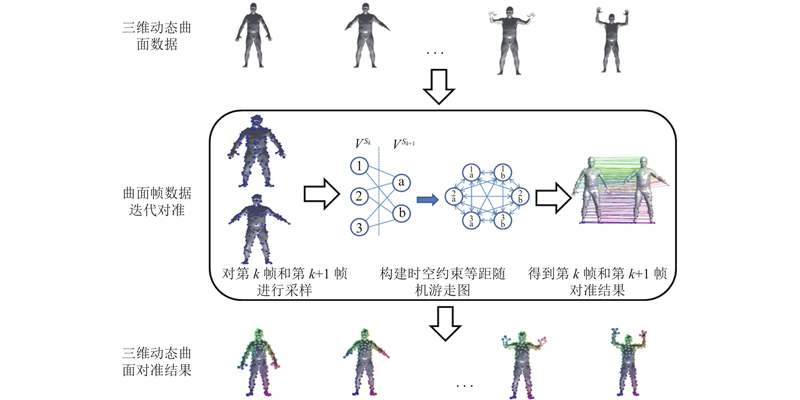
三维动态曲面对准（three-dimensional dynamic surface alignment）是计算机图形学的一个基础性问题，也是实现高质量三维动态重建的前提和基础. 如何建立可靠的三维动态曲面对准关系，也是当前研究急需解决的一个问题.

和三维动态曲面对准问题非常相关的一个问题是三维数据非刚性对应（three-dimensional non-rigid correspondence）问题. 目前在这方面有很多研究，这些非刚性对应算法针对流形数据得到很好的对应结果. 对于具有高噪声和残缺的三维动态曲面，由于拓扑变化、噪声和残缺数据的影响，导致对应结果包含大量的错误匹配关系. 采用跟踪算法实现三维动态曲面对准会因为动作变化大，导致跟踪丢失^[1]. 对于三维动态曲面对准，Sahillioğlu等^[2]考虑采用测地距离计算对应关系来优化结果. 该方法只是采用测地距离计算局部描述符，并进行约束求解. 针对三维非刚性数据所提出的测地距离极大似然优化算法，只是通过局部调整来优化对应结果.

本文在已有等距对应优化计算的基础上，针对三维动态曲面，提出时空等距随机游走图. 该算法的主要思想是在相邻两帧数据的乘积空间中以候选匹配对作为图节点，以测地距离定义边权重，形成可以通过随机游走进行求解的图模型，解决等距对应问题. 通过马尔可夫链理论，计算三维动态曲面对准. 通过实验分析表明，提出的随机游走模型能够稳定、可靠地计算得到匹配关系，而且优于已有算法.

本文通过等距性来解决三维动态曲面的对应问题. 主要的相关工作包括2部分：1）针对三维非刚性对应所建立起来的等距模型；2）针对三维动态曲面，采用测地距离提高算法准确性.

三维数据在发生非刚性变换时，具有测地距离稳定性. 研究人员考虑采用测地距离定义等距对应算法. Bronstein等^[3]通过多维缩放方法，利用测地距离将一个模型嵌入另一个模型来计算对应关系. Sahillioğlu等^[2]在原欧式空间中使用等距匹配，他们提出分级投票联合方法（rank-and-vote-and-combine, RAVAC）来实现局部对应. 潘翔等^[4]针对已有等距映射算法缺少局部特征约束所导致的错误对齐问题, 提出等距二分图三维模型对齐算法来提高算法精度. 对于局部特征约束，可以采用DAISY等其他描述符^[5]. 在测地距离基础上，Ovsjanikov等^[6]提出热核信号，该描述符在非刚性变换下具有很好的稳定性和保距性. 循环一致性对应是以局部形状符定义候选匹配对，采用二次规划和测地空间完成约束求解，得到对应结果^[7-8]. 核匹配采用测地距离定义矩阵，通过凸规划和投影梯度下降优化完成求解. 这种方法对于流形和拓扑维持的三维数据能够得到很好的对应结果^[9]. 拉普拉斯-贝尔特拉米特征函数是通过测地距离得到的谱信号^[10]. 多维缩放是考虑把点映射到另外一个空间，并保留映射空间的距离不变性，该方法被称为广义多维尺度变换(MDS)^[11].

三维动态曲面对准，可以采用测地距离来提高对应结果. 对三维动态曲面采用测地距离定义跟踪骨架，通过正则化方法完成求解是最典型的方法. 战江涛等^[12]采用测地距离定义三维人脸几何模型，提高人脸特征点跟踪系统的鲁棒性和精确性. 对于跟踪方法，可以对正则化模型进行改进，在关节位置加入隐含约束变形，避免跟踪误差的传播，从而提高跟踪鲁棒性，但是该方法存在跟踪丢失问题^[1]. 测地映射方法是由表面之间的距离函数（即全局测地距离）定义测地微分同胚，建立广义重心坐标下的测地坐标系，用以可靠地定位对准关系^[13]. 匹配树是通过测地距离计算三维动态曲面非刚性形变的最小误差，避免跟踪丢失问题并实现全局对齐^[14]. 特征跟踪是通过测地距离定义局部坐标系，结合近似不变的特征向量和几何运动流向量实现大形变的特征跟踪，用以解决拓扑不一致性的特征跟踪问题^[15].

综上所述，测地距离不仅可以通过保距性来提高对应准确率，而且可以用于计算局部特征作为一致性对应的约束. 以测地空间作为随机游走求解的约束条件，将三维动态曲面对准问题转化为图的可靠性节点选择问题. 通过马尔可夫模型的快速收敛性和稳定性，提高实现求解.

对于给定的三维动态曲面序列，在任意相邻两帧模型 ${S_k},{S_{k + 1}}$的表面进行均匀采样，得到相应的特征点集：

( $\begin{array}{l} {V^{{S_k}}} = \{ v_1^{{S_k}}, \cdots, v_i^{{S_k}}, \cdots, v_a^{{S_k}} ,\cdots ,v_{{N_k}}^{{S_k}}\}, \\ {V^{{S_{k + 1}}}} = \{ v_1^{{S_{k + 1}}}, \cdots ,v_j^{{S_{k + 1}}}, \cdots, v_b^{{S_{k + 1}}} ,\cdots ,v_{{N_{k + 1}}}^{{S_{k + 1}}}\} . \end{array} $

最优等距映射可以采用下式定义：

1) $A\left( \xi \right) = \frac{1}{{\left| \xi \right|}}\sum\limits_{} {\left| {f(v_i^{{S_k}},v_a^{{S_k}}) - f(v_j^{{S_{k + 1}}},v_b^{{S_{k + 1}}})} \right|} {\kern 1pt} \;.$

式中：f为表面距离相关的函数，例如测地距离、热核距离等，用以保证姿态变化下的距离稳定性. ${a_{ia}} = \left( {v_i^{{S_k}},v_a^{{S_{k + 1}}}} \right)$和 ${a_{jb}} = \left( {v_j^{{S_k}},v_b^{{S_{k + 1}}}} \right)$属于对应集合 $\xi $中的任意2个匹配对. 上述函数用于保证对应结果在距离空间中的分布具有一致性. 对于式（1）的优化是一个NP-hard问题. Sahillioğlu等^[16]采用极大似然估计方法，根据等距性进行迭代优化. 这种优化方法需要不停地循环迭代来减少等距误差. 本文目标是采用测地距离定义亲密度矩阵，通过时空约束定义匹配图节点，将三维动态曲面最小等距性转化为图的可靠性节点选择问题. 利用随机游走的算法进行迭代优化，避免局部收敛问题. 实验结果表明，和已有算法相比，该算法能够更好地得到对应的结果.

该算法的整体流程如图1所示. 对于输入的三维动态曲面序列，该算法对相邻2帧数据执行如下的迭代对准流程，直至得到全部帧的对准结果. 1）对帧数据通过均匀表面采样，得到离散采样点集合. 2）采用这2个点集得到乘积空间，形成候选匹配对. 根据两帧数据采样点之间的时空近邻性裁剪大量候选匹配对，缩小求解空间. 3）对任意2个候选匹配对之间采用测地距离定义边代价，形成随机游走图. 4）通过马尔可夫理论完成约束求解，得到2帧数据的对准结果.

为了能够采用随机游走进行约束求解，需要根据相邻2帧的采样点集定义随机游走图. 根据相邻2帧的采样点集合定义一个乘积空间 ${V^{{S_k}}} \times $ $ {V^{{S_{k + 1}}}}$，乘积空间中的每个元素是一个候选匹配对，作为随机游走图的节点.

对乘积空间中的任意2对匹配对 ${a_{ia}}$和 ${a_{jb}}$之间的关联度进行等距约束，定义匹配对之间的等距约束关联度：

(2) $f({a_{ia}},{a_{jb}}) = \exp \left[ { - {{\left| {g\left( {v_i^{{S_k}},v_j^{{S_k}}} \right) - g\left( {v_a^{{S_{k + 1}}},v_b^{{S_{k + 1}}}} \right)} \right|}}\Big/{c}} \right]\;.$

式中： $g$为模型表面两点之间的测地距离， $c$为常量. 根据式（2）可知，关联度越大，则匹配对之间的等距性越好，匹配对的可信度越高. 对于定义的随机游走图，节点之间边的权重即为匹配对之间的关联度，表明了2个候选匹配对的测地一致性.

定义矩阵 ${{x}} \in {\left[ {0,1} \right]^{{n^V}}}$来表示对应结果，其中 ${n^V} = \left| {{V^{{S_k}}} \times {V^{{S_{k + 1}}}}} \right|$，设置当匹配对 ${a_{ia}}$可靠时 ${{{x}}_{ia}} = 1$（否则为0）. 根据边权重构造关联度矩阵 ${{W}}$：它的对角元素为0，非对角线元素为2个节点的边权重. 在上述 ${{x}}$和 ${{W}}$约束下，最优等距对应问题可以转化为如下二次规划问题：

(3) $\left.\begin{array}{l} \;{{{x}}^*} = \arg \max \left( {{{{x}}^{\rm{T}}}{{W}}{{x}}} \right); \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;{{x}} \in {\left[ {0,1} \right]^{{V^{{S_k}}} \times {V^{{S_{k + 1}}}}}},\;\; \\ \forall i\;\displaystyle\sum\limits_{a = 1}^{{V^{{S_{k + 1}}}}} {{{{x}}_{ia}} \leqslant 1} ,\;\;\forall a\;\displaystyle\sum\limits_{i = 1}^{{V^{{S_k}}}} {{{{x}}_{ia}} \leqslant 1} \;. \\ \end{array}\right\} $

式（3）的约束条件有如下含义： ${V^{{S_k}}}$最多只能找到 ${V^{{S_{k + 1}}}}$中的一个对应点.

对于三维动态曲面的2个相邻帧，可以根据采样点之间的时空相邻性,减少候选匹配对数量. 对于第k帧上的一个顶点，在时空约束下只和第k+1帧的部分顶点构成候选匹配对. 通过下式计算它们的时空相邻性：

(4) $G\left( {v_u^{{S_k}},v_v^{{S_{k + 1}}}} \right){\rm{ = }}\exp \left( { - \frac{{{{\left\| {D\left( {v_u^{{S_k}},v_v^{{S_{k + 1}}}} \right)} \right\|}^2}}}{{{\sigma _2}}}} \right)\;.$

式中： $D\left( {v_u^{{S_k}},v_v^{{S_{k + 1}}}} \right)$为2个特征点之间的欧氏距离. 通过定义的阈值 ${T_{\rm{r}}}$，利用该算法可以过滤掉大量的候选匹配，对随机游走图中的节点进行裁剪，减少矩阵 ${{W}}$的维度.

在图构造过程中，需要从模型表面得到采样点. 采用均匀紧密采样. 在三维模型表面随机取一个点作为初始采样点，以该采样点为中心点，r为半径，标记其范围内区域中所有的顶点. 从未标记的顶点中随机选择一个新的顶点作为采样点. 重复上述过程，直到区域内没有未被标记过的顶点.

根据下式定义采样半径：

(5) $r = 0.17 \times \sqrt {{A}/{\text{π}}} \;.$

式中：A为三维模型表面的曲面面积之和.

根据经典随机游走理论可知，随机游走模型需要对随机矩阵进行归一化处理. 该算法定义下式：

(6) ${d_i} = \sum\nolimits_j {{{{W}}_{ij}}} \;.$

式中：j表示与当前节点i有连接关系的图节点索引， ${d_i}$为随机游走图中节点i到其他所有节点的关联度之和. 传统的归一化方法将随机矩阵中的第i行标准化为 $1/{d_i}$，即保证在每个元素非负的情况下，行元素和为1. 在曲面对准中，将关联度归一化会加大错误匹配的作用，影响随机游走的收敛性. 该算法根据吸收马尔科夫链理论^[17]，引入附加节点 ${v_{{\rm{add}}}}$，吸收每个节点的权重 ${d_{\max }} - {d_i}$，其中定义 ${d_{\max }}$为 ${d_i}$的最大值.

(7) ${d_{\max }} = {\max _i}\;{d_i}\;.$

通过加入附加节点，使得每个节点出度的权重之和为 ${d_{\max }}$，以 $1/{d_{\max }}$进行归一化，保证了弱权边的权重在全局的概率比不变，不会影响随机游走的结果. 构造如下随机游走模型：

(8) $\left.\begin{array}{l} {{P}} =\left[ {\begin{array}{*{20}{c}} {{{W}}/{d_{\max }}}&{{{1}} - ({d}/{d_{\max }}){\bf{1}}}\\ {{{{0}}^{\rm{T}}}}&{{{1}}} \end{array}} \right],\\ \left( {{{{x}}^{\left( {n + 1} \right){\rm{T}}}}\;\;{{x}}_{{\rm{add}}}^{\left( {n + 1} \right)}} \right) = \left[ {{{{x}}^{\left( n \right){\rm{T}}}}\;\;{{x}}_{{\rm{add}}}^{\left( n \right)}} \right]{{P}}\;{\rm{.}} \\ \end{array} \right\}$

式中： ${{{x}}^{\left( n \right)}}$为n时刻游走到各节点的概率. 由于随机游走至附加节点的概率 ${{x}}_{{\rm{add}}}^{}$对匹配结果没有影响，上述模型可以简化为

(9) $ {{P}} = {{W}}/{d_{\max }},\;\;{{{x}}^{\left( {n + 1} \right){\rm{T}}}} = {{{x}}^{\left( n \right){\rm{T}}}}{{P}}\;. $

曲面对准的结果应是一对一映射，上述模型在随机游走过程中没有对此作出约束. 采用个性化PageRank^[18]，对随机游走进行加权调整：

(10) $\;{{{x}}^{\left( {n + 1} \right){\rm{T}}}} = \alpha {{{x}}^{\left( n \right){\rm{T}}}}{{P}} + \left( {1 - \alpha } \right){{{r}}^{\rm{T}}}\;.$

式（10）的含义是使随机游走的过程中，节点每次都有 $\alpha $的概率随着边进行转移，同时 $1{\rm{ - }}\alpha $的概率直接跳转至指定的节点. 通过调整向量 ${{r}}$，可以为上述随机游走模型添加一对一的映射约束. 采用Sinkhorn双随机归一化方法进行调整. 当达到准稳态分布 ${\bar {{x}}}{\rm{ = }}{{\bar {{x}}}^{\left( n \right)}}{\rm{ = }}{{\bar {{x}}}^{\left( {n{\rm{ + }}1} \right)}}$时，随机游走收敛. 采用贪心算法对 ${\bar {{x}}}$进行离散化处理，得到最终的对准结果.

为了验证提出的三维动态曲面对准算法，对算法进行实验分析. 讨论采样频率对结果的影响. 针对DFAUST数据库^[19]、SCPA数据库^[20]和MVPS数据库^[21]进行实验和分析. 其中DFAUST数据库使用定制的多相机系统，捕获人体动态序列. 所有被捕获的人都穿着紧身衣. 对每个捕获的序列进行后处理，保证三维动态曲面的流形结构和拓扑一致性. 与DFAUST数据库相比，SCPA数据库更加复杂，主要是运动的复杂度增加，衣服不再局限于紧身衣，从而使得局部特征变化更明显. 例如StreetDance序列的被捕获者穿着宽松的服装，表演快速而复杂的街舞动作. SCPA采用后处理技术对网格进行处理，保证三维动态曲面的流形结构和拓扑一致性. MVPS数据库是3个数据库中最具有挑战性的，原因如下. 1) 每帧的拓扑结构是不同的. 拓扑一致性对于许多算法很重要，例如基于变形的跟踪. MVPS数据库中的模型无法保证拓扑结构一致性，甚至不能保证每一帧的流形是相同的. 2) 这些数据不仅具有较大的变形，而且遮挡较严重. 将本文算法与如下5种典型的匹配算法相比较：KM算法^[9]、RAVAC算法^[3]、CCM算法^[7]、LRST算法^[1]、GMDSA算法^[13]. 前3种算法用于一般的非刚性对应问题，后2种算法专门用于解决动态曲面对准问题. 为了简化描述，采用IRWG代表本文算法. 对于前2个数据库，采用测地误差用于评估不同的算法. 对于第3个数据库不存在基准对应关系，采用等距误差进行评估.

采样频率的设置会影响对准精度和算法效率. 对不同采样频率得到的结果进行实验比较. 可以发现，随着采样频率的增加，算法精度只有微小的提高，但是匹配时间因为矩阵规模的增加呈指数上升. 考虑到150个采样点能够均匀覆盖到曲面表面，而且没有特别明显的运行时间增加. 采用150个采样点来完成对准. 图2、3分别给出采样频率对算法精度和运行效率的影响. 图中， ${N_{\rm{s}}}$为采样点个数，C为匹配准确度，T为运行时间.

图4给出150个采样点在不同帧上的分布效果. 可以发现，150个采样点已经能够均匀地覆盖整个三维模型表面，保证得到的对准关系能够应用于后续三维动态重建问题.

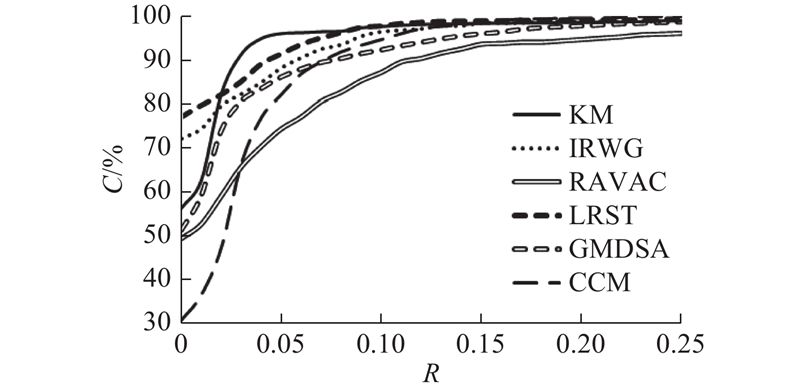
由于DFAUST数据库具有相同的拓扑结构，采用测地误差来度量不同算法的准确性^[22]. 如图5所示为不同算法的测地误差. 图中，R为相似度阈值. 从图5可以看出，对于DFAUST数据库，由于数据具有流形结构，拓扑结构完全一致，各算法均可以得到较好的结果. 其中，利用本文算法IRWG、KM算法和LRST算法得到了较高的精确度. 与IRWG、KM算法相比，提出的IRWG算法的精度稍差，特别是在算法测地线误差较小的时候. 主要原因是DFAUST数据库具有如下特点：拓扑结构完全一致（顶点数和网格数完全一致）、局部特征变化不明显、两帧之间姿态变化不明显. 对于这类数据，KM算法因为通过2帧数据的正定热核矩阵来完成对准. 注意到正定热核矩阵是一种对拓扑和局部特征变化敏感的局部信号描述符. 对于拓扑结构完全一致的三维数据，正定热核矩阵分布具有非常高的一致性，局部特征变化不明显，从而保证KM算法得到了高准确率. LRST算法采用迭代变形拟合相邻两帧三维数据，最终达到变形误差最小化，因此得到了非常高的精度. 本文算法采用测地距离作为约束条件，通过随机游走来完成约束求解. 由于测地距离受形变影响会产生变化，在局部对准精度上没有这2种算法高. 本文算法可以考虑在已有对准基础上，通过ICP变形优化进一步提高对准精度.

如图6所示为各算法可视化的对准结果. 为了方便理解，不同采样点之间的对应采用不同的颜色表示. 从图6可以看出，该算法在不同姿势的模型上保持了较好的鲁棒性.

对于第2个SCPA数据库，由于捕捉对象穿着宽松的衣服且动作幅度较大，对三维模型表面特征和测地距离有比较明显的影响. 如图7所示为不同算法的测地误差. 可以看出，GMDSA、RAVAC、CCM算法的匹配准确性出现了明显的降低. 此外，这类数据会导致部分算法出现明显的对称性问题. 对称性问题主要是由于局部描述符无法区分模型对称部分之间的差异，例如人体的左手和右手. 对于穿着宽松衣服和运动幅度较大的数据，该问题更明显. 图8的第3行显示了对应中的对称性问题，RAVAC算法的匹配结果使得部分数据帧左、右手臂部分出现对称性错误. 由于该数据库具有拓扑和流形一致性，LRST算法和KM算法具有较高的准确性. KM算法由于宽松衣服对模型表面特征的影响，和第1个数据库相比，出现了明显的准确率下降.

对于第3个数据库，数据不能完全保证流形和拓扑的一致性. 这类数据在实际扫描情况中是最普遍的. 对于前面2个数据库，模型具有完全一致的拓扑结构，而且十分完整. 这种数据在实际情况中不具有一般性. 在实际情况中，捕获的动态数据通常会存在大量的噪声和遮挡关系，因此获得的三维动态曲面序列的顶点拓扑是不一样的，而且噪声和空洞使得测地距离没有全局一致性. 可以发现，KM算法尽管在前面2个数据取得非常好的对准结果，但是该算法非常依赖于拓扑的一致性. 对于这类拓扑不一致的数据，利用KM算法生成的热核正定矩阵无法得到精度较高的匹配结果. CCM算法使用的波核信号描述符，对于模型表面噪声和拓扑变化十分敏感，因此对应结果的错误率很高. 利用RAVAC算法计算得到的对准关系，因为依赖于数据的全局测地距离一致性，导致精确度很低. LRST算法的结果较前几种算法稍好，因其使用时空最邻近点作为迭代过程的初始匹配问题. 图9给出动作变化大的2帧数据所得到的对准结果. 可以发现，对于这种高噪声残缺数据，若动作变化过大，则会导致跟踪算法失败. 图9中，对于姿态变化明显的手臂部分，由于手臂和身体部分过于靠近，导致跟踪算法失败. 手臂部分点对准到身体部分（见图9（a））；该算法通过等距约束，能够得到正确的结果（见图9（b））. 对于这部分数据，由于拓扑结构的不一致性，无法采用测地误差评价算法质量. 采用等距误差，评估不同算法的对应结果. 如表1所示为不同算法针对不同动态曲面序列的等距误差. 表中，N/A表示论文作者提供的代码出错，无法完成计算. 从表1可以看出，本文的算法表现优于其他算法. 如图10所示为各算法的对准结果.

在8 GB内存的Intel（R）Core（TM）I5-4200H CPU环境下进行实验. 本文算法IRWG在C++和Matlab环境下执行. 如表2所示为不同算法的运行时间. 其中KM算法和CCM算法在Matlab环境下执行，RAVAC算法和LRST算法在C++环境下运行.

从表2可以看出，由于随机游走的快速收敛性，该算法的效率超过了LRST算法，大大优于KM和RAVAC算法. 与CCM算法相比，该算法的效率稍差. 该算法采用多帧数据构造矩阵，通过矩阵分解完成快速求解，大大提高了求解效率. 这是后续工作可以考虑的问题.

提出时空等距随机游走图，提高三维动态曲面的对准结果和效率. 实验结果验证了该方法在模型姿势变化下具有鲁棒性，且优于已有的方法.

目前，针对三维动态曲面对准问题，给出等距随机游走图求解框架. 在后续工作中，可以考虑结合局部特征定义更具有一般意义的模型，使得该算法不仅能够应用于时空动态数据，而且能够解决静态数据的对应问题. 如何根据模型特征自适应选择对准算法，是一个值得深入研究的问题.