浙江大学学报(工学版)

浙江大学学报(工学版), 2020, 54(1): 40-47 doi: 10.3785/j.issn.1008-973X.2020.01.005

机械工程

基于GA-WPT-ELM的6061铝合金表面粗糙度预测

谭芳芳,, 朱俊江, 严天宏,, 高志强, 何岭松

Surface roughness prediction of 6061 aluminum alloy based on GA-WPT-ELM

TAN Fang-fang,, ZHU Jun-jiang, YAN Tian-hong,, GAO Zhi-qiang, HE Ling-song

通讯作者: 严天宏，男，教授. orcid.org/0000-0003-3916-3926. E-mail： thyan@163.com

收稿日期: 2018-12-3  

Received: 2018-12-3  

作者简介 About authors

谭芳芳（1993—），女，硕士生，从事信号处理的研究.orcid.org/0000-0003-2728-9476.E-mail：tff097443@yeah.net , E-mail：tff097443@yeah.net

摘要

为了提高工件表面粗糙度预测的准确性，针对振动信号特征识别和表面粗糙度预测建模时多个参数难以同步优化和人工经验调优误差较大的问题，提出基于遗传算法（GA）的信号特征识别和表面粗糙度预测的优化算法. 对采集的6061铝合金铣削振动信号进行小波包变换（WPT）和多个特征提取，利用GA优化WPT母小波和特征向量；将信号特征向量和表面粗糙度分别作为极限学习机（ELM）的输入和输出，对预测模型训练的同时，利用GA优化ELM隐含层的神经元个数；对训练好的预测模型进行测试. 实验结果表明，通过GA对振动信号识别和表面粗糙度预测的3类参数同步优化，获得了最佳的信号特征和较高的表面粗糙度预测精度，节省了建模分析计算成本.

关键词： 在线振动信号 ; 遗传算法（GA） ; 小波包变换 ; 极限学习机（ELM） ; 表面粗糙度预测

Abstract

The problem of multi-parameter simultaneous optimization and large error of empirical tuning should be solved in the vibration signal feature recognition and surface roughness prediction processes in order to improve the on-line prediction accuracy of workpiece surface roughness. The optimization method of signal feature recognition and surface roughness prediction modeling was proposed based on genetic algorithm (GA). GA was used to choose mother wavelet and feature quantities when signal features of milling 6061 aluminum alloy was recognized based on wavelet packet transform (WPT). The number of neurons in hidden layer was selected by GA when signal features and surface roughness were used to train extreme learning machine (ELM). The prediction modeling which has been trained was tested. The experimental results show that the three types of parameters for signal recognition and surface roughness prediction were simultaneously optimized by GA. GA-WPT-ELM not only obtains the best features of signal and the higher prediction accuracy of surface roughness, but also reduces analytical-computational cost in the modeling processes.

Keywords： on-line vibration signal ; genetic algorithm (GA) ; wavelet packet transform ; extreme learning machine (ELM) ; surface roughness predicting

PDF (1170KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

谭芳芳, 朱俊江, 严天宏, 高志强, 何岭松. 基于GA-WPT-ELM的6061铝合金表面粗糙度预测. 浙江大学学报(工学版)[J], 2020, 54(1): 40-47 doi:10.3785/j.issn.1008-973X.2020.01.005

TAN Fang-fang, ZHU Jun-jiang, YAN Tian-hong, GAO Zhi-qiang, HE Ling-song. Surface roughness prediction of 6061 aluminum alloy based on GA-WPT-ELM. Journal of Zhejiang University(Engineering Science)[J], 2020, 54(1): 40-47 doi:10.3785/j.issn.1008-973X.2020.01.005

在数控机床铣削过程中，工件表面粗糙度直接反映了工件表面质量[1]，是铣削加工中重点控制的产品质量参数. 铣削过程是动态的，铣削用量、工件材料、铣削振动等诸多影响表面粗糙度的因素在不断变化，若仅采用固定的铣削用量，则无法保证加工质量和生产效率[2]. 如果能够实现表面粗糙度的实时在线检测，及时控制加工过程调整铣削用量，则避免了加工过程中原料、人力和时间的浪费. 目前在线检测表面粗糙度的方法主要分为以下2类：1）直接在线检测表面粗糙度如光电检测技术[3-4]，由于机械加工过程必须使用冷却液覆盖工件表面，导致光学实时检测表面粗糙度难以实现；2）通过监测加工状态间接检测工件表面粗糙度，主要利用加工参数或相关物理量，建立与表面粗糙度之间的预测模型[5-7]. 由于复杂多变的加工因素，难以综合铣削参数、材料、刀具等建立准确的预测模型. 通过在线检测相关物理量可以实时计算表面粗糙度，因振动加速度能够准确反映工件表面粗糙度的变化，受机床振动的影响较小，Hessainia等[8-10]将振动加速度作为相关物理量，建立表面粗糙度预测模型.

随着智能算法和传感器技术的发展，通过分析铣削加速度振动信号预测表面粗糙度的方法越来越成熟. 早期，迟军等[11]利用小波包分析振动信号和松散型小波网络，实现表面粗糙度的在线预测. Upadhyay等[12-13]根据时域分析法处理振动信号并结合切削参数，实现表面粗糙度的在线监测. 近期，Plaza等[14]提出在时域用奇异谱分析方法仅通过经验正交函数分析振动信号，监测在线加工的表面粗糙度. 后来，Plaza等[15]提出通过小波包变换(WPT)提取切削力信号特征并预测表面粗糙度，获得了较好的预测结果. 以上研究均未考虑在提取信号特征和表面粗糙度预测操作过程中，同时实现信号最佳特征量的选取和预测模型最优参数的确定，过度依赖人工经验在大量复杂的正交实验中对信号特征量和预测模型参数进行选取匹配，使得建模过程耗时费力且会造成较大的预测误差.

根据以上研究中的不足，本文在正交实验中利用小波包分解法时频域多分辨率的特性提取信号特征，研究将信号特征量作为极限学习机(ELM)预测模型的输入，实现表面粗糙度预测. 利用遗传算法(GA)逐代进化、全局优化的思想，对信号最佳统计特征向量的选取和表面粗糙度预测模型的最优参数进行组合优化选择.

1. WPT提取特征算法和ELM预测模型

1.1. 小波包提取特征算法

小波包分解是针对多分辨率的信号分析方法，在时域和频域都有表征信号局部信息的能力[16-17]. 相比小波分解只对低频部分再分解，小波包对高低频信号均进行再分解，是一种更精细的特征提取方法. 小波基函数 $\varPsi \left( t \right) \in {L^2}\left( R \right)$，将Ψ（t）经伸缩平移后，可以生成小波函数系：

${\varPsi _{a,b}}\left( t \right) = {\left| a \right|^{ -{1}/{2}}}\varPsi \left( {\frac{{t - b}}{a}} \right).$

式中：a为尺度因子，b为平移因子.

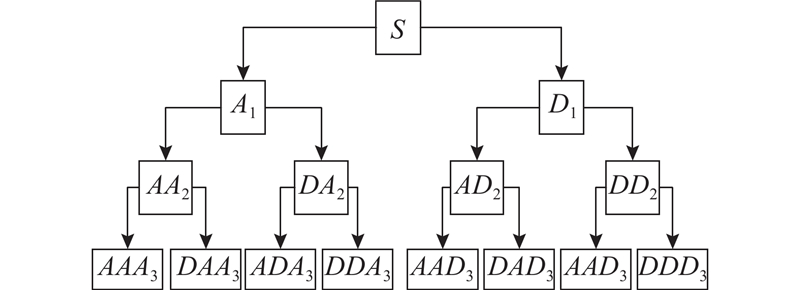
在多分辨率中，设共轭滤波器h（n），定义A0为尺度函数φ（t），D1为小波基函数Ψ（t），令 $g\left( k \right) = {\left( { - 1} \right)^k}h(1 - k)$. 若信号S长度为2N，分解j次，每个频段数据长度变为2N−j，则满足双尺度关系的一列递归分解公式为

$\left. \begin{array}{l} A_{2n}^j\left( t \right) = \displaystyle\sum\limits_k h \left( {k - 2t} \right)A_n^{j - 1}\left( k \right),\\ D_{2n + 1}^j\left( t \right) = \displaystyle\sum\limits_k g \left( {k - 2t} \right)D_n^{j - 1}\left( k \right). \end{array} \right\}$

式中：h、g为一组共轭正交滤波器A、D的滤波系数，A2n（t）为关于正交尺度函数φ（t0）的小波包.

分解后的每个节点均包含关于信号S的低通滤波结果 $A_{2n}^j $、高通滤波结果 $D_{2n+1}^j $分别组成的信号特征. 小波包分解非常适用于局部特性突出的非平稳振动信号处理. 小波包的3层分解示意图如图1所示.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   小波包分解结构图

Fig.1   Structure diagram of WPT


1.2. 极限学习机预测模型

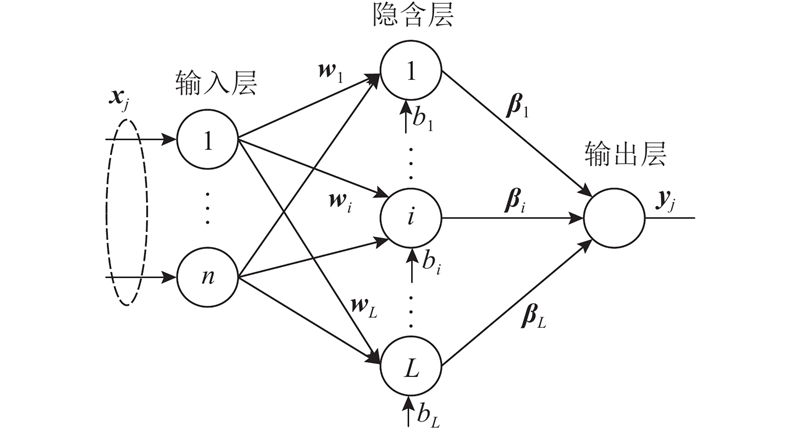
极限学习机是由Huang等[18-19]提出的3层前馈神经网络，输入层与隐含层之间的连接权值wi和隐含层神经元的偏置bi是随机产生且固定的，只须设置隐含层神经元的个数，因此极大地缩短了网络训练时间，提高了泛化性能. 基本的ELM结构如图2所示.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   极限学习机网络结构图

Fig.2   Network structure diagram of extreme learning machine


给定N个训练样本（xj,yj），则ELM数学模型如下：

${f_{l}}({{{x}}_j}) = \sum\limits_{i = 1}^{\tilde N} {{{{\beta}} _i}g\left( {{{w}}_i {{{x}}_j} + {b_i}} \right)} = {{{y}}_j};j = 1,\cdots,N.$

式中：l为隐含层神经元个数，xj为第j个样本输入即信号特征量，yj为样本输出即表面粗糙度， $g({{{w}}_i} {{{x}}_j} + {b_i})$为输出函数. 根据零误差逼近训练样本，由最小二乘法求解式（4），可以求得输出层连接权值β：

$\mathop {\min }\limits_{{\beta}}\; \left\| {{{{H}}_{N \times l}}{{{\beta}} _{l \times m}} - {{T}}_{N \times m}} \right\|.$

式中：T为网络输出，H为隐含层输出矩阵. 选取合理的l，可以有效减小求解β时的计算量和训练误差.

2. 基于GA-WPT-ELM表面粗糙度预测

2.1. 遗传算法

遗传算法是一种自然进化模型[20-21]，它是根据自然界优胜劣汰、适者生存的法则，产生由遗传算子组成的初始种群，进行选择、复制、交叉、变异等反复优化操作. 对需要优化的个体进行编码，设置适应度函数对新的个体的优劣进行评价，直至获得满足要求的最优解. GA算法具有不需要求梯度、全局优化时可并行处理等优点，可以自适应地在问题域进行随机搜索，即可在许多局部较优中找到全局最优解，能够有效处理复杂的组合优化问题[22-24].

2.2. GA-WPT-ELM优化方法设计

对振动信号特征提取方法和表面粗糙度预测方法进行优化设计时，不仅要保证模型可行，而且力求表面粗糙度预测模型的准确性，减少建模时人工盲目选取特征量、调节网络参数时造成的较大偏差，确保预测模型的稳定性. 在小波包分析信号提取特征和极限学习机预测表面粗糙度建模参数优化设计时，信号最佳特征量的选取和表面粗糙度预测模型最优参数求取均是非线性问题，属于多目标优化问题，适合于应用遗传算法求解.

GA对WPT识别由时间振幅组成的振动信号特征时的母小波Ψ、统计特征量v和l这3个参数进行优化，使得优化后的WPT和ELM能够更好地提取有效的信号特征和预测目标函数的输出. GA优化要素包括种群初始化、适应度计算、选择复制、交叉和变异操作. GA的特征提取和表面粗糙度预测的优化方法流程如图3所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   GA优化特征提取和预测模型的流程图

Fig.3   Optimization method flowchart of feature extraction


GA-WPT-ELM预测表面粗糙度的操作步骤如下.

1）种群初始化. 将WPT提取信号特征和ELM预测表面粗糙度网络结构的参数视为优化目标. 每个个体均为一个实数串，由3个待优化参数组成：Ψ、v、l.

2）设定GA优化运行参数：初始群体规模为50×3=150，交叉概率Pc=0.8，变异概率Pm=0.02.

3）编码. 由于二进制编码计算量大且精度不高，采用精度高搜索空间更大的十进制编码[25]，Ψ∈[1,40]，vr∈[1，2j]（其中j为小波包分解层数，共2j个频段，vr表示特征向量均值、标准差、峰峰值、偏态、峰态、能量熵之一），l∈[1,300]，组成一个实数编码个体（Ψ，v，l）.

4）适应度计算. 通过适应度函数计算种群适应度，可以将提取的振动信号统计特征量作为ELM预测模型的输入，表面粗糙度Ra作为网络输出来训练ELM网络；用训练好的网络进行预测，测量Ra和预测 ${\hat R_{\rm{a}}}$的平均相对误差的倒数fi（x）设计为适应度函数，如下：

${f_i}\left( x \right) = 1\Bigg/\left( {1 + h + \frac{1}{N}\sum\limits_{i = 1}^N {\left| {\frac{{{R_{{\rm{a}}i}} - {\hat R_{{\rm{a}}i}}}}{{{R_{{\rm{a}}i}}}}} \right|} } \right);\;h \geqslant 0.$

$x = \left[ {\varPsi ,v,l} \right] \in S \subset X.$

式中：h为目标函数保守估计的边界值，N为ELM输出层的节点数，S为优化参数Ψ、v、l构成的解空间.

5）选择操作. 根据适应度函数的平均相对误差最小化，计算选择概率 ${p_i} = {f_i}/\sum\nolimits_{i = 1}^n {{f_i}} $（其中n为初始种群总数），选择适应度最高的个体.

6）交叉操作. 由于个体编码为十进制实数编码，采用实数交叉法，从种群中选择2个个体，按概率Pc=0.8交叉得到新个体.

7）变异操作. 任选种群中的1个个体，对染色体按概率Pm=0.02进行变异操作.

8）种群更新. 对新一代种群循环以上操作，不断提高群体适应度，直到最新种群满足GA优化条件，继续执行下一步. 若不满足，则返回执行步骤4）.

9）解码最优个体，获得最优WPT母小波、统计特征值和ELM隐含层神经元个数.

10）误差计算. 将最优统计特征量vrk（第k组信号）和表面粗糙度Rak（第k个测量值）作为训练ELM的输入和输出，计算ELM模型预测 ${\hat R_{\rm{a}}}$和测量Ra的平均相对误差，并更新下式输出权值β：

${f_{l}}\left( {{{{v}}_{{\rm{r}}k}}} \right) = \sum\limits_{i = 1}^{l} {{{{\beta}} _{i}}} g\left( {{{{w}}_{i}} {{{v}}_{{\rm{r}}k}} + {b_i}} \right) = {{{R}}_{{\rm{a}}k}};\;k = 1, \cdots ,N.$

11）直到ELM网络训练误差满足期望，确定预测模型并输出测试样本的表面粗糙度预测值 ${\hat R_{\rm{a}}}$.

3. 实验设计

铣削加工实验选用材料6061铝块，使用三轴振动加速度传感器，采集工件不同振动方向（Gx、Gy、Gz）的同源信号. 为了准确获取动态振动信号，将传感器放置在尽可能接近工件刀具的接触区域，采样频率设置为12 800 Hz. 实验中选用80个工件，分别采集x、y、z方向信号，共960组数据，再由 Coinv DASP-V11智能信号采集处理分析仪采集，作为数据文件存储在计算机的硬盘中，使用Matlab软件对数据进行分析，如图4所示. 设计不同的铣削加工参数切削速度n、进给量d、侧吃刀量f进行正交试验，如表1所示.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

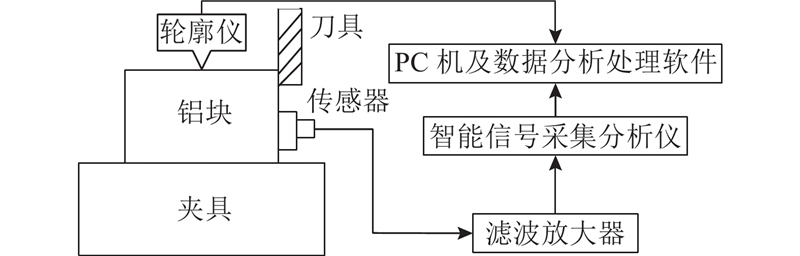
图 4   铣削振动信号采集与分析系统

Fig.4   Signal acquisition and analysis system of milling vibration


表 1   铣削加工参数

Tab.1  Milling parameters

n/（103 r·min−1） f/（103 mm·min−1） d/mm
6 1 1.0
9 1.65 0.7
12 2.3 0.5
15 3 0.3
18 — —

新窗口打开| 下载CSV


当利用粗糙度轮廓仪测量工件的表面粗糙度时，为了提高实验数据的可靠性，将工件表面分为4个等距采样区域（D1、D2、D3、D4），如图5所示，D1和D4为靠近卡盘端口的工件两侧区域，D2和D3为工件的中心区域. 为了减小个别样本偏差较大造成的实验误差，选用4个区域测量值Ra的算数平均值，作为实验样本数据. 对振动信号和工件表面粗糙度产生一些不能代表信号信息的突变点加以剔除. 实验中，随机选取数据集的75%作为预测模型的训练样本，其余25%作为模型验证样本.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   主轴铣削实验及传感器测量

Fig.5   Spindle milling experiment and sensor measurement


4. 实验仿真及分析

4.1. GA优化参数初始化

GA在振动信号特征提取和表面粗糙度预测方法优化时，须对以下参数初始化. 1）信号特征提取时基于小波包分析的40种母小波Ψ，如表2所示. 2）小波包提取的6种统计特征量v：均值、标准差、峰峰值、偏态、峰态、能量熵，如表3所示. 表中，λi表示WPT对应层的节点，Gj表示工件x、y、z方向的振动信号. 3）表面粗糙度预测方法ELM的隐含层神经元个数l，设定范围为[1，300]. 当利用GA优化多个参数时，分别对Ψ、v、l进行实数编码，设定GA训练过程中的参数：初始种群规模为50，进化次数为50，复制适应度的前20%个体，其余80%个体作交叉变异，每次GA寻优时需要完成50×50×4/5=2 000个点的搜索实验.

表 2   小波包分解的母小波类型

Tab.2  Mother wavelets of wavelet packet decomposition

类型 族系 Ψ
正交 Daubechies db2,db3,db4,db5,db6,db7,db8,db9,
db10,db11,db12,db13,db14
正交 Haar Haar
正交 Coiflets coif1,coif2,coif3,coif4,coif5
正交 Symmlets sym2,sym3,sym4,sym5,sym6,sym7, sym8
双正交 Biorthogonal bior1.3,bior1.5,bior2.2,bior2.4,bior2.6,
bior2.8,bior3.1,bior3.3,bior3.5,bior3.7,
bior3.9,bior4.4,bior5.5,bior6.8

新窗口打开| 下载CSV


表 3   振动信号的统计特征量

Tab.3  Statistical feature extraction of vibration signals

特征 v 特征 v
均值 $J_{_{Gj}}^{{\lambda ^i}}$ 偏态 $P_{_{Gj}}^{{\lambda ^i}}$
标准差 $B_{_{Gj}}^{{\lambda ^i}}$ 峰态 $F_{_{Gj}}^{{\lambda ^i}}$
峰峰值 ${\rm{FF}}_{_{Gj}}^{{\lambda ^i}}$ 能量熵 $H_{_{Gj}}^{{\lambda ^i}}$

新窗口打开| 下载CSV


4.2. GA优化特征提取和预测模型参数结果分析

为了定量评价GA-WPT-ELM算法的预测性能，将表面粗糙度测量值Rai与预测值 ${\hat R_{{\rm{a}}i}}$的平均相对误差

${\bar e_{\rm{r}}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{R_{{\rm{a}}i}} - {\hat R_{{\rm{a}}i}}}}{{{R_{{\rm{a}}i}}}}} \right|} \times 100 \text{%}$

作为预测模型的评估指标，预测精度 $\sigma = 1 - {\bar e_{\rm{r}}}$，其中n为表面粗糙度总个数.

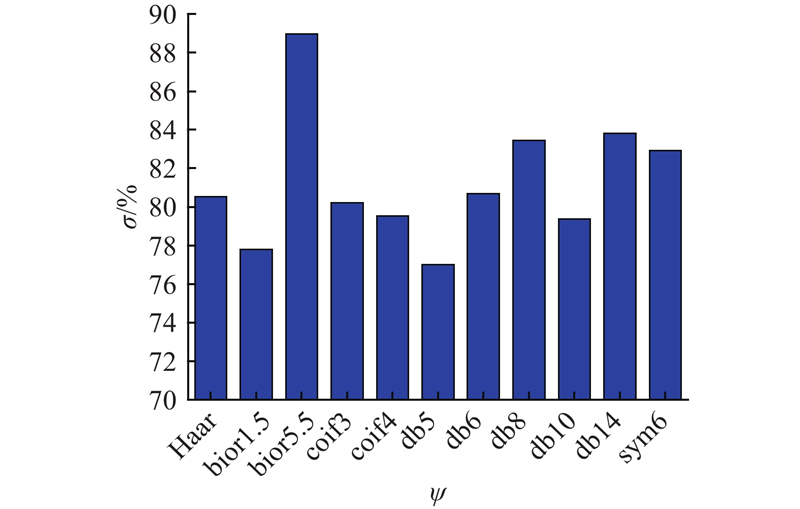
4.2.1. 母小波优化结果

选择Gx振动信号作5层WPT分解，全局中满足GA优化目标的母小波部分选择结果如图6所示. 母小波Ψ的选取结果有正交型和双正交型，说明输入不同的振动信号，GA优化法会根据实际信号的特点，从母小波库中选择匹配信号振荡特性的最优母小波，实现对应信号特征的准确识别. 从图6可以看出，当优化选取对不同尺度伸缩且具有双正交性的母小波‘bior5.5’，将其用于小波包分解，可以有效地提取信号特征趋势项，所得表面粗糙度的预测精度σ最高为88.95%. 相应的‘bior5.5’的分解尺度函数φ和小波函数ϕ如图7所示. 图中，ni为小波基近代计算的迭代次数.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   母小波优化选取结果

Fig.6   Optimization results of mother wavelets


图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   bior5.5的尺度函数和小波函数

Fig.7   Scale function and wavelet function for mother wavelet bior5.5


4.2.2. 特征提取结果

从表4可以看出，GA优化选取的不同统计特征量v对表面粗糙度预测精度σ的影响程度明显不同，其中小波包能量熵向量作为样本输入的训练效果最佳. 对比分析Gx轴向与Gy、Gz轴向的选取结果可知，能量熵 $H_{G_x}^{{\rm{DAAAA}}}$的预测误差最小，是最具表征性的统计特征量. 基于GA优化的特征提取方法不仅在WPT多层分解和统计特征量多样的情况下，能够选取到最具表征性的特征向量，使得预测精度σ=88.95%，而且可以根据小波包分解的多节点时频域能量分布特点，提取最有效的信号振荡趋势变化的节点能量熵.

表 4   GA优化算法训练结果

Tab.4  Training results of GA options algorithm

振动信号组别 Ψ v l σ/%
Gx bior5.5 $H_{G_{x}}^{\rm{DAAAA}}$ 76 88.95
Gx db8 $H_{G_{x}}^{\rm{DAAA}}$ 62 83.46
Gx Haar $P_{G_{x}}^{\rm{DAD}}$ 49 80.53
Gx coif3 $F_{G_{x}}^{\rm{DADAA}}$ 96 80.22
Gy db14 $H_{G_{y}}^{\rm{ADA}}$ 86 83.82
Gy db5 $H_{G_{y}}^{\rm{ADAA}}$ 64 82.22
Gy bior1.5 $H_{G_{y}}^{\rm{AAADA}}$ 31 81.24
Gz db6 $H_{G_{z}}^{\rm{AADAD}}$ 26 80.69
Gz sym6 $H_{G_{z}}^{\rm{DADA}}$ 38 82.92

新窗口打开| 下载CSV


4.2.3. 神经元个数优化结果

根据实验设定的样本数量和ELM隐含层的神经元个数l范围[1，300]，结合表4中GA优化结果可以看出，当l=76时预测精度最高即σ=88.95%，此时l小于设定的训练集样本数320×75%= 240，符合零误差逼近训练样本原则. 因此GA优化l时，ELM不仅综合了训练集和测试集预测率折中选择l来匹配网络隐含层节点数，而且利用最小二乘法和零误差逼近原则求解得到网络输出层的权值β，确保ELM网络输出误差最小，避免了人为设定l对预测结果造成的较大误差.

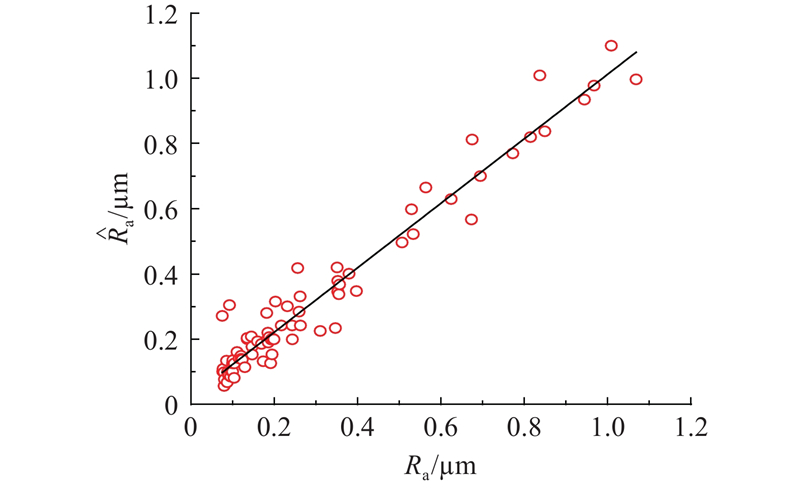
4.3. 基于GA-WPT-ELM表面粗糙度预测结果分析

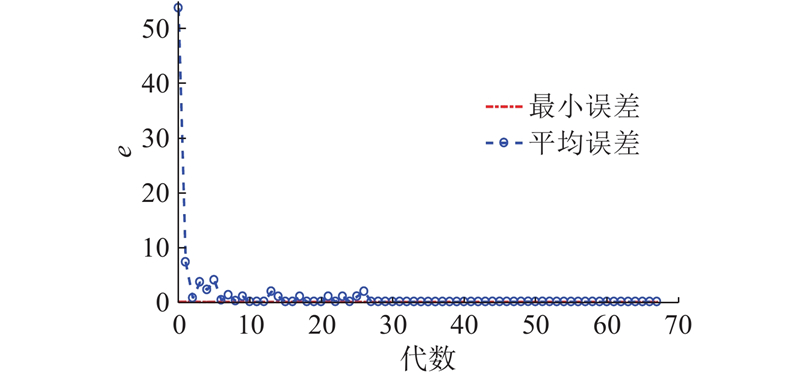
GA优化训练过程如图8所示，个体逐代进化到第27代时GA的训练误差e趋于平稳，直至进化到67代，当前个体计算所得的适应度满足终止条件. 训练曲线体现了GA的搜索能力和优化机制，丰富的动态特性使得种群进化很快进入自适应优化过程，实现信号特征提取和预测模型组合优化库的参数搜索任务. 结合表4可以看出，对于每组不同的振动信号，对应GA优化选取的3个个体所预测的表面粗糙度精度差异明显. 其中适应度最高的个体解码得到的母小波Ψ为bior5.5、统计特征量v为 $H_{_{G_x}}^{{\rm{DAAAA}}}$和ELM隐含层神经元个数l为76，预测精度最高为88.95%，可见GA优化预测方法具有实际可行性. 优化结果表明，GA参数寻优结果与获取振动信号的方向密切相关，应优先选择Gx组信号，以提高预测精度.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   GA优化曲线及个体选择

Fig.8   Optimization curve and individual selection of GA


${\hat R_{\rm{a}}}$和Ra的对比结果如图9和表5所示. 针对正交实验中Gx组数据集的25%的测试样本，根据WPT提取的信号统计特征量，结合ELM预测模型的分析能力， ${\hat R_{\rm{a}}}$与Ra之间的调节决定系数R2adj为0.950 5，表现出较好的拟合优度和相关性. 表5列出20组振动信号表面粗糙度的预测值，误差Δe为[−0.049 5 μm，0.069 3 μm]，平均误差仅为0.003 9 μm，本文的分析模拟值非常接近实际值，体现了该预测模型的准确性和可靠性，对解决类似非线性信号的特征提取和预测建模问题具有一定的适用性.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   表面粗糙度拟合曲线

Fig.9   Fitting curve of surface roughness


表 5   表面粗糙度预测结果

Tab.5  Prediction results of surface roughness

组序号 n/（103
r·min−1） 		f/（103
mm·min−1） 		d/
mm 		$ \hat R_{\rm{a}} $/μm Ra/μm Δe/
μm
1 18 1.65 0.3 0.122 8 0.137 1 0.014 4
2 12 1.65 0.3 0.146 3 0.176 9 0.030 7
3 15 2.3 0.3 0.173 0 0.132 4 −0.040 6
4 6 1 1.0 0.187 5 0.206 5 0.019 0
5 12 2.3 1.0 0.216 5 0.242 2 0.025 7
6 15 3 1.0 0.262 5 0.242 2 −0.020 3
7 9 2.3 0.5 0.350 5 0.419 8 0.069 3
8 12 3 0.3 0.356 3 0.367 6 0.011 4
9 9 2.3 0.7 0.396 8 0.347 3 −0.049 5
10 6 1.65 0.5 0.506 5 0.496 5 −0.010 0
11 9 3 1.0 0.624 0 0.629 7 0.005 7
12 9 3 0.5 0.694 3 0.700 2 0.005 9
13 6 2.3 1.0 0.772 3 0.770 0 −0.002 2
14 6 2.3 0.5 0.849 3 0.837 5 −0.011 8
15 6 3 0.5 0.967 3 0.977 9 0.010 6

新窗口打开| 下载CSV


4.4. 对比讨论

表6对目前振动分析方法应用研究结果作了比较. Risbood等[13]根据时域分析法处理振动信号并结合切削参数作为预测模型的输入，样本极少且预测精度不高. Plaza 等[14]通过奇异谱分析对振动信号进行特征提取及表面粗糙度预测，但是奇异谱分析本身复杂的矩阵计算限制了在线预测的实时性需求. Plaza等[15]研究WPT提取切削力信号特征向量，获得了较好的预测精度，但未考虑提取最优统计特征量选取对人工经验依懒性强的问题，增加了实际在线加工检测成本. 本文方法是基于模式识别和GA全局优化思想对特征提取和预测模型进行优化，解决了上述文献特征识别、预测网络训练过程人工盲目优化参数的问题.

表 6   不同研究方法的表面粗糙度预测结果对比

Tab.6  Comparison of surface roughness prediction results for different methods

比较对象 信号源 样本数 方法 v σ/%
本文研究 振动信号 960 GA-WPT $H_{G_{x}}^{\rm{DAAAA}}$ 88.95
文献[14] 振动信号 360 SSA $a_y^{{\lambda _i}}$ 85.4
文献[13] 振动信号 20 TDA ax, v,f,d 80.0
文献[15] 切削力信号 360 G-WPT $X_{{F_X}}^{\rm{AAAA}}$ 88.1

新窗口打开| 下载CSV


5. 结　论

（1）提出基于GA优化的铣削振动信号WPT特征提取法和工件表面粗糙度ELM预测方法. 通过计算组合参数的适应度不断自适应调优，GA-WPT-ELM算法不但提取了振动信号在时频域中的多个统计特征参数，实现了表面粗糙度的精确预测，而且解决了在正交实验中特征向量和预测网络参数确定时的盲目性以及反复调优的难题.

（2）利用GA-WPT-ELM优化算法明显提高了针对信号特征预测表面粗糙度的效率和准确性，节省了在线检测系统的分析时间和成本，克服了传统离线检测表面粗糙度由于加工环境和人工经验造成的较大误差和检测效率不高等缺陷，为在线加工的实时检测系统的实现提供了有效的解决方法.

（3）振动信号特征识别和表面粗糙度预测方法的精确性和计算效率还有很大的优化空间，是后续智能化的表面粗糙度在线检测方法的重点研究方向.

参考文献

WANG H, TO S, CHAN C Y

Investigation on the influence of tool-tip vibration on surface roughness and its representative measurement in ultra-precision diamond turning

[J]. International Journal of Machine Tools and Manufacture, 2013, 69 (3): 20- 29

[本文引用: 1]

仲为武, 赵东标, 王希

航空铝合金7050-T7451干式铣削工艺参数对振动信号影响研究

[J]. 中国机械工程, 2011, 22 (4): 458- 461

[本文引用: 1]

ZHONG Wei-wu, ZHAO Dong-biao, WANG Xi

Effects of process parameters on vibration signals in dry milling of aeronautic aluminum alloy 7050-T7451

[J]. China Mechanical Engineering, 2011, 22 (4): 458- 461

[本文引用: 1]

王政平, 张锡芳, 张艳娥

表面粗糙度光学测量方法研究进展

[J]. 传感器与微系统, 2007, 26 (9): 4- 6

DOI:10.3969/j.issn.1000-9787.2007.09.002      [本文引用: 1]

WANG Zheng-ping, ZHANG Xi-fang, ZHANG Yan-e

Progress on optical measurement of surface roughness

[J]. Transducer and Microsystem Technologies, 2007, 26 (9): 4- 6

DOI:10.3969/j.issn.1000-9787.2007.09.002      [本文引用: 1]

刘晨, 卢荣胜, 陈磊, 等

基于光学法表面粗糙度的测量研究进展

[J]. 半导体光电, 2010, 31 (4): 495- 500

[本文引用: 1]

LIU Chen, LU Rong-sheng, CHEN Lei, et al

Progress of surface roughness measurement based on optical method

[J]. Semiconductor Optoelectronics, 2010, 31 (4): 495- 500

[本文引用: 1]

SALGADO D R, ALONSO F J, CAMBERO I, et al

In-process surface roughness prediction system using cutting vibrations in turning

[J]. The International Journal of Advanced Manufacturing Technology, 2009, 43 (1/2): 40- 51

[本文引用: 1]

LAURO C H, BRANDAO L C, BALDO D, et al

Monitoring and processing signal applied in machining processes: a review

[J]. Measurement, 2014, 58: 73- 86

DOI:10.1016/j.measurement.2014.08.035     

OZEL T, KARPAT Y, LUÍS FIGUEIRA, et al

Modelling of surface finish and tool flank wear in turning of AISI D2 steel with ceramic wiper inserts

[J]. Journal of Materials Processing Technology, 2007, 189 (1-3): 192- 198

DOI:10.1016/j.jmatprotec.2007.01.021      [本文引用: 1]

HESSAINIA Z, BELBAH A, YALLESE M A, et al

On the prediction of surface roughness in the hard turning based on cutting parameters and tool vibrations

[J]. Measurement, 2013, 46 (5): 1671- 1681

DOI:10.1016/j.measurement.2012.12.016      [本文引用: 1]

KIM D S, CHANG I C, KIM S W

Microscopic topographical analysis of tool vibration effects on diamond turned optical surfaces

[J]. Precision Engineering, 2002, 26 (2): 168- 174

DOI:10.1016/S0141-6359(01)00115-5     

SEGRETO T, KARAM S, SIMEONE A, et al

Residual stress assessment in Inconel 718 machining through wavelet sensor signal analysis and sensor fusion pattern recognition

[J]. Procedia CIRP, 2013, 9: 103- 108

DOI:10.1016/j.procir.2013.06.176      [本文引用: 1]

迟军, 陈廉清, 杨超珍

基于小波包分析和Elman网络的切削表面粗糙度预测方法

[J]. 中国机械工程, 2010, (7): 822- 826

[本文引用: 1]

CHI Jun, CHEN Lian-qing, YANG Chao-zhen

Research on prediction of cutting surface roughness based on wavelet packet analysis and Elman network

[J]. China Mechanical Engineering, 2010, (7): 822- 826

[本文引用: 1]

UPADHYAY V, JAIN P K, MEHTA N K

In-process prediction of surface roughness in turning of Ti–6Al–4V alloy using cutting parameters and vibration signals

[J]. Measurement, 2013, 46 (1): 154- 160

DOI:10.1016/j.measurement.2012.06.002      [本文引用: 1]

RISBOOD K A, DIXIT U S, SAHASRABUDHE A D

Prediction of surface roughness and dimensional deviation by measuring cutting forces and vibrations in turning process

[J]. Journal of Materials Processing Tech, 2003, 132 (1): 203- 214

[本文引用: 3]

PLAZA E G, LÓPEZ P J N

Surface roughness monitoring by singular spectrum analysis of vibration signals

[J]. Mechanical Systems and Signal Processing, 2017, 84: 516- 530

DOI:10.1016/j.ymssp.2016.06.039      [本文引用: 3]

PLAZA E G, LÓPEZ P J N

Analysis of cutting force signals by wavelet packet transform for surface roughness monitoring in CNC turning

[J]. Mechanical Systems and Signal Processing, 2018, 98: 634- 651

DOI:10.1016/j.ymssp.2017.05.006      [本文引用: 3]

钟崴, 彭梁, 周永刚, 等

基于小波包分析和支持向量机的锅炉结渣诊断

[J]. 浙江大学学报: 工学版, 2016, 50 (8): 1499- 1506

[本文引用: 1]

ZHONG Wei, PENG Liang, ZHOU Yong-gang, et al

Slagging diagnosis of boiler based on wavvelet packet analysis and support vector machine

[J]. Journal of Zhejiang University: Engineering Science, 2016, 50 (8): 1499- 1506

[本文引用: 1]

李国宾, 关德林, 李廷举

基于小波包变换和奇异值分解的柴油机振动信号特征提取研究

[J]. 振动与冲击, 2011, 30 (8): 149- 152

DOI:10.3969/j.issn.1000-3835.2011.08.029      [本文引用: 1]

LI Guo-bin, GUAN De-lin, LI Ting-ju

Study on feature extraction of diesel engine vibration signal based on wavelet packet transform and singularity value decomposition

[J]. Journal of Vibration and Shock, 2011, 30 (8): 149- 152

DOI:10.3969/j.issn.1000-3835.2011.08.029      [本文引用: 1]

HUANG G B, ZHU Q Y, SIEW C K

Extreme learning machine: theory and applications

[J]. Neurocomputing, 2006, 70 (1-3): 489- 501

DOI:10.1016/j.neucom.2005.12.126      [本文引用: 1]

HUANG G B, ZHOU H, DING X, et al

Extreme learning machine for regression and multiclass classification

[J]. IEEE Transactions on Systems, Man and Cybernetics, Part B (Cybernetics), 2012, 42 (2): 513- 529

DOI:10.1109/TSMCB.2011.2168604      [本文引用: 1]

段斌, 梁军, 费正顺, 等

基于GA-ANN的非线性半参数建模方法

[J]. 浙江大学学报: 工学版, 2011, 45 (6): 977- 983

[本文引用: 1]

DUAN Bin, LIANG Jun, FEI Zheng-shun, et al

Nonlinear semi-parametruc modeling mothed based on GA-ANN

[J]. Journal of Zhejiang University: Engineering Science, 2011, 45 (6): 977- 983

[本文引用: 1]

刘浩然, 赵翠香, 李轩, 等

一种基于改进遗传算法的神经网络优化算法研究

[J]. 仪器仪表学报, 2016, 37 (7): 1573- 1580

DOI:10.3969/j.issn.0254-3087.2016.07.017      [本文引用: 1]

LIU Hao-ran, ZHAO Cui-xiang, LI Xuan, et al

Study on a neural network optimization algorithm based on improved genetic algorithm

[J]. Chinese Journal of Scientific Instrument, 2016, 37 (7): 1573- 1580

DOI:10.3969/j.issn.0254-3087.2016.07.017      [本文引用: 1]

杨阳, 李春, 缪维跑, 等

基于多目标遗传算法的风力机叶片全局优化设计

[J]. 机械工程学报, 2015, 51 (14): 192- 198

[本文引用: 1]

YANG Yang, LI Chun, MIAO Wei-pao, et al

Global optimal design of wind turbines blade based on multi-object genetic algorithm

[J]. Journal of Mechanical Engineering, 2015, 51 (14): 192- 198

[本文引用: 1]

TABOADA H A, ESPIRITU J F, COIT D W

MOMS-GA: a multi-objective multi-state genetic algorithm for system reliability optimization design problems

[J]. IEEE Transactions on Reliability, 2008, 57 (1): 182- 191

DOI:10.1109/TR.2008.916874     

刘守山, 杨辰龙, 李凌, 等

基于自适应小波阈值的超声信号消噪

[J]. 浙江大学学报: 工学版, 2007, 41 (9): 1557- 1560

[本文引用: 1]

LIU Shou-shan, YANG Chen-long, LI Ling, et al

Adaptive wavelet thresholding based ultrasonic signal denoising

[J]. Journal of Zhejiang University: Engineering Science, 2007, 41 (9): 1557- 1560

[本文引用: 1]

覃柏英, 林贤坤, 张令弥, 等

基于整数编码遗传算法的传感器优化配置研究

[J]. 振动与冲击, 2011, 30 (2): 252- 257

DOI:10.3969/j.issn.1000-3835.2011.02.051      [本文引用: 1]

QIN Bo-ying, LIN Xian-kun, ZHANG Ling-mi, et al

Research on optimal sensor placement based on integer-coded genetic algorithm

[J]. Journal of Vibration and Shock, 2011, 30 (2): 252- 257

DOI:10.3969/j.issn.1000-3835.2011.02.051      [本文引用: 1]

/

〈 〉