混合元胞自动机法(hybrid cellular automaton method,HCAM)[9]是由Tovar耦合了CA法和有限元法(FEM)提出的拓扑优化仿生设计方法,这是无梯度优化算法,计算过程中无需进行敏度分析,解决了CA法没有解决场状态的全局分析问题. HCAM采用FEM来评价场状态(应变能),用FEM计算应变能,作为CA的状态信息,该方法简单易懂、收敛性好、计算效率高、减少了数值不稳定性,可以用于多目标问题的求解,为有效进行结构的拓扑优化设计提供新的分析思路和技术手段[10-11]. 近年来,Tovar等结合能量吸收控制法[12]、谐波振动载荷法[13],将HCAM应用在了车辆防撞器的优化设计、能量收集器外壳和多材料防爆装甲板等的优化设计上[14]. 郭连水等[15]针对大变形非线性结构拓扑优化问题,提出基于HCAM的多空间域连续体结构拓扑优化方法,将基于应变、多域的拓扑优化算法引入HCAM中,进行大变形情况下的车辆防撞性研究[16]. 此外,高云凯等[17]采用HCAM对车辆的保险杠横梁和车身机构进行优化设计. Da等[18]开展极端材料属性情况下的拓扑优化研究.
本文以数值传热学相关理论为基础,采用HCAM对温度−结构场耦合结构的连续体开展无梯度热拓扑设计研究,避免在设计过程中目标函数敏度信息的计算,减少数值的不稳定性;使用该方法对典型算例进行对比分析和优化计算,获得更好的结构构形. 使用HCAM对不同工况下的主轴结构算例进行热拓扑设计,获得更优的主轴热态特性,为减少主轴热致变形、提高机床加工精度提供参考.
1. 不规则元胞的HCAM模型
1.1. 基于不规元胞的HCAM结构优化模型
目前,HCAM都是基于规则的结构元胞,其中最常见的选择是矩形元胞[19]. 在许多情况下,矩形元胞不可能均匀地覆盖设计区域,在实际工程中分析和设计需要使用不规则的元胞来处理复杂的几何图形,在重点关注区域需要对元胞进行局部细化处理. 使用不规则元胞(如边长自适应变化的三角形元胞)来替代HCAM传统的矩形规则元胞,以更好、更灵活地拟合复杂的几何形状,使得求解拓扑构形时能够获得更优的解决方案. 引入局部网格细化的思想在拟合复杂模型的时候,在应力集中或应变急剧变化的区域进行局部元胞细化,从而不需要对整个结构都使用细元胞,以避免元胞数量过多而导致元胞单元与有限元网格之间映射的难度,加快计算速度,增加结果的真实性.
对于离散位置i和离散时间t,HCAM模型的元胞状态集合可以表示为
式中:J为元胞状态的个数,
每个元胞的下一个时刻(t+1)状态由其时刻t状态及其邻域元胞的状态来共同决定. 元胞第J种的状态更新规则可以表示为
式中:
图 1
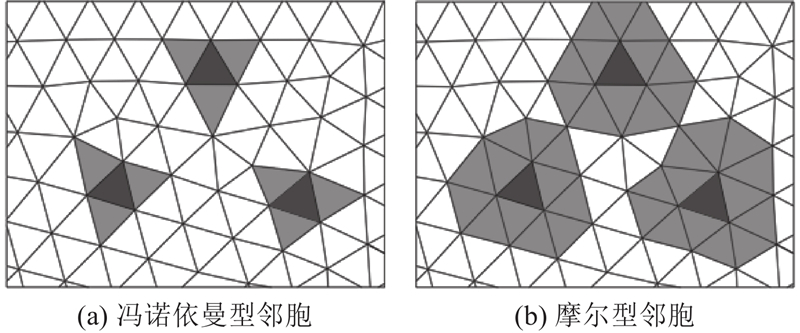
不规则元胞HCAM的邻胞查询规则如下:首先,取出所有元胞及其节点;然后对每个元胞的节点进行比较,若2个元胞有2个相同节点,则定义这2个元胞互为邻胞.
使用HCAM进行拓扑优化迭代的过程中,每个元胞的设计变量
设计变量
式中:
其中,
应变能密度是结构的局部刚性指标,因此使用应变能密度作为场变量,则最优化标准指应变能密度的均匀分布. 根据该标准,CA状态可以定义为
采用HCAM进行结构拓扑优化设计,
式中:
式(7)中有下限
元胞的状态、结构整体的应变能、
式中:Uj为与元胞单元i相邻的邻胞单元j的应变能密度;A为CA中平均每个元胞单元的面积;Ai为元胞单元i的面积;Aj为与元胞单元i相邻的邻胞单元j的面积.
为了扩大HCAM优化模型的适用范围,加快拓扑优化设计的结果收敛,以适应定载荷和变载荷的结构拓扑优化,计算拓扑优化过程中的应变能密度目标值:
式中:aif为权系数,V0为初始结构的体积,Ut为迭代到t次时结构的总应变能.
1.2. 收敛准则
收敛标准由不断更新的设计变量所用的设计规则类型来决定. 将结构质量
式中:M(t)为迭代到t次时结构的质量,ρ为实体材料密度.
当
为了避免收敛过快,收敛准则使用连续2次迭代的平均变化来确定:
式中:
1.3. 局部控制规则
设计域中的材料分布由局部控制规则决定,它寻求的是状态场变量平均值与状态场变量设定值的差值减小到最小. 采用反向控制策略,设计变量的变化用分段常数函数表示:
式中:
为了避免数值计算中的不稳定性,每次迭代过程中设计变量的变化不得超过最大变化量.
2. 基于不规则元胞的HCAM算例拓扑优化设计
为了验证基于HCAM的三角形不规则元胞拓扑优化算法的有效性和普适性,通过不同的图形形状和工况算例来进行拓扑优化设计.
2.1. C型结构拓扑优化设计
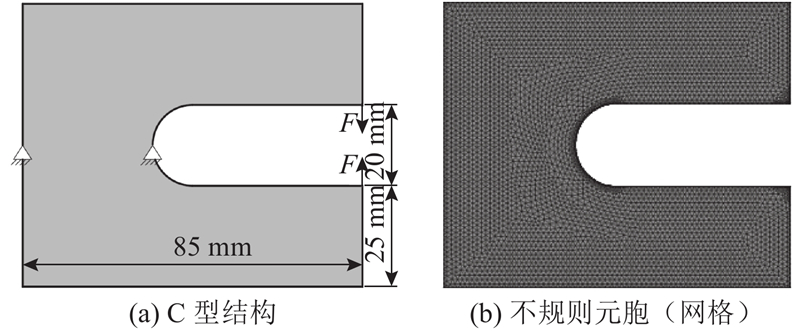
如图2(a)所示的C型结构,基本结构是C型结构的平面板,材料的弹性模量E0=200 GPa、泊松比μ=0.3、密度ρ=7 850 kg/m3. 约束和载荷如图2(a)所示,在两节点处施加固定约束,并在右侧上、下两角节点处施加方向相反、大小为1 000 N的集中力F. 在该案例研究过程中,采用三角形单元作为混合元胞自动机元胞形状,邻胞选择冯诺依曼型;有限元法计算时选择了PLANE183单元(6节点三角形单元),由于右边上、下两角处施加了载荷以及内圆区域会出现应力集中或应变急剧变化,对这三个区域进行局部细化,采用不规则元胞(网格)划分结构后有8 187个三角形元胞(网格),元胞单元尺寸与有限网格单元尺寸保持一致,以便相互映射,结果如图2(b)所示. 初始变量
图 2
图 2 C型结构及其不规则元胞(网格)划分
Fig.2 C-shaped structure and its irregular cells(elements)division result
为了便于观察拓扑优化过程中的构形变化趋势,结合分段函数设置,定义了5种不同弹性模量的单元材料属性以作区分,即
图 3
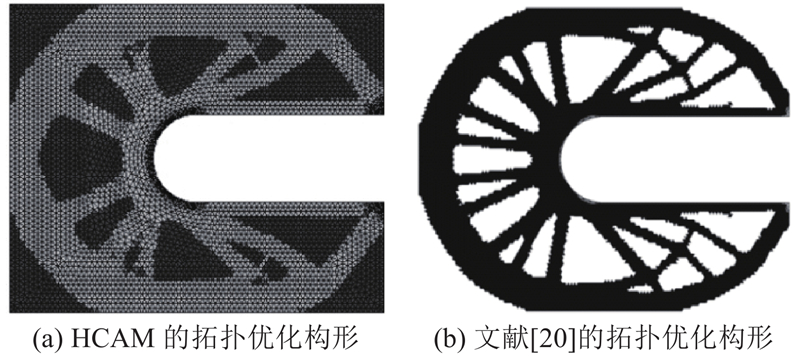
图 3 不同优化算法的C型结构优化结果对比
Fig.3 Results comparison of different optimization algorithms for C-shaped structure
2.2. 半圆环型结构拓扑优化设计
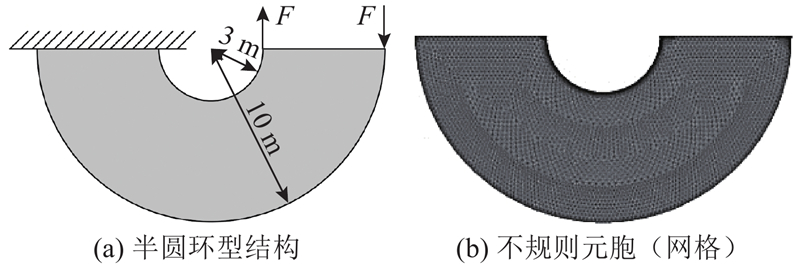
如图4(a)所示的半圆环结构,基本结构是半圆环结构的平面板,大圆半径R=10 m,小圆半径r=3 m,半圆环板的厚度为0.6 m. 材料的弹性模量E0=1 000 Pa、泊松比μ=0.25、密度ρ=7 850 kg/m3. 约束和载荷如图4(a)所示,左侧圆环直线处加固定约束,右侧圆环直线的两端节点上分别施加方向相反、大小为1 N的集中力F,邻胞选择冯诺依曼型. 有限元法计算时,选择PLANE183单元,采用不规则元胞(网格)划分结构后有7 243个三角形元胞(网格),元胞尺寸与有限单元尺寸保持一致,对加载力的两角和内圆弧区域进行局部细化,结果如图4(b)所示. 初始变量
图 4
图 4 半圆环型结构及其不规则元胞(网格)划分
Fig.4 Half-ring structure and its irregular cells(elements)division result
图 5
图 5 不同优化算法的半圆环型结构优化结果对比
Fig.5 Results comparison of different optimization algorithms for half-ring structure
3. 基于不规则元胞HCAM的结构温度−结构场耦合拓扑优化
3.1. 结构温度−结构场耦合模型
结构温度场的分布不均会引起结构的热应力,热应力的产生与温度变化和约束有关,在温度变化下,当结构发生自由变形时,不产生热应力;当自由变形受约束时,会产生热应力. 同一物体内部若温度分布不均匀,虽然物体不受外界约束,但由于各处温度不同,每部分受到不同温度相邻部分的约束不能自由伸缩,会产生热应力. 若温升过高,则产生的热应力将超过材料的屈服极限[21],因此温度−结构场耦合问题是进行结构分析与优化时需要考虑的重要因素. 考虑在热载荷影响下,通过热拓扑结构优化使得结构的应变能密度分布达到一个较优效果. 当获得了相应的应变和热应力结果时,可以基于HCAM通过寻找设置的应变能密度目标开展温度−结构场耦合情况下的结构拓扑优化.
基于能量守恒定律建立的对于结构模拟件中无内热源的稳定传热,热平衡方程式为
式中:x、y、z为空间坐标,θ为温度.
热问题的基本有限元方程可以由热平衡方程推导求得:
式中:
根据牛顿冷却定律和能量守恒定律,边界条件为
式中:n为结构表面法线方向(向物体外为正),λ为结构模拟件的热导率,
通过线性热应力理论[21]可知,微元体的总应变由2部分组成:一部分是由应力引起的,另一部分是由温度变化引起的. 用热应力及温差表示应变的平面应力下的广义虎克定律表示为
式中:
引进符号:
则式(18)可以化简为另一种形式的物理方程式:
将式(20)的三式相加,可以改写成
式(21)表明,线应变之和与3倍温度应变之差正比于正应力之和. 将式(21)代入式(20),可得
式中:
可得由应变分量及温度分量表示的热应力分量公式:
对于切应力而言(按切应力互等定律),
对于连续体结构空间的温度−结构场耦合分析问题而言,计算模型中有15个未知函数、6个应力分量、6个应变分量、3个位移分量,这15个未知函数应满足15个基本方程式,即3个平衡方程式、6个几何方程式、6个物理方程式. 将式(18)~(24)联立,当已知温度场分布时,可以求解热位移、热应力与热应变. 这是本文的温度-结构场耦合分析理论依据.
当采用HCAM进行温度−结构场耦合优化时,将设计空间内的材料分布情况通过CA控制局部变化规则得出,同时利用有限元软件获得因材料密度变化而引起的结果. 在进行有限元计算时,采用顺序耦合分析方法,先进行温度场分析求得结构中的温度分布,再进行结构场分析,将得到的温度场结果作为体载荷加到结构场分析中,求解该情况下的结构热应力分布,通过HCAM来获得热拓扑设计的优化构形.
3.2. 结构温度−结构场耦拓扑优化算例
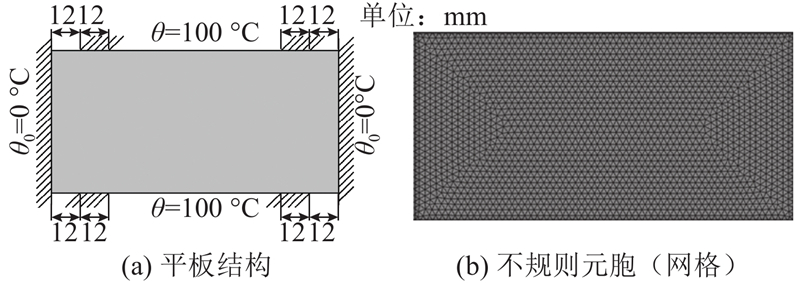
采用如图6(a)所示的平板结构作为温度−结构场耦合拓扑优化测试用例. 该结构为左右两端和内部有固定约束的平面结构,基本尺寸为
图 6
图 6 温度-结构场耦合的平板结构及不规则元胞(网格)划分
Fig.6 Flat structure under temperature-structure field coupling and its irregular cells(elements)division results
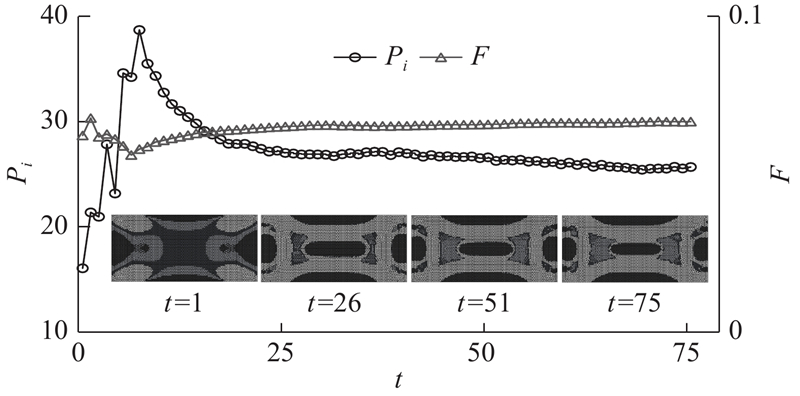
最终求解该结果的迭代次数为75次,迭代过程中得到的部分拓扑优化构形如图7所示. 图中,黑色区域代表的是须去除区域(热传导率为0),白色区域代表须保留区域(热传导率为λ0),其他颜色介于两者之间.
图 7
图 7 HCAM得到的平板结构拓扑优化构形图
Fig.7 Selected intermediate and final topologies of flat structure based on HCAM
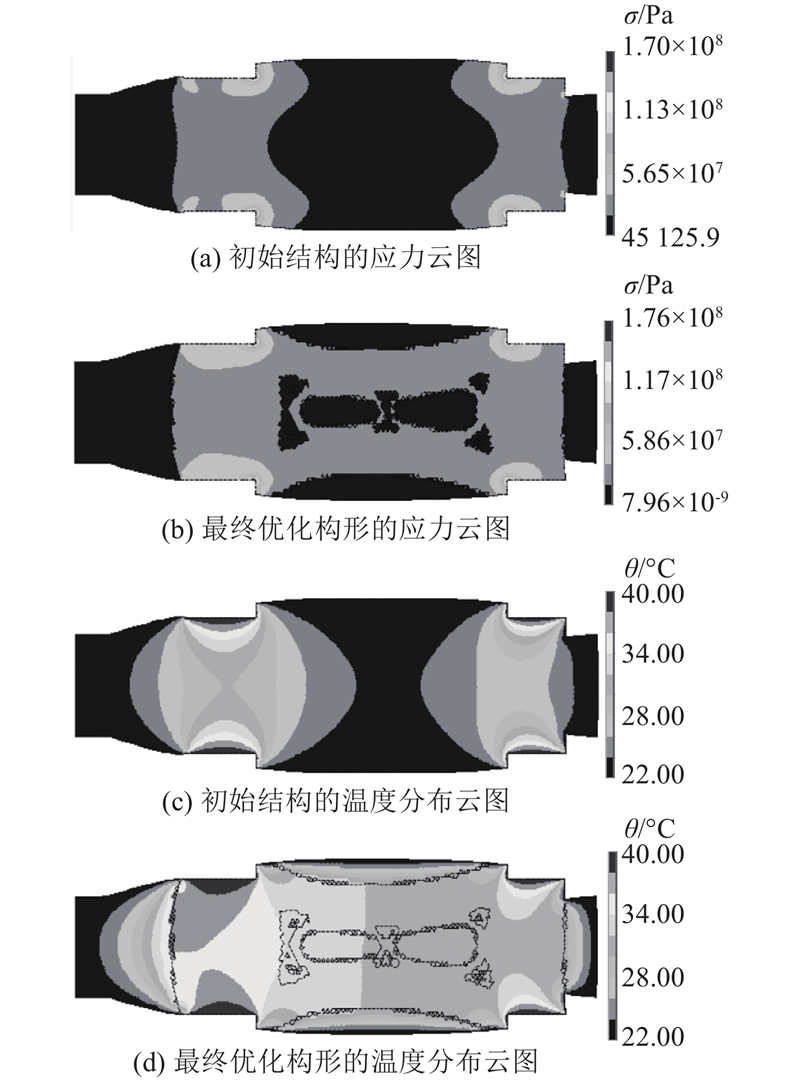
如图8所示为优化前、后的结果对比. 从图8(a)、(b)可见,初始结构和最终优化构形的最大应力都出现在两端和中间约束处,黑色区域处的应力是最低的,这个黑色的区域与拓扑优化结果中得到的须去除区域保持一致. 初始结构的最大应力
图 8
图 8 平板结构优化前、后的结果比较
Fig.8 Before and after optimization results comparison of flat structure
图 9
4. 基于不规则元胞HCAM的主轴温度−结构场耦合拓扑优化
4.1. 温度载荷作用下的主轴测试用例拓扑优化
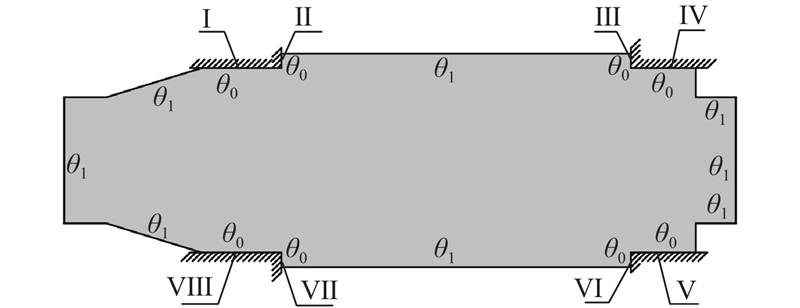
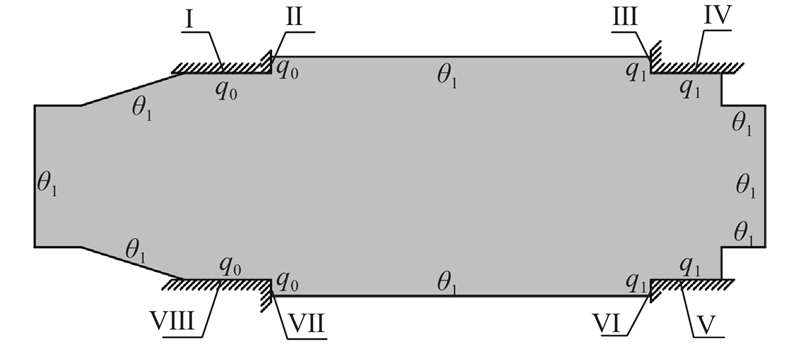
参考文献[5]的主轴系统结构,采用如图10所示的温度载荷作用下的主轴拓扑优化测试用例,材料的E=100 GPa,μ=0.25,ρ=7 850 kg/m3,a=1.0×10−5,λ0=40 W/(m·K). 该结构Ⅰ−Ⅷ为安装轴承处,因此在Ⅰ、Ⅳ、Ⅴ和Ⅷ处设置径向固定约束,在Ⅱ、Ⅲ、Ⅵ和Ⅶ设置轴向固定约束,并且在Ⅰ−Ⅷ处施加θ0=40 °C的温度载荷,主轴其余与环境接触的部位为θ1=22 °C,求重量最轻的拓扑构形. 将图10所示的温度载荷作用下的主轴拓扑优化测试用例划分为8 792个不规则三角形元胞,元胞尺寸与有限元单元尺寸相同. 在该案例计算过程中,设置了5种不同热传导率的单元材料,即λ0、0.75λ0、0.5λ0、0.25λ0、0. 结构邻胞选择冯诺依曼型,有限元法计算时选择Plane55单元,并且在Ⅰ和Ⅱ、Ⅲ和Ⅳ、Ⅴ和Ⅵ、Ⅶ和Ⅷ相交处(将产生应力集中处)进行元胞(网格)局部细化处理,将结构划分为8 792个三角形元胞(网格),元胞尺寸与有限单元尺寸保持一致,划分结果如图11所示.
图 10
图 11
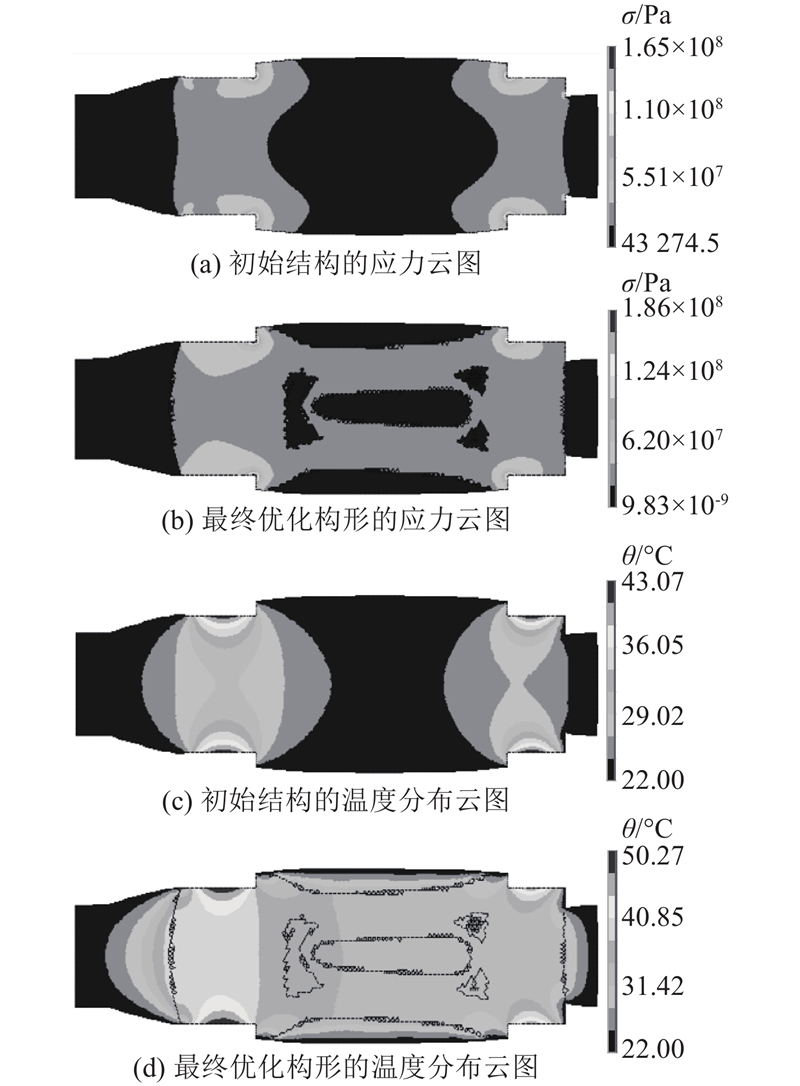
最终求解该结果的迭代次数为23次,迭代过程中得到的部分拓扑优化构形如图12所示. 如图13所示为优化前、后的结果对比. 从图13(a)、(b)可见,初始结构和最终优化构形的最大应力都出现在两端和中间约束处,黑色区域处的应力是最低的,这个黑色的区域与拓扑优化结果中得到的须去除区域保持一致. 此外,初始结构的
图 12
图 12 HCAM得到的主轴测试用例拓扑优化构形图
Fig.12 Selected intermediate and final topologies of spindle test case based on HCAM
图 13
图 13 主轴测试用例优化前、后的结果比较
Fig.13 Before and after optimization results comparison of spindle test case
图 14
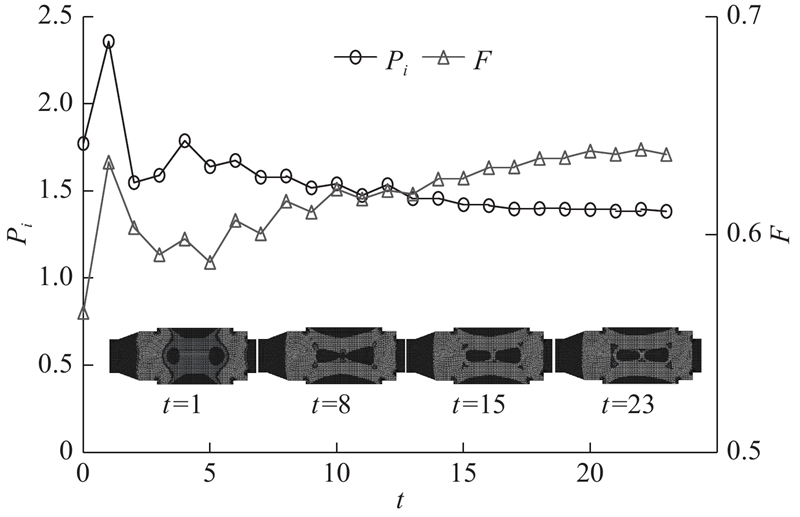
图 14 HCAM的性能指标和质量比历程曲线图
Fig.14 Performance index and quality ratio history curve of HCAM
4.2. 热流载荷作用下的主轴测试用例拓扑优化
图 15
最终求解该结果的迭代次数为36次,迭代过程中得到的部分拓扑优化构形如图16所示. 如图17所示为优化前、后的结果对比. 从图17(a)、(b)可见,初始结构和最终优化构形的最大应力都出现在两端和中间约束处. 图中,黑色的区域与拓扑优化结果中得到的须去除区域保持一致. 初始结构的
图 16
图 16 HCAM得到的主轴测试用例拓扑优化构形图
Fig.16 Selected intermediate and final topologies of spindle test case based on HCAM
图 17
图 17 主轴测试用例优化前、后的结果比较
Fig.17 Before and after optimization results comparison of spindle test case
图 18
图 18 HCAM的性能指标和质量比历程曲线图
Fig.18 Performance index and quality ratio history curve of HCAM
5. 结 语
本文提出基于不规则元胞的HCAM主轴耦合场热拓扑优化设计方法. 该方法以数值传热学相关理论为基础,将边长自适应变化的三角形元胞来替代HCAM传统的矩形规则元胞,更好、更灵活地适应了复杂的几何形状,避免了矩形元胞不能均匀地覆盖设计区域的问题,使得求解拓扑构形时能够获得更优的解决方案. 该方法引入局部网格细化的思想,可以实现在应力集中或应变急剧变化的区域进行元胞细化,不需要对整个结构都使用同一尺寸的规则元胞,从而有效地避免了元胞数量过多、导致元胞单元与有限元网格之间映射的难度. 本文利用不规则元胞的HCAM,对主轴结构进行温度−结构场耦合热拓扑优化设计. 通过温度载荷和热流载荷的算例发现,使用该方法可以有效地去除主轴结构多余材料,改善热态特性.
参考文献
Thermal issues in machine tools
[J].DOI:10.1016/j.cirp.2012.05.008 [本文引用: 1]
Thermo-mechanical behavior analysis of motorized spindle based on a coupled model
[J].
Machine tool spindle units
[J].DOI:10.1016/j.cirp.2010.05.002 [本文引用: 1]
机床主轴热设计研究综述
[J].
Review on thermal design of machine tools’ spindle
[J].
精密数控机床主轴系统多物理场耦合热态特性
[J].
Multi-field coupling thermal characteristics analysis for spindle system of the precision CNC machine tool
[J].
Novel local rules of cellular automata applied to topology and size optimization
[J].DOI:10.1080/0305215X.2011.561843 [本文引用: 1]
Application of cellular automata to size and topology optimization of truss structures
[J].DOI:10.1016/j.scient.2012.04.009 [本文引用: 1]
Influence of the topology of a cellular automaton on its dynamical properties
[J].DOI:10.1016/j.cnsns.2012.08.018 [本文引用: 1]
Optimality conditions of the hybrid cellular automata for structural optimization
[J].
Topology optimization using a hybrid cellular automaton method with local control rules
[J].DOI:10.1115/1.2336251 [本文引用: 1]
Design of crashworthy structures with controlled energy absorption in the hybrid cellular automaton framework
[J].
Topology optimization of piezoelectric energy harvesting skin using hybrid cellular automata
[J].
Two-material optimization of plate armor for blast mitigation using hybrid cellular automata
[J].DOI:10.1080/0305215X.2011.624182 [本文引用: 1]
一种大变形多空间域连续体结构拓扑优化方法
[J].
Method of multi-domain topology optimization for continuum structures
[J].
Strain-based topology optimization for crashworthiness using hybrid cellular automata
[J].
基于混合元胞自动机的铝合金保险杠横梁设计
[J].
Design of an aluminum bumper beam based on hybrid cellular automata
[J].
Design of materials using hybrid cellular automata
[J].DOI:10.1007/s00158-017-1652-1 [本文引用: 1]
Research on thermal topology design method of spindle based on HCAM
[J].DOI:10.1088/1757-899X/281/1/012048 [本文引用: 1]
GOTICA - generation of optimal topologies by irregular cellular automata
[J].DOI:10.1007/s00158-016-1614-z [本文引用: 2]