随着航空航天[1-2]、机器人[3]、医疗器械、交通运输等领域的快速发展,其中的关键部件之一谐波减速器逐渐成为近年来的研究重点,人们也对其提出了更严苛的要求. 区别于传统刚性构件的传动方式,谐波传动通过构建可控制弹性变形来实现机械运动的传递,具有结构紧凑、传动平稳、效率高、轻量化等优点. 由柔轮、刚轮、波发生器三大部件组成的谐波减速器最主要的失效形式是柔轮的疲劳断裂[4],因此,柔轮的应力与变形规律是当前研究重点. 为减小啮合应力,增加柔轮疲劳寿命,许多学者针对齿廓形状参数[5-6]、结构参数[7-8]等因素进行了大量研究. 王家序等[9]提出的三维双圆弧空间齿廓,提高了啮合性能. 杨勇等[10]针对双圆弧谐波齿廓传动,提出一种增大“双共轭”啮合区间的求解方法,优化了齿廓参数,提高了扭转刚度及传动精度. 随着计算机技术的快速提高,有限元法逐渐成为研究谐波传动应力变化的主要手段. 李奇[11]采用有限元法,分析柔轮结构不同参数,发现柔轮径向变形对柔轮应力以及疲劳寿命影响最大,壁厚和长径比次之. 张雷等[12]基于有限元法与响应面法,综合分析了柔轮圆角、凸轮结构等参数对柔轮刚度和内壁、齿圈等的应力影响规律,但是未考虑齿形的影响. 然而,在实际加工过程中提高齿廓的加工制造精度是减小啮合应力、提高啮合性能的最主要手段. 刚轮与柔轮的齿厚偏差、凸轮长短轴偏差是能够通过检测来量化的4个重要参数. 但是,如何通过优化上述可检验项目上、下偏差取值来控制柔轮的应力,进行实验探究及定量分析,目前仍然没有文献涉及.
本文以无公切线式双圆弧齿廓为研究对象,考虑引起谐波传动齿廓变化的三大重要构件制造误差,包括刚轮与柔轮的齿厚误差和凸轮的长短轴加工误差,通过响应面法与有限元法揭示谐波齿轮制造误差对柔轮应力分布情况的影响规律,以期得到生产制造中对柔轮应力影响最小的误差范围,减少因高加工精度带来的高成本.
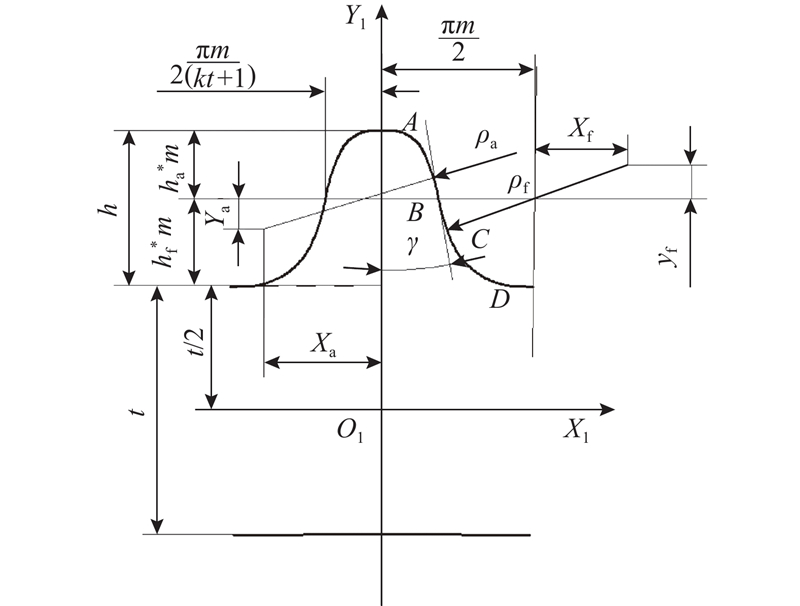
1. 双圆弧谐波传动齿廓设计
图 1
图 1 双圆弧齿廓坐标系
Fig.1 Tooth profile of flexspline with double-circular-arc tooth profile
表 1 双圆弧齿廓参数
Tab.1
| 符号 | 意义 | 符号 | 意义 | |
| | 齿顶高系数 | | 公切线倾角 | |
| | 齿根高系数 | | 齿根壁厚 | |
| | 全齿高 | | 凸齿圆心移距量 | |
| | 凸圆弧齿廓半径 | | 凸齿圆心偏移量 | |
| | 凹圆弧齿廓半径 | | 凹齿圆心移距量 | |
| | 凹齿圆心偏移量 | m | 柔轮模数 | |
| kt | 齿厚比 | − | − |
根据图1,以从齿顶A处起的齿廓弧长u为参数,r为右侧齿廓的矢径,
1)在AB段上:
式中:
2)在BC段上:
式中:
首先建立啮合基本方程并采用包络法设计刚轮的理论共轭齿廓. 采用数值离散思想,将各段的弧长参数u离散成s个点,再将对应齿廓段点的r、n代入啮合基本方程,即可求得该点刚柔轮共轭转角集,最后通过坐标变换求得与柔轮齿廓共轭的刚轮理论齿廓.
2. 谐波齿轮制造误差分析
2.1. 齿厚偏差
按照谐波减速器的建构组成,将制造误差分为柔轮、刚轮和凸轮制造误差. 柔轮、刚轮的制造误差主要以传动侧隙的大小影响谐波齿轮传动工作性能,为本实验主要研究对象. 侧隙较大会产生齿间冲击,影响齿轮传动的平稳性. 一般传递运动的精密谐波齿轮传动要求其最小侧隙为零. 侧隙是在谐波齿轮传动中柔轮与刚轮啮合处的间隙,其大小以圆周侧隙jt表示,设K1(XK1,YK1)为柔轮齿廓上某点的坐标,以rK 为半径作圆弧与相邻刚轮齿廓相交,可得到对应刚轮齿廓上的交点K2(XK2,YK2),则有
当谐波齿轮承受负载时,柔轮产生弹性扭转变形,并使轮齿产生附加的切向位移,如果侧隙过小,将会引起变形干涉,故将柔轮因弹性变形而引起的侧隙减小量je作为分析因素之一,计算公式为
式中:T为作用的扭矩,b为柔轮齿宽;d1为柔轮分度圆直径,δ为柔轮壁厚,G为柔轮剪切模量.
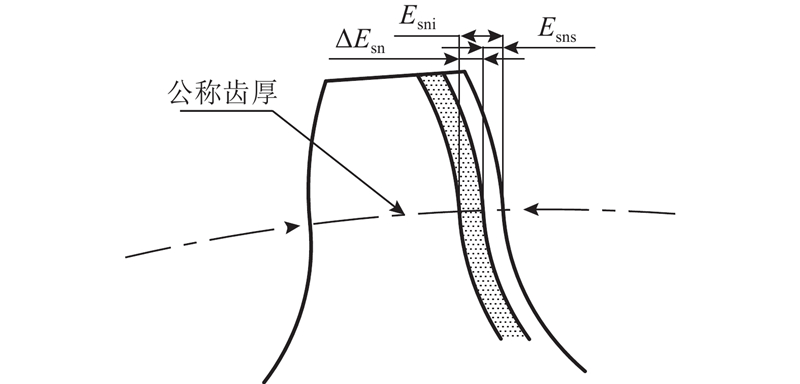
传动侧隙的大小取决于齿厚偏差ΔEsn,其指分度圆柱面上法向齿厚实际值与公称值之差. Esns为齿厚上偏差,Esni为齿厚下偏差. 如图2所示为齿厚偏差示意图. 在工程实际中一般采用测量跨距值(M值)的方式来度量齿厚偏差. 对于圆弧齿轮,量柱与齿面接触为一直线,测量方便. 该方法计算简便、测量准确、数值稳定,且不需要测量基准面,消除了齿顶圆误差、孔径误差和齿圈径向跳动的影响,适用于谐波齿轮的测量.
图 2
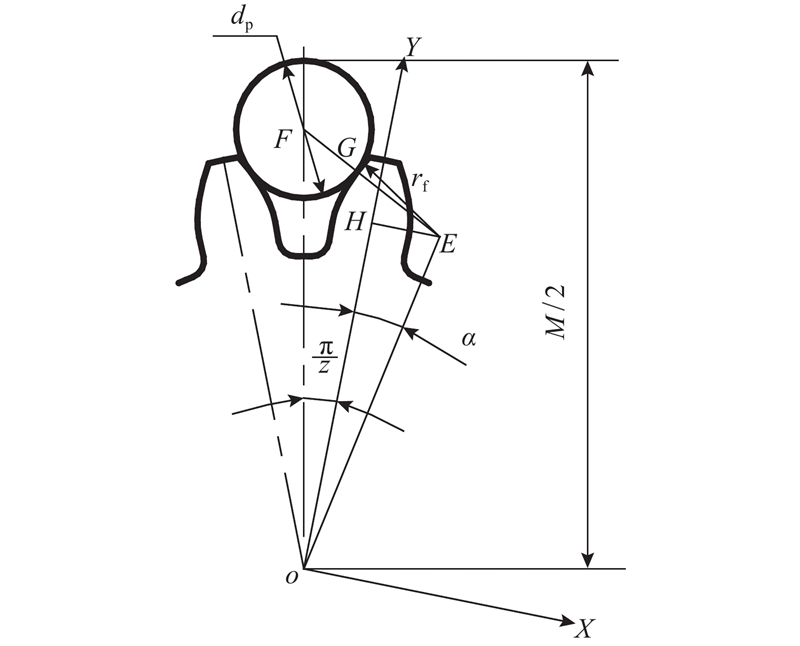
2.1.1. 柔轮理论M值的计算原理
柔轮为外啮合齿轮,设点E为柔轮齿凸齿廓的圆心,其坐标为E(xE,yE),点F为量柱的圆心,点H为点E在Y轴上的投影. 量柱与凸齿廓接触相切于点G,显然点E、F、G在同一条直线上. 如图3所示为柔轮齿廓理论M值计算原理图,图中,z为柔轮齿数,α为柔轮半齿角,dp为量柱直径,dM为测量跨距值时的实际读数(量柱直径与跨距值之和),则有
图 3
图 3 柔轮齿廓理论M值计算原理图
Fig.3 Schematic diagram of theoretical M-value for tooth profile of flexspline
由三角形余弦定理可知:
由式(7) ~ (10)可得柔轮齿廓的理论M值.
2.1.2. 刚轮理论M值的计算原理
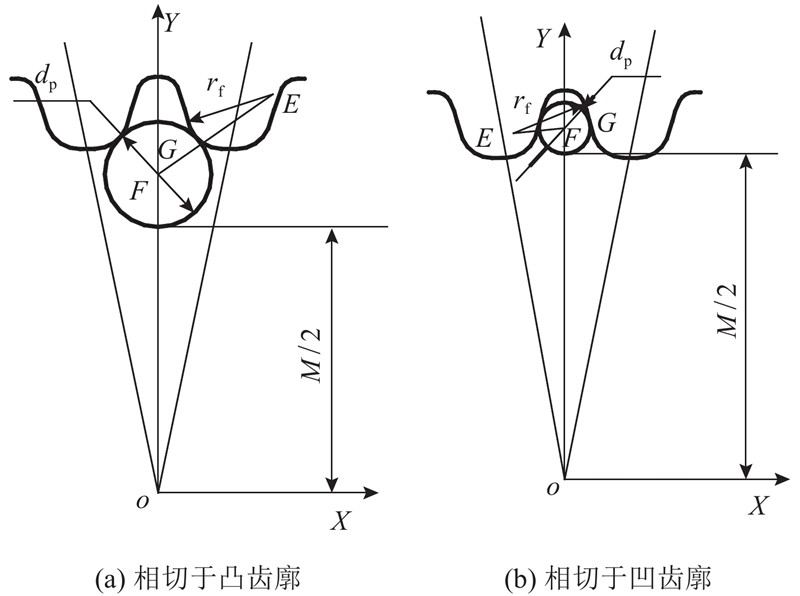
刚轮为内啮合齿轮,选择不同直径大小的量柱,量柱会与刚轮不同的齿廓段相切.
1)相切于凸齿廓的刚轮理论M值的计算.
当选择较大直径的量柱时,量柱与刚轮凸齿廓相切,如图4(a)所示为相切于凸齿廓的刚轮齿廓理论跨距值计算原理图,则有
图 4
图 4 刚轮齿廓理论M值计算原理图
Fig.4 Schematic diagram of theoretical M-value for tooth profile of circular spline
由式(8)~(11)可求得lOF值,从而得到相切于凸齿廓的刚轮齿廓理论M值.
2)相切于凹齿廓的刚轮理论M值的计算.
选择较小直径的量柱,则会与刚轮相切于凹齿齿廓,如图4(b)所示为相切于凹齿廓的刚轮齿廓理论M值计算原理图,则有
由式(8)、(10)~(12),可得到相切于凹齿廓的刚轮齿廓理论M值. 通过比较理论M值和实际测量M值,即可确定制造精度.
2.2. 凸轮长短轴偏差
波发生器迫使柔轮作弹性波动变形,决定了谐波齿轮传动的运动原始曲线,故波发生器的制造误差对谐波传动的精度影响显著. 凸轮长短轴偏差对标准椭圆凸轮制造误差影响显著,直接影响柔轮径向变形量,改变了柔轮筒体张角大小,进而影响谐波齿轮应力状态,因此将凸轮长短轴偏差作为分析因素之一.
设椭圆波发生器长短轴半径分别为a、b,柔性轴承厚度为t′,波发生器最大径向变形量为w0′,柔轮内径为de,则上述参数存在以下关系:
3. 采用响应面法分析制造误差对柔轮应力变化规律的影响
3.1. 响应面法的外切中心复合设计
响应面分析法(response surface methodology, RSM)通过选取合适的因素水平,设计较少的实验次数并拟合获得因素与响应值之间良好的函数关系,是寻求最优参数的一种解决多因素影响问题的数学统计方法. 中心复合设计(central composite designs, CCDs)因其以最小实验次数提供较多关于实验因素与误差的信息与更好的灵活性等优点,在工程、工业等领域应用颇广. CCDs拟合的二阶响应曲面模型[15]为
式中:y为响应变量,β0为常量,βi、βij、βii为各项系数,xi为各项自变量,ε为误差项. 模型中共有1+2k+k(k−1)/2个参数,由于k≥1,至少有3个参数,即因素至少要有3个水平.
CCDs又分为外切中心复合设计(central composite circumscribed designs,CCC)、嵌套中心复合设计(central composite inscribed designs,CCI)、面心立方设计(central composite face-centred designs,CCF). 有以下关系式:
式中:k为因素个数,η为轴向距离参数,F为析因设计点的数目.
对3种模型的拟合参数比较发现,CCC估计的一致精度最高,模型参数估计最有效且具有可旋转性,故选择采用CCC模型进行本次实验设计.
3.2. 基于外切中心复合设计的多因素多水平实验
为研究谐波减速器各个制造误差对柔轮齿上应力的影响,拟合出各制造误差与柔轮齿上观测点应力的函数关系模型,通过Design Expert响应面法实验设计软件设计多因素多水平实验. 其中,研究因素如下:柔轮M值偏差δ1,刚轮M值偏差δ2,凸轮长半轴偏差δ3,凸轮短半轴偏差δ4,共4个因素,即k=4,通过式(15)得到η=2,F=16.
由于目前没有可查阅的双圆弧柔性齿轮精度等级标准,本实验参考小模数渐开线圆柱齿轮精度及参数表,柔轮采用六级制造精度,刚轮采用七级精度. 综合采集到工厂生产的CSF25-120谐波减速器样机制造误差数据,计算出样机的刚轮与柔轮M值,以及凸轮长短半轴误差取值范围. 如表2所示为最终实验的因素范围与水平. 通过对不同因素水平合理组合设计得到30组实验.
表 2 谐波齿轮制造误差因素水平表
Tab.2
| 水平编码 | δ1/mm | δ2/mm | δ3/mm | δ4/mm |
| −2 | −0.050 | −0.050 | −0.050 | −0.050 |
| −1 | −0.025 | −0.025 | −0.025 | −0.025 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0.025 | 0.025 | 0.025 | 0.025 |
| 2 | 0.050 | 0.050 | 0.050 | 0.050 |
3.3. 谐波齿轮传动响应面模型建立
3.3.1. 谐波齿轮传动有限元分析
由于样机制作成本较高,且有限元法与理论计算结果较为一致[16],目前有限元分析(finite element analysis,FEA)被广泛用于研究谐波齿轮传动的柔轮应力研究.
本次实验建模以哈默纳科(Harmonic Drive,HD)公司的CSF-25-120为实例,传动比i=120,柔轮齿数z1=240,刚轮齿数z2=242,柔轮内壁直径de=61.32 mm. 采用压平设计的标准椭圆凸轮,其理论径向变形量w0'=0.261 mm,计算出刚轮理论M值为63.354 9 mm,柔轮理论M值为64.081 7 mm.
图 5
图 5 谐波齿轮有限元分析(FEA)模型网格划分
Fig.5 Meshing of harmonic gear finite element analysis (FEA) model
表 3 谐波齿轮材料物理性能参数
Tab.3
| 部件 | 材料 | E/GPa | μ | ρ/(kg·m−3) |
| 柔轮 | 30CrMnSiA | 196 | 0.3 | 7 750 |
| 刚轮 | 45 | 210 | 0.269 | 7 850 |
| 波发生器 | 45 | 210 | 0.269 | 7 850 |
为减少工作量并缩短求解时间,对模型作部分结构上的简化. 将波发生器简化为椭圆刚体,去掉柔轮杯底螺栓孔,刚轮只取有齿部分并简化为内圆柱齿圈. 因加载对柔轮齿应力影响很小[16],不考虑加载,设置以下2个分析步骤.
1)在柔轮法兰盘面建立耦合点,对该点加上固定约束,波发生器椭圆分为上、下两半,分别设置上、下位移约束,使波发生器外表面分别与柔轮内壁进行挤压接触,将其撑开.
2)在刚轮外圆表面建立耦合点,并对该点添加位移约束,将刚轮装进柔轮,与柔轮装配,刚轮与柔轮齿廓进行接触.
图 6
3.3.2. 响应面模型的建立
采集有限元仿真实验各组数据,基于响应面思想拟合得到柔轮M值偏差δ1、刚轮M值偏差δ2、凸轮长半轴偏差δ3、凸轮短半轴偏差δ4四因素对于柔轮齿上固定观测点应力σ的响应面模型如下:
对该方程进行回归显著性检验,P值大于F值的概率小于0.001,表明该模型具有统计学意义,显著性表现为显著. 对各因素进行敏感度分析,一次项系数显示各因素的重要程度为δ3>δ2>δ1>δ4,二次项系数显示各因素的重要程度为δ3>δ2>δ4>δ1. 综合分析可知,δ3对该模型的影响程度最大,δ2和δ1次之,δ4的影响程度最小. 即凸轮长半轴偏差对柔轮齿上应力敏感度最大,刚轮M值偏差、柔轮M值偏差次之,凸轮短半轴偏差敏感度最小. 因此在实际生产过程中,为达到产品高性能及低成本的目标,需优先保证凸轮长半轴加工精度,再保证其他因素的精度.
为探究各因素对柔轮应力的具体影响规律,根据得到的数学模型,对上述4个因素分别进行定量分析.
3.4. 基于响应面模型的单因素对柔轮应力影响
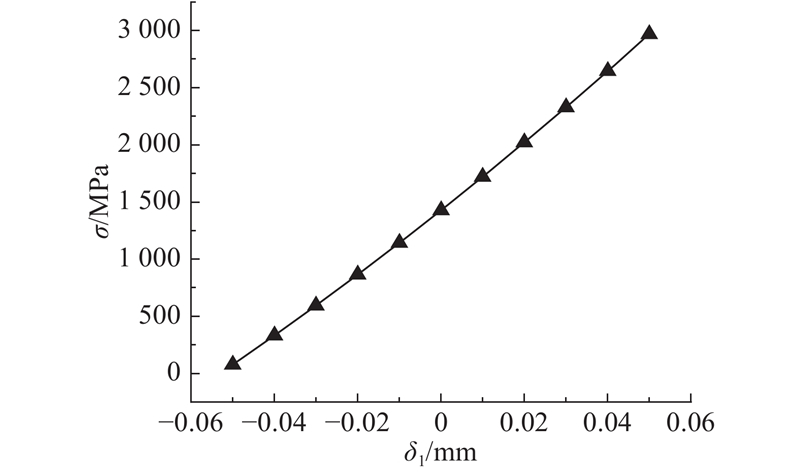
3.4.1. 柔轮M值偏差对柔轮齿上应力的影响
图 7
图 7 柔轮M值偏差对柔轮齿上观测点应力影响曲线
Fig.7 Effect of M-value deviation of flexspline on stress of flexspline tooth observation point
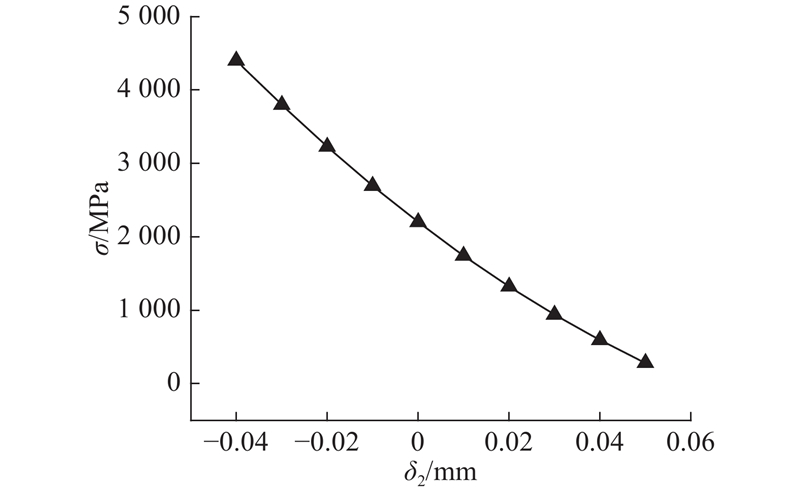
3.4.2. 刚轮M值偏差对柔轮齿上应力的影响
图 8
图 8 刚轮M值偏差对柔轮齿上观测点应力影响曲线
Fig.8 Effect of M-value deviation of circular spline on stress of flexspline tooth observation point
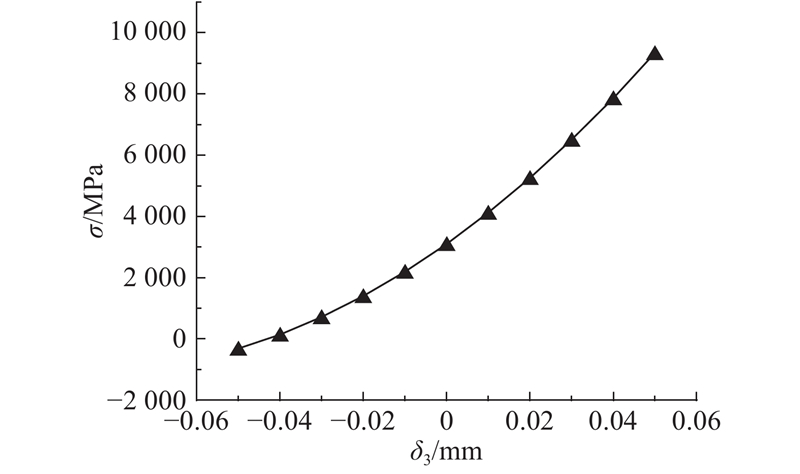
3.4.3. 凸轮长半轴偏差与短半轴偏差对柔轮齿上应力的影响
图 9
图 9 凸轮长半轴偏差对柔轮齿上观测点应力影响曲线
Fig.9 Effect of cam long half axis deviation on stress of flexspline tooth observation point
图 10
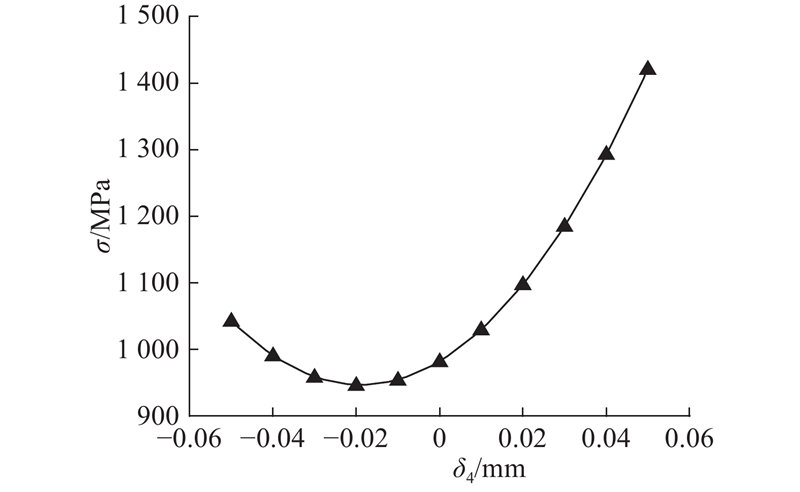
图 10 凸轮短半轴偏差对柔轮齿上观测点应力影响曲线
Fig.10 Effect of cam short half axis deviation on stress of flexspline tooth observation point
图 11
图 11 柔轮与刚轮M值偏差对柔轮齿上观测点应力的响应面3D图
Fig.11 Response surface of M-value deviation of flexspline and circular spline on stress of flexspline tooth observation point
图 12
图 12 柔轮M值偏差与凸轮长半轴偏差偏差对柔轮齿上观测点应力的响应面3D图
Fig.12 Response surface of M-value deviation of flexspline and cam long half axis deviation on stress of flexspline tooth observation point
图 13
图 13 刚轮M值偏差与凸轮长半轴偏差偏差对柔轮齿上观测点应力的响应面3D图
Fig.13 Response surface of M-value deviation of circular spline and cam long half axis deviation on stress of flexspline tooth observation point
3.5. 不同参数制造误差补偿方案设计
柔轮的传动精度决定着谐波减速器的传动精度. 在谐波减速器各部件的生产加工过程中,无可避免会出现刚轮、柔轮齿廓加工误差,从而引起柔轮齿上应力集中,影响啮合性能. 一般来说,刚轮与柔轮齿加工难度及生产成本较高,而凸轮形状规则,加工难度和生产成本较低. 故在刚轮、柔轮已完成生产加工后,可通过调整凸轮来控制刚轮与柔轮齿廓加工误差导致的应力变化. 现根据实际生产中四种不同情形,设计出以下4种应力补偿方案. 如图14所示为凸轮的4种调整方案曲线. 图中,Δ1、Δ2、Δ3、Δ4为4种方案凸轮长半轴的调整量.
图 14
图 14 4种方案的凸轮长半轴调整曲线
Fig.14 Adjustment curves of cam long half axis by four kinds of solutions
1)方案一:当柔轮M值、刚轮M值为负偏差,可采用减小凸轮长半轴的方式以减小柔轮应力. 例如当柔轮M值偏差δ1=−0.02mm,刚轮M值偏差δ2=−0.02 mm,柔轮齿上应力σ与凸轮长半轴调整量Δ1关系曲线如图14(a)所示.
2)方案二:当柔轮M值偏差、刚轮M值偏差为正偏差,可增大凸轮长半轴以改善啮合不足. 例如当柔轮M值偏差δ1=0.02 mm,刚轮M值偏差δ2=0.05 mm,柔轮齿上应力σ与凸轮长半轴调整量Δ2关系曲线如图14(b)所示.
3)方案三:当柔轮M值偏差为负偏差,刚轮M值偏差为正偏差,可采取增大凸轮长半轴的方式来改善啮合不足。例如柔轮M值偏差δ1=−0.03 mm,刚轮M值偏差δ2=0.03 mm,柔轮齿上应力σ与凸轮长半轴调整量Δ3关系曲线如图14(c)所示。
4)方案四:当柔轮M值偏差为正偏差,刚轮M值偏差为负偏差,可采取减小凸轮长半轴的方式以减小柔轮应力。例如当柔轮M值偏差δ1=0.02 mm,刚轮M值偏差δ2=−0.02 mm,柔轮齿上观测点应力σ与凸轮长半轴调整量Δ4关系曲线如图14(d)所示。
4. 结 论
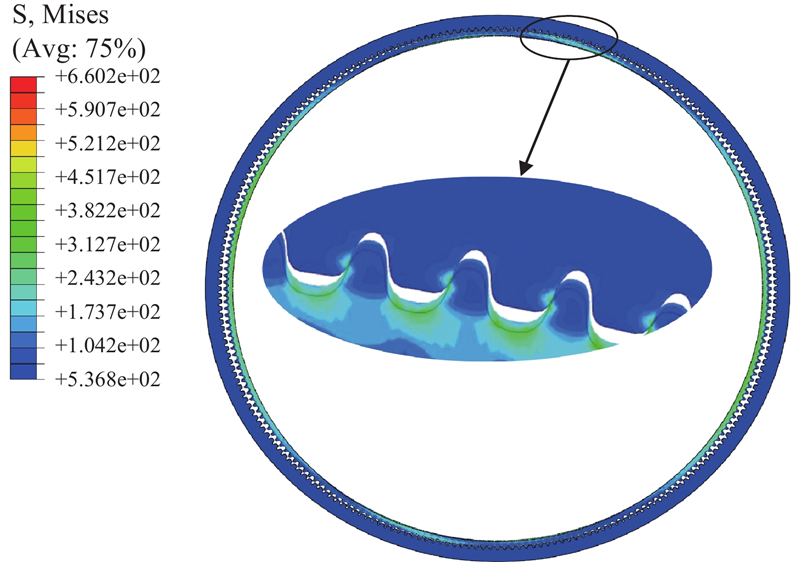
(1)在刚轮与凸轮的共同作用下,柔轮上最大应力出现在柔轮齿面啮入区位置处.
(2)凸轮长半轴偏差对柔轮应力影响最大,柔轮M值偏差、刚轮M值偏差次之,凸轮短半轴偏差最小. 若凸轮长半轴或柔轮M值增大,柔轮齿上应力随之增大;若刚轮M值增大,柔轮齿上应力减小;柔轮齿上应力随凸轮短半轴先减小后增大,但变化很小.
(3)在谐波减速器的加工制造过程中,当刚轮与柔轮出现齿廓偏差时,可通过控制凸轮长半轴偏差来使谐波减速器轮齿啮合情况不受较大影响,改善啮合情况,提高精度保持性,降低生产成本和废品率.
参考文献
空间高精度谐波减速器的应用及其发展趋势
[J].
Application and development trends of the space harmonic reducer with high precision
[J].
谐波减速器测试技术研究现状及展望
[J].
Research present status and outlook of harmonic reducer testing technology
[J].
变刚度关节驱动器动力学特性的分析与研究
[J].
Analysis and study on dynamical characteristics of variable stiffness joint actuator
[J].
谐波减速器柔轮疲劳分析
[J].
Fatigue analysis of the harmonic reducer flexspline
[J].
Statistical analysis of the influence of tooth geometry in the performance of a harmonic drive
[J].DOI:10.1007/s40430-014-0197-0 [本文引用: 1]
基于正交试验和有限元分析的谐波传动柔轮杯体结构优化
[J].
Structural optimization of the flexspline cup in harmonic drives based on orthogonal test and finite element analysis
[J].
杯形柔轮谐波传动三维双圆弧齿廓设计
[J].
Three dimensional profile design of cup harmonic drive with double-circular-arc common-tangent tooth profile
[J].
双圆弧谐波齿轮传动柔轮齿廓参数的优化设计
[J].
Optimization design for flexspline tooth profile parameters of double-circular-arc harmonic drives
[J].
谐波减速器核心部件结构应力分析
[J].
Structural stress analysis of the core components of harmonic reducer
[J].
双圆弧谐波齿轮传动齿廓设计与参数分析
[J].
Double-circular-arc tooth profile design and parametric analysis of harmonic drive
[J].
不同共轭原理的双圆弧齿廓谐波齿轮传动分析
[J].
Double-circular-arc tooth profile of harmonic drive analysis based on different conjugate principle
[J].
在响应曲面方法中三类中心复合设计的比较研究
[J].DOI:10.3969/j.issn.2095-1248.2007.01.026 [本文引用: 1]
A comparative study of three central composite designs in response surface methodology
[J].DOI:10.3969/j.issn.2095-1248.2007.01.026 [本文引用: 1]
径向变形量对谐波减速器啮合特性及柔轮应力的影响分析
[J].
Influence of radial deformation on stress of flexspline and meshing characteristic of harmonic reducer
[J].