全断面岩石隧道掘进机（tunnel boring machine，TBM）具有施工效率高、安全可靠、劳动强度低、环境污染小等优点，被广泛应用于铁路、水利、水电、国防等隧道工程^[1-3]. 特别是近10年来，随着隧道建设和地下工程的蓬勃发展，我国TBM施工技术和自主研发水平获得迅猛发展^[4-7]. 敞开式TBM由于其盾体较短、护盾收缩灵活等特点，在超前地质处理、快速支护、应对卡机风险等方面具有独特优势^[8-9]. 在敞开式TBM掘进过程中，除了起防护作用外，护盾可以通过撑紧洞壁减小振动、稳定刀盘^[10]. 随着滚刀磨损和更换，TBM开挖洞径会在一定范围内变化. 护盾半径的设计既要满足TBM良好的通过性，又要保证与洞壁的可靠接触^[11].

TBM工作环境恶劣，由于地质复杂多变，曾多次发生卡盾事故，护盾挤压变形严重，极大影响了施工进度^[12-13]. 近年来，许多学者研究了围岩变形对护盾的影响. Hasanpour等^[14]提出过度切削对盾体和地层之间的关系的影响. 程建龙等^[15]使用数值模拟方法分析了挤压和位移释放对护盾压力的影响规律. 刘泉声等^[16]提出了一种监测TBM护盾变形方案，计算得出护盾受力模型. 刘泉声等^[17] 提出了一种监测护盾变形方案以及护盾受力计算方法，根据护盾变形进行卡机状态监测，并提出了对应的处理措施. 上述研究主要集中于双护盾TBM的护盾变形和受力分析，对敞开式TBM护盾设计鲜有提及.

目前，敞开式TBM护盾半径的设计主要依靠经验，缺乏深入的理论研究. 本文分析现有敞开式TBM护盾结构形式，建立护盾与洞壁之间的接触理论模型，研究护盾与洞壁之间接触间隙的变化规律，结合护盾运动规律分析和有限元力学性能分析，分别对顶护盾、侧护盾、底护盾进行半径的适应性设计，为TBM护盾半径设计提供理论依据.

敞开式TBM的护盾主体为钢结构焊接件，一般由6块盾体组成，分别为顶护盾，顶左、右侧护盾，底左、右侧护盾和底护盾，如图1所示. 护盾围绕在机头架周边，除底护盾外，其他护盾均可以自由伸缩以适应不同开挖洞径，如图2所示. 当TBM掘进作业时，各个护盾撑紧在洞壁上以稳定刀盘，同时防止大块岩渣掉落在刀盘后部及主驱动电机处.

由于安装位置不同，各个护盾的结构设计与功能具有不同特点. 顶护盾通过中间导向柱和两侧的油缸与机头架连接，由油缸的伸缩控制实现盾体的上下伸缩. 顶左、右侧护盾上部与顶护盾通过销轴连接，下部搭接在底左、右侧护盾上，跟随顶护盾与底侧护盾的运动实现伸缩. 顶护盾与顶侧护盾基本覆盖了顶部大部分区域，对安全施工尤为重要. 底护盾通过螺栓与机头架连接，承受主机重力，同时可以作为支点辅助主机调向. 底左、右侧护盾通过销轴与底护盾连接，在油缸作用下绕销轴转动，上部通过楔块锁紧装置将侧护盾的位置牢牢锁定，保证护盾与洞壁可靠支撑.

如表1所示为部分工程项目所采用的TBM护盾尺寸. 其中， ${R_{\rm n}}$为TBM安装新刀时的开挖半径，R_f为顶护盾半径，R_fs为顶侧护盾半径，R_bs为底侧护盾半径，R_b为底护盾半径. 总体而言，护盾半径设计主要有各护盾等尺寸设计和各护盾针对性设计2种策略. 相对于开挖洞径 $R$，顶护盾半径R_f一般相对R_n缩小40~100 mm；顶侧护盾半径R_fs和底侧护盾半径R_bs一般相对R_n缩小40~50 mm；底护盾半径R_b一般相对R_n缩小40~50 mm或者等于隧洞理论最小开挖半径R_w。总体而言，护盾半径设计主要有各护盾等尺寸设计和各个护盾针对性设计2种策略.

由于护盾尺寸设计的差异，底侧护盾与底护盾安装后呈现不同的位置关系，如图3所示. 图3（a）：底侧护盾相对于底护盾向内收缩20 mm以上，导致底侧护盾与洞壁间隙过大，影响盾体受载状态；图3（b）：底侧护盾相对于底护盾突出20 mm以上，可能导致底侧护盾下部与洞壁干涉，造成护盾转动不畅和盾体磨损；图3（c）：底侧护盾与底护盾整体齐平，其使用性能和美观度均较好.

理想情况下，护盾与洞壁均匀接触，此时载荷分布均匀，接地比压小. 但是在实际施工中，TBM开挖洞径随着边缘滚刀的磨损而逐渐减小，需要在磨损量超过15 mm之前更换边滚刀，以保证隧道的最小开挖洞径. 因此，隧道洞壁半径R是在R_n和R_w之间不断变化的. 在特殊情况下，需要对隧洞进行扩挖作业，使洞径增加. 护盾半径的设计需要适应不同的洞径尺寸，以获得最佳的接触状态和使用效果.

底侧护盾与底护盾之间通过销轴连接，在护盾油缸作用下绕销轴转动. 随着开挖状态的改变，护盾通过伸缩适应不同的开挖洞径，以有效支撑开挖洞壁. 护盾半径必然无法与开挖洞壁半径保持一致，因此护盾外圆与洞壁圆弧理论上呈现线接触状态，接触点位置由护盾位置与尺寸决定.

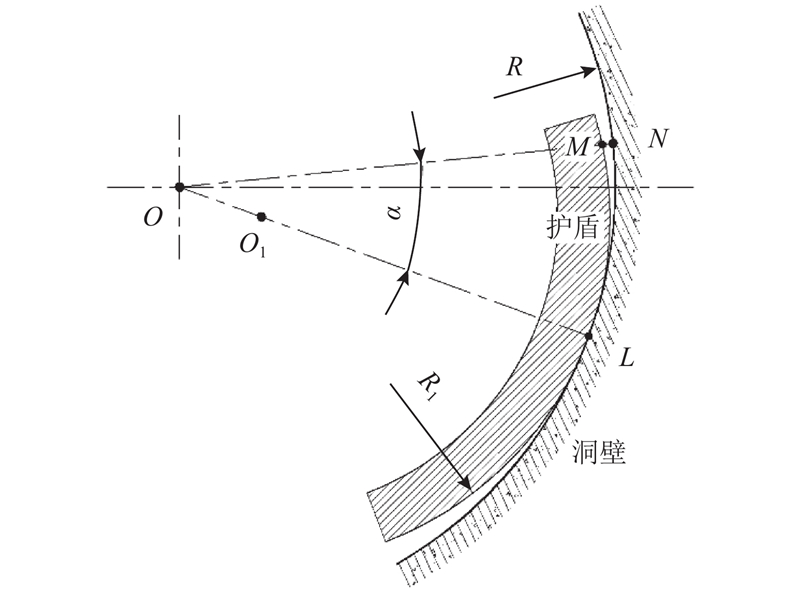
将底侧护盾与洞壁的位置关系进行简化，如图4所示. 点H表示护盾销轴位置，点O表示洞壁圆心，护盾最底部点D与销轴点H距离很近，在转动过程中其位置基本不变. 为避免该处与洞壁接触，同时考虑制作误差，应保证该点与最小洞壁有5~10 mm的间隙.

当护盾绕点H旋转时，必有一点首先接触洞壁，设为点A. 连接点A与护盾最低点D，作AD中垂线，护盾圆心必在此中垂线上. 作直线AO与AD中垂线相交于点O₁，当以该点作为护盾圆心时，护盾与洞壁相切于点A，护盾半径小于洞壁半径. 当洞壁半径缩小为R'时，护盾绕点H收缩，护盾圆心位于以HO₁为半径的圆弧上. 以洞壁中心点O为圆心，以R'与R₁的差值为半径作圆，与圆弧 ${A_{H{O_1}}}$相交于点 ${O_1}^\prime $，该点即为护盾与当前洞壁相切时护盾圆心所处位置. 此时护盾与洞壁相切于OO₁延长线与洞壁的交点（点C）.

选取图4中的点O₂作为护盾圆心，护盾半径缩小，此状态下护盾与洞壁在点A以下部分区域已经干涉，表明点A以下某区域一点先于点A接触洞壁，如图5（a）所示. 此时护盾半径过小，护盾与洞壁切点位置过低，楔块对应区域与洞壁存在较大间隙，导致上部区域悬空，护盾承受附加弯矩，护盾受载情况恶劣. 若选取O₃作为护盾圆心，护盾半径增大，此时点A以上区域与洞壁已经干涉，表示护盾点A以上区域某点先于点A接触洞壁，若接触点超越点B，则护盾与洞壁相交于点B，如图5（b）所示. 此时护盾半径过大，护盾与洞壁不存在相切点，即护盾最上部与洞壁首先接触，该情况先对护盾受载不利，同时易造成围岩扰动. 合理的护盾半径设计，应保证当护盾随着洞径改变而伸缩时，其与洞壁的接触区域位于水平线附近，此处为楔块施力位置，护盾整体受力情况好，如图5（c）所示.

如图6所示，护盾与洞壁在某点L接触后，从该点向两侧区域间隙逐渐对称增大. 以洞壁中心点O为中心，以直线OL为基准偏移某任意角度 $\alpha $作直线，该直线与护盾和洞壁分别相交于点M和点N. 采用 $s$表示护盾与洞壁间隙MN， ${R_1}$为护盾半径，可以获得 $s$的表达式如下：

式中：h为开挖半径R与护盾半径 ${R_1}$的差值. 为方便起见，将上述函数表示为如下形式：

实际开挖洞壁轮廓虽然相对粗糙，但整体开挖尺寸在理论开挖洞径附近波动. 本模型采用理论开挖洞壁作为分析对象，通过上述函数关系可以获取各变量的相互影响规律.

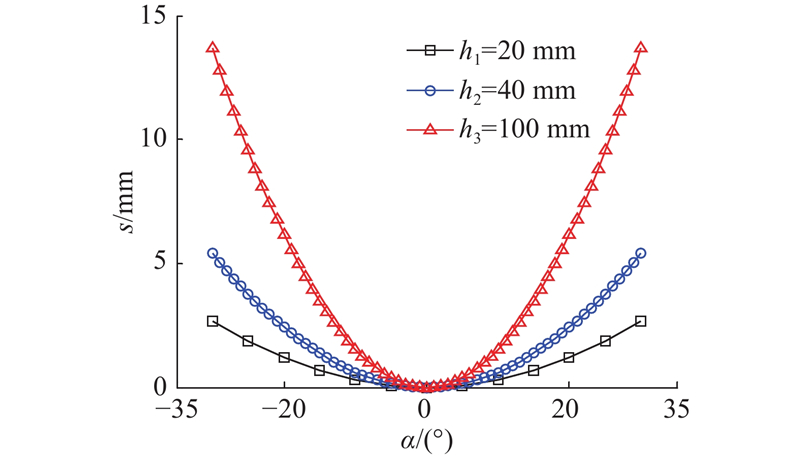
以9 030 mm洞径为例，即R=4 515 mm，分别取h₁=20 mm，h₂=40 mm，h₃=100 mm，即护盾半径分别为4 495、4 475、4 415 mm. 依据式（1）可以获得护盾与洞壁间隙s随位置角度α的变化曲线，如图7所示. 在同一护盾半径条件下，随着护盾位置由切点向两侧偏移，护盾与洞壁间隙逐渐增大，且间隙增加幅度也逐渐增大. 护盾与洞壁半径差越大，相同角度α条件下护盾与洞壁间隙越大，并且护盾与洞壁间隙变化幅度随着角度α变化而增大.

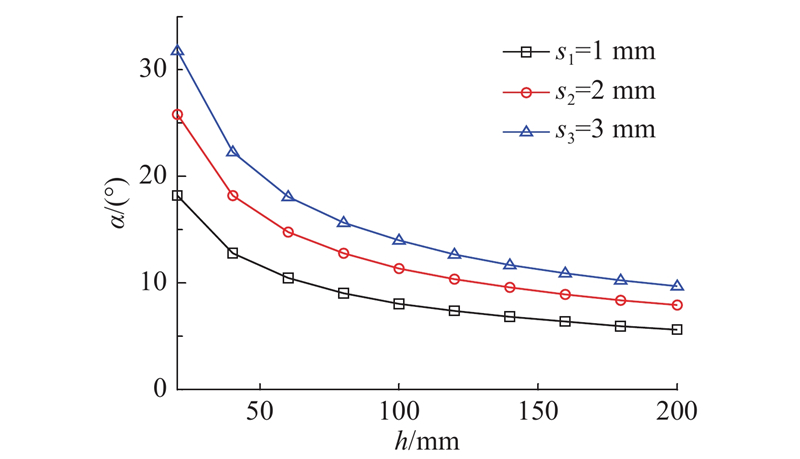
如图8所示为护盾间隙与对应位置角度α的变化曲线. 相同护盾半径下，随着护盾与洞壁间隙量增加，对应角度α增大. 在相同间隙条件下，不同半径护盾对应不同的角度α. 如在护盾与洞壁间隙为1 mm的条件下，当护盾半径相对洞壁半径缩小20 mm时，对应角度为18.2°. 随着护盾半径差不断增加，对应角度α先急剧减小，后逐渐趋于平缓. 在半径缩小200 mm时，对应位置角度α减小到5.6°.

在不同洞径条件下，不同参数选择的计算结果会略有差异，但均呈现上述相同的变化规律. 即在任意开挖洞径条件下，护盾与洞壁间隙均由切点位置向两侧逐渐增大. 护盾半径缩小量越大，在相同位置角度 $\alpha $对应的间隙越大. 在指定间隙范围内，护盾半径缩小量越小，其角度覆盖范围越大.

上述理论分析可以为护盾半径设计提供指导. 仍以某9 030 mm洞径为例加以说明. 洞壁最大开挖半径为4 515 mm，最小开挖半径为4 500 mm. 假定在销轴位置、护盾大体尺寸等边界条件初步确定的情况下对护盾半径进行选择. 其中，护盾外圆最下部点与最小洞壁间保持5 mm的间隙，该点和点O的连线与隧道水平线呈63.1°. 护盾最上部点和点O的连线与隧道水平线呈15.6°，护盾外圆弧整体覆盖角度为78.7°.

1）护盾半径上限.

在任何洞径条件下，护盾与洞壁接触时应处于相切状态. 在洞壁最大半径为4 515 mm时，护盾伸出量最大，此时应保证护盾外圆与洞壁切点不超出护盾最上部点. 选取护盾最上部点为切点，则护盾最下部与最大洞壁间隙s=20 mm，护盾最下部点和点O的连线相对该切点和点O的连线的角度α=78.7°. 可以采用上述作图法或者依据式（2）求得护盾半径差h =25 mm，护盾半径最大值R_max=4 490 mm，护盾半径设计不应超过该值.

为了避免卡机、侵限等问题，一般在原开挖洞径基础上增加一定尺寸的刀盘扩挖量，在部分围岩收敛地段进行扩挖掘进. 本列中，考虑半径方向扩挖量50 mm，则洞壁最大半径为4 465 mm，依据上述计算方法可以获得护盾半径最大值为4 478 mm.

2）护盾半径下限.

当洞壁半径缩小到4 500 mm时，护盾收缩，护盾与洞壁接触点下移. 护盾半径越小，护盾与洞壁接触点越低，对护盾受载情况越不利. 当以上述最大半径4 490 mm设计护盾时，针对4 500 mm洞径，当以上述最大半径4490 mm设计护盾时，针对4 500 mm的开挖半径，计算可得护盾与洞壁接触点位于隧道水平线沿点O向下方旋转3.2°方向上. 可见即使以最大允许尺寸设计护盾半径，护盾与洞壁接触点仍位于水平线以下位置. 但是在该接触点以上区域，护盾与洞壁最大间隙为0.5 mm，对应角度为18.8°；在该接触点以下区域，当护盾与洞壁间隙为1 mm时对应的位置角度为25.8°，护盾与洞壁间隙为2 mm时对应的位置角度达36.8°. 因此，护盾与洞壁间隙在大范围内均处于较小间隙状态.

护盾与洞壁理论上虽为线接触状态，但是在工作状态下，护盾与岩壁均会发生不同程度变形，而岩壁实际开挖面并不平整，因此在一定小间隙范围内护盾与洞壁实际处于接触状态. 当护盾半径缩小时，接触点将进一步下移，考虑到实际接触状况，应保证水平线附近位置间隙量不宜过大.

以水平线为参照，选定2 mm间隙视为可接触状态，与护盾最底侧位置间隙联合求解，可以获得护盾对应半径尺寸. 建立方程式如下：

式中：R=4 500 mm，s₁=2 mm，s₂=5 mm，β=63.1°，求解得h=26 mm，即护盾半径最小值R_min=4 474 mm.

综上所述，护盾半径范围为4 474 ~4 490 mm，考虑单边50 mm扩挖量时护盾半径最大为4 478 mm，因此，护盾实际设计值选择4 475 mm.

采用ANSYS/workbench建立底侧护盾与洞壁的接触模型，如图9所示. 洞壁半径取4 515 mm，采用刚体约束. 护盾半径分别取4 475 mm和4 115 mm，护盾宽度为4 500 mm. 接触模型详细参数如表2所示. 表中，s_b为护盾对底部与洞壁的间隙，s_h为护盾水平位置与洞壁的间隙，α_h为护盾与洞壁接触点与水平线的夹角.

在护盾楔块作用平面施加的载荷由油缸载荷经楔块放大后获得，本模型施加的最大载荷为400 kN，方向垂直该平面. 在该力作用下护盾绕销轴转动，与洞壁接触，洞壁内圆采用固定约束. 分别获得2种护盾的最大应力，如图10所示. 图10（a）中施力面和洞壁反作用力位置均在水平线附近区域，护盾变形主要集中在该区域范围，最大应力为25.7 MPa. 图10（b）中护盾施力面为楔块作用平面，反作用力面位于水平线绕点O向下方旋转45.7°方向处，由此引入附加弯矩，护盾大变形区域为该反作用力区域，最大应力为363.2 MPa.

护盾材料选用Q345材料，采用厚板焊接，屈服应力为275 MPa. 护盾a最大应力远小于材料屈服应力，设计满足要求. 护盾b最大应力远超材料屈服强度，为不合理设计. 可见，护盾半径设计不仅是尺寸的差异，还会对护盾载荷产生极大影响.

当顶护盾半径大于洞壁开挖半径时，护盾两侧会与洞壁先接触，护盾与洞壁接触状态不佳，易于对围岩造成扰动. 当护盾半径等于洞壁开挖半径时，护盾与洞壁均匀接触，贴合状态最好. 由于洞顶应力较大，围岩容易收敛，护盾实际设计半径会比最小开挖半径略小. 此种情况下，护盾与岩壁间存在间隙，间隙变化规律仍可采用式（2）表示，区别在于其接触点位置始终位于洞壁竖直中心线处.

如图11所示，护盾与洞壁最大间隙出现在两端位置，下文以单边对应角度 $\alpha = 30^\circ $为例加以说明. 现阶段TBM开挖直径多为3 000~10 000 mm，本文选取R=1 000~5 000 mm进行分析.

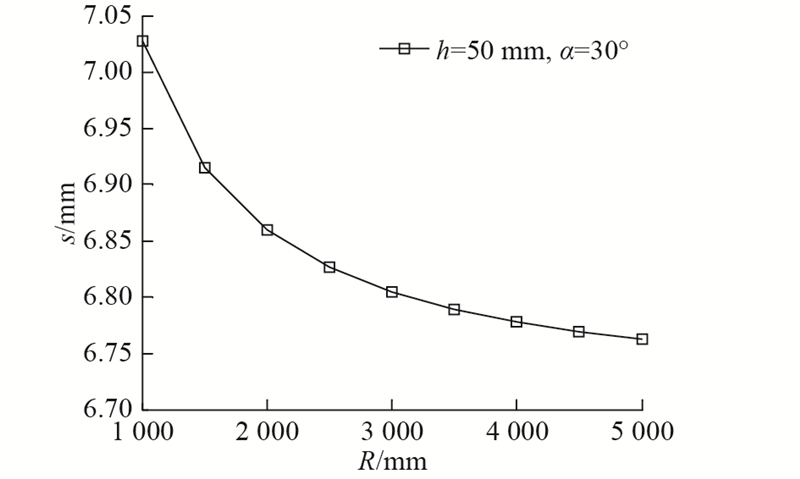
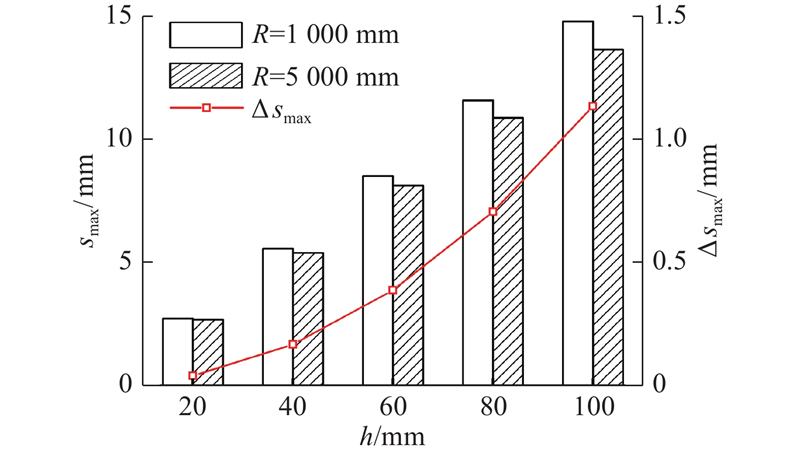
针对不同洞径范围，当护盾缩小量一定时，洞壁与护盾最大间隙量会出现差异. 例如当护盾半径相对于洞壁缩小量为50 mm时，随着开挖洞径增大，护盾与洞壁的最大间隙逐渐变小，如图12所示. 护盾与洞壁间隙最大值为7.02 mm，最小值为6.76 mm，间隙差为0.26 mm，可见不同洞径对应的间隙差距很小. 如图13所示为开挖洞壁半径为1 000与5 000 mm时对应的护盾间隙量对比，其间隙差异量随着护盾与洞壁半径差的增大而增大，但是相同半径差条件下2组间隙差异量均较小。 如在护盾与洞壁半径差h=20 mm时，2种洞壁半径对应的间隙差异量为0.04 mm. 在h增加到100 mm时，间隙差异量增加到1.13 mm，但是仅占1 000 mm洞壁对应间隙量13.65 mm的8.3%. 可见针对不同的开挖洞径，当采取相同的半径缩小量设计护盾时，护盾与洞壁的接触间隙基本一致.

由于开挖半径随着滚刀磨损变化，最大洞壁半径与最小洞壁半径一般存在15 mm的差异量，导致同一护盾尺寸下，其相对于洞壁的最大间隙在一定范围内变化. 仍以9 030 mm洞径为例，最大开挖半径为4 515 mm，最小开挖半径为4 500 mm，取 $\alpha = 30^\circ $. 在护盾半径比最大开挖半径小50 mm时，护盾与最大开挖洞壁的最大间隙为6.76 mm，护盾与最小开挖洞壁的最大间隙为4.72 mm，间隙差值为2.04 mm. 基于式（2）可以求得，当洞壁半径为1 000~5 000 mm时，护盾相对最大开挖洞径缩小20~100 mm，护盾与最大开挖洞壁和最小开挖洞壁的间隙差为2.01~2.41 mm.

在任何开挖洞径条件下，相对于开挖洞径，当护盾半径缩小量选取30~50 mm时，护盾与洞壁最大间隙为4~7 mm. 随着滚刀磨损，洞壁半径缩小15 mm后，护盾与洞壁最大间隙仍为2.0~4.8 mm. 因此，顶护盾半径缩小量控制在此范围较为合理，如表1中所列西秦岭、高黎贡山、锦屏等项目. 若护盾半径缩小量过大（如：达到100 mm），护盾与洞壁最大间隙达13 mm以上，对护盾承载不利.

底护盾用于承受主机前端压力，需要提供有效支撑，其不具备伸缩功能，需要保证底护盾能顺利通过最小开挖洞壁.依据上述基本原则，底护盾半径设计值一般等于最小开挖半径，此时护盾与刀盘同心安装，即理论上护盾外圆与最小开挖洞壁重合。底护盾半径也可以小于最小开挖半径，但是应保证护盾底部与最小开挖洞壁底部重合，此时护盾与刀盘不同心，护盾两侧与洞壁间出现微小间隙，该间隙量变化规律同顶护盾一致. 无论选择何种方案，在开挖洞径大于最小开挖洞径时，护盾底部与洞壁间都将存在间隙，此间隙由刀盘开挖产生的浮渣填充. 因此，底护盾设计在保证底部与最小开挖洞壁底部重合前提下，护盾半径相对于开挖半径可缩小15~50 mm，如表1所示的不同项目中底护盾尺寸属于合理设计.

（1）研究了底侧护盾与洞壁的接触状态，获得了护盾与洞壁接触间隙变化规律关系. 底侧护盾设计应保证最下部与最小洞壁保持5~10 mm间隙，在水平位置附近与洞壁相切接触. 基于护盾与洞壁接触位置和间隙理论计算，提出了底侧护盾半径的设计方法.

（2）顶护盾半径应比开挖半径小30~50 mm，护盾与洞壁最大间隙出现在护盾两端，该间隙主要由护盾半径相对于洞壁半径的缩小量决定，开挖洞径本身大小对其影响微小. 当护盾半径一定时，护盾与洞壁间的最大间隙随着开挖半径的增大而增大.

（3）底护盾半径设计应保证护盾底部与最小开挖洞壁底部接触，护盾半径相对于开挖半径可缩小15~50 mm，护盾与洞壁的间隙变化规律同顶护盾一致.