水泥净浆通常被认为是一种宾汉姆流体[4-6];同时,水泥净浆具有触变性[7-11],是一种剪切变稀的流体,在剪切作用下,其表观黏度会下降. Hattori等[12-13]认为水泥净浆的表观黏度与单位体积的可逆键连接数量有关,并将单位体积的可逆键连接数表示成了剪切速率和絮结速率以及时间的函数,建立了服部-泉理论(Hattori-Izumi theory,HI理论). Wallevik等[14-15]对上述函数进行了修正,用2个记忆模量代替了剪切速率和絮结速率,同时对屈服应力和表观黏度的计算方式进行了修正,建立了修正的HI理论,即颗粒流交互理论(particle flow interaction theory,PFI理论).
基于理论流体力学,本文提出一种迭代算法,用于快速计算回转黏度仪流场中水泥净浆的流变特性参数,以及水泥净浆PFI参数的标定. 针对此类非线性流场,本文根据回转黏度仪中水泥净浆流场中心对称的性质,对流场进行径向分层,假设层内的流体具有均匀性和连续性,对每层运用雷诺-里符林公式计算剪切速率,进而计算出整个流场中水泥净浆的流变特性参数.
1. 理论分析
水泥净浆的黏度主要受时间、剪切和温度等因素的影响. 本文研究当温度为20~25°C时,在回转黏度仪叶片剪切作用下,水泥净浆的表观黏度在流场中的分布和变化情况.
1.1. 水泥净浆的流变特性与参数测定
流变性是指物质在外力作用下的变形和流动性质,对于流体来说,就是施加于流体上的剪切应力
按照是否符合牛顿内摩擦定律,可以将流体分为牛顿流体和非牛顿流体. 牛顿流体是一种流变性与时间无关的纯黏性流体,其流变方程为
式中:
在非牛顿流体中,按照流变性是否与剪切持续时间相关,可以把非牛顿流体分成2类:非时变性非牛顿流体和时变性非牛顿流体. 静态下水泥净浆的近似流变模型—宾汉姆流体即为一种非时变性非牛顿流体,其流变方程如下:
式中:
在非牛顿流体中,剪切应力与剪切速率的比值被定义为黏度
由式(3)可知,表观黏度是一个与剪切速率
宾汉姆流体的流变特性参数可通过回转黏度仪测定,对于回转黏度仪存在以下公式:
式中:
式中:R1、R2分别为黏度仪内、外筒半径,
雷诺-里符林公式为给定内筒转速下回转黏度仪水泥净浆流场中不同半径处的剪切速率计算提供了方法.
1.2. HI理论及PFI理论
水泥净浆具有触变性,即水泥净浆的黏度会在持续的剪切作用下渐渐变小,剪切作用消失后,黏度会逐渐恢复.
Hattori[12]从微观结构出发,对水泥净浆的触变性作出了如下解释:在水泥与水的水合反应过程中,相互接触的颗粒之间会出现絮结,形成连接键,由范德华力形成的连接键可被剪切破坏,称为可逆键,由于水合反应形成的连接键不可被剪切破坏,被称为不可逆键. 在受到剪切作用时,水泥净浆中的可逆键被破坏,水泥颗粒重新成为自由粒子,在宏观上导致水泥净浆的黏度减小,呈现剪切变稀的性质. 剪切作用消失后,由于范德华力的作用,自由的水泥颗粒之间会形成可逆连接键,宏观上导致水泥净浆的黏度逐渐恢复.
HI理论认为水泥净浆的表观黏度与单位体积的可逆键连接数量有关,即
式中:
式中:
由式(6)和式(7)得到表观黏度为
由于剪切速率
1)用2个记忆模量
式中:
其中,
2)修正屈服应力和表观黏度的计算方式. 塑性黏度和屈服应力的计算公式如下:
式中:
3)修正絮结速率的计算方法,计算公式如下:
式中:l为一个经验常数,恒等于1 s−2. K(t)为经验函数,计算方法如下:
PFI理论将水泥净浆的塑性黏度和屈服应力表示成了剪切速率和时间的函数,为受剪切作用时水泥净浆的黏度和屈服应力的计算提供了方法,参数
基于以上理论,本文所述迭代算法先通过雷诺-里符林公式计算流场中不同半径处的剪切速率,再通过PFI理论计算流场中不同半径处的塑性黏度和屈服应力.
2. 数值计算方法
在采用回转黏度仪测量水泥净浆的流变特性时,转子运动带动附着于其表面的水泥净浆运动,在整个测量区域内形成流场. 通过雷诺-里符林公式可以推导出整个流场区域内的剪切速率的计算公式如下:
式中:
由式(18)可见,测量区域中的剪切速率
2.1. 有限差分仿真计算
Wallevik[16]利用有限差分法,结合PFI理论对回转黏度仪中的水泥净浆流场进行了仿真,利用Taylor展开,取一阶截断,得到如下公式:
式(19)被称为空间中心差分,对整个流场区域进行网格划分,在格点上应用式(19)得到速度的更新公式(式(20)). 如图1所示,v为每个网格点的速度,i为黏度仪转子半径方向的单位向量,j为黏度仪转子轴向.
图 1
式中:
式中:
Wallevik[16]比较了有限差分方仿真结果与试验结果,发现仿真曲线与试验曲线相似度极高,验证了有限差分方法仿真的准确性.
在每个时间步长内,需要对流场区域内的速度、转矩、黏度等参数进行计算,以得到一个收敛的解. 如果得到的计算结果不收敛,则本次仿真失败,需要使用更小的时间步长进行仿真. 因此整个仿真的耗时较长,效率较低,很难满足实验时标定水泥净浆的PFI参数的要求.
2.2. 二维迭代计算方法
针对三维仿真计算存在的问题,根据回转黏度仪内部的水泥净浆运动特性,提出二维状态下回转黏度仪内部各点黏度及剪切速率计算方法.
首先对回转黏度仪的结构及其测量区域内水泥净浆的流动状态进行分析. 为了提高黏度仪的测量精度,黏度仪转子通常采用上、下部分离结构,如图2所示.
图 2
图 2 回转黏度仪转子结构示意图
Fig.2 Schematic diagram of rotor strcture in rotational viscometer
回转黏度仪在采集数据时,只采集转子上部的数据. 由于机械结构的分离,转子上、下部分由不同的驱动结构带动,转子下部复杂的流场分布对转子数据采集的影响被消除. 在这种状况下,可以认为对于转子上部而言,从上至下,流体对转子的作用力是均匀的,因此可以通过流场区域的径向分层来简化计算过程.
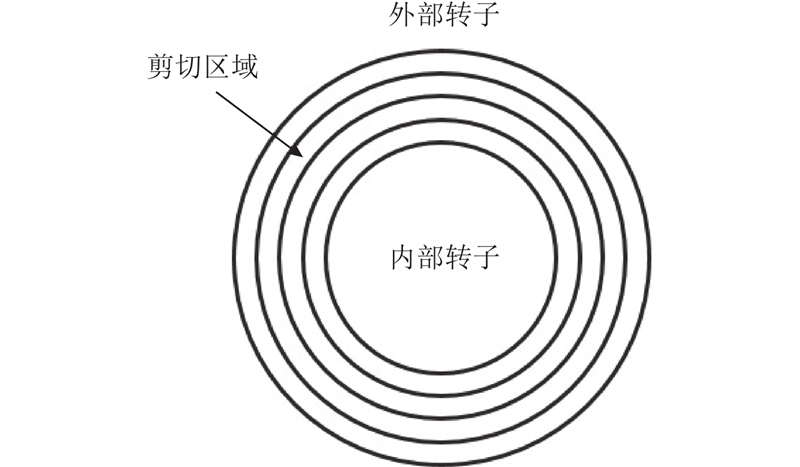
如图3所示,基于回转黏度仪流场中心对称的特性,在黏度仪半径方向上,将流场划分为许多很薄的剪切层,并认为划分之后的剪切层符合以下条件:
图 3
图 3 黏度仪流场区域径向分层示意图
Fig.3 Radial stratification diagram of viscometer flow field
1)可认为层内流体的流体特性(黏度和屈服应力等)相同;
2)层与层之间接触部分的转速相同;
3)整个流场区域内所有的剪切层受到的转矩为同一值(转子转动的驱动转矩).
4)转子表面的流体与转子转速相同.
根据以上条件可以构建简单的迭代算法,在层内运用雷诺-里符林公式计算剪切速率,当整个流场符合以上4个条件时,即可认为迭代算法收敛,计算得到的转速符合实际流场的剪切运动. 具体计算步骤如图4所示.
图 4
图 4 单个时间步内黏度仪流场更新流程图
Fig.4 Update flow chart of viscometer flow field in single time step
在仿真过程中,流场中计算得到的转速分布状况有4种,不同转速分布状况的处理方式如下.
1)若转速由内至外不断减小且均为正值,最外层的转速小于阈值,则可认为本次选取的转矩值与真实流场的转矩值误差在可接受范围内,停止迭代.
2)若转速由内至外不断减小且均为正值,最外层的转速大于阈值,则可认为本次选取的转矩值小于真实流场的转矩值,须根据误差增大转矩值.
3)若转速由内至外不断减小,出现转速为负的状况,则可认为本次选取的转矩值大于真实流场的转矩值,须根据误差减小转矩值.
4)若转速由内至外增加,则说明转速太小,靠近外部的水泥净浆由于所受剪切应力小于屈服应力而静止,此时认为出现阻塞流,须将出现阻塞流位置的半径作为外筒半径代入算法,重新计算转矩.
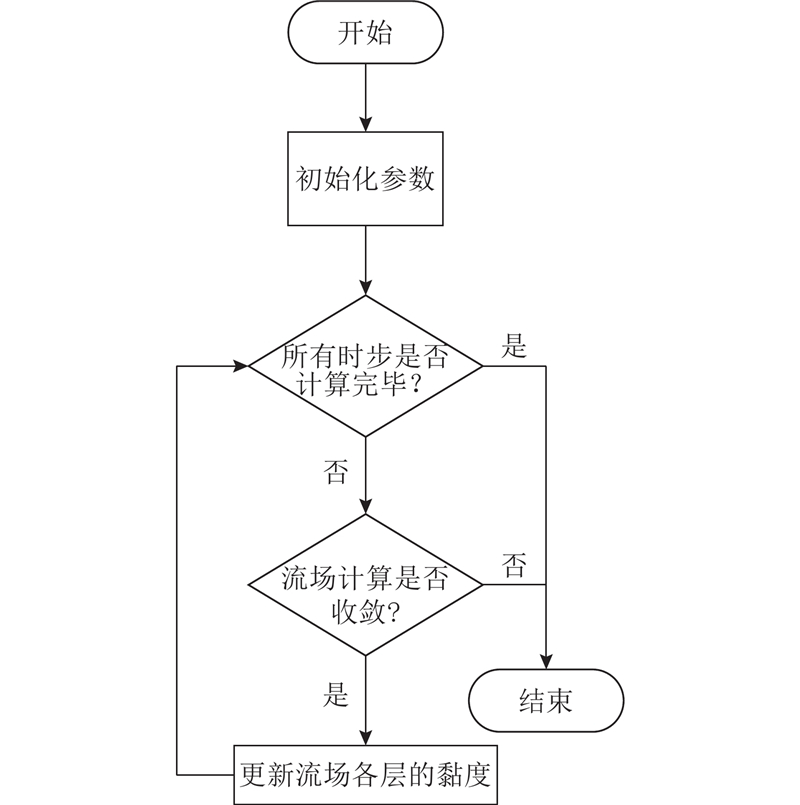
单个时间步的仿真结束后,可以通过PFI理论计算这个时间步的水泥净浆特性,然后根据当前的水泥净浆特性,计算下一个时间步的剪切速率,直至仿真结束,具体步骤如图5所示.
图 5
图 5 黏度仪流场内部流变特性参数更新流程图
Fig.5 Update flow chart of internal rheological parameters of viscometer flow field
3. 仿真结果对比与验证
本文将迭代算法的仿真结果分别与文献[16]中有限差分法的仿真结果以及试验结果进行对比,以验证迭代算法仿真结果的准确性.
3.1. 迭代算法仿真结果与有限差分法仿真结果对比
图 6
表 1 迭代算法与有限差分法仿真参数设置
Tab.1
| PFI参数 | 单位 | 数值 | PFI参数 | 单位 | 数值 | |
| | Pa·s | 0.65 | U0 | − | 1 | |
| a1B3n32/3 | Pa·s | 33 | ma | s | 30 | |
| | Pa | 0 | mb | s | 0 | |
| a2B3n32/3 | Pa·s | 24 | − | − | − |
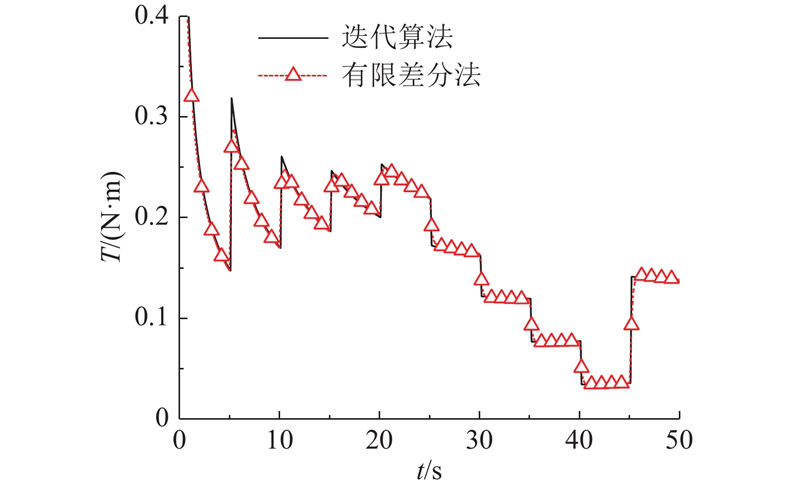
图 7
图 7 迭代算法、有限差分法仿真结果对比
Fig.7 Comparison of simulation results between iterative algorithm and finite difference method
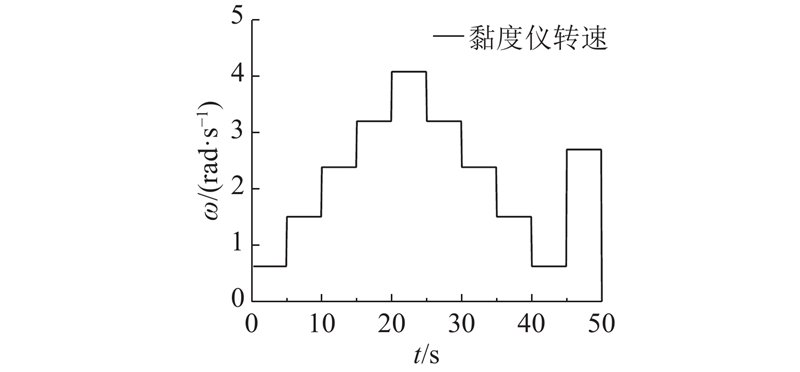
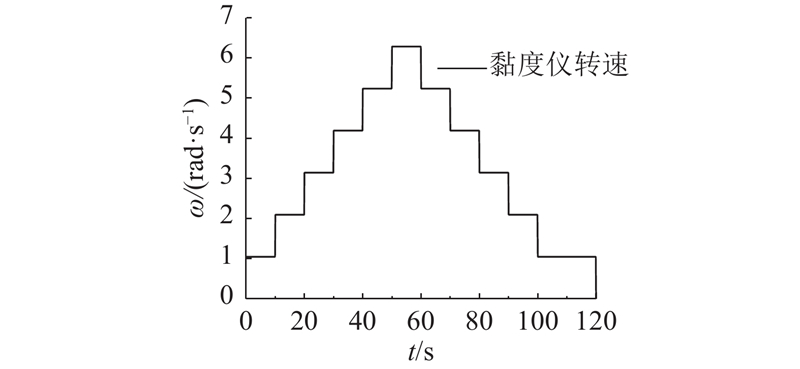
3.2. 迭代算法仿真结果与试验结果对比
表 2 变转速试验迭代算法仿真参数设置
Tab.2
| PFI参数 | 单位 | 数值 | PFI参数 | 单位 | 数值 | |
| | Pa·s | 0.451 8 | U0 | − | 39.259 5 | |
| a1B3n32/3 | Pa·s | 2.220 8 | ma | s | 30 | |
| | Pa | 0.601 9 | mb | s | 0 | |
| a2B3n32/3 | Pa·s | 5.300 0 | − | − | − |
图 8
图 9
图 9 试验结果和迭代算法仿真结果对比
Fig.9 Comparisons between experimental results and simulation results of iterative algorithm
4. 结 语
本文基于PFI理论,提出了一种用于回转黏度仪的水泥净浆流变性分布迭代算法. 该算法采用对流场径向分层的方法,在每层运用雷诺-里符林公式计算剪切速率,并结合PFI理论计算每层的流变性参数,将复杂的三维仿真问题转化为了二维问题,简化了计算过程. 所提算法计算结果与有限差分法仿真结果高度相似,与试验结果的平均误差率为4.23%,计算结果较准确. 相较于传统的有限差分法,该迭代算法将计算时间由5 d缩短到了2.55 s,计算效率较高,可用于水泥净浆PFI参数的实时标定,并对相似的对称流场的宾汉姆流体仿真有一定借鉴价值. 该算法仍存在一定的局限性,在变转速试验转速上升阶段有一定的仿真误差,因此,在后期的工作中须进一步完善转速上升时的计算方式.
参考文献
Deformation and flow. an elementary introduction to theoretical rheology
[J].
Extension of the Reiner-Riwlin equation to determine modified Bingham parameters measured in coaxial cylinders rheometers
[J].
Problems of cross-viscosity
[J].DOI:10.1093/qjmam/5.1.42 [本文引用: 1]
水泥混凝土统一流变模型
[J].
Unified rheological model of cement concrete
[J].
The rheological properties of cement and cement-mortar-stone
[J].DOI:10.1063/1.1745167 [本文引用: 1]
Thixotropy: a general review
[J].DOI:10.1016/0377-0257(79)87001-9 [本文引用: 1]
新拌水泥浆体流变性能及流变模型的探讨
[J].DOI:10.3969/j.issn.1001-1625.2004.06.009
Study on rheological properties and rheological model of fresh cement paste
[J].DOI:10.3969/j.issn.1001-1625.2004.06.009
The origins of thixotropy of fresh cement pastes
[J].DOI:10.1016/j.cemconres.2011.09.004
Thixotropic behaviour of cement pastes
[J].DOI:10.1016/0008-8846(79)90123-6 [本文引用: 1]
Rheological properties of cement paste: Thixotropic behavior and structural breakdown
[J].DOI:10.1016/j.cemconres.2008.10.001 [本文引用: 2]
Microstructure-rheology: thixotropy and workability loss
[J].
Computational partial differential equations: numerical methods and Diffpack programming
[J].
A finite-element method for incompressible non-Newtonian flows
[J].DOI:10.1016/0021-9991(80)90163-1 [本文引用: 1]