在破碎机械中,物料的运动特征对衬板磨损具有显著影响,对此已有一些分析研究[3-4]. 为了准确模拟物料运动,当前最常用的数值计算方法之一是离散单元法(discrete element method,DEM)[5-6]. DEM能够精确计算每一个颗粒的运动[7],且已被广泛应用于破碎设备的仿真模拟. Cleary[8]是采用DEM研究破碎设备的先驱. 针对破碎机械的磨损问题,也有不少学者使用数值方法进行了研究. 比如,Mishra[9]首先使用Millsoft软件研究了半自磨机衬板上的能量分布. Kalala等[10]基于2D的DEM模拟结果研究了衬板上的磨损. Cleary等[11]使用离散单元法研究了衬板设计对HICOM®磨机中磨损行为的影响. Powell等[12]基于离散单元法定性分析了球磨机衬板形状随运行时间的变化. 此外,国内学者同样采用DEM对破碎机械的各种性质进行了研究[13-14],其中也包括磨损问题[15].
本研究采用DEM对比讨论粒径大小对半自磨机衬板磨损的影响,为分析物料粒径分布特点与磨损关系提供理论依据.
1. 数学模型
1.1. 颗粒模型
在DEM中,应用牛顿运动定律来计算颗粒的运动. 具体来说,对某颗粒i,若其质量为mi,转动惯量为Ii,则其平移运动和旋转运动按照下式计算:
式中:vi为颗粒速度,g为重力加速度,ni为与颗粒碰撞的所有颗粒以及壁面的数量,ωi为颗粒角速度,
其中,kn、kt为法向和切向弹性系数,ηn、ηt分别为法向和切向阻尼系数,
其中,fs为滑动摩擦系数. 本次研究将颗粒形状简化为球形,因此只需要计算切向力矩:
其中,n为法向单位向量,r为球形颗粒的半径.
1.2. 磨损模型
由于SIEM磨损模型的准确性已验证[19],本文直接使用该模型来预测磨损:
其中,t0、t1分别为碰撞开始和接触的时间. 注意当
2. 数值方法
2.1. 研究对象
图 1
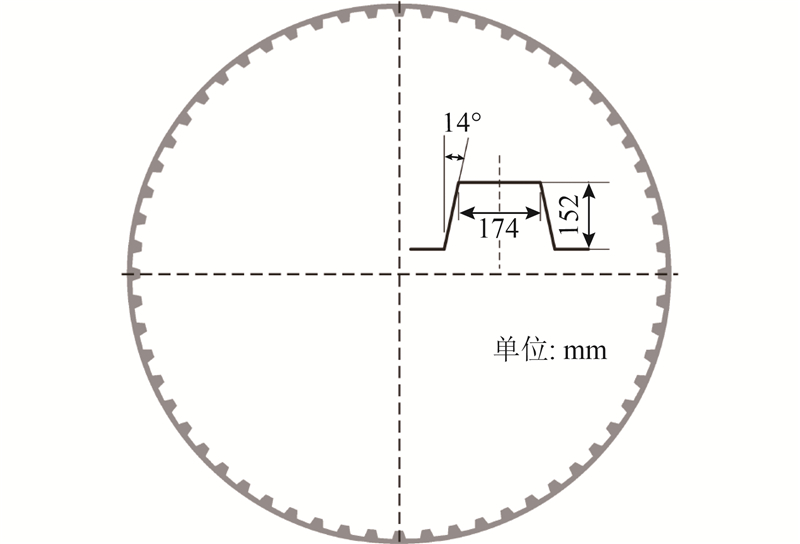
图 1 模拟中所用半自磨(SAG)机结构尺寸示意图
Fig.1 Sketch map of geometry of semi-autogenous grinding(SAG)mill used in simulations
2.2. 参数设置
本研究使用自主开发的DEM软件DEMSLAB来计算半自磨机中物料的运动. 所有物料在模拟时均简化为球形处理,其中使用的钢球直径按实际情况设置为125 mm. 因此,在所有算例中,钢球对衬板磨损的影响均叠加同样计入总磨损中. 由于模拟方法的准确性已经获得了验证,本次研究目标为分析清楚物料粒径对衬板磨损的影响. 因此,5个算例从小到大依次使用5个级别的粒径(最小粒径算例颗粒数量约为500 000),每个算例中粒径在较小的范围内随机分布,分别为25~35,35~45,45~75,75~125,125~175 mm. 滑动摩擦系数、恢复系数等参数则参考了其他研究者的工作[8],具体见表1. 实际计算时,首先使半自磨机运转4圈以确保其内的物料运动达到准稳态,然后再运转4圈以获得磨损预测结果. 计算中使用的时间步长为5×10−5 s.
表 1 半自磨(SAG)机衬板磨损模拟中使用的各项参数
Tab.1
| 参数 | 符号 | 数值 | 单位 |
| 衬板维氏硬度 | HV | 370 | N/mm2 |
| 衬板长度 | − | 0.7 | m |
| 提升条高度 | H | 152 | mm |
| 提升条数量 | − | 60 | − |
| 颗粒密度 | ρ | 4 500(矿石), 7 800(钢球) | kg/m3 |
| 颗粒维氏硬度 | HV | 160(矿石),370(钢球) | N/mm2 |
| 矿石之间的恢复系数 | eP-P | 0.3 | − |
| 矿石与钢球以及衬板间恢复系数 | eP-L | 0.5 | − |
| 钢球与衬板间恢复系数 | eB-L | 0.8 | − |
| 滑动摩擦系数 | fs | 0.5 | − |
| 法向弹性系数 | kn | 2.8 × 106 | N/m |
| 切向弹性系数 | kt | 8 × 105 | N/m |
| 半自磨机转速 | − | 10.5 | r/min |
| 切片厚度 | − | 0.7 | m |
| 总填充率 | − | 35 | % |
| 钢球填充率 | − | 15 | % |
3. 结果与讨论
3.1. 半自磨机中物料的运动特征
如图2所示,不同粒径大小的物料在半自磨机内的抛落以及泻落状态并无显著差异. 各算例以对应的平均粒径命名. 从图中可以看到,少部分颗粒在被提升条带至脱离区后,以较高的轨迹抛落至左下角衬板处(称为降落点),到达衬板前速度达到12 m/s以上. 大多数物料运动则类似雪崩(称为崩流),在自由面以中等速度(约8 m/s)泻落至左下角衬板处(因与降落点位置有所区别,下文将称为底脚区). 底脚区与脱离区之间存在一层低速颗粒带.
图 2
图 2 物料运动特征示意图(蓝色:0,红色:12 m/s)
Fig.2 Snapshots for behavior characteristics of particles(blue:0,red:12 m/s)
3.2. 粒径大小对衬板磨损的影响
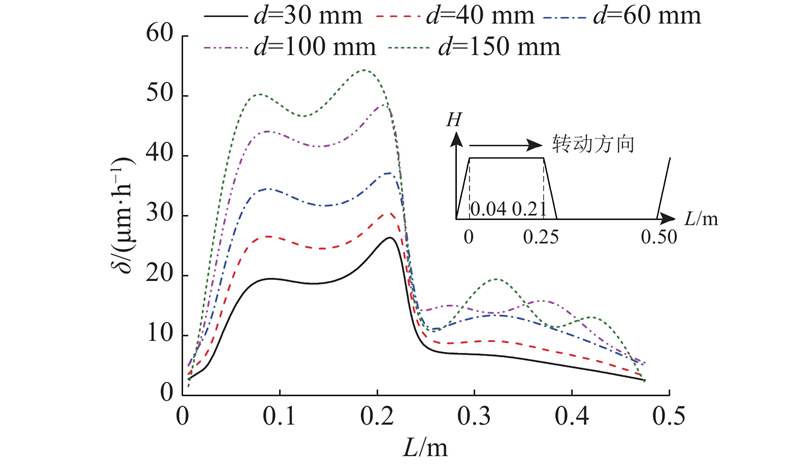
粒径增大,衬板的总磨损速率随之增加. 值得注意的是,总磨损速率并非与粒径大小成正比例关系,当粒径较小时,粒径稍微变大一些(如d从30 mm增加到40 mm)即可显著增加总磨损速率. 反过来可以推测,当粒径进一步减小时,总磨损速率将迅速减小,这直接支持了之前工作中大量小粒径颗粒造成的磨损可以忽略的假设[19]. 图3显示了单块提升条在不同粒径物料作用下的平均磨损率分布曲线. 磨损率大小通过提升条各个位置的磨损体积W,磨机运行总时间t以及各个位置的面积S计算得到. 图中,L 为壁面在单块提升条上的位置. 从图中可以看到,粒径越大,磨损率δ=W/(tS)越大,尤其是提升条上表面的磨损(L=0.03 ~ 0.22 m). 与此同时,也可以清楚地看到提升条上磨损最大值均出现在右上角位置(约0.2 m处),这与实验结果[23]是一致的. 有趣的是,在所有粒径下,提升条上平面左侧(约0.1 m处)磨损率均只比对应的右上角最大值小约5 μm/h. 而在粒径分布范围较大的实际情况下,无论是实验还是模拟结果[19],右上角的磨损远大于上平面左侧磨损. 基于这一结果可以推论得出,在实际物料粒径分布范围较大的情况下,提升条上平面左侧(约0.1 m处)的磨损很可能主要受小颗粒影响而相对较小,右上角处(约0.2 m处)则很可能主要受大颗粒影响而相对较大. 本次研究中,单个粒径分布范围较小,上表面左侧和右上角磨损差异较小.
图 3
图 3 不同粒径大小下单块提升条的磨损曲线图
Fig.3 Wear rate profiles of a lifter under different particle sizes
为了定量分析衬板在磨机内各个位置时的磨损情况,统计平均60个提升条在半自磨机转动过程中,在磨机内圆周不同位置α处的瞬时磨损率R=ΔW/Δt,结果如图4所示. 在计算瞬时磨损率时,需要获得足够短的时间间隔Δt内,提升条上的磨损体积增量ΔW. 这里按照习惯,将半自磨机的顶部设置为0°位置,其余位置按照逆时针方向确定,如图4中的插图所示. 可以清楚地看到,当平均粒径最大(d=150 mm)时,瞬时磨损率在约135°时达到最大值,而当平均粒径最小(d=30 mm)时,最大值位置也略小(约133°). 与图2中结果相比较可知,不同粒径下,提升条磨损仍旧主要发生在进入底脚区时. 随粒径增大,瞬时磨损率最大值也增大(当纵坐标转换为线性坐标时很容易观察到). 此外,随粒径增大,在最大值之后,瞬时磨损率减小得更慢,即减小速率更低. 关于不同粒径下磨损特征的主要原因,将在第3.3和3.4节中详细讨论.
图 4
图 4 不同粒径大小下单个提升条沿SAG机内圆周位置的瞬时磨损率曲线图
Fig.4 Transient wear rate profiles of lifter along circumference of SAG mill under different particle sizes
3.3. 物料运动分析
如图5所示,当粒径不同时,目标区域(如图中插图所示,为沿磨机内圆周105°~175°且宽度为提升条高度2倍区域)颗粒平均速率(
图 5
图 5 不同粒径大小下目标区域内毗邻提升条颗粒的平均速率沿SAG机内圆周位置的分布曲线图
Fig.5 Predicted average speed profiles of particles adjacent to lifters in target region along circumference of SAG mill under different particle sizes
表 2 沿SAG机内圆周110°~170°位置且宽度为提升条高度2倍区域内的颗粒平均平动动能和转动动能
Tab.2
| d/mm | Et / J | J | d/mm | Et / J | J |
| 30 | 1.52 | 0.053 | 100 | 43.50 | 1.850 |
| 40 | 3.67 | 0.146 | 150 | 152.98 | 8.955 |
| 60 | 11.13 | 0.458 | − | − | − |
如图6所示为目标区域内颗粒速率的标准差. 与约120°处平均速率对应,降落点颗粒速率的标准差也更大一些,且在进入底脚区过程中迅速减小,局部极小值的位置也与平均速率的结果几乎一致,因此不再赘述. 值得注意的是在130°~140°内的结果,当粒径较大时(d=150,100 mm),速率标准差SD在达到局部极小值后进入一个短暂的平台期,此后继续逐渐减小,而当粒径较小时(d=60,40,30 mm)则不同,在速率标准差出现极小值后可以观察到一个局部的极大值(约135°处). 在颗粒力学中,一般认为较大的速率标准差意味着颗粒群内部存在更多的剪切. 这一结果表明,在临近提升条磨损发生的主要位置处,小颗粒群内部存在更大的速度梯度,更易发生不同速度的颗粒层之间的滑移. 相比于大颗粒,小颗粒更容易在提升条上表面滑动,这很可能是小颗粒造成的提升条上表面磨损较小的原因之一.
图 6
图 6 不同粒径大小下目标区域内毗邻提升条颗粒的速率标准差沿SAG机内圆周位置的分布曲线图
Fig.6 Predicted SD profiles of speed of particles adjacent to lifter in target region along circumference of SAG mill under different particle sizes
在底脚区位置附近,颗粒会在提升条的作用下有一个与半自磨机转动同方向的角速度,模拟结果显示的确如此. 这一角速度在进入底脚区以后达到局部极大值,此后逐渐减小至几乎为0,且不同粒径对目标区域内颗粒的平均角速度几乎没有影响. 显然,相同角速度下,大颗粒具有更大的转动动能. 对临近衬板的底脚区附近颗粒的平均转动动能Er进行统计,结果如表2所列. 数据表明大颗粒(d=150 mm)的转动动能亦在小颗粒(d=30 mm)的100倍以上,这与颗粒的平动动能结果相似. 此外,颗粒的转动动能比对应平动动能小2个量级,认为转动对磨损的影响可以忽略.
3.4. 壁面分析
上文从颗粒运动角度分析了粒径对衬板磨损影响的原因. 基于分析结果可知,大颗粒造成提升条磨损更大的主要原因是其具有更大的动能. 但是,动能更大并不代表单次碰撞中碰撞力更大,或剧烈碰撞持续时间更长,或滑动强度更大. 本节的主要目的是从壁面角度分析粒径大小对提升条不同位置磨损的影响因素.
提升条上磨损最大的上平面以及右上角(观察图3可知)对应的瞬时磨损速率沿磨机内圆周分布如图7所示. 这里ΔW为Δt内提升条上4个区域各自的磨损体积增量,瞬时麿损率r=ΔW/(ΔtS). 首先关注一般情况下磨损最大的位置,即提升条的提升位置(位置4). 在提升位置处,相比于最大瞬时磨损率大小,粒径对最大值之后瞬时磨损率的降幅有更大的影响. 这与提升条的总瞬时磨损率结果一致,表明粒径更大时提升条经过底脚处后剧烈磨损持续的时间更长. 实际上,从4个位置的瞬时磨损率曲线均可观察到这一现象. 因此,粒径越大,目标区域颗粒运动越剧烈,这与图5中平均速率随粒径增大而增大的结果吻合. 与提升位置不同,粒径大小对上平面右侧(位置3)处的瞬时磨损率最大值有显著影响:随粒径增大,瞬时磨损率最大值逐渐增加,甚至粒径最大时(d=150 mm),平面右侧的最大瞬时磨损率超过了提升位置的最大值(见图7(e)). 图4显示,随粒径增大,整个提升条瞬时磨损率最大值增大. 由当前结果可知,主要原因是上平面右侧的最大瞬时磨损率随粒径增大而显著增大. 其余2个位置中,上平面左侧(位置1)的瞬时磨损率也值得注意. 随粒径增加,最大瞬时磨损率并未显著增加,但是曲线在最大值附近出现了一个平台,位置范围大约是135°~145°,这是如图3所示平面左侧与右上角磨损率差距并没有随粒径增大而增大的主要原因之一. 而这个平台的出现可能是因为大粒径颗粒造成的滑动强度更大.
图 7
图 7 提升条4个位置处瞬时磨损率在目标区域内沿SAG机内圆周分布曲线图
Fig.7 Predicted transient wear rates on four positions of lifters in target region along circumference of SAG mill
不同粒径大小下,提升条上不同区域所受平均切向应力τt沿磨机内圆周位置分布情况如图8所示. 同样,先关注提升位置(位置4)的情况. 显然,在所有粒径大小下,提升位置的切向应力相较于其他位置均更大. 与图7中对应的瞬时磨损率曲线相比较,可知在所有粒径下,当切向应力增长率明显趋缓时,对应瞬时磨损率达到最大值. 与之相比,其他位置(位置1、2、3)对应最大瞬时磨损速率均发生在快速增加阶段,且应力要显著小于提升位置应力. 因此,相比于提升条提升位置处的磨损,上表面磨损受颗粒滑动性质影响更大一些. 切向应力的以上特征在不同颗粒形状影响下同样可以观察到[24],具有一定普遍性. 有趣的是,不同粒径大小下,提升位置处所受切向应力在底脚区对应位置处大小差异并不明显,甚至大粒径(d=150 mm)造成的切向应力相对还要更小一些. 这表明壁面所受总力并不随粒径增大而增大. 由于粒径较大时颗粒与壁面间碰撞次数显著少于粒径较小时,对应单次碰撞的切向碰撞力
图 8
图 8 提升条4个位置处所受切向应力在目标区域内沿SAG机内圆周分布曲线图
Fig.8 Predicted tangential stress on four positions of lifters in target region along circumference of SAG mill
基于上述结果可知,改变粒径大小会显著影响底脚区处颗粒获得动能大小,最终使得壁面在单次碰撞中获得更多切向撞击能. 为了定量确定壁面与大颗粒碰撞时确实获得了更多动能,下文将从壁面角度进行能量分析. 如表3所示为不同粒径下衬板与颗粒碰撞后能耗率
表 3 衬板以及颗粒间碰撞的总能耗率
Tab.3
| d/mm | | | d/mm | | |
| 30 | 1.27 | 2.48 | 100 | 2.78 | 7.64 |
| 40 | 1.70 | 3.41 | 150 | 3.67 | 8.98 |
| 60 | 2.05 | 5.45 | − | − | − |
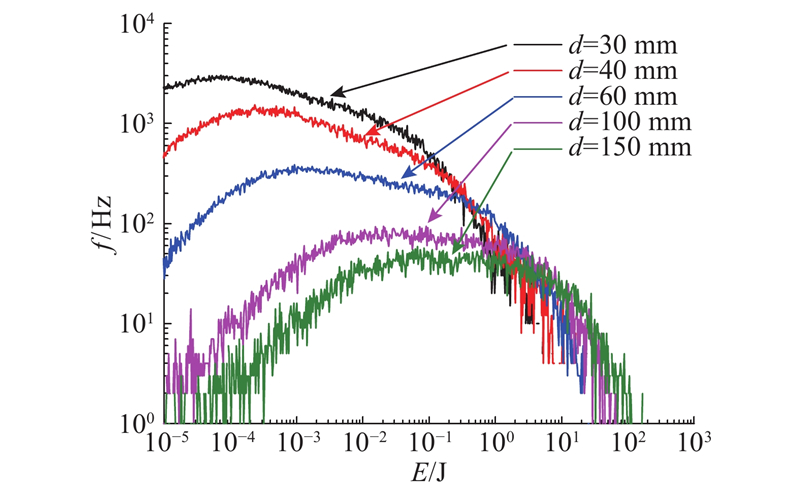
如图9所示为不同粒径下衬板与颗粒间碰撞的频谱图. 结果表明,当粒径较小时(d=30 mm),大量碰撞所在能级非常小(频率最大时对应10−5 J能级),且没有大于101 J能级的碰撞;而当粒径较大时(d=150 mm),频率最大时对应10−1 J能级且存在大量大于101 J能级的碰撞. 此外,小颗粒碰撞频率最大值量级为103 Hz,大颗粒对应的量级为101 Hz,与第2.3节中提到的小颗粒动能比大颗粒小2个量级对应.
图 9
图 9 颗粒与衬板的碰撞频谱图
Fig.9 Frequency spectrum of collisions between particles and liners
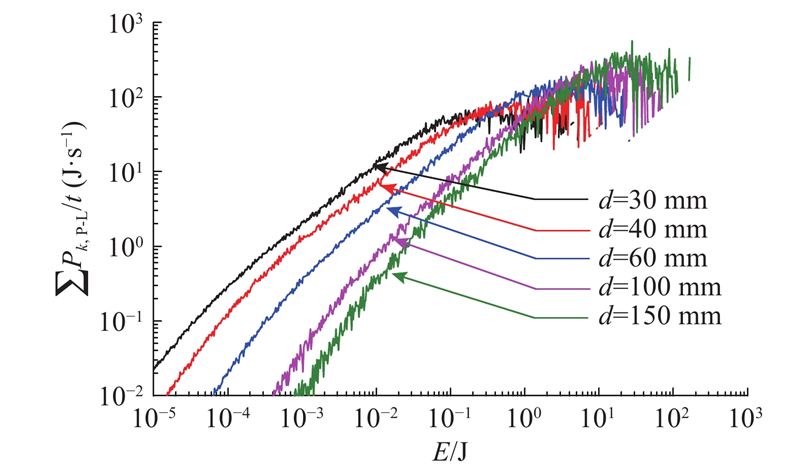
图 10
图 10 颗粒与衬板碰撞能耗谱图
Fig.10 Energy dissipation spectrum of collisions between particles and liners
4. 结 论
(1)随物料粒径增大,提升条所受总磨损逐渐增大(增速在粒径较小时尤为明显),但是粒径大小对提升条上磨损分布没有明显影响.
(2)不同粒径下,提升条上磨损均主要发生在其进入底脚区的过程中,且随粒径增大,不仅提升条的最大瞬时磨损率增大,剧烈磨损的持续时间也增加.
(3)粒径增大,磨损增加的主要原因如下:相比小颗粒,虽然大颗粒碰撞壁面次数少,但冲击壁面的能级更大,导致碰撞总能耗更大,且由于大颗粒改变运动状态需要更长时间,剧烈磨损的持续时间也更长.
(4)提升条上磨损最大的位置主要为上表面以及右上角处,但两者磨损受不同粒径颗粒影响的原因不同,上表面更多受不同粒径颗粒与壁面间的滑动性质影响,而右上角更多受底脚区不同粒径颗粒群推动难易程度的影响.
参考文献
颗粒射流冲击材料行为研究
[J].
Investigation of behaviour of particle impact on material by impinging jet
[J].
增压富氧燃煤锅炉省煤器管束磨损研究
[J].DOI:10.7652/xjtuxb201303010 [本文引用: 1]
Erosion of economizer tube bundles in pressurized oxy-fuel coal-fired boiler
[J].DOI:10.7652/xjtuxb201303010 [本文引用: 1]
Motion analysis of a tumbling ball mill based on non-linear optimization
[J].
Centrifugal mill charge motion and power draw: comparison of DEM predictions with experiment
[J].DOI:10.1016/S0301-7516(99)00063-0 [本文引用: 1]
振动平面上粒群运动的离散元模拟
[J].DOI:10.3321/j.issn:1000-1964.2006.05.005 [本文引用: 1]
Simulation of discrete element of particles motion on the vibration plane
[J].DOI:10.3321/j.issn:1000-1964.2006.05.005 [本文引用: 1]
离散元软件PFC在矿业工程中的应用现状及分析
[J].DOI:10.3969/j.issn.1005-7854.2011.01.019 [本文引用: 1]
Application status and analysis of discrete element software PFC in mining engineering
[J].DOI:10.3969/j.issn.1005-7854.2011.01.019 [本文引用: 1]
Discrete particle simulation of particulate systems: theoretical developments
[J].DOI:10.1016/j.ces.2006.12.089 [本文引用: 1]
Charge behaviour and power consumption in ball mills: sensitivity to mill operating conditions, liner geometry and charge composition
[J].DOI:10.1016/S0301-7516(01)00037-0 [本文引用: 2]
A review of computer simulation of tumbling mills by the discrete element method: Part II—Practical applications
[J].
Discrete element method (DEM) modelling of evolving mill liner profiles due to wear. Part II. Industrial case study
[J].DOI:10.1016/j.mineng.2005.02.010 [本文引用: 1]
Effect of liner design on performance of a HICOM® mill over the predicted liner life cycle
[J].DOI:10.1016/j.minpro.2014.11.003 [本文引用: 1]
DEM modelling of liner evolution and its influence on grinding rate in ball mills
[J].
立轴冲击破碎机加速板磨损仿真分析
[J].DOI:10.3969/j.issn.1001-3954.2017.06.010 [本文引用: 1]
Simulation and analysis on wear of accelerating board of vertical-shaft impact crusher
[J].DOI:10.3969/j.issn.1001-3954.2017.06.010 [本文引用: 1]
Erosion of surfaces by solid particles
[J].DOI:10.1016/0043-1648(60)90055-7 [本文引用: 2]
State-of-the-art review of erosion modeling in fluid/solids systems
[J].DOI:10.1016/S0360-1285(02)00022-9 [本文引用: 1]
CFD–DEM simulation of tube erosion in a fluidized bed
[J].DOI:10.1002/aic.15398 [本文引用: 1]
Numerical prediction of wear in SAG mills based on DEM simulations
[J].DOI:10.1016/j.powtec.2018.02.004 [本文引用: 5]
水平滚筒内二元颗粒体系径向分离模式的数值模拟研究
[J].DOI:10.3321/j.issn:1000-3290.2008.01.052 [本文引用: 1]
Numerical simulation of radial segregation patterns of binary granular systems in a rotating horizontal drum
[J].DOI:10.3321/j.issn:1000-3290.2008.01.052 [本文引用: 1]
Computational laboratory for discrete element geomechanics
[J].DOI:10.1061/(ASCE)0887-3801(1992)6:2(129) [本文引用: 1]
Erosion of metals by solid particles
[J].
3-D liner wear profile measurement and analysis in industrial SAG mills
[J].DOI:10.1016/j.mineng.2006.07.008 [本文引用: 2]
Influence of particle shape on liner wear in tumbling mills: a DEM study
[J].DOI:10.1016/j.powtec.2019.03.033 [本文引用: 1]