近年来,模块化多电平变流器[1-2]广泛应用于高压直流输电系统、电机驱动系统等中高压场合[3-7],其与传统电压源变流器相比,能降低运营成本和对环境的影响. 为了保证模块化多电平变流器(modular multilevel converter,MMC)的正常运行,如何实现模块电容电压均衡一直是研究热点. 目前最常用的电容电压均衡方法主要是排序算法[8-12]或在载波移相调制算法基础上设计各子模块电容电压闭环反馈控制对各子模块占空比进行微调,从而实现电容电压均衡[13]. 这些方法均须得到各模块电容电压,以2010年投入运行的美国Trans Bay Cable为例,该工程每个桥臂有216个子模块,其中16个为冗余模块,6个桥臂总共有1 296个模块,若采用电压传感器测量模块电容电压,工程复杂性较高,系统可靠性也较差.
为此,国内外学者研究状态观测器观测模块电容电压,包括全维观测器和降维观测器. Trabelsi等[14]设计了全维观测器利用测量与观测的桥臂电流之间的误差,结合各模块开关函数观测模块电容电压和桥臂电流,对观测器进行修正. 该观测器依赖于主电路参数,并且观测器稳定性证明存在问题,只证明了不同开关作用下的子系统稳定,而不能得到子模块一致渐近稳定的结论,另外子系统稳定也不能保证整个系统的稳定性,整个系统的稳定性还与开关作用的顺序等有关. 在此基础上,Nademi等 [15]设计了全维观测器,在观测模块电容电压和桥臂电流的同时,能够对模块容值进行观测,不过,所设计的模块容值自适应律只适用于同一桥臂容值相同的情况. Gregoire等[16]设计滑模降维观测器,测量各桥臂电流和桥臂模块总电压,利用测量的桥臂电压与观测值之间的误差对观测器进行修正,但该文献利用Lyapunov理论进行稳定性证明的结论是不完全的,得到的Lyapunov函数的导数是负半定的,因此只能证明观测误差是稳定的,而无法证明其一致渐近稳定,并且该条件只是充分条件,而非充分必要条件.
本研究设计了闭环降维状态观测器,只须测量6个桥臂电流和桥臂投入模块总电压,再结合实际系统开关函数即可观测各个模块的电容电压. 利用无源理论和持续充分激励条件进行稳定性分析,得到观测误差一致渐近稳定的充分必要条件. 基于该观测器提出MMC的系统控制策略. 在Matlab/Simulink中搭建工频为50 Hz条件下的21电平MMC仿真模型,仿真结果证实了该方法的有效性和相关结论的正确性.
1. MMC拓扑结构与建模
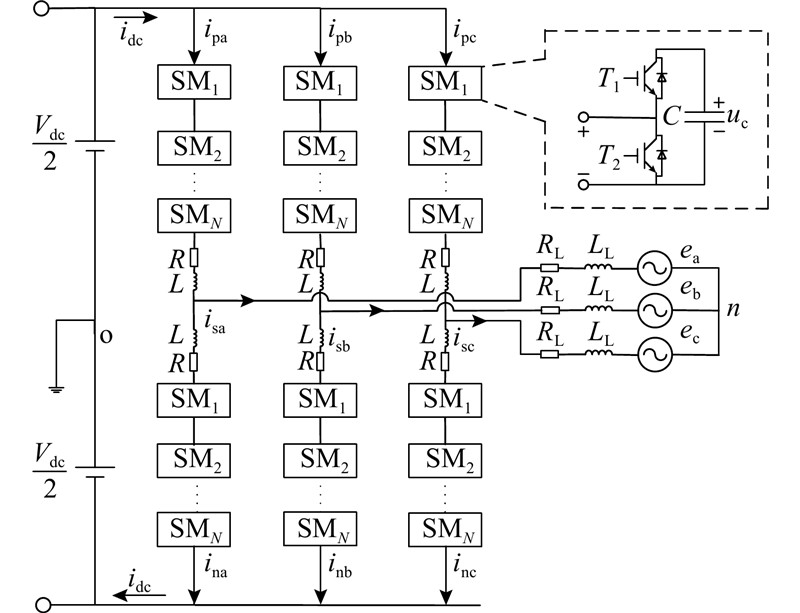
三相MMC拓扑结构如图1所示,图中,Vdc、idc为直流母线电压和电流;isj、ej、ipj、inj(j=a, b, c)分别为j相交流侧电流、电网电压、上桥臂电流和下桥臂电流;R、L分别为桥臂等效电阻和等效电感;RL、LL分别为交流侧等效电阻和等效电感;C为子模块电容;uc为子模块电容电压;SM为子模块;T1、T2为2个开关管;n为电网中性点. 三相MMC的每相有上下2个桥臂,共6个. 每个桥臂由N个结构相同的半桥子模块和1个桥臂电感级联组成. 子模块为功率单元,由2个绝缘栅门极晶体管(insulated gate bipolar transistor,IGBT)和1个电容组成,在同一时刻只有1个开关管导通,当开关管T1导通时模块处于接入状态,模块输出电压等于电容电压,当开关管T2导通时模块处于旁路状态,模块输出电压为0.
图 1
由MMC运行原理可知,子模块电容电压之间维持均衡对系统控制至关重要. 目前广泛采用的均衡策略如下:在确定导通模块数后,对单个桥臂模块的电容电压进行排序,同时检测桥臂电流方向;在充电时按电压从小到大投入子模块,在放电时按电压从大到小投入子模块. 电容电压均衡控制本质上是反馈控制,须安装电压传感器或设计观测器以实时得到各模块电容电压.
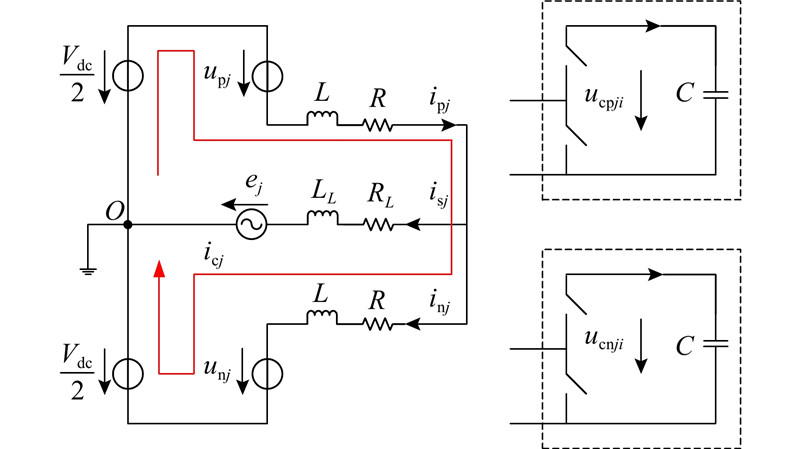
在正常运行时三相MMC的三相完全对称,在对MMC进行分析时可以只分析单相系统,当交流侧中性点接地时,MMC的j相(j=a、b、c)等效电路如图2所示. 在j相上、下桥臂投入的模块电压之和upj、unj可以由开关函数分别表示为
图 2
式中:Spji、Snji分别为j相上、下桥臂第i个子模块的开关函数,值为1表示子模块处于接入状态,值为0表示子模块处于旁路状态;ucpji、ucnji分别为j相上、下桥臂第i个子模块的电容电压.
第i个模块电容电压满足如下动态方程:
根据图2和基尔霍夫定律可以得到MMC的微分方程组:
式中:icj为j相环流,icj=(ipj+inj)/2.
将三相环流、三相交流电流以及6N个模块的电容电压作为系统状态变量x,即
系统外部激励为直流电压和三相电网电压,即
根据式(2)、(3)可以得到三相四线制MMC系统的状态空间模型为
式中:矩阵
其中,C为上下桥臂各模块容值.
2. MMC观测器设计
2.1. 状态观测器设计
在基于电容电压排序的均衡算法中,不仅须设置传感器测量6个桥臂电流以确定电容处于充电还是放电状态,还须测量6N个模块的电容电压以进行排序. 本研究所设计的观测器,只须设置12个传感器以测量6个桥臂电流和桥臂投入模块总电压即可观测所有模块的电容电压.
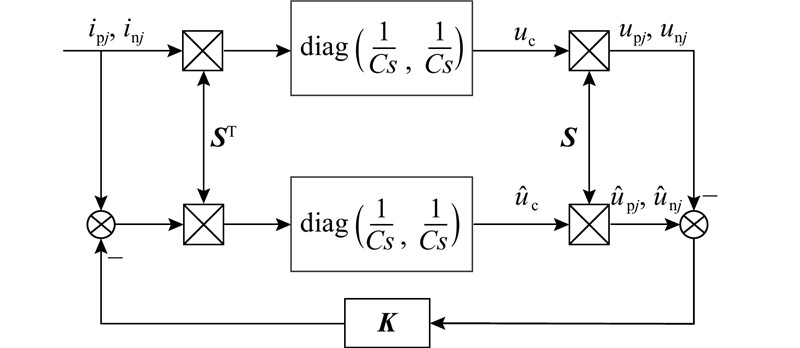
三相四线MMC系统的状态变量为三相交流电流、三相环流和6N个模块电容电压,为6N+6维系统. 若设计全维状态观测器,一方面这种观测器阶数较高,实现起来不方便,另一方面,6个桥臂电流均由电流传感器测量得到,已可以计算三相环流和交流电流,无须再进行观测. 因此本研究设计了维数为6N的降维观测器. 观测器结构如图3所示,上半部分表示被观测系统,下半部分表示观测器. 图中,ȗc为电容电压uc的观测值. 涉及了矩阵运算,具体含义如下:
图 3
式中:
2.2. 稳定性证明
初始条件不同例如模块电容初始电压不同会导致观测误差,须建立观测器误差模型来判断,当误差产生时电容电压观测值能否收敛到实际值. j相上、下桥臂第i个子模块的观测误差
由式(5)减去式(2),可以得到观测器子模块电容电压观测误差的微分方程:
设
式中:
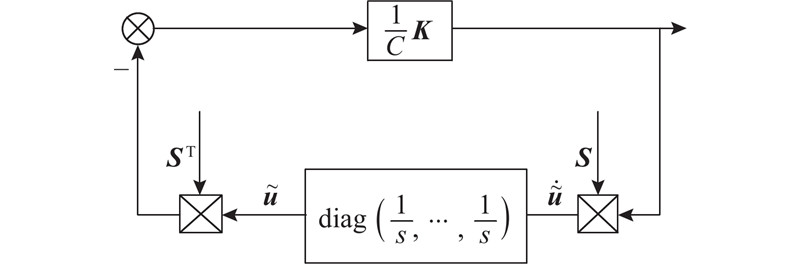
图 4)
图 4) MMC 电容电压观测误差反馈连接图
Fig.4 Feedback connection of observation error of capacitor voltages of MMC
总结来说,观测误差一致渐近稳定的充分必要条件为开关函数矩阵
根据式(10)、(11),可以得到
式(12)成立是观测误差一致渐近稳定的一个必要条件,通过对矩阵
对观测器的鲁棒性进行分析,当实际系统模块电容发生改变时,式(2)可以改写为
式中:
用式(5)减去式(13),得到电容存在偏差时的观测器误差方程表达式:
式中:
前文已证明在没有参数偏差时,观测误差系统是一致渐近稳定的. 根据文献[19]的引理4.6可知,以
3. 基于观测器的MMC系统控制
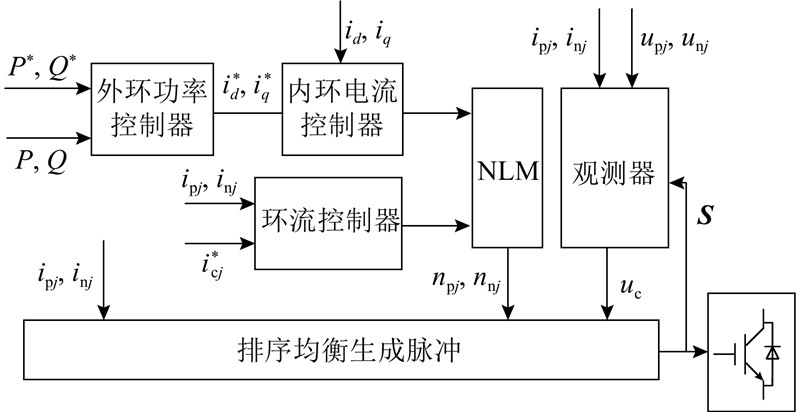
基于观测器的MMC系统控制策略如图5所示. 图中,P*、Q*分别为有功功率和无功功率给定值. MMC系统控制的实质是控制各相上、下桥臂导通模块数,即控制上、下桥臂电压由式(3)可知,通过控制上、下桥臂电压能够控制系统环流,通过控制上下桥臂电压差能够控制交流侧输出电流. 由此可以得到上、下桥臂的参考电压,并以此设计系统闭环控制器:
图 5
式中:
现对功率电流双闭环控制器进行说明,首先对三相交流电流isa、isb、isc作Park变换,将三相静止坐标系转换为两相旋转坐标系,得到id、iq. 控制器外环为功率环,给定交流有功功率和无功功率经实际有功功率和无功功率反馈后分别经过2个PI调节器后得到d、q轴电流给定
系统环流承担着MMC功率传输的任务,环流参考值可由交直流侧功率平衡关系得到:
式中:usj为j相交流侧输出电压. 式(16)得到的环流参考值是直流分量和交流二倍频分量的叠加. 由内模原理可知,PI调节器无法使系统环流准确跟踪参考值. 因此,参考值在经实际值反馈后,经过PIR调节器得到环流控制器输出usumj,PIR调节器的表达式如下:
式中:kp为比例增益;ki为积分增益;kr为谐振增益;ωr=2ω0为谐振频率,ω0为基波频率,取50 Hz;s为拉氏变换中的变量符号.
在经双闭环控制器得到udiffj、环流控制器得到usumj之后,结合式(15)可以得到各桥臂参考电压
式中:
在得到各桥臂导通模块数后,利用观测得到的模块电容电压以及测量得到的桥臂电流,基于排序均衡法决定投入的模块,产生控制开关管的脉冲信号.
4. 仿真分析
为了验证本研究所提方法的有效性,在Matlab/Simulink上按图搭建21电平MMC仿真模型,仿真电路参数如表1所示. 直流母线电压为4.0 kV,电网电压为2.3 kV,电网频率为50 Hz.
表 1 MMC基本参数表
Tab.1
| 变量 | 数值 | 变量 | 数值 | |
| C/μF | 4 000 | LL/mH | 2.01 | |
| L/mH | 0.265 4 | RL/Ω | 0.065 | |
| R/Ω | 0.03 | — | — |
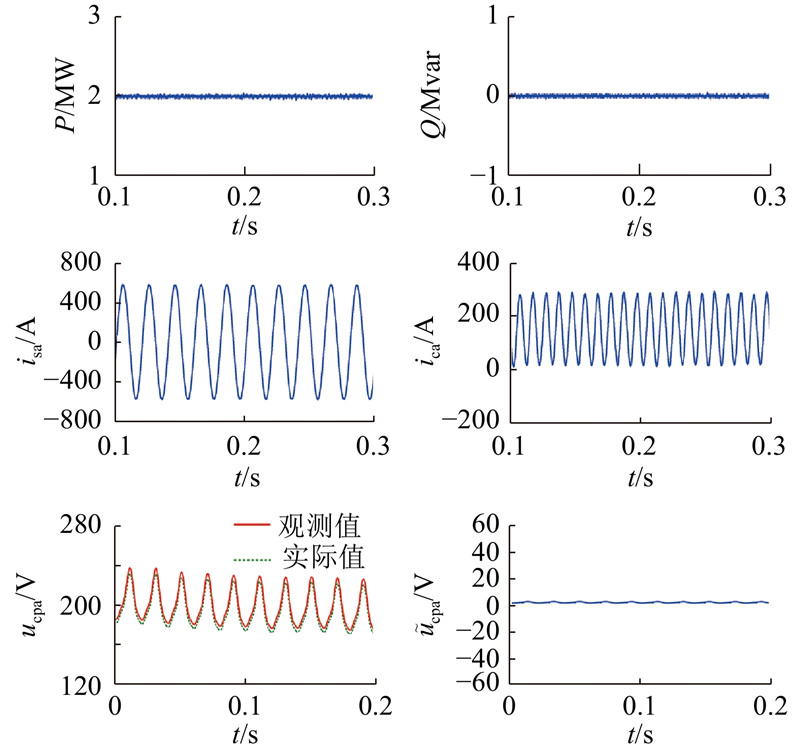
为了验证误差模型的收敛性,观察当观测器电容电压初始值和MMC实际值不同时,电容电压观测值能否跟踪上实际值. 实际模型给定有功功率为2 MW,无功功率为0 var. A相上桥臂前4个模块电容电压初始值分别为240、220、180、160 V,其余模块均为200 V;观测器所有模块电容电压初始值均为200 V. A相上桥臂前4个模块电容电压ucpa1、ucpa2、ucpa3、ucpa4观测值与实际值波形与观测误差
图 6
图 6 电容电压初值不同时MMC各变量波形
Fig.6 Variable waveforms of MMC with different initial capacitance voltages
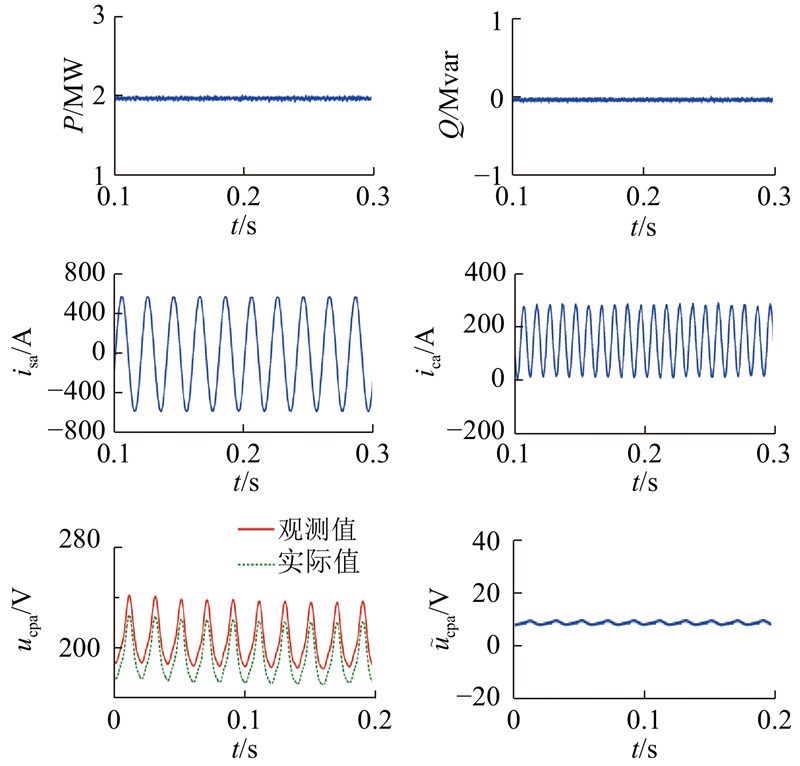
为了验证观测器的鲁棒性,当观测器模块电容值与实际值不同,而初始电容电压相同时,再次重复上述实验. 在MMC实际模型中,A相上桥臂前4个模块电容分别为6 000、5 000、3 000、2 000 μF,其余电容均为4 000 μF. 观测器的全部模块电容均为4 000 μF. 系统给定有功功率为2 MW,无功功率为0 var. A相上桥臂前4个模块电容电压观测值与实际值波形和误差波形如图7(a)所示,稳态时闭环系统各变量波形如图7(b)所示. 由图7(a)可知,电容电压观测值能较准确地跟踪实际值. 由于模块电容电压波动量与电容容值成反比,模块1、2实际容值大于观测器容值,因此电容电压波动量实际值应小于观测值;模块3、4实际容值小于观测值,因此电容电压波动量实际值应大于观测值,图8仿真结果符合理论分析. 由图7(b)可知,交流侧输出电流呈正弦变化,有功功率、无功功率和环流能够准确跟踪给定值. 说明在电容存在偏差的非理想情况下,该观测器仍能较准确地观测出模块电容电压,系统具有较强的鲁棒性.
图 7
图 8
图 8 电压测量存在误差时MMC各变量波形
Fig.8 Variable waveforms of MMC with voltage measurement errors
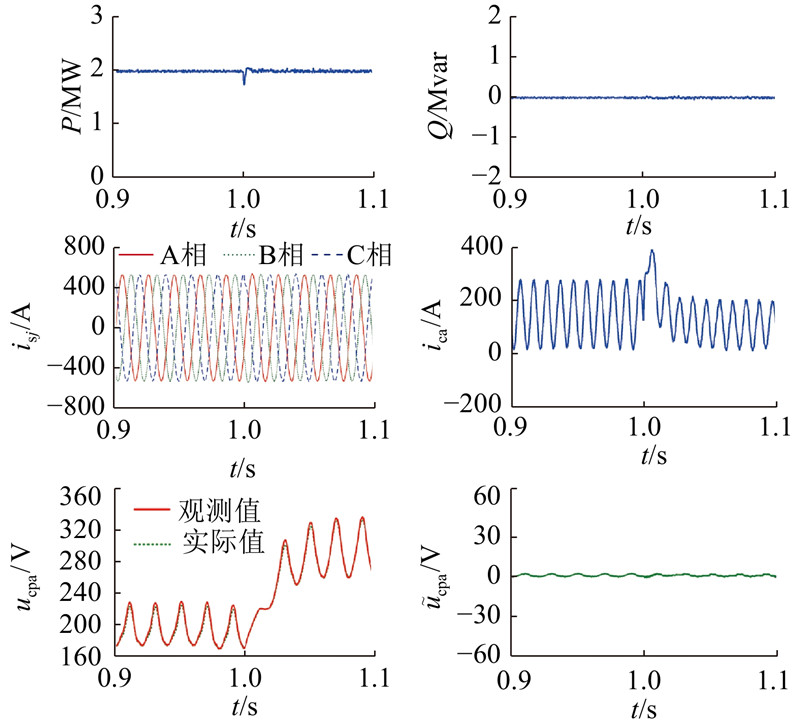
当电压传感器存在测量误差时,观测到的有功功率、无功功率、A相交流电流、A相环流、A相上桥臂平均电容电压ucpa观测值、实际值波形、观测误差
图 9
图 9 电流测量存在误差时MMC各变量波形
Fig.9 Variable waveforms of MMC with current measurement errors
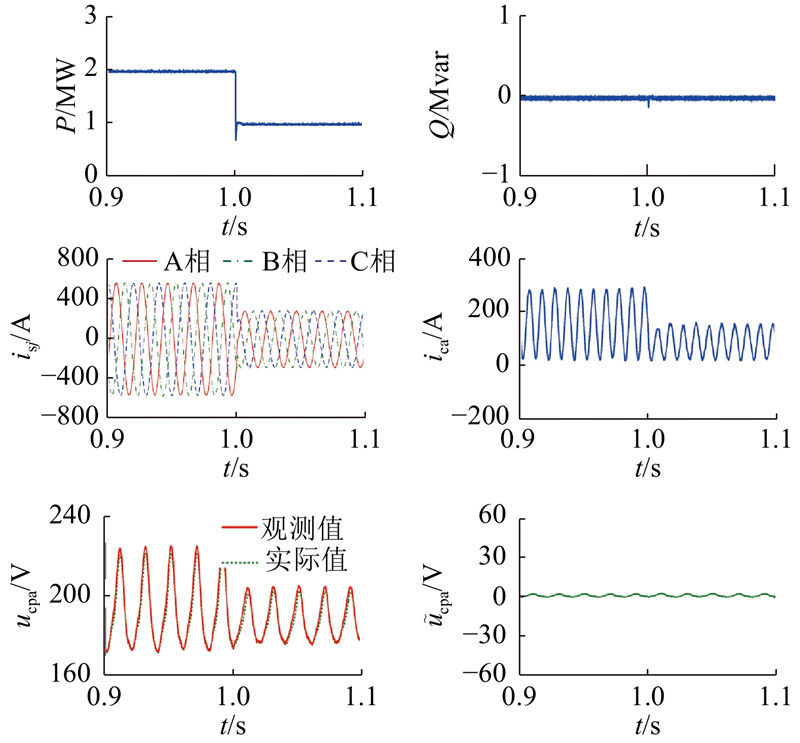
为了验证本研究观测器的动态性能,进行给定功率阶跃实验. 初始给定有功功率为2 MW,在t=1.0 s时变为1 MW. 给定无功功率始终为0 var. 闭环系统有功功率、无功功率、交流侧电流、A相环流、A相上桥臂20个模块电容平均电压的实际值、观测值和误差波形如图10所示. 在稳态时,系统功率波形、电流波形能准确跟踪给定值,观测器电容电压能准确跟踪实际电容电压,稳态时的误差不超过2.5 V. 当给定有功功率发生阶跃变化时,系统有功功率迅速变化到新的给定值,无功功率稳定在0 var.功率减小为原值的1/2,而电网电压和直流母线电压未发生变化,因此交流电流幅值、环流的直流分量和二倍频分量、电容电压波动量均减小为原值的1/2,符合理论值,整个过程观测器电容电压始终能够跟踪实际电容电压,观测器观测误差最大值未发生变化.
图 10
图 10 功率阶跃变化时MMC各变量波形
Fig.10 Variable waveforms of MMC with step change of power
为了进一步验证系统的动态性能,进行直流母线电压阶跃实验. 给定有功功率为2 MW,无功功率为0 var. 在t=1.0 s时,直流母线电压由4 000 V阶跃变化到6 000 V,系统仿真波形如图11所示. 可以看出,由于给定功率未发生变化,系统有功功率、无功功率保持稳定. 由于电网电压未发生变化,交流电流幅值保持不变. 环流的直流分量和二倍频分量幅值减小到原值的2/3,电容电压平均值由200 V增大到300 V,波动量也随直流电压的增大而增大,符合理论分析. 整个过程电容电压观测值始终准确跟踪实际值,说明观测器和系统具有较好的动态性能.
图 11
图 11 直流电压阶跃变化时MMC各变量波形
Fig.11 Variable waveforms of MMC with step change of direct current voltage
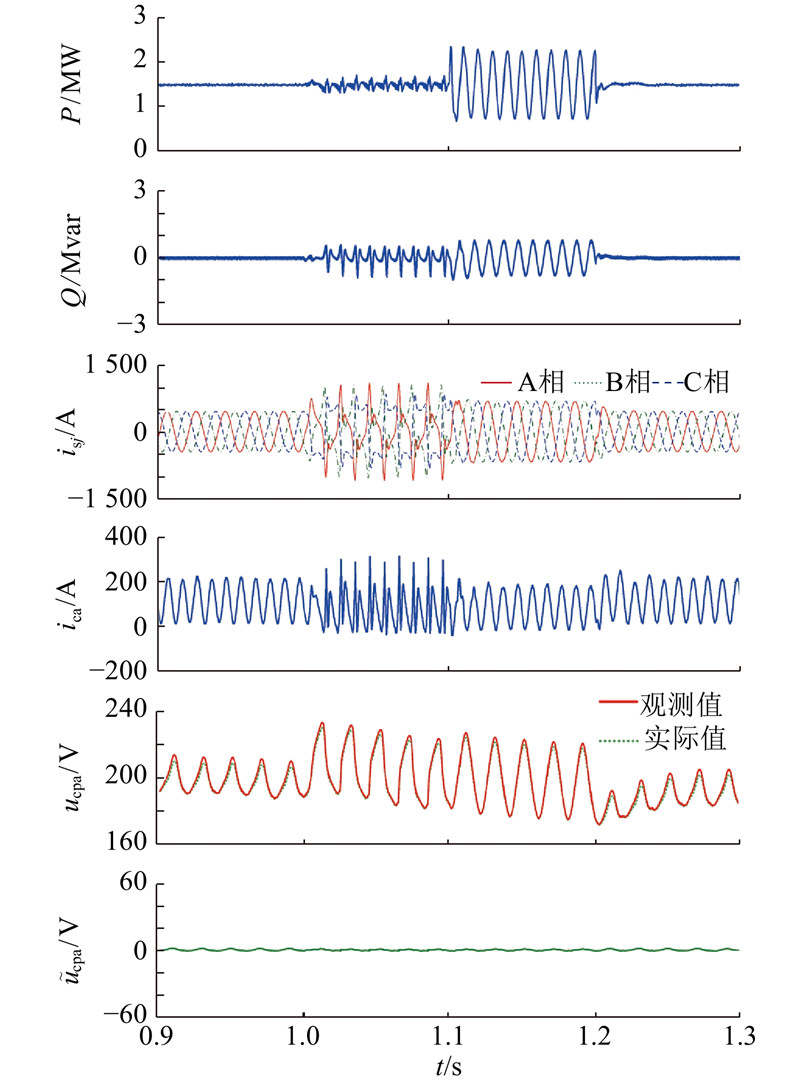
现验证观测器在发生故障时能否运行,初始三相电网平衡,给定有功功率为1.5 MW,无功功率为0 var. 在t=1.0 s时发生电网不平衡故障,A、B相电压幅值变为原值的一半. 在电网发生不平衡故障时,若仍使用电网平衡时的系统闭环控制策略,功率将发生二倍频波动,交流电流出现大量负序分量,此时应采取措施抑制交流电流的负序分量,但同时会增大功率的二倍频波动. 电网不平衡时的系统控制策略非本研究研究内容,在此不再赘述,可参考相关文献[20]. 在t=1.1 s时系统采取抑制交流电流负序分量的控制策略,在t=1.2 s时故障清除,电网恢复平衡状态,整个过程观测器结构无须改变. 系统有功功率、无功功率、交流侧电流、A相环流、A相上桥臂20个模块电容平均电压的实际值、观测值和误差波形如图12所示. 在t=1.0 s发生电网不平衡故障时,功率波动量增大,交流电流和环流出现畸变,在t=1.1 s采取电网不平衡控制策略时,功率二倍频波动进一步增大,交流电流和环流畸变程度降低,在t=1.2 s故障清除后各波形恢复正常,整个过程电容电压观测值始终准确跟踪实际值,说明该观测器具有较好的故障穿越能力.
图 12
5. 结 语
本研究运用无源理论和持续充分激励条件证明了所设计的MMC模块电容电压观测器的一致渐近稳定性,对容值偏差和传感器测量误差等具有一定的鲁棒性,这一结论能够在很大程度上降低算法设计、实现以及维护的复杂性. 另外,本研究基于观测器设计的反馈控制器,能够实现整个闭环系统的稳定运行,具有较好的动态性能和故障穿越能力,在高压直流输电等工程中有较好的应用价值. 在MATLAB/Simulink中搭建的21电平MMC仿真模型证实了本研究所提理论的正确性.
对于本研究所提出的观测器,当其误差模型一致渐近稳定时,开关函数须满足持续充分激励条件。当采用载波移相调制策略和最近电平调制策略时,开关函数满足该条件。当采用其他调制策略时,开关函数是否满足该条件,还须进一步研究。
参考文献
Medium-voltage multilevel converters-state of the art, challenges, and requirements in industrial applications
[J].DOI:10.1109/TIE.2010.2049719 [本文引用: 1]
Medium-voltage vector control induction motor drive at zero frequency using modular multilevel converter
[J].
New efficient submodule for a modular multilevel converter in multiterminal HVDC networks
[J].
Internal balance during low-voltage-ride-through of the modular multilevel converter statcom
[J].
Integrated BMS-MMC balancing technique highlighted by a novel space-vector based approach for BEVs application
[J].
Small-scale modular multilevel converter for multi-terminal DC networks applications: system control validation
[J].
模块化多电平换流器改进最近电平调制策略
[J].
Improved nearest level modulation strategy for modular multilevel converters
[J].
采用质因子分解法的模块化多电平换流器电容电压平衡优化算法
[J].
An optimized capacitor voltage balancing control algorithm for modular multilevel converter employing prime factorization method
[J].
一种适用于高电压等级的MMC子模块均压算法
[J].DOI:10.11930/j.issn.1004-9649.2016.02.118.04
A high voltage level MMC sub module equalization algorithm
[J].DOI:10.11930/j.issn.1004-9649.2016.02.118.04
模块化多电平变流器的直流电压控制方法
[J].
DC voltage control method of module multilevel converter
[J].
模块化多电平换流器子模块平均开关频率的精确控制方法
[J].DOI:10.7500/AEPS20160124001 [本文引用: 1]
Precison control method of average sub-module switching frequency for modular multilevel converters
[J].DOI:10.7500/AEPS20160124001 [本文引用: 1]
采用载波移相调制的模块化多电平换流器电容电压平衡控制
[J].
Capacitor voltage balancing control by using carrier phase-shift modulation of modular multilevel converters
[J].
Modular multilevel converter with an adaptive observer of capacitor voltages
[J].DOI:10.1109/TPEL.2014.2301879 [本文引用: 1]
On the Stability of nonautonomous differential equations ẋ = A + B(t)x, with skew symmetric matrix B(t)
[J].
Investigation of MMC-HVDC operating region by circulating current control under grid imbalances
[J].DOI:10.1016/j.jpgr.2017.07.003 [本文引用: 1]