现有的不等圆Packing问题求解方法大致可以分为2类:全装填方法、定序定位方法. 全装填法用容器内的物理格局描述Packing解,并在容器内移动圆形物体,其搜索的是整个布局. 定位定序法用圆形物体之间的序列描述Packing解,并用放置规则构造Packing解,其搜索的是放置序列. 全装填方法将所有圆形物体强行装入容器,然后不断调整各圆形物体的位置,直到所有物体都满足放置约束,进而找到Packing解. 该方法允许圆形物体之间、圆形物体与容器之间存在干涉,从而使得解空间变得光滑连续(转化为干涉量最小化问题),可以采用一些优化方法进行求解,比如拟物拟人法[5-6],空间搜索法[7-8]、势能曲面扁平法[9-10]、迭代禁忌法[11-12]等. 全装填方法一般通过缩小容器半径逐渐逼近最优解,其缺点是不能保证得到的解是可行解,难点是如何对当前格局加以变换以生成更有前景的新格局. 定序定位法将所有圆形物体排序,然后逐个放到根据放置规则确定的位置上. 当最后1个圆形物体的位置确定时,就得到1个Packing解. 解的质量取决于放置规则和放置序列. 对放置规则的设计和放置序列的优化可以形成不同的求解方法,比如占角算法[13]、最大穴度法[14]、集束搜索法[15-16]、局部搜索法[17]、混合算法[18]等. 给定1个放置序列,通过定序定位能快速得到1个Packing解,并保证是可行解. 该方法的缺点是,在将无限解空间缩小到离散解集时可能会移除全局最优解和一些好的局部最优解,难点是设计恰当的放置规则和回溯判断准则.
从任何物体都占据一定空间的角度来看,不等圆Packing问题的解就是不同圆形物体在容器内占据着不同空间. 当圆形物体所占空间发生变化时,就会形成新的Packing解. 因此,不等圆Packing问题可以抽象为空间分配问题(即将容器空间合理有效地分配给给定的圆形物体),进而采用分配的方法进行求解.
不等圆Packing问题可以被抽象为空间分配问题,群智能劳动分工本质上属于任务分配. 针对不等圆Packing问题,本研究借鉴任务分配来实现空间分配,根据刺激-响应原理提出新的群智能劳动分工方法(swarm intelligence labor division algorithm,SILDA). 该方法包含动作、刺激和阈值,动作的设计结合了不等圆Packing问题的特点,刺激的设计融入了对无前景搜索区域的逃离,阈值的设计考虑了对动作失败的惩罚. 最后,通过实验对所提方法的有效性进行检验.
1. 空间分配视角下的不等圆Packing问题分析
1.1. 问题描述
图 1
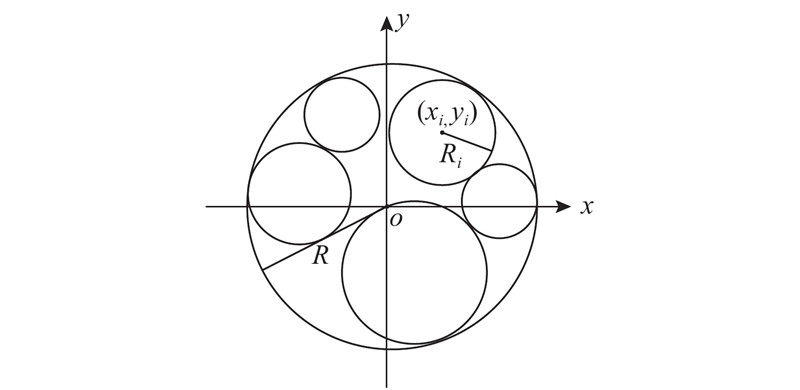
图 1 不等圆Packing问题简化图
Fig.1 Simplified schematic of unequal circle packing problem
将满足不重叠约束条件的布局称为合法解,否则称为非法解. 在搜索过程中,非法解普遍存在. 为了度量布局X的优劣程度,根据拟物法定义其势能函数[5]:
式中:
U(X)越小,格局X的质量越高. 当且仅当U(X)=0时,X为合法格局. 在实际计算中,由于计算精度的限制,一般约定在总体势能小于10−20时停机.
1.2. 空间分配特性分析
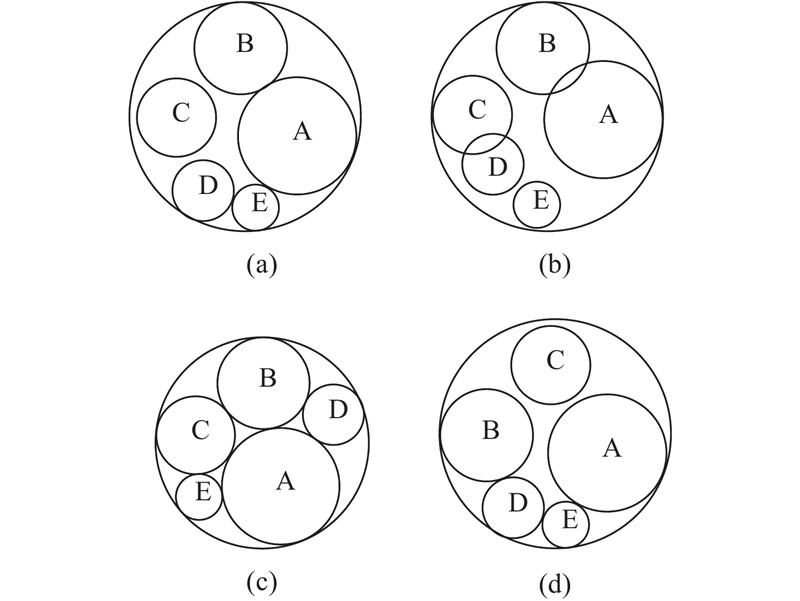
材料和空间具有二元性,即材料和其所占空间在一定情况下可以等效. 对不等圆Packing问题而言,将一组圆饼装入容器的结果就是圆饼在容器内占据着不同的空间. 因此,不等圆Packing问题可以等效为空间分配问题,即将容器空间合理地分配给各圆饼,以达到容器空间利用率最大或浪费最小的目的. 结合空间分配格局示例(见图2),总结不等圆Packing问题的空间分配特性如下:
图 2
1)每个空间分配格局都对应不等圆Packing问题的1个布局解. 将容器空间分配给所有的圆饼,形成1个空间分配格局. 当分配给圆饼的空间发生变化时,就形成新的空间分配格局. 如图2所示,4个不同的空间分配格局对应4个布局解. 2)容器空间的占据情况决定布局解是否合法. 当容器内所有空间最多只被1个圆饼占据时,对应的布局解合法,如图2(a)所示. 当容器内的某一空间同时被2个或2个以上的圆饼占据时,对应的布局解不合法,如图2(b)所示. 3)空间分配格局的质量可用容器空间利用率来衡量. 容器空间利用率是圆饼所占空间与整个容器空间的比值,这也是不等圆Packing问题中常用的评价指标. 对比图2(a)、(c),后者的容器空间利用率更高,即其对应的布局解更好. 4)对圆饼执行一系列动作(比如固定、平移、交换、跳跃等)可以实现任意2个空间分配格局之间的转换. 比如,交换图2(a)中的圆饼B、C可以得到图2(d). 更进一步地,在圆饼之间恰当地协调这些动作,可以实现容器空间更有效的分配.
2. 求解不等圆Packing问题的群智能劳动分工方法
2.1. 群智能劳动分工中的刺激-响应原理
在社会性昆虫中,不同的个体执行不同的任务,这种现象即为劳动分工[19]. 劳动分工中的智能体现在自组织和适应性2个方面. 自组织指个体在无中心控制和无全局信息的情况下,仅依靠局部信息进行简单交互就能实现有效的任务分配. 适应性指执行各项任务的个体比例在外部变化和内部扰动下是可以变化的,且该比例下个体的分工恰好符合族群对各项任务的要求.
群智能劳动分工中的刺激-响应原理简要描述如下[23]:每个任务都有1个刺激与之对应,刺激强度与任务的紧急程度有关. 个体对于每个任务都存在1个响应阈值,阈值大小反映个体执行任务的实际差别. 当任务的刺激强度超过个体的响应阈值时,个体执行任务的概率高;反之,个体执行任务的概率低. 刺激越强,执行任务的个体越多.
Bonabeau等[24-25]给出刺激-响应原理的量化形式:个体执行任务的概率
2.2. 任务分配和空间分配的比较
为了利用群智能劳动分工求解不等圆Packing问题,从分配的视角对两者进行对比,如表1所示. 可以看出,群智能劳动分工属于任务分配,不等圆Packing问题属于空间分配,两者都作为分配问题为本研究所提方法提供了可能. 同时,群智能劳动分工的适应性特点恰好满足不等圆Packing问题对求解方法的普适性要求,进一步增强了本研究所提方法的可行性.
表 1 群智能劳动分工和不等圆Packing问题之间的比较
Tab.1
| 性质 | 群智能劳动分工 | 不等圆Packing问题 | |
| 分配类型 | 不同的个体执行族群中不同的任务,属于任务分配 | 不同的圆饼占据容器内不同的空间,属于空间分配 | |
| 离散型 | 族群任务由一系列离散任务组成,个体执行的是任务集合中某个离散的元素,属于离散分配 | 容器空间是连续的整体,圆饼在容器内所占据的空间是可以连续变化的,属于连续分配 | |
| 适应性 | 群智能劳动分工具有适应性,即在动态环境下始终能够实现有效的任务分配 | 不等圆Packing问题要求算法具有普适性,即对所有算例均表现出较好的求解性能 |
由表1还可以看出,群智能劳动分工属于离散分配,不等圆Packing问题属于连续分配,因此,须对连续分配进行离散化处理. 在不等圆Packing问题的求解过程中,一般会对圆饼执行交换、跳跃、平移、固定等动作,从而调整圆饼在容器内的位置. 对圆饼而言,不同的动作通常对应容器内不同的空间,在理论上,通过执行这些动作,圆饼可以到达容器内的任意空间处. 从而,空间分配由圆饼占据连续变化的空间简化为圆饼执行这些离散的动作. 在不等圆Packing问题的求解过程中,通常会对圆饼执行平移、交换、固定、跳跃等动作. 通过执行这些动作,圆饼可调整其在容器内占据的子空间. 对不等圆Packing问题而言,实现空间分配的方式之一就是圆饼执行这些不同的动作.
2.3. 群智能劳动分工方法
在群智能劳动分工中,个体执行觅食、防御等任务完成任务分配. 在不等圆Packing问题中,圆饼执行交换、跳跃等动作完成空间分配. 将圆饼看成蚂蚁,动作看成任务,基于刺激-响应原理,提出面向不等圆Packing问题的群智能劳动分工方法.
2.3.1. 动作
对圆饼而言,不等圆Packing问题就是寻找圆饼在容器内的最佳排放位置. 在此过程中,一般会对圆饼执行固定、平移、交换、跳跃等动作. 在固定动作下,圆饼的位置保持不变. 在平移、交换、跳跃等动作下,圆饼的位置发生变化. 实验发现,当容器半径较大时,整个布局较宽松,平移、交换、跳跃等动作都能有效降低整体势能;当容器半径较小时,整个布局较紧凑,交换比平移和跳跃能更好地改善格局(尤其对半径较大的圆饼更为明显). 此外,实际布局经验也表明[26],在手工布局时经常不断交换两物体的位置,以使资源的利用趋于合理化. 因此,本研究仅考虑交换和固定2种动作.
交换动作在本质上是对格局进行变换,在变换时要兼顾继承性和改进性,既不能严重破坏当前已找到的较优格局,又要得到更有前景的格局. 一般而言,交换大小相似的圆饼能有效改进当前格局,交换位置邻近的圆饼不会严重破坏当前格局. 根据相似原则和邻近原则,定义2种交换动作:1)将所有圆饼按半径从大到小排序,交换半径不等且序号之差不大于3的2个圆饼;2)交换圆心距离小于半径之和的1.8倍的2个圆饼. 一旦圆饼执行交换动作,这2个动作皆有1/2的概率被选中. 假设当前布局为
2.3.2. 刺激
在刺激-响应原理中,刺激描述了个体执行任务的外部驱动力. 刺激越大,任务越紧迫. 在拟物策略下,不等圆Packing问题转化为弹性势能最小化问题. 当整个布局的弹性势能较小时,说明大部分圆饼已经找到了合适的位置. 此时,固定动作发出的刺激大,而交换动作发出的刺激小. 当整个布局的弹性势能较大时,说明大部分圆饼之间存在干涉. 此时,交换动作发出的刺激大,固定动作发出的刺激小. 因此,固定动作的刺激与整个布局的弹性势能成负相关,交换动作的刺激与整个布局的弹性势能成正相关.
假设固定动作的刺激与整个布局的弹性势能成反比,交换动作的刺激与整个布局的弹性势能成正比,则固定动作、交换动作的刺激的表达式分别为
式中:
对于格局X,圆饼执行交换动作后得到其邻域格局X′,执行固定动作后格局保持不变. 不等圆Packing问题具有维数高、局部极值点多等特点. 为了不在无前景区域的局部极小点附近花费过多时间,同时又不轻易错过有前景的搜索区域,对交换动作的刺激进行衰减. 具体而言,将所有圆饼依次执行1次动作称为1个周期,用p对周期进行计数,
式中:d为衰减系数.
当U>10−5时,认为解空间中该点附近的区域为无前景区域,d=0.75. 当U<10−5时,认为解空间中该点附近的区域为有前景区域,d=0.95.
2.3.3. 阈值
在刺激-响应原理中,阈值反映个体执行任务的内部倾向性. 阈值越小,倾向性越强. 在拟物策略下,不等圆Packing问题中圆饼位置的优劣可用其弹性势能来度量. 当圆饼找到好位置时,其对应的弹性势能较小. 此时,圆饼执行固定动作的倾向性大,执行交换动作的倾向性小. 当圆饼未找到好位置时,其对应的弹性势能较大. 此时,圆饼执行交换动作的倾向性大,执行固定动作的倾向性小. 因此,圆饼对应固定动作的阈值与其弹性势能成正相关,对应交换动作的阈值与其弹性势能成负相关.
假设圆饼i对应固定动作的阈值
式中:
在圆饼成功执行交换动作后,新的布局会代替旧的布局,刺激和阈值会在新布局的基础上被重新定义. 若在圆饼执行交换动作后,新布局没有旧布局好,说明该交换动作失败. 此时,对阈值进行一定的惩罚,惩罚的意义在于使得该圆饼下次执行交换动作的概率降低. 具体来说,在圆饼i执行交换动作失败后,阈值更新方式如下:
式中:U′/U为惩罚系数,U′为执行交换动作后新格局的势能,U为执行交换动作前旧格局的势能.
2.3.4. 执行概率
根据刺激-响应原理,圆饼执行动作的概率由动作刺激和圆饼阈值共同决定. 刺激越大,概率越大;阈值越小,概率越大.
圆饼i执行固定动作、交换动作的概率分别为
2.3.5. 跳坑策略
不等圆Packing问题在求解过程中易陷入局部极小值陷阱,设计快速有效的跳坑策略是研究者的关注点之一. 跳坑策略有2个关键点:一是搜索到局部极小值;二是不完全破坏局部极小值的布局结构. 基于此,本研究设计如下跳坑策略. 若所有圆饼在连续4个周期内都执行固定动作,则认为该格局是局部极小值点. 计算当前局部极小值格局中所有圆饼的相对弹性势能(即势能半径比Ui/Ri),按照相对弹性势能由大到小对圆饼进行排序,选择前
2.3.6. 算法流程
基于上述描述,群智能劳动分工方法的算法流程如下:
1. 初始化:随机生成格局X,容器半径R=2.4(R1 2+R2 2+…+RN 2)1/2,
αβ=108,k=0,p=0,improve=0,jump=0,JT=0;
2. 计算初始格局X的弹性势能U,每个圆饼的相对弹性势能Ui/Ri;
3. while JT<10do
4. if U>10−5 then
5. d=0.75;//设置刺激衰减系数
6. else
7. d=0.95;//设置刺激衰减系数
8. end if
9. 将圆饼按照相对弹性势能由大到小排序得到序列L;
10. for序列L中的每一个圆饼 do
11. 根据式(9)、(10)计算圆饼执行固定和交换的概率Γi,f和Γi,s;
12. 在(0,1)内生成一个随机数r;
13. if r<Γi,s/(Γi,s+Γi,f)then
14. k=0,圆饼执行交换动作,得到布局X′;
15. if U′<U then
16. X=X′,U=U′,improve=1,p=0,JT=0; //更新当前格局
17. if U<10−20 then//保存(R,X);
18. R=0.99R,k=0,p=0,improve=0,jump=0;//缩小半径;
19. end if
20. 计算格局X中每个圆饼的相对弹性势能Ui/Ri,转4;
21. else
22. improve=0,根据式(8)更新阈值;//格局保持不变
23. end if
24. else
25. k=k+1,improve=0,圆饼执行固定动作;//格局保持不变
26. end if
27. end for
28. if k=N then//所有圆饼在1个周期内都执行固定动作
29. jump=jump+1,k=0;
30. else
31. jump=0,k=0;
32. end if
33. if jump=4 then//所有圆饼在连续4个周期内都执行固定动作
34. jump=0,JT=JT+1,执行跳坑策略,更新布局X;
35. 计算格局X中每个圆饼的相对弹性势能Ui/Ri,转4;
36. end if
37. if improve=0 then
38. p=p+1,根据式(5)更新刺激,转10;
39. end if
40. end while
41. return(R,X)
3. 实验结果与分析
为了检验SILDA的性能,采用Java语言实现SILDA,并在个人计算机上进行计算实验(2.40 GHz CPU×4,4 GB内存). 选取2组共20个算例作为测试集,以圆形容器半径作为主要评价指标,以计算时间为次要评价指标,进行对比分析. 对于每个算例,独立运行SILDA 20次,记录其中最小的容器半径Rmin和平均运行时间t.
第1个测试集以工程中的实际要求为背景,共包含6个算例,其中圆饼的个数分别为20、40、15、30、30、25,具体数据见文献[4]. 张维等[4]描述了2种算法:遗传模拟退火算法(genetic simulated annealing,GSA)、改进遗传模拟退火算法(improved genetic simulated annealing,IGSA),均以式(1)作为问题模型. GSA的基本原理是利用遗传算法产生新解,然后利用模拟退火算法决定是否接受新解. IGSA在GSA的基础上引入最优个体保留策略,对交叉概率和变异概率进行自适应调整,在退火操作中增加随机扰动环节. 如表2所示为SILDA与GSA[4]、IGSA[4]在第1个测试集上的结果比较,每个算例的最小容器半径以粗体表示. 可以看出,对于最小容器半径,SILDA在所有算例上均取得了最好的结果. 圆形容器的半径越小,容器的面积利用率Ra越高. 文献[4]也将面积利用率作为测试指标,IGSA 得到的平均面积利用率为73.61%,SILDA得到的平均面积利用率为80.37%. 文献[4]未给出IGSA的计算时间,SILDA在大多数算例上的计算时间不到1 s. 如图3所示为SILDA在第1个测试集上的布局结果图.
表 2 第1组算例的实验结果比较
Tab.2
| 算例 | GSA[4] | IGSA[4] | SILDA | |||||
| Rmin | Ra/% | Rmin | Ra/% | Rmin | Ra/% | |||
| 1 | 9.872 5 | 51.30 | 8.312 1 | 72.37 | 7.886 9 | 80.38 | ||
| 2 | 13.918 5 | 51.62 | 11.499 0 | 75.63 | 11.035 7 | 82.11 | ||
| 3 | 9.116 1 | 54.15 | 7.813 7 | 73.71 | 7.680 9 | 76.28 | ||
| 4 | 13.681 7 | 48.08 | 11.190 6 | 71.87 | 10.623 6 | 79.74 | ||
| 5 | 10.685 4 | 52.55 | 8.960 6 | 74.73 | 8.610 7 | 80.92 | ||
| 6 | 11.425 8 | 49.79 | 9.413 2 | 73.36 | 8.861 8 | 82.77 | ||
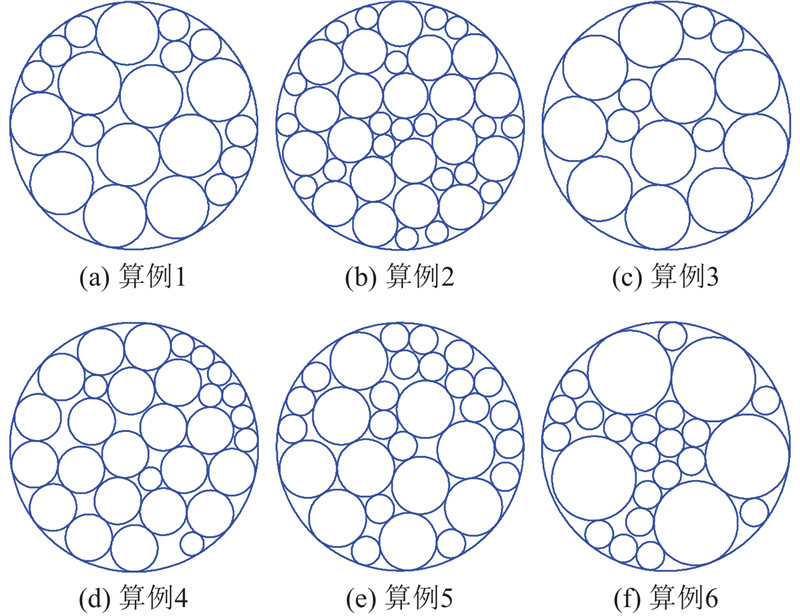
图 3
图 3 SILDA在第1个测试集上的布局结果图
Fig.3 Packing layouts found by SILDA on first set of instances
第2个测试集是常用的基准测试集之一,共包含14个算例,其中圆饼的个数分别为5、6、7、8、9、10、12、14、16、18、20、25、30、35,具体数据见文献[1]. 如表3所示为SILDA与排样分区禁忌搜索算法(tabu search with nested partitioning,TS/NP)[18]、带全局变换禁忌搜索算法(tabu search with global perturbation,GP-TS) [1]、拟物型邻域搜索算法(quasi-physical method with neighborhood search,QP-NS) [6]、变邻域下降迭代禁忌搜索算法(iterated tabu search with variable neighborhood descent,ITS-VND) [12]在第2个测试集上的结果比较,每个算例的最小容器半径以粗体表示,次小容器半径以下划线标出. 前7个算例的圆饼个数较少,相关文献报道的结果往往是全局最优解,SILDA也得到了一样的结果,所以最优解未用黑体表示. 须说明的是,SILDA在前7个算例上所得的容器半径比QP-NS所得的大10−4,这是因为SILDA所得格局严格无嵌入,而QP-NS允许所得格局有一定的嵌入. 事实上,两者所得格局的结构是一样的. 以算例CST10-1为例(本研究中图4(a)与文献[6]中图3(a)),各圆饼在容器内的相对位置是一致的. 因此,认为SILDA与QP-NS在前7个算例上得到的解是一样的. ITS-VND是目前已知的最小容器半径的记录保持者. 由表3可以看出,对于最小容器半径,SILDA在前7个算例上与ITS-VND持平,在后7个算例上仅次于ITS-VND. 对于计算时间,ITS-VND的平均运行时间为100 000 s,远大于SILDA的运行时间. 如图4所示为SILDA在算例CST10-1、CST20-1和CST30-1上的布局结果图.
表 3 第2组算例的实验结果比较
Tab.3
| 算例 | TS/NP[18] | GP-TS[1] | QP-NS[6] | ITS-VND[12] | SILDA | |||||||||
| Rmin | t/s | Rmin | t/s | Rmin | t/s | Rmin | t/s | Rmin | t/s | |||||
| CST5-1 | 1.751 552 | 1 270 | 1.751 600 | 1 | 1.751 552 | <1 | 1.751 600 | 100 000 | 1.751 600 | <1 | ||||
| CST6-1 | 1.810 077 | 3 169 | 1.810 800 | 1 | 1.810 077 | <1 | 1.810 100 | 100 000 | 1.810 100 | <1 | ||||
| CST7-1 | 1.838 724 | 5 152 | 1.838 800 | 1 | 1.838 724 | <1 | 1.838 800 | 100 000 | 1.838 800 | <1 | ||||
| CST8-1 | 1.864 532 | 8 428 | 1.858 500 | 1 | 1.858 401 | <1 | 1.858 500 | 100 000 | 1.858 500 | <1 | ||||
| CST9-1 | 1.878 813 | 10 489 | 1.878 900 | 1 | 1.878 813 | <1 | 1.878 900 | 100 000 | 1.878 900 | <1 | ||||
| CST10-1 | 1.920 960 | 14 739 | 1.913 500 | 3 | 1.913 436 | 2 | 1.913 500 | 100 000 | 1.913 500 | <1 | ||||
| CST12-1 | 1.959 311 | 10 919 | 1.949 900 | 37 | 1.949 824 | 5 | 1.949 900 | 100 000 | 1.949 900 | 12 | ||||
| CST14-1 | 2.006 005 | 14 885 | 1.986 300 | 54 | 1.983 071 | 12 | 1.980 300 | 100 000 | 1.981 000 | 35 | ||||
| CST16-1 | 2.031 021 | 22 418 | 2.008 400 | 13 | 2.008 386 | 31 | 2.004 600 | 100 000 | 2.004 700 | 58 | ||||
| CST18-1 | 2.065 764 | 25 499 | 2.039 700 | 70 | 2.048 725 | 14 | 2.028 100 | 100 000 | 2.032 700 | 43 | ||||
| CST20-1 | 2.083 187 | 38 164 | 2.071 600 | 93 | 2.074 201 | 35 | 2.051 500 | 100 000 | 2.060 200 | 65 | ||||
| CST25-1 | 2.143 192 | 30 929 | 2.123 600 | 37 | 2.124 727 | 22 | 2.097 600 | 100 000 | 2.112 400 | 44 | ||||
| CST30-1 | 2.188 324 | 63 970 | 2.167 900 | 72 | 2.170 038 | 10 | 2.140 000 | 100 000 | 2.156 800 | 83 | ||||
| CST35-1 | 2.220 271 | 90 387 | 2.203 700 | 367 | 2.209 698 | 16 | 2.171 900 | 100 000 | 2.194 100 | 97 | ||||
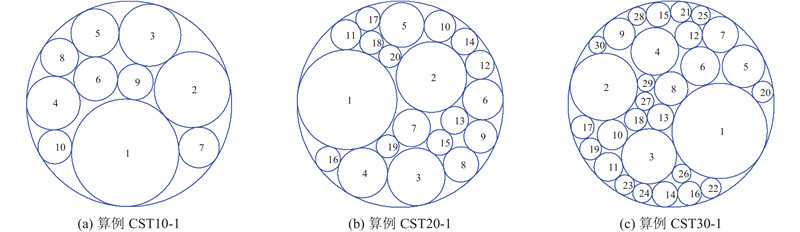
图 4
图 4 SILDA在算例CST10-1、CST20-1和CST30-1上的布局结果图
Fig.4 Packing layouts found by SILDA on instances CST10-1, CST20-1 and CST30-1
上述实验从工程算例和基准函数算例2个方面验证SILDA的性能. 虽然基于不同的实验平台和编程语言,各个算例的计算时间不能作为主要评价指标,但是从解的质量和算法所耗时间2个方面综合比较,仍可清晰地表明SILDA的高效性能. SILDA不仅在满足工程应用方面更为突出,而且具有一定的理论价值.
以基准函数算例为例分析SILDA的适应性. 不同的算例包含的圆饼大小和个数各不相同,对应解空间的维数也不同. 对SILDA而言,不同的算例代表不同的求解环境. 对于同一算例,由于解空间的非连续、非线性等特点,SILDA从不同的初始解出发面临的求解环境一般也不同. 因此,SILDA在求解不等圆Packing问题时面临的是动态环境. 表4在表3的基础上进一步给出了SILDA在基准函数算例上所得容器半径的最差值、平均值和标准差. 由表4可以看出,对于14个基准函数算例,独立运行SILDA 20次均能得到较好的结果,说明SILDA对动态环境具有较强的适应性. 这是因为SILDA继承了群智能劳动分工能适应环境变化的特点,在动态环境下也能实现有效的空间分配. 群智能劳动分工对环境的适应性源于个体的行为柔性,即个体能够根据环境变化调整所执行的任务. 个体的行为柔性在SILDA中体现为圆饼的动作柔性,即圆饼在刺激-响应原理作用下可根据环境变化选择恰当的动作.
表 4 SILDA在第2组算例上的半径最优值、最差值、平均值和标准差
Tab.4
| 算例 | Rmin | |||
| 最优值 | 最差值 | 平均值 | 标准差 | |
| CST5-1 | 1.751 6 | 1.760 0 | 1.755 8 | 0.004 2 |
| CST6-1 | 1.810 1 | 1.837 2 | 1.826 2 | 0.011 6 |
| CST7-1 | 1.838 8 | 1.889 9 | 1.852 6 | 0.019 9 |
| CST8-1 | 1.858 5 | 1.890 0 | 1.870 6 | 0.010 6 |
| CST9-1 | 1.878 9 | 1.890 1 | 1.885 0 | 0.005 7 |
| CST10-1 | 1.913 5 | 2.000 0 | 1.972 5 | 0.038 9 |
| CST12-1 | 1.949 9 | 2.123 9 | 2.014 0 | 0.082 7 |
| CST14-1 | 1.981 0 | 2.098 8 | 2.039 9 | 0.051 6 |
| CST16-1 | 2.004 7 | 2.099 2 | 2.058 1 | 0.042 7 |
| CST18-1 | 2.032 7 | 2.139 8 | 2.098 5 | 0.044 4 |
| CST20-1 | 2.060 2 | 2.157 4 | 2.134 0 | 0.030 6 |
| CST25-1 | 2.112 4 | 2.180 3 | 2.161 8 | 0.025 2 |
| CST30-1 | 2.156 8 | 2.230 5 | 2.203 2 | 0.028 8 |
| CST35-1 | 2.194 1 | 2.260 3 | 2.239 8 | 0.022 6 |
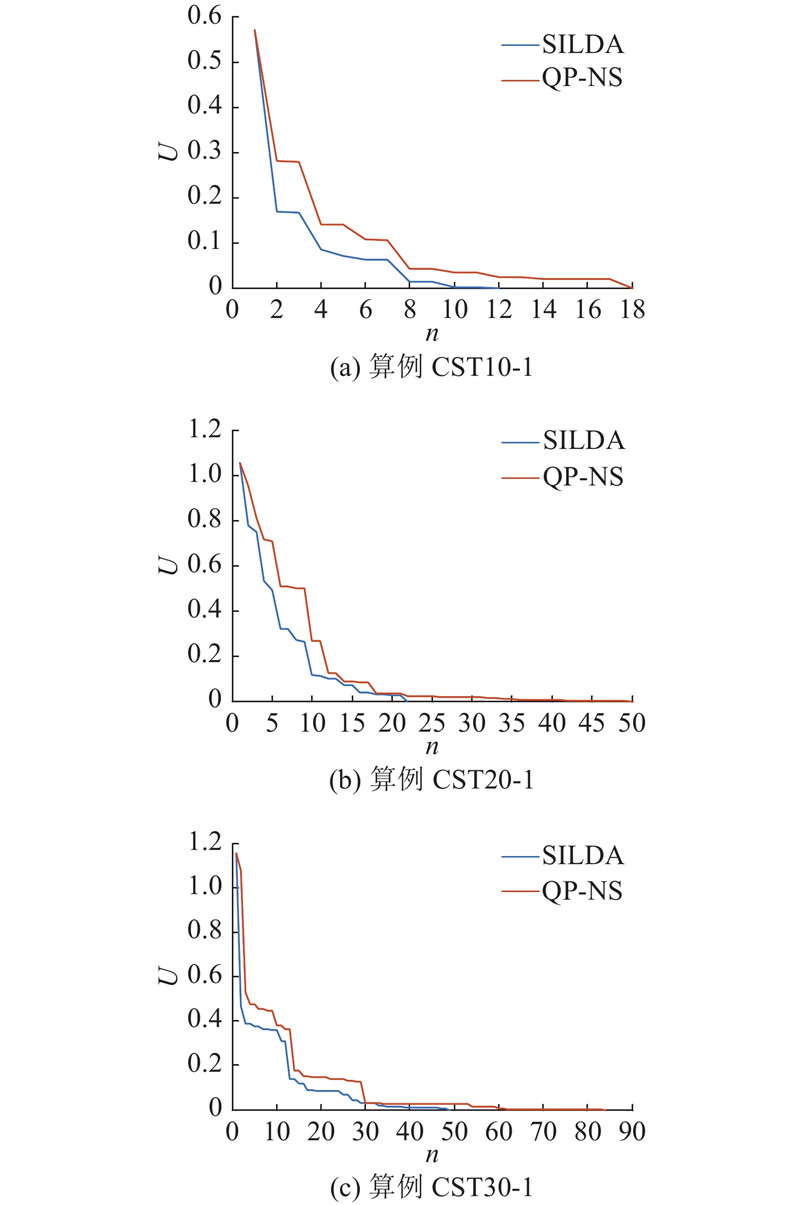
图 5
图 5 SILDA与QP-NS在不同算例上的弹性势能演化对比
Fig.5 Comparison of elastic potential energy evolution process for SILDA and QP-NS on different instances
在算法执行方面,SILDA、QP-NS都是通过圆饼执行交换动作来改进布局,且都是交换半径相近或者位置相邻的圆饼. 不同的是,QP-NS以随机的方式选择圆饼执行交换动作,SILDA以刺激-响应的方式选择圆饼执行交换动作. 在随机方式下,不论求解环境如何变化,每个圆饼都以相同的概率执行交换动作. 在刺激-响应方式下,圆饼执行交换动作的概率会随着环境改变. 比如,对于同一个圆饼,当布局解较差或者自身位置较差时执行交换动作的概率较大,而当布局解较好或者自身位置较好时执行交换动作的概率较小. 随机方式具有盲目性,刺激-响应方式具有适应性. 图5中的有效动作指使格局改进的交换动作. 可以看出,SILDA执行较少的交换动作就能找到当前容器半径下的最优布局,说明SILDA中的交换动作比QP-NS的更有效.
4. 结 语
将空间分配求解思路引入不等圆Packing问题,提出群智能劳动分工方法SILDA. SILDA采用刺激-响应方式搜索最优格局,继承群智能劳动分工行为柔性的特点,提高了算法的适应能力. 对20个代表性算例的计算结果表明,SILDA是求解不等圆Packing问题的有效算法.
由Packing问题的空间分配特性可知,通过设计恰当的动作、刺激和阈值,SILDA可用于其他Packing问题的求解. 同时,Packing问题与Cutting问题、Loading问题、背包问题等非常类似,相关成果具有一定的推广价值. 未来可以从这几个方向进行研究.
参考文献
求解不等圆Packing问题的带全局变换禁忌搜索算法
[J].
Tabu search algorithm combined with global perturbation for packing arbitrary sized circles into a circular container
[J].
求解带平衡约束圆形Packing问题的改进人工蜂群算法
[J].DOI:10.3969/j.issn.1000-2758.2014.02.016 [本文引用: 1]
Exploring improved artificial bee colony algorithm for solving circle packing problem with equilibrium constraints
[J].DOI:10.3969/j.issn.1000-2758.2014.02.016 [本文引用: 1]
动作空间带平衡约束圆形Packing问题的拟物求解算法
[J].
Quasi-physical algorithm based on action space for solving the circles packing problem with equilibrium constraints
[J].
一种求解不等圆Packing问题的改进遗传模拟退火算法
[J].DOI:10.3969/j.issn.1000-2758.2017.06.015 [本文引用: 10]
An improved genetic stimulated annealing algorithm to solve the unequal circle packing problem
[J].DOI:10.3969/j.issn.1000-2758.2017.06.015 [本文引用: 10]
An improved algorithm for the packing of unequal circles within a larger containing circle
[J].DOI:10.1016/S0377-2217(01)00241-7 [本文引用: 2]
不等圆Packing问题的拟物型邻域搜索算法
[J].
Neighborhood search algorithm associated with quasi-pgysical method for solving unequal circle packing problem
[J].
Packing unequal circles using formulation space search
[J].DOI:10.1016/j.cor.2012.11.022 [本文引用: 1]
A formulation space search heuristic for packing unequal circles in a fixed size circular container
[J].DOI:10.1016/j.ejor.2015.10.062 [本文引用: 1]
An improved energy landscape paving algorithm for the problem of packing circles into a larger containing circle
[J].DOI:10.1016/j.cie.2009.05.010 [本文引用: 1]
求解带平衡性能约束的圆形装填问题的吸引盘填充算法
[J].
Basin filling algorithm for the circular packing problem with equilibrium behavioral constraints
[J].
Iterated tabu search for the circular open dimension problem
[J].DOI:10.1016/j.ejor.2012.10.022 [本文引用: 1]
Iterated Tabu search and variable neighborhood descent for packing unequal circles into a circular container
[J].DOI:10.1016/j.ejor.2015.09.001 [本文引用: 3]
New heuristics for packing unequal circles into a circular container
[J].DOI:10.1016/j.cor.2005.01.003 [本文引用: 1]
PERM for solving circle packing problem
[J].DOI:10.1016/j.cor.2006.10.012 [本文引用: 1]
A beam search algorithm for the circular packing problem
[J].DOI:10.1016/j.cor.2008.02.003 [本文引用: 1]
Adaptive beam search lookahead algorithms for the circular packing problem
[J].DOI:10.1111/j.1475-3995.2009.00745.x [本文引用: 1]
A dynamic adaptive local search algorithm for the circular packing problem
[J].DOI:10.1016/j.ejor.2005.11.069 [本文引用: 1]
Packing circles in the smallest circle: an adaptive hybrid algorithm
[J].DOI:10.1057/jors.2010.157 [本文引用: 3]
Labour division in swarm intelligence for allocation problems: a survey
[J].DOI:10.1504/IJBIC.2018.094186 [本文引用: 2]
面向群体利益分配的蚁群劳动分工建模与仿真
[J].DOI:10.3969/j.issn.1007-9807.2016.10.001 [本文引用: 1]
Modeling and simulation of ant colony’s labor division for interests allocation of social groups
[J].DOI:10.3969/j.issn.1007-9807.2016.10.001 [本文引用: 1]
Modeling and simulation of dynamic ant colony’s labor division for task allocation of UAV swarm
[J].DOI:10.1016/j.physa.2017.08.094
A flexible labour division approach to the polygon packing problem based on space allocation
[J].DOI:10.1080/00207543.2016.1229070 [本文引用: 1]
An evolutionary perspective on self-organized labor division in social insects
[J].DOI:10.1146/annurev-ecolsys-102710-145017 [本文引用: 1]
Quantitative study of the fixed threshold model for the regulation of division of labour in insect societies
[J].DOI:10.1098/rspb.1996.0229 [本文引用: 1]
Response threshold reinforcements and division of labour in insect societies
[J].DOI:10.1098/rspb.1998.0299 [本文引用: 1]