传统的直接数字频率综合器采用只读内存(read only memory, ROM)查找表完成从累加器输出相位到幅度的转换,然后经数模转换器(digital to analog converter, DAC)和低通滤波器(low pass filter, LPF)完成数字信号到模拟信号的转换[8]. 将CORDIC算法应用于DDFS中的相幅转换模块,与ROM查找表相比,可以有效降低高精度DDFS所需占用的存储资源,提高电路速度.
传统的流水线迭代式CORDIC算法依赖于迭代次数保证算法精度,本次迭代的旋转方向需要等待上次迭代完成才能确定[9]. 对于精度要求高的情况,需要迭代很多次,导致输出时延过长,硬件消耗大. 随着数字通信系统向实时性和高集成度趋势的发展,研究者们提出多种改进方案:史方显等[10]提出选择迭代式的CORDIC算法,有效减少了迭代次数,但z通路的复杂运算使得其存在硬件消耗较大的问题. 张佳等[11]设计的三角函数运算单元提高了精度,但所耗费的资源很大. 徐成等[12]提出免除缩放因子的双步旋转机制,将两次基本旋转合并成一次迭代,减少了一半的迭代次数,但输出时延很大;祁艳杰等[13]采用并行CORDIC算法模块代替查找表,对进位保存加法器进行改进,提高了运算速度,但所消耗的资源增加,精度较低.
针对目前CORDIC算法实现时存在的时延大和资源消耗大的问题,结合三步旋转机制、角度二极化重编码技术和合并迭代技术,提出改进的低时延低消耗CORDIC算法. 结合加法树技术,实现了20位定点小数的高精度低时延DDFS,与其他方案相比,在资源、时延和精度上都有优化.
1. 三步旋转CORDIC算法
1.1. 角度二极化重编码
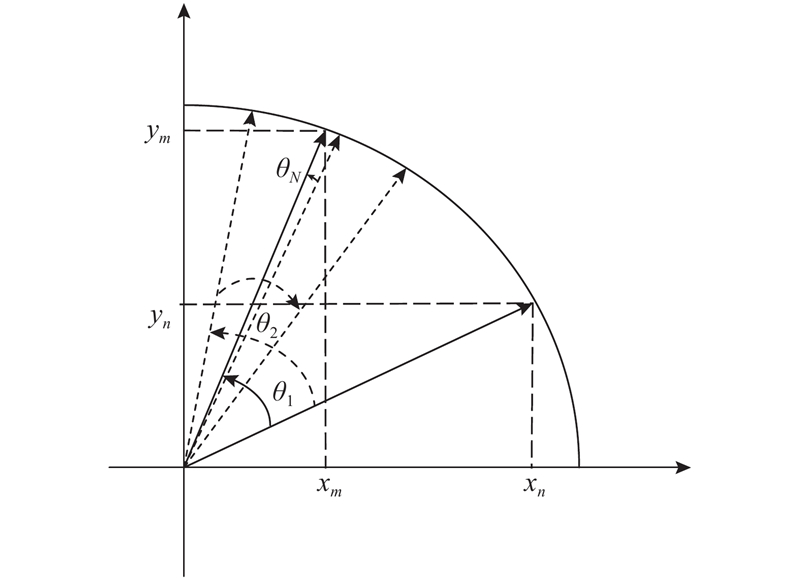
CORDIC的基本思想如下:通过基本角度集
图 1
以流水线迭代方式实现CORDIC算法时,取
根据如下迭代公式,以流水线结构完成迭代[9]:
引入的
考虑到
式中:
与取
1.2. 三步旋转与多路选择器
经过角度二极化重编码处理后,单次的旋转迭代公式变为
对
对于
式(8)省去了中间迭代的过程,从
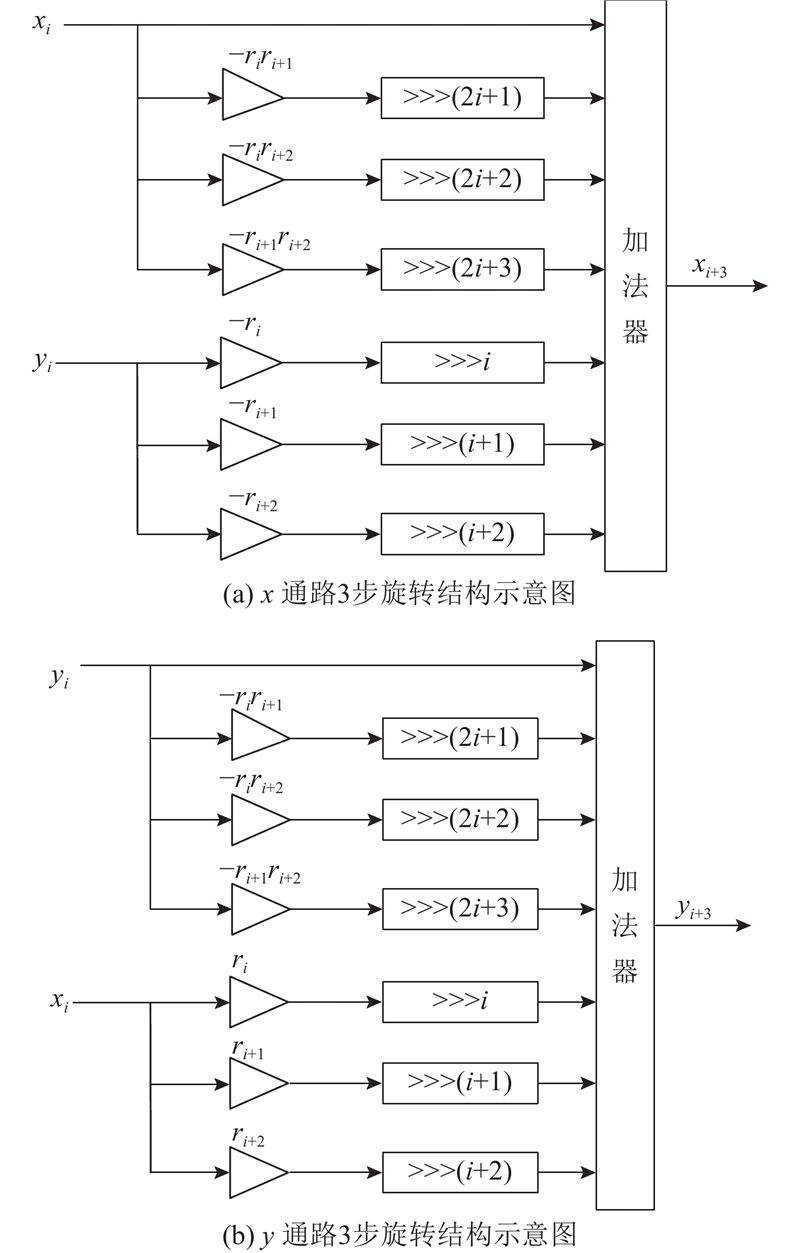
图 2
三步旋转可以在1个时钟周期内完成3次迭代,减少了迭代次数. 通过图2可以看出,相比于式(6)的迭代,三步旋转可以节省硬件资源.
对于
根据式(6)和r3, ···, rm−2, rm−1的所有可能取值线下计算出
1.3. 合并迭代和区间折叠
对于
当
由式(11)可知,这一阶段由
对于
可以看出,对
2. 三步旋转CORDIC算法的实现
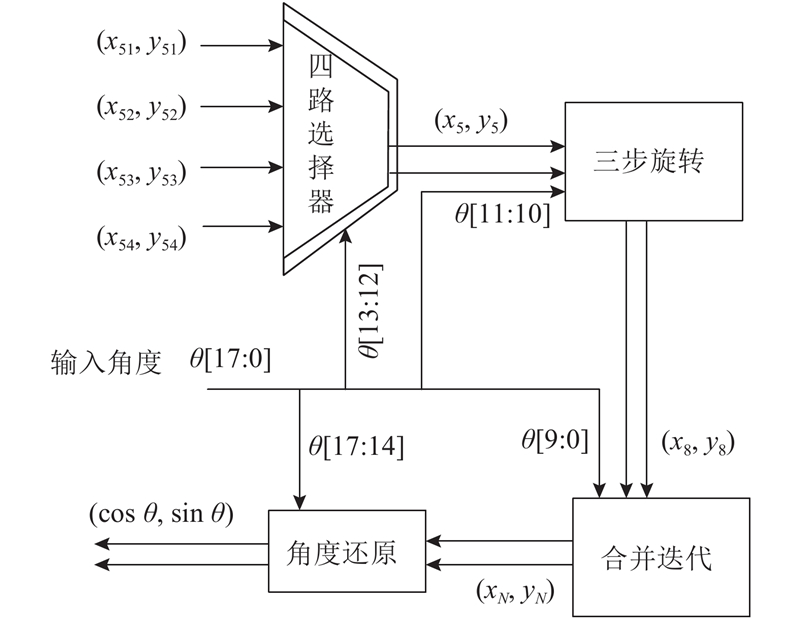
根据前面描述的算法原理,算法实现的整体流程如下:根据输入角度的二进制位值,从可能的初始值中选择正确的初始值完成第1阶段的迭代;然后通过三步旋转得到第2阶段的迭代结果,再通过合并迭代完成第3阶段的迭代;最后根据两角差公式和三角函数对称性,进行角度还原. 角度还原包括一次加法运算和缩放
图 3
图 3 三步旋转算法实现框图
Fig.3 Block diagram of three-step rotation algorithm realization
在相同的输出位宽(N=16)的情况下,比较流水线迭代式算法和三步旋转算法的误差. 利用Matlab实现了流水线迭代式CORDIC算法和提出的三步旋转算法,开展定点化误差仿真,仿真时输入角度的分辨率取2−15,角度取
表 1 2种算法的性能对比
Tab.1
| 算法 | 最大幅值 误差/10 −5 | 硬件开销 LUT+FF | 输出时延 |
| 传统流水线算法 | 43.7 | 1 619 | 16 Tclk |
| 三步旋转算法 | 18.7 | 1 146 | 4 Tclk |
从表1 可以看出,三步旋转算法的查找表(look-up table, LUT)和寄存器(flip-flop, FF)开销总共为1 146个,与传统流水线算法相比,硬件开销下降了29.2%;三步旋转CORDIC算法的输出时延为4个时钟周期(Tclk),与传统流水线算法相比下降了75%,这是由于三步旋转算法采用三步旋转和合并迭代的方法对迭代次数进行了压缩. 三步旋转CORDIC算法的最大幅值误差为18.7×10−5,比传统算法的误差小. 传统算法采用θi=arctan (2−i)的线性组合来逼近输入角度
3. 基于三步旋转CORDIC算法的DDFS实现
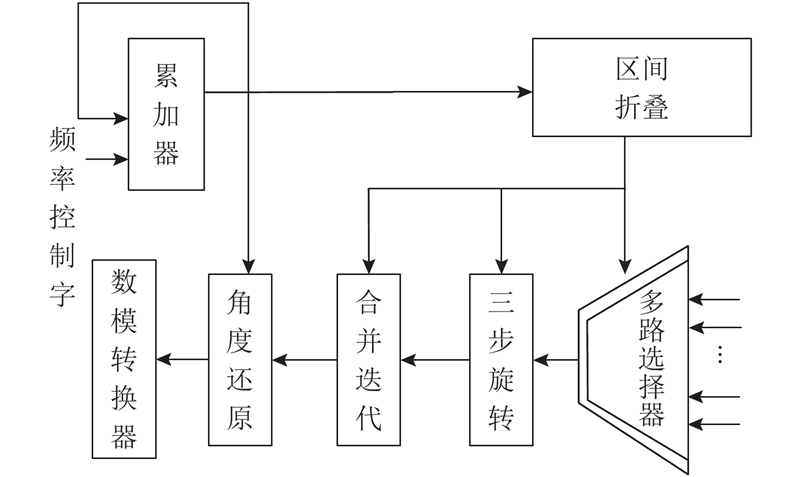
利用改进的三步旋转CORDIC算法,实现DDFS中的相幅转换模块,并将结果送到DAC,结构框图如图4所示. 累加器负责对频率控制字进行累加,将累加得到的角度进行区间折叠;然后将角度转换到
图 4
3.1. 相位累加器和加法树
相位累加器对给定的频率控制字进行累加得到相位,当累加到
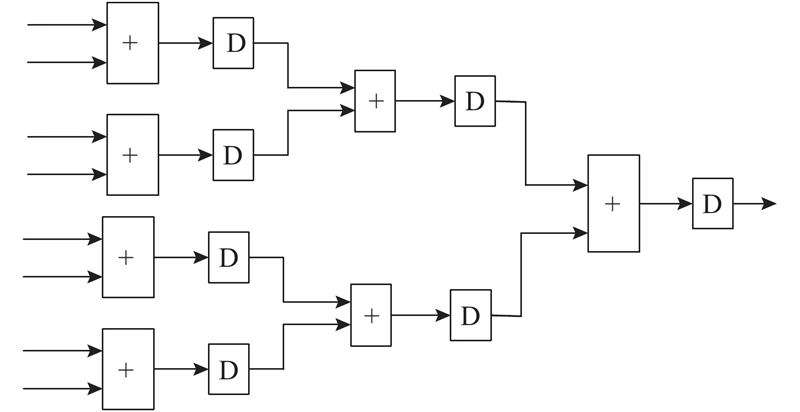
为了提高电路的系统速度,对算法中多输入的加法器进行优化. 采用加法树结构将加法运算流水化,可以使电路满足更严格的时序约束,提高电路的系统时钟频率. 3级加法树结构的示意图如图5所示,即将操作数两两相加;然后用流水线寄存器进行寄存,对寄存后的结果进行两两相加然后寄存,直到最后一级输出. 算法实现时考虑速度和资源的折中,可以调整单级加法树中加法器的输入个数.
图 5
3.2. DDFS的实现与仿真结果分析
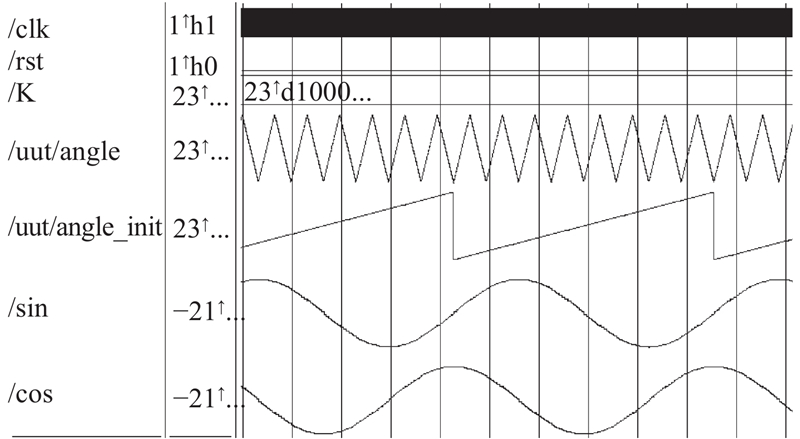
图 6
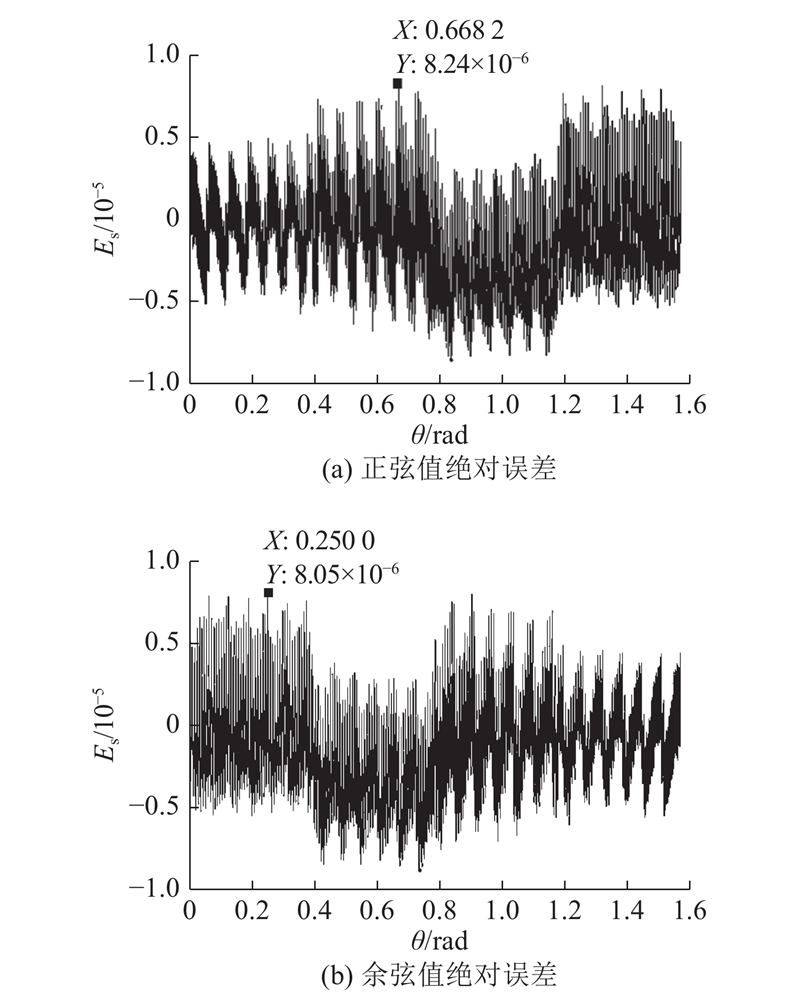
图 7
图 7 三步旋转CORDIC算法的正、余弦值绝对误差
Fig.7 Sine and cosine absolute error of three-step rotation CORDIC algorithm
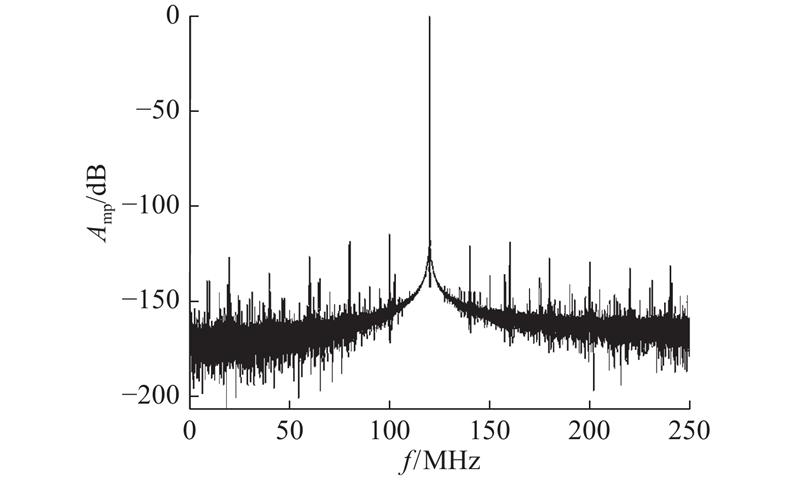
将算法实现后输出的数据导入Matlab中,对输出波形进行频谱分析,计算出无杂散动态范围(spurious free dynamic range, SFDR). 输出信号频率为120 MHz时的频谱图(500 MHz采样频率)如图8所示. 图中,f为信号频率,Amp为信号幅度,SFDR为105.03 dB.
图 8
图 8 输出频率为120 MHz时的输出信号频谱图
Fig.8 Spectrum of output signal when output frequency is 120 MHz
对于实现的Verilog代码进行综合,选择Xilinx的XC5VLX30型号的现场可编程门阵列(field programmable gate array, FPGA)芯片. 基于该算法和文献[10]、[13]、[18]算法实现的DDFS的最大幅度误差、输出时延及硬件消耗的对比,如表2所示. 可以看出,本文的硬件开销比文献[10]、[13]都小,这是由于采用角度二极化重编码省去了剩余旋转角度的计算,即消除了z通路的运算. 角度二极化重编码后旋转的角度是直接由角度的位值决定的,这使得本文的精度更高. Xin等[18]采用循环迭代和流水线相结合的方法,重复使用移位寄存器和加法器减少了硬件开销,但是这使得输出时延很大. 虽然Xin等[18]的硬件开销为本文的37.48%,但是输出时延是本文的4.27倍. 本文采用三步旋转和合并迭代技术极大地压缩了迭代次数,利用加法树对多输入加法器进行适当的优化,提高了电路的工作频率,达到了更低的输出时延,即38.5 ns.
表 2 4种方案的最大幅度误差、输出时延及硬件消耗对比
Tab.2
4. 结 语
针对流水线迭代式CORDIC算法硬件开销大和输出时延大的缺点,提出基于三步旋转机制的低时延低消耗CORDIC算法. 从数学上分析三步旋转算法降低时延和资源消耗的原理,即利用三步旋转和合并迭代压缩迭代次数,结合区间折叠和角度二极化重编码技术消除剩余旋转角度运算通路;用Verilog语言实现了算法,通过仿真对比三步旋转算法和流水线迭代式算法的性能. Matlab仿真结果和Vivado综合结果表明:与流水线迭代式CORDIC算法相比,在精度稍有改善的情况下,三步旋转算法的硬件开销降低了约29.2%,从输入角度到输出正余弦值的时延减少了75%. 利用该算法,结合加法树技术实现了DDFS. 仿真结果表明,与以往的实现方案相比,在精度、硬件开销和输出时延方面均有一定的优化.
参考文献
Algorithm and design of a fully parallel approximate coordinate rotation digital computer (CORDIC)
[J].DOI:10.1109/TMSCS.2017.2696003 [本文引用: 1]
Concept, design, and implementation of reconfigurable CORDIC
[J].DOI:10.1109/TVLSI.2015.2445855 [本文引用: 1]
Singular value decomposition using an array of CORDIC processors
[J].DOI:10.1016/j.sigpro.2014.03.022 [本文引用: 1]
Low-power DCT-based compressor for wireless capsule endoscopy
[J].DOI:10.1016/j.image.2017.03.003
Design of DDS based on hybird-CORDIC architecture
[J].DOI:10.1080/18756891.2011.9727787
Design and implementation of hybrid CORDIC algorithm based on phase rotation estimation for NCO
[J].
The CORDIC trigonometric computing technique
[J].DOI:10.1109/TEC.1959.5222693 [本文引用: 2]
改进型高速高精度CORDIC算法及其在DDFS中的应用
[J].DOI:10.3969/j.issn.0372-2112.2017.02.025 [本文引用: 4]
Direct digital frequency synthesizer based on an improved high speed and high precision CORDIC algorithm
[J].DOI:10.3969/j.issn.0372-2112.2017.02.025 [本文引用: 4]
一种80位扩展双精度浮点三角函数运算单元的设计
[J].
Design of a 80 bits extended double precision floating-point trigonometric computing unit
[J].
免缩放因子双步旋转CORDIC算法
[J].DOI:10.3969/j.issn.0372-2112.2014.07.031 [本文引用: 1]
Double-step scaling free CORDIC
[J].DOI:10.3969/j.issn.0372-2112.2014.07.031 [本文引用: 1]
基于Parallel_CORDIC的高精度高速度直接数字频率合成器的FPGA实现
[J].DOI:10.3969/j.issn.0372-2112.2014.07.023 [本文引用: 4]
FPGA implementation of high speed and high precision direct digital frequency synthesizer based on Parallel_CORDIC
[J].DOI:10.3969/j.issn.0372-2112.2014.07.023 [本文引用: 4]
A 100-MHz, 16-b, direct digital frequency synthesizer with a 100-dBc spurious-free dynamic range
[J].DOI:10.1109/4.777100 [本文引用: 1]
基于CORDIC改进算法的高速DDS电路设计
[J].
Implement of high speed DDS circuit design using improved CORDIC algorithm
[J].
Para-CORDIC: parallel CORDIC rotation algorithm
[J].DOI:10.1109/TCSI.2004.832734 [本文引用: 1]
超低时延免迭代 CORDIC 算法
[J].DOI:10.3969/j.issn.1001-2400.2017.04.028 [本文引用: 1]
Ultra-low latency and omit-iteration CORDIC algorithm
[J].DOI:10.3969/j.issn.1001-2400.2017.04.028 [本文引用: 1]