[1]
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks [C] // International Conference on Neural Information Processing Systems . Lake Tahoe: Curran Associates Inc., 2012.
[本文引用: 2]
[2]
GRAVES A, SCHMIDHUBER J Framewise phoneme classification with bidirectional LSTM and other neural network architectures
[J]. Neural Netw , 2005 , 18 (5 ): 602 - 610
[本文引用: 1]
[3]
SZEGEDY C, VANHOUCKE V, IOFFE S, et al. Rethinking the inception architecture for computer vision [C] // International Conference on Computer Vision and Pattern Recognition . Las Vegas: IEEE, 2016: 2818-2826.
[本文引用: 1]
[4]
DENIL M, SHAKIBI B, DINH L, et al. Predicting parameters in deep learning [C] // Advances in Neural Information Processing Systems . Lake Tahoe: MIT, 2013: 2148-2156.
[本文引用: 2]
[5]
SRINIVAS S, BABU R V. Data-free parameter pruning for deep neural networks [EB/OL]. [2018-09-06]. http://arxiv.org/abs/1507.06149.
[本文引用: 1]
[6]
HAN S, POOL J, TRAN J, et al. Learning both weights and connections for efficient neural network [C] // Advances in Neural Information Processing Systems . Montreal: MIT, 2015: 1135-1143.
[本文引用: 1]
[7]
MARIET Z, SRA S. Diversity networks: neural network compression using determinantal point processes [EB/OL]. [2018-05-13]. http://arxiv.org/abs/1511.05077.
[本文引用: 1]
[8]
HAN S, MAO H, DALLY W J. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding [EB/OL]. [2018-08-09]. http://arxiv.org/abs/1510.00149.
[本文引用: 2]
[9]
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition [EB/OL]. [2018-07-22]. http://arxiv.org/abs/1409.1556.
[本文引用: 1]
[10]
IANDOLA F N, HAN S, MOSKEWICZ M W, et al. Squeezenet: Alexnet-level accuracy with 50x fewer parameters and < 0.5 mb model size [EB/OL]. [2018-07-14]. http://arxiv.org/abs/1602.07360.
[本文引用: 1]
[11]
HAN S, LIU X, MAO H, et al EIE: efficient inference engine on compressed deep neural network
[J]. ACM Sigarch Computer Architecture News , 2016 , 44 (3 ): 243 - 254
DOI:10.1145/3007787.3001163
[本文引用: 1]
[12]
MATHIEU M, HENAFF M, LECUN Y. Fast training of convolutional networks through FFTs [EB/OL]. [2018-09-03]. http://arxiv.org/abs/1312.5851.
[本文引用: 1]
[13]
RASTEGARI M, ORDONEZ V, REDMON J, et al. XNOR-Net: ImageNet classification using binary convolutional neural networks [C] // European Conference on Computer Vision . Cham: Springer, 2016: 525-542.
[本文引用: 1]
[14]
WEN W, WU C, WANG Y, et al. Learning structured sparsity in deep neural networks [C] // Advances in Neural Information Processing Systems . Barcelona: MIT, 2016: 2074-2082.
[本文引用: 1]
[15]
LI H, KADAV A, DURDANOVIC I, et al. Pruning filters for efficient convents [EB/OL]. [2018-09-11]. http://arxiv.org/abs/1608.08710.
[本文引用: 4]
[16]
MITTAL D, BHARDWAJ S, KHAPRA M M, et al. Recovering from random pruning: on the plasticity of deep convolutional neural networks [EB/OL]. [2018-09-12]. http://arxiv.org/abs/1801.10447.
[本文引用: 2]
[17]
ZHU M, GUPTA S. To prune, or not to prune: exploring the efficacy of pruning for model compression [EB/OL]. [2018-06-23]. http://arxiv.org/abs/1710.01878.
[本文引用: 1]
[18]
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition [C] // Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Las Vegas: IEEE, 2016: 770-778.
[本文引用: 1]
[19]
ZAGORUYKO S. 92.45% on CIFAR-10 in Torch[EB/OL].[2018-07-30]. http://torch.ch/blog/2015/07/30/cifar.html.
[本文引用: 1]
[20]
IOFFE S, SZEGEDY C. Batch normalization: accelerating deep network training by reducing internal covariate shift [EB/OL]. [2018-07-16]. http://arxiv.org/abs/1502.03167.
[本文引用: 1]
[21]
HU H, PENG R, TAI Y W, et al. Network trimming: a data-driven neuron pruning approach towards efficient deep architectures [EB/OL]. [2018-07-19]. http://arxiv.org/abs/1607.03250.
[本文引用: 1]
[22]
MOLCHANOV P, TYREE S, KARRAS T, et al. Pruning convolutional neural networks for resource efficient transfer learning [EB/OL]. [2018-07-03]. http://arxiv.org/abs/1611.06440.
[本文引用: 1]
2
... 卷积神经网络(convolutional neural network,CNN)已成为一种重要的非线性自适应信息处理方法,在多个领域得到了广泛应用,并且在多种任务中取得了突出的成果[1 -2 ] .随着网络层数的增加,神经网络对计算平台的运算速度和存储资源提出了越来越高的要求,其在计算资源有限的嵌入式平台上难以发挥优异的性能. 对于在嵌入式和移动端的应用,准确率和运行速度同等重要[3 ] . ...
... 多种深度学习模型已经证明存在着大量的参数冗余[4 ] ,带有冗余参数的模型不仅浪费存储空间和计算资源,而且容易导致过拟合问题.近年来,研究者在网络模型压缩方面作了大量的工作[5 -7 ] ,Han等[8 ] 基于AlexNet[1 ] 和VGGNet[9 ] 实现了基于权重裁剪的算法,通过重新训练弥补准确率损失,该算法主要裁减全连接层的参数,而神经网络的计算消耗主要来自卷积层,所以该算法不能明显提升模型的计算效率. 为了降低卷积层的计算消耗,Iandola等[10 ] 实现了利用稀疏矩阵计算库和特殊硬件[11 ] 压缩卷积层的算法. Denil等[4 ] 实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
Framewise phoneme classification with bidirectional LSTM and other neural network architectures
1
2005
... 卷积神经网络(convolutional neural network,CNN)已成为一种重要的非线性自适应信息处理方法,在多个领域得到了广泛应用,并且在多种任务中取得了突出的成果[1 -2 ] .随着网络层数的增加,神经网络对计算平台的运算速度和存储资源提出了越来越高的要求,其在计算资源有限的嵌入式平台上难以发挥优异的性能. 对于在嵌入式和移动端的应用,准确率和运行速度同等重要[3 ] . ...
1
... 卷积神经网络(convolutional neural network,CNN)已成为一种重要的非线性自适应信息处理方法,在多个领域得到了广泛应用,并且在多种任务中取得了突出的成果[1 -2 ] .随着网络层数的增加,神经网络对计算平台的运算速度和存储资源提出了越来越高的要求,其在计算资源有限的嵌入式平台上难以发挥优异的性能. 对于在嵌入式和移动端的应用,准确率和运行速度同等重要[3 ] . ...
2
... 多种深度学习模型已经证明存在着大量的参数冗余[4 ] ,带有冗余参数的模型不仅浪费存储空间和计算资源,而且容易导致过拟合问题.近年来,研究者在网络模型压缩方面作了大量的工作[5 -7 ] ,Han等[8 ] 基于AlexNet[1 ] 和VGGNet[9 ] 实现了基于权重裁剪的算法,通过重新训练弥补准确率损失,该算法主要裁减全连接层的参数,而神经网络的计算消耗主要来自卷积层,所以该算法不能明显提升模型的计算效率. 为了降低卷积层的计算消耗,Iandola等[10 ] 实现了利用稀疏矩阵计算库和特殊硬件[11 ] 压缩卷积层的算法. Denil等[4 ] 实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
... [4 ]实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
1
... 多种深度学习模型已经证明存在着大量的参数冗余[4 ] ,带有冗余参数的模型不仅浪费存储空间和计算资源,而且容易导致过拟合问题.近年来,研究者在网络模型压缩方面作了大量的工作[5 -7 ] ,Han等[8 ] 基于AlexNet[1 ] 和VGGNet[9 ] 实现了基于权重裁剪的算法,通过重新训练弥补准确率损失,该算法主要裁减全连接层的参数,而神经网络的计算消耗主要来自卷积层,所以该算法不能明显提升模型的计算效率. 为了降低卷积层的计算消耗,Iandola等[10 ] 实现了利用稀疏矩阵计算库和特殊硬件[11 ] 压缩卷积层的算法. Denil等[4 ] 实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
1
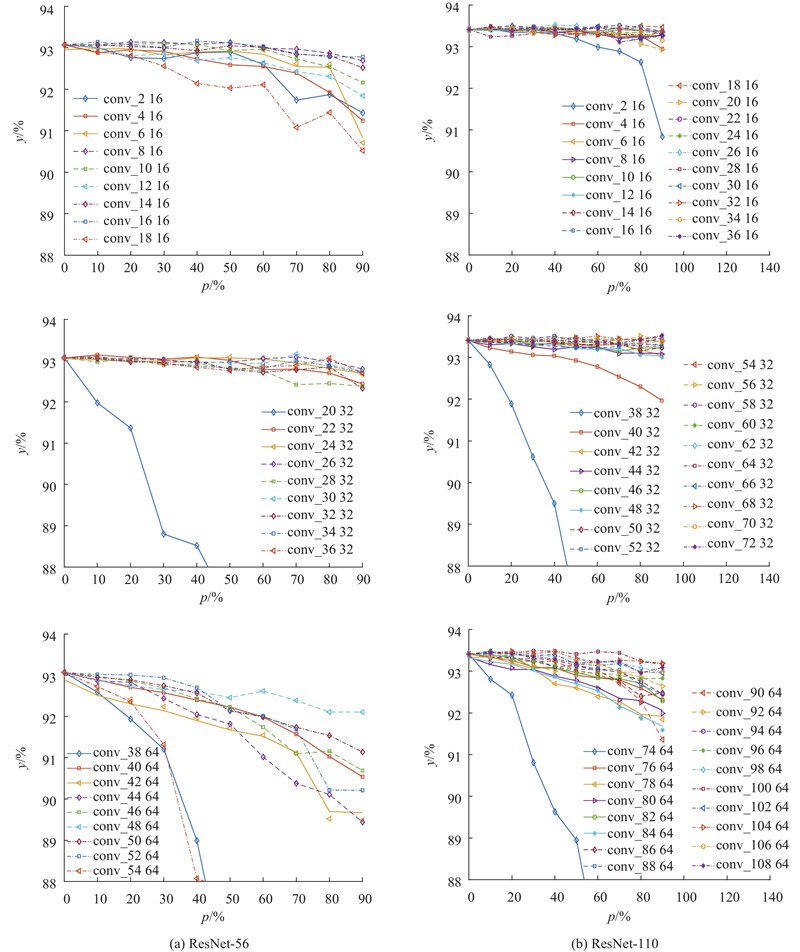
... Han等[6 ] 的工作是基于逐层权重裁剪和重训练的方式,通过逐层迭代弥补精度损失. 对于深层网络,逐层裁剪和重训练的迭代方式非常消耗时间. 本文算法通过单层裁剪分析网络的整体稳健性作为网络裁剪的基础,通过单次的裁剪和重训练恢复模型精度,提高了模型压缩流程的效率. 本文根据网络层的裁剪敏感度设置该层的裁剪占比,对于VGG-16等深层网络,根据网络中特征图的尺寸大小将网络分为若干阶段,同阶段特征图尺寸相同. 实验结果表明,同阶段卷积层的敏感度几乎一样,为了避免引入其他超参数,对于同阶段的所有卷积层采用相同的裁剪占比,简化裁剪流程. ...
1
... 多种深度学习模型已经证明存在着大量的参数冗余[4 ] ,带有冗余参数的模型不仅浪费存储空间和计算资源,而且容易导致过拟合问题.近年来,研究者在网络模型压缩方面作了大量的工作[5 -7 ] ,Han等[8 ] 基于AlexNet[1 ] 和VGGNet[9 ] 实现了基于权重裁剪的算法,通过重新训练弥补准确率损失,该算法主要裁减全连接层的参数,而神经网络的计算消耗主要来自卷积层,所以该算法不能明显提升模型的计算效率. 为了降低卷积层的计算消耗,Iandola等[10 ] 实现了利用稀疏矩阵计算库和特殊硬件[11 ] 压缩卷积层的算法. Denil等[4 ] 实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
2
... 多种深度学习模型已经证明存在着大量的参数冗余[4 ] ,带有冗余参数的模型不仅浪费存储空间和计算资源,而且容易导致过拟合问题.近年来,研究者在网络模型压缩方面作了大量的工作[5 -7 ] ,Han等[8 ] 基于AlexNet[1 ] 和VGGNet[9 ] 实现了基于权重裁剪的算法,通过重新训练弥补准确率损失,该算法主要裁减全连接层的参数,而神经网络的计算消耗主要来自卷积层,所以该算法不能明显提升模型的计算效率. 为了降低卷积层的计算消耗,Iandola等[10 ] 实现了利用稀疏矩阵计算库和特殊硬件[11 ] 压缩卷积层的算法. Denil等[4 ] 实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
... [8 ]、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
1
... 多种深度学习模型已经证明存在着大量的参数冗余[4 ] ,带有冗余参数的模型不仅浪费存储空间和计算资源,而且容易导致过拟合问题.近年来,研究者在网络模型压缩方面作了大量的工作[5 -7 ] ,Han等[8 ] 基于AlexNet[1 ] 和VGGNet[9 ] 实现了基于权重裁剪的算法,通过重新训练弥补准确率损失,该算法主要裁减全连接层的参数,而神经网络的计算消耗主要来自卷积层,所以该算法不能明显提升模型的计算效率. 为了降低卷积层的计算消耗,Iandola等[10 ] 实现了利用稀疏矩阵计算库和特殊硬件[11 ] 压缩卷积层的算法. Denil等[4 ] 实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
1
... 多种深度学习模型已经证明存在着大量的参数冗余[4 ] ,带有冗余参数的模型不仅浪费存储空间和计算资源,而且容易导致过拟合问题.近年来,研究者在网络模型压缩方面作了大量的工作[5 -7 ] ,Han等[8 ] 基于AlexNet[1 ] 和VGGNet[9 ] 实现了基于权重裁剪的算法,通过重新训练弥补准确率损失,该算法主要裁减全连接层的参数,而神经网络的计算消耗主要来自卷积层,所以该算法不能明显提升模型的计算效率. 为了降低卷积层的计算消耗,Iandola等[10 ] 实现了利用稀疏矩阵计算库和特殊硬件[11 ] 压缩卷积层的算法. Denil等[4 ] 实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
EIE: efficient inference engine on compressed deep neural network
1
2016
... 多种深度学习模型已经证明存在着大量的参数冗余[4 ] ,带有冗余参数的模型不仅浪费存储空间和计算资源,而且容易导致过拟合问题.近年来,研究者在网络模型压缩方面作了大量的工作[5 -7 ] ,Han等[8 ] 基于AlexNet[1 ] 和VGGNet[9 ] 实现了基于权重裁剪的算法,通过重新训练弥补准确率损失,该算法主要裁减全连接层的参数,而神经网络的计算消耗主要来自卷积层,所以该算法不能明显提升模型的计算效率. 为了降低卷积层的计算消耗,Iandola等[10 ] 实现了利用稀疏矩阵计算库和特殊硬件[11 ] 压缩卷积层的算法. Denil等[4 ] 实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
1
... 多种深度学习模型已经证明存在着大量的参数冗余[4 ] ,带有冗余参数的模型不仅浪费存储空间和计算资源,而且容易导致过拟合问题.近年来,研究者在网络模型压缩方面作了大量的工作[5 -7 ] ,Han等[8 ] 基于AlexNet[1 ] 和VGGNet[9 ] 实现了基于权重裁剪的算法,通过重新训练弥补准确率损失,该算法主要裁减全连接层的参数,而神经网络的计算消耗主要来自卷积层,所以该算法不能明显提升模型的计算效率. 为了降低卷积层的计算消耗,Iandola等[10 ] 实现了利用稀疏矩阵计算库和特殊硬件[11 ] 压缩卷积层的算法. Denil等[4 ] 实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
1
... 多种深度学习模型已经证明存在着大量的参数冗余[4 ] ,带有冗余参数的模型不仅浪费存储空间和计算资源,而且容易导致过拟合问题.近年来,研究者在网络模型压缩方面作了大量的工作[5 -7 ] ,Han等[8 ] 基于AlexNet[1 ] 和VGGNet[9 ] 实现了基于权重裁剪的算法,通过重新训练弥补准确率损失,该算法主要裁减全连接层的参数,而神经网络的计算消耗主要来自卷积层,所以该算法不能明显提升模型的计算效率. 为了降低卷积层的计算消耗,Iandola等[10 ] 实现了利用稀疏矩阵计算库和特殊硬件[11 ] 压缩卷积层的算法. Denil等[4 ] 实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
1
... 多种深度学习模型已经证明存在着大量的参数冗余[4 ] ,带有冗余参数的模型不仅浪费存储空间和计算资源,而且容易导致过拟合问题.近年来,研究者在网络模型压缩方面作了大量的工作[5 -7 ] ,Han等[8 ] 基于AlexNet[1 ] 和VGGNet[9 ] 实现了基于权重裁剪的算法,通过重新训练弥补准确率损失,该算法主要裁减全连接层的参数,而神经网络的计算消耗主要来自卷积层,所以该算法不能明显提升模型的计算效率. 为了降低卷积层的计算消耗,Iandola等[10 ] 实现了利用稀疏矩阵计算库和特殊硬件[11 ] 压缩卷积层的算法. Denil等[4 ] 实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
4
... 多种深度学习模型已经证明存在着大量的参数冗余[4 ] ,带有冗余参数的模型不仅浪费存储空间和计算资源,而且容易导致过拟合问题.近年来,研究者在网络模型压缩方面作了大量的工作[5 -7 ] ,Han等[8 ] 基于AlexNet[1 ] 和VGGNet[9 ] 实现了基于权重裁剪的算法,通过重新训练弥补准确率损失,该算法主要裁减全连接层的参数,而神经网络的计算消耗主要来自卷积层,所以该算法不能明显提升模型的计算效率. 为了降低卷积层的计算消耗,Iandola等[10 ] 实现了利用稀疏矩阵计算库和特殊硬件[11 ] 压缩卷积层的算法. Denil等[4 ] 实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
... 如图1 所示,在核矩阵A ${{{P}}_{i,j}}$ ${{{X}}_{i + 1}}$ B $\left( {{n_i}{h_{i + 1}}{w_{i + 1}}{\rm{ + }}{n_{i + 2}}{h_{i + 2}}{w_{i + 2}}} \right){k^2}$ [15 ] . 所以裁减掉第 $i$ $m$ $i$ $i{\rm{ + }}1$ $m/{n_{i + 1}}$ . ...
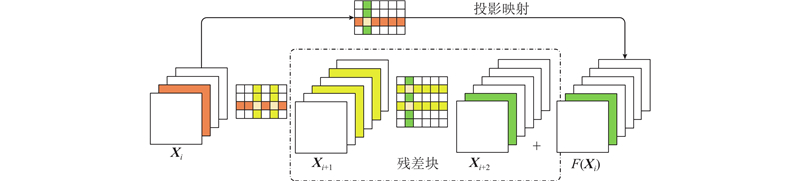
... 对于简单的卷积神经网络,如VGG或者AlexNet,可以较容易地裁减任意滤波器,但对于复杂网络,如ResNet,因为网络结构的特殊性,滤波器的裁剪受限于具体的网络层连接. 如图2 所示,通过投影映射(projection mapping)实现对残差块(residual block)的滤波器裁剪[15 ] . 其中裁剪的关键是每个残差块第2个卷积层的输出特征图与恒等特征图之间通道一致性的保持. 在裁剪残差块第2个卷积层的过程中,要同时裁减掉相应的投影特征图. 因为恒等映射比残差块更重要,残差块的裁剪由快捷层(shortcut layer)决定,残差块第2个卷积层特征图的裁剪需要与快捷层的裁剪所选择的滤波器索引一致. ...
... 2)基于L1范数的裁剪算法[15 ] :裁剪网络层中权重L1范数较小的滤波器来获得模型的性能提升. ...
2
... 多种深度学习模型已经证明存在着大量的参数冗余[4 ] ,带有冗余参数的模型不仅浪费存储空间和计算资源,而且容易导致过拟合问题.近年来,研究者在网络模型压缩方面作了大量的工作[5 -7 ] ,Han等[8 ] 基于AlexNet[1 ] 和VGGNet[9 ] 实现了基于权重裁剪的算法,通过重新训练弥补准确率损失,该算法主要裁减全连接层的参数,而神经网络的计算消耗主要来自卷积层,所以该算法不能明显提升模型的计算效率. 为了降低卷积层的计算消耗,Iandola等[10 ] 实现了利用稀疏矩阵计算库和特殊硬件[11 ] 压缩卷积层的算法. Denil等[4 ] 实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
... 3)Random Pruning[16 ] :对于每一个卷积层,随机裁剪一定量的滤波器来对模型进行压缩和加速. ...
1
... 多种深度学习模型已经证明存在着大量的参数冗余[4 ] ,带有冗余参数的模型不仅浪费存储空间和计算资源,而且容易导致过拟合问题.近年来,研究者在网络模型压缩方面作了大量的工作[5 -7 ] ,Han等[8 ] 基于AlexNet[1 ] 和VGGNet[9 ] 实现了基于权重裁剪的算法,通过重新训练弥补准确率损失,该算法主要裁减全连接层的参数,而神经网络的计算消耗主要来自卷积层,所以该算法不能明显提升模型的计算效率. 为了降低卷积层的计算消耗,Iandola等[10 ] 实现了利用稀疏矩阵计算库和特殊硬件[11 ] 压缩卷积层的算法. Denil等[4 ] 实现了将权重矩阵分解为2个较小矩阵低秩乘积的算法,用来近似卷积计算,提升网络性能. 此外,基于卷积的快速傅里叶变换[12 ] 、参数量化[8 ] 、参数二值化[13 ] 等方法相继被提出. 基于核的稀疏化方法也引起了很多研究者的兴趣,Wen等[14 ] 提出结构稀疏化算法,能够学习模型的稀疏结构实现模型加速,稀疏的结构性可以有效地在硬件上部署加速. 最近,基于通道裁剪的方法表现出了较好的性能.Li等[15 ] 实现了基于L1范数的冗余滤波器裁剪算法,通过微调(fine-tune)恢复模型精度. Mittal等[16 ] 验证了随机通道裁剪可以与各种更复杂的裁剪标准相媲美,展示了网络模型的可塑性. Zhu等[17 ] 通过实验表明,训练小密度模型不能达到与具有相同内存占用的大稀疏裁剪模型相同的精度,说明模型裁剪算法的研究具有一定的实用意义. ...
1
... 通过VGG和ResNet[18 ] 模型描述滤波器裁剪算法,这2种网络最具代表性,在很多任务中都有广泛应用,不限于目标分类和目标检测,尤其是ResNet的提出,对网络层数的加深具有重要的意义. ...
1
... VGG-16在CIFAR-10数据集上表现了出色的性能[19 ] ,这里的VGG-16包含了13个卷积层和2个全连接层,由于CIFAR-10数据集的输入图片尺寸较小,2个全连接层的权重不占用太多空间. Batch Normalization比丢弃法在解决训练和过拟合的问题上效果更好,故在VGG-16模型中的每个卷积层后增加了Batch Normalization层[20 ] . ...
1
... VGG-16在CIFAR-10数据集上表现了出色的性能[19 ] ,这里的VGG-16包含了13个卷积层和2个全连接层,由于CIFAR-10数据集的输入图片尺寸较小,2个全连接层的权重不占用太多空间. Batch Normalization比丢弃法在解决训练和过拟合的问题上效果更好,故在VGG-16模型中的每个卷积层后增加了Batch Normalization层[20 ] . ...
1
... 1)Average Percentage of Zeros(APoZ)[21 ] :通过裁减多数激活为0值的滤波器来降低模型大小和运算量. ...
1
... 4)Mean Activation[22 ] :通过裁减平均激活值较低的滤波器来提升网络性能. ...