近年来，随着中国西南地区工程用地的日渐紧张，许多储如电厂、变电站等大型建构筑物已“迁移”到山区. 在山区大面积施工的过程中，往往会形成大范围的混合料填方边坡，土石混合体（S-RM）的力学特性往往不同于均质土体或岩体，在工程中对剪切力学特性及损伤机理的研究对该类工程具有重大意义.

随着现代岩土力学的发展，众多学者对S-RM力学特性进行了相关研究. Lindquist等^[1-6]通过重塑样对S-RM力学特性进行相关研究. 虽然重塑模型便于室内实验的实施，但是其力学性能与原位岩土体不同. 为了避免上述缺点，油新华等^[7-12]采用现场水平推剪试验，研究S-RM宏观力学特性与变形，但目前尚未有学者对S-RM水平推剪细观损伤过程进行相关研究.

近年来，众多学者采用离散元（DEM），对S-RM细观损伤过程展开相应的研究. Alessandro 等^[13]采用DEM研究S-RM的力学特性，但未对剪切破坏过程进行深入探讨. 金磊等^[14]采用三维随机模型，分析S-RM剪切破坏过程中的微裂纹数目发展过程及裂纹扩展情况. Xu等^[15-16]对S-RM剪切变形破坏过程中的内部结构变化情况与剪切带形成过程作了深入的探讨. 徐文杰等^[17]通过颗粒位移与旋转特征分析S-RM剪切变形特征. Zhang等^[18]分析S-RM变形过程中的剪切带形成过程与块石运动情况. 何春灿等^[19]采用DEM研究块石破碎对S-RM力学特性的影响，但未对其细观损伤过程进行进一步的分析. 金磊等^[20]通过颗粒接触力与颗粒运动，从细观尺度上研究S-RM的变形破坏机制. 目前没有相关研究对S-RM微裂纹的组构特征进行定量分析. 在S-RM变形破坏过程中，研究微裂纹组构的演化特征对于揭示S-RM细观损伤机理尤为重要.

采用离散元数值模拟方法，结合现场水平推剪试验，开展S-RM水平推剪数值实验研究. 根据水平推力演化过程，对S-RM破坏过程进行初步阶段划分. 基于傅里叶近似法提出S-RM微裂纹各向异性特征定量评价方法，根据S-RM变形破坏过程中的微裂纹各向异性演化特征，进一步划分了S-RM水平推剪细观损伤阶段. 通过分析各细观损伤阶段的细观裂纹与宏观裂纹扩展特征及发展规律，揭示了S-RM剪切滑动面形成机理.

该研究区位于中国西南地区，为一±500 kV换流站. 如图1所示为现场填方区S-RM回填层，结合现场的实际开挖回填情况，回填料主要由含大量不同粒径块石的S-RM组成. 填土呈褐灰色、黄褐色，主要成分为砂土，混大量碎石、块石及角砾，碎石的主要成分为灰岩及泥质页岩，棱角状，粒径大小不等，最大块石粒径为80~120 mm.

土体与块石的主要物理力学指标如下：砂土天然密度为1.9 g/cm³，天然水质量分数为8%~30%，孔隙比为0.5~1.0，通过室内直剪实验得到砂土的黏聚力为8.5~23 kPa，内摩擦角为12°~16°；灰岩天然密度为2.9 g/cm³, 无侧限抗压强度为50 MPa.

现场填方边坡块石质量分数为30%~60%，在块石质量分数不同的区域，分别在干燥天气（水质量分数约为12%）与降雨时（水质量分数约为20%）各进行3组试验. 该次试验选取的场地主要含灰岩块石，块石粒径为5~120 mm. 现场水平试验尺寸为108 cm×66 cm×30 cm，试验装置如图2所示. 试样与装置准备就绪后分级施加水平推力，推力控制每级荷载在1 min左右完成，千斤顶油压表每1 MPa为一级. 每分钟记录一次百分表及压力表的读数，水平推力达到最大值P_max时记录相应的压力及位移；当水平推力急剧下降时停止加压，待压力稳定后重新开动加压，并记录下二次加压过程中所能达到的最大推力P_min. 试验结束后，清除滑动面以上滑体（见图3），通过测量得到滑面数据并绘制出二维平均滑动面，根据平均滑面划分条块计算S-RM力学参数. 根据林宗元^[21]提出的公式，可以分别计算得到S-RM的内摩擦角φ与黏聚力c：

(1) $\tan \varphi = \displaystyle\frac{{\displaystyle\frac{{{P_{\max}}}}{G}\displaystyle\sum\limits_{i = 1}^n {{g_i}\cos {\alpha _i} - \displaystyle\sum\limits_{i = 1}^n {{g_i}\sin {\alpha _i} - c\displaystyle\sum\limits_{{i} = {1}}^{n} {{{l}_{i}}} } } }}{{\displaystyle\frac{{{P_{\max}}}}{G}\displaystyle\sum\limits_{i = 1}^n {{g_i}\sin {\alpha _i} + \displaystyle\sum\limits_{i = 1}^n {{g_i}\cos {\alpha _i}} } }}.$

(2) ${{c}} = \frac{{{{{P}}_{\max}}{{ - }}{{{P}}_{\min}}}}{{\displaystyle\sum\limits_{{{i}} = {{1}}}^{{n}} {{{{l}}_{{i}}}} }}.$

式中：P_max为单位宽度最大水平推力，P_min为最小水平推力，G为单位宽度剪切体重力，g_i为各条块每单位宽度土的重力，α_i为第i条块滑动面与水平面夹角，l_i第i条块滑动线长度.

式（2）假设水平推剪试验第一次达到最大推力P_max时，S-RM黏聚力与摩擦力共同提供抗剪强度，而在滑动面形成后再次加压至P_min的过程中仅由摩擦力提供抗剪强度，故根据式（2）可以计算得到S-RM黏聚力，该假设适用于砂土-块石混合体. 根据计算得到的S-RM黏聚力与极限平衡法可知，假设S-RM达到P_max时S-RM处于极限平衡状态，依据受力平衡（见式（1））计算得到S-RM内摩擦角是合理的，故可以使用式（1）、（2）计算得到S-RM内摩擦角与黏聚力.

从现场试验得到的实验结果（见表1）可以看出，当S-RM水质量分数w_w相同时，随着块石质量分数w_r的增加，S-RM的黏聚力下降，内摩擦角增加，与徐文杰等^[9-12]研究得到的规律一致. 1~3号试样水质量分数约为11%，4~6号试样水质量分数约为20%，从实验结果可以看出，当w_r相近时，S-RM黏聚力与内摩擦角随着w_w的增加均有较大幅度的减小.

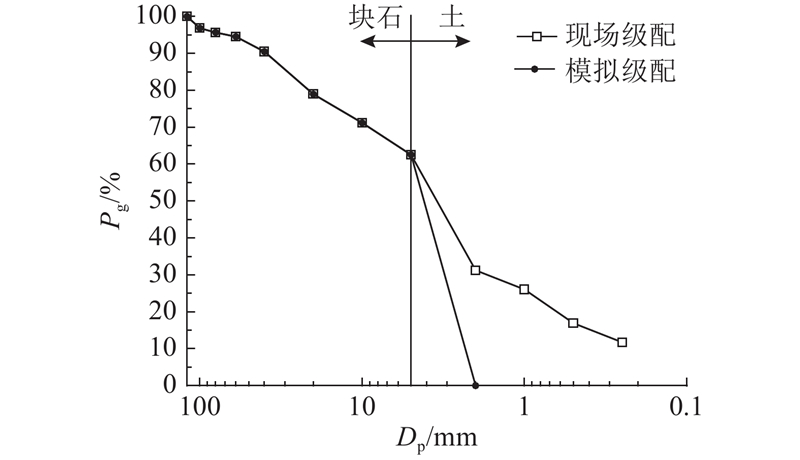
采用颗粒流离散元软件PFC^2D，对3号S-RM水平推剪损伤过程进行模拟计算. 通过数码相机得到现场不同粒径块石的原始照片（见图4（a）），经过裁剪，灰度处理，减噪，滤波，二值化图像分割与边缘识别等图像数字处理方法，可得不同粒径典型灰岩块石的二维截面形状（见图4（b））. 如图5所示为现场筛分后得到的累计级配曲线. 图中，D_p为颗粒粒径，P_d为小于某粒径的累计质量百分比. 考虑离散元软件的计算能力，采用等量替代法对离散元模拟时的颗粒级配曲线进行修正，建立数值模型时将小于2 mm的土颗粒粒径扩大统一为2 ~5 mm，使土颗粒粒径在2~5 mm内均匀分布，而块石级配与现场级配保持一致. S-RM的水平推剪数值模型如图6所示. 在现场试验中，w_r为37%，通过质量比与面积比的转换，得到数值模型中的块石面积所占百分比为30%. 其中粒径大于10 mm的块石形状与图4中典型块石的二维形状保持一致，粒径为5~10 mm的小块石统一采用粒径为5~10 mm的圆盘形状代替. 由于该二维数值模拟无法考虑三维块石真实形状与块石的真实分布情况，该数值试验结果不考虑真实块石形状的影响，各级配块石随机分布于数值模型中.

具体建模过程如下.

1)在模型尺寸范围内，根据不同粒径典型块石二维截面形状建立与块石形状一致的墙，在块石墙内随机分布粒径为4 mm的颗粒，计算一定步数至颗粒均匀且充分填充每个块石.

2)在略高于模型尺寸（高度为50 cm）的范围内，按照模拟设计级配（见图5）均匀生成粒径为5~10 mm的块石颗粒与2~5 mm的土体颗粒，计算一定时步至颗粒均匀填充模型.

3)删除所有块石墙体，赋予所有颗粒0.1的阻尼系数，赋予土体与块石颗粒相应的细观参数（见表1、2），施加重力加速度10 g/cm²，计算一定时步使模型在自重条件下达到平衡状态. 删除模型高度为45 cm以上的颗粒，使模型上表面平整.

根据灰岩的单轴抗压强度与模拟中选取的颗粒粒径，通过单轴抗压模拟试验反演出块石的细观参数（见表2）. 其中粒径为10~120 mm的块石采用平行黏结模型，将粒径为4 mm的颗粒黏结成典型块石形状；粒径为5~10 mm的块石采用线性接触模型，以粒径为5~10 mm的圆形颗粒代替. 采用接触黏结，将粒径为2~5 mm的圆形颗粒黏结为土体；根据现场试验结果，通过多次水平推剪数值试验，试算反演得到土颗粒对应的细观参数，如表2所示. 表中，块石粒径为d_block，颗粒粒径为D_p，接触弹性模量为E，刚度比为R_a，密度为ρ，法向黏结强度为S_n，切向黏结强度为S_s，黏结弹性模量为E_b，黏结刚度比为R_b，摩擦系数为f.

该场地为填方场地，块石与土体间无胶结现象，故块石与土体间采用线性接触模型. 块石与土体接触面细观参数通过多次数值试验反演得到，E=10 MPa，R_a=1.0，f=1.0.

在模型建立并赋予相应的土石参数后，给试验体左侧传力墙体赋予水平速度1 mm/s，对试验体进行推剪. 在试验过程中，监测传力墙体水平位移、颗粒作用于墙体的水平推力、孔隙率及摩擦能耗，在监测到水平推力到达P_min后即可停止试验.

在试验过程中，当颗粒之间的黏结在法向或切向受到超过法向黏结强度或切向黏结强度的作用力时，黏结发生断裂，此时一条微裂纹产生. 在数值试验过程中，对微裂纹的个数、破坏类型、位置及裂纹倾角进行监测. 在后续颗粒间的破坏分析中，由于块石与土体的接触假设为线性接触模型，没有考虑块石与土体之间微裂纹的产生.

在S-RM破坏阶段，微裂纹大量生成形成剪切滑动面，该阶段所表现出的细观损伤特性与微裂纹细观组构演化规律密切相关，Bathurst^[22]采用傅里叶级数近似表达离散颗粒材料的粒间接触方向分布特征，提出各向异性系数定量表达颗粒接触的各向异性程度. 傅里叶近似法已被Rothenburg等^[23-24]应用于离散材料粒间接触组构的各向异性研究中，现基于傅里叶近似法提出微裂纹各向异性定量评价方法.

每条微裂纹由中心位置、倾角方向及破坏类型来进行表征，在试验过程中，当颗粒之间的黏结在切向受到超过切向黏结强度的作用力时，黏结发生剪切断裂，此时生成的微裂纹破坏形式为剪切破坏；当颗粒之间的黏结在法向受到超过法向黏结强度的作用力，黏结发生拉断裂，此时生成的微裂纹破坏形式为拉伸破坏. 微裂纹的中心位置及倾角方向如图7所示. 假设2个颗粒间产生微裂纹时颗粒间距为2d，通过颗粒间距中心点与颗粒中心连线垂直的直线称为颗粒间距中心线. 微裂纹的中心位置为产生该裂纹的2个颗粒中心点连线与颗粒间距中心线的交点；微裂纹的倾角方向为水平方向逆时针旋转与颗粒间距中心线所成的角度，每条裂纹在[0°，360°]内存在2个倾角方向θ₁与θ₂，θ₂=θ₁+180°.

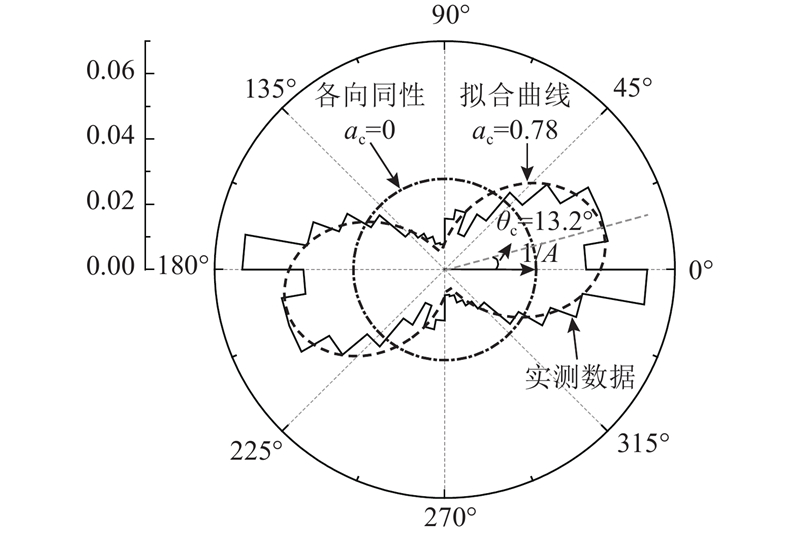
由于微裂纹倾角θ∈[0°，360°]，且θ=180°+θ，微裂纹倾角各向异性程度可以采用傅里叶近似法分析：统计等裂纹倾角间隔内（取10°为一个间隔）的裂纹个数l，由于统计裂纹时每条裂纹被统计2次，裂纹统计总个数为2L，将裂纹倾角间隔内裂纹个数占比l/（2L）与θ的关系绘制成极坐标曲线，根据下式拟合分析微裂纹的各向异性特征：

(3) $E\left( \theta \right) = \frac{1}{A}\left[ {1 + {a_{\rm c}}\cos \left (2(\theta - {\theta _{\rm c}})\frac{\pi }{{180}} \right )}\right].$

式中：E（θ）为微裂纹倾角分布函数；a_c为微裂纹倾角方向各向异性系数，a_c越大各向异性程度越大，当a_c=0时代表各向同性；A为拟合系数，是各向同性时每裂纹倾角间隔内裂纹个数占比，即各向同性圆的半径大小（见图8），由于在[0°，360°]划分了36个倾角间隔，A为36；θ为裂纹倾角；θ_c为裂纹倾角主方向，单位为°；当θ=θ_c或θ_c+180°时，E（θ）最大；当θ=θ_c+90°或θ_c+270°时，E（θ）最小. 如图8所示为数值试验中滑动面完全形成时的微裂纹倾角分布图及拟合曲线，使用傅里叶近似法得到的拟合曲线R²=0.88.

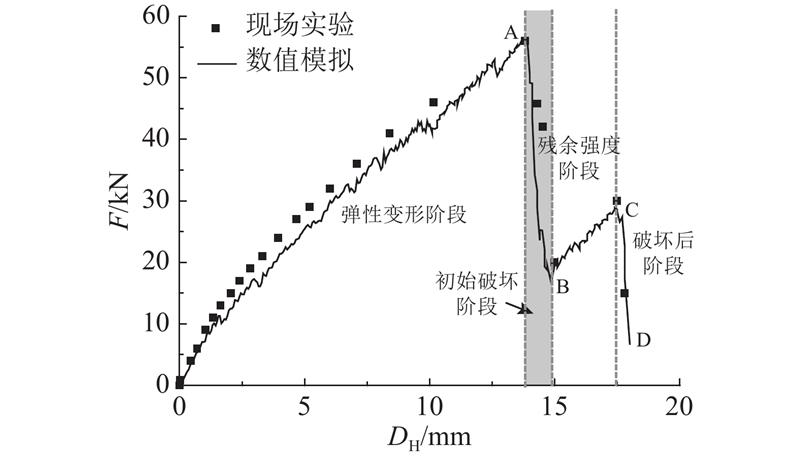
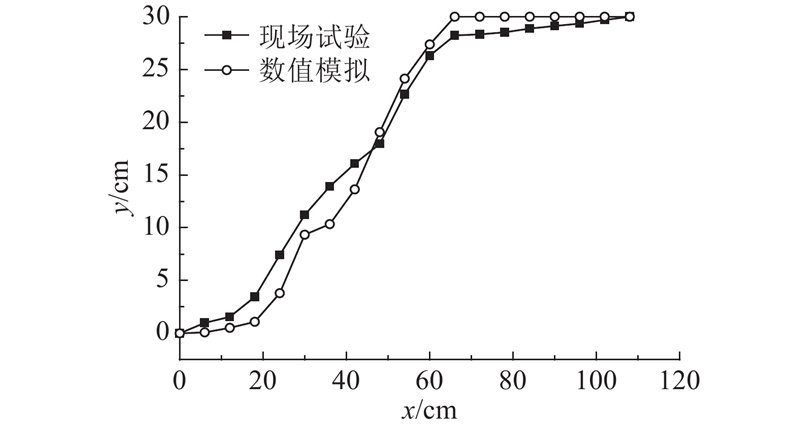
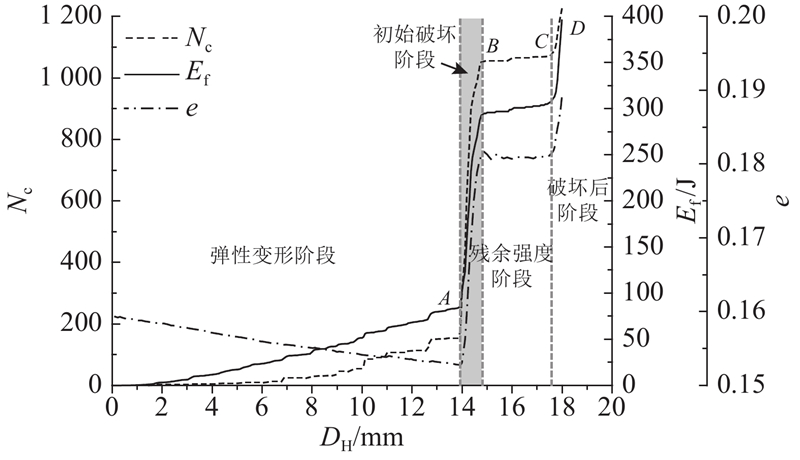
数值模拟结果如图9所示. 图中，剪切位移为D_H，水平推力为F，其中P_max取A点水平推力，P_min取B点水平推力（最大残余推力）. 对比现场试验结果可知数值试验中水平推力随剪切位移的发展过程，P_max与P_min均与现场试验基本一致，说明数值模型中采用的细观参数可以合理地反映该岩土体的力学性能. 如图10所示为水平推剪滑动面. 图中，x为水平方向坐标，y为滑动面高度坐标. 将3#水平推剪滑动面平均剖面与数值试验得到的二维滑动面进行对比，通过现场试验得到的平均滑动面在水平坐标66 cm处没有完全剪出，与模拟得到的结果有差异，这是由于现场块石分布不均匀所致，3号试验滑动面约2/3的区域在水平坐标66 cm处剪出，约1/3的区域在水平坐标108 cm处剪出. 从现场试验平均滑动面可以看出，滑面在水平坐标66 cm处有一明显拐点，且66~108 cm区间滑面与地表仅有不到2 cm左右的高度，可以认为滑动体整体从66 cm处剪出，故该模拟可以合理地反映现场试验过程.

根据F的演化过程（见图9），将水平推剪过程划分为4个阶段：压缩阶段、初始破坏阶段、残余强度阶段与破坏后阶段. 其中每个阶段的水平推力、细观结构及能量演化规律如图9、11所示. 图中， N _c为微裂纹数，E _f为摩擦能耗，e为孔隙率.

1)压缩阶段（OA段）：试样孔隙率随着D_H的增加而线性减小，说明该阶段岩土体随着D_H的增加逐渐压缩；F随着D_H的增长而增长，但F增长速率随着D_H的增长呈现减小的趋势，说明该阶段S-RM以弹性变形为主，但存在一定程度的塑性变形；N_c随着D_H的增加而缓慢增加，当D_H达到A点时，N_c较少且零散分布于岩土体中，没有明显的贯穿裂纹产生，说明该阶段岩土体已经发生一定程度的塑性变形但未发生明显破坏；E_f随着D_H的增加而缓慢增加，且增长速率逐渐加快，这是由于随着剪切位移的增加土体中有更多的微裂纹生成，土体颗粒间滑动产生的E_f逐渐增多，且随着剪切位移的增加，土体与块石间存在一定的相对运动，也会产生一部分E_f.

2)初始破坏阶段（AB段）：F随着D_H急速下降，同时n急剧上升，这是由于在初始破坏阶段微裂纹沿滑动面快速发展直至贯穿岩土体，此时滑动面完全形成. E_f在破坏阶段急剧上升，这是由于岩土体在产生裂纹后发生相对位移所致.

3)残余强度阶段（BC段）：F在初始破坏阶段下降后有所增加，此时n呈现缓慢下降的趋势，E_f呈现缓慢上升的趋势，而微裂纹停止发展，这是由于岩土体在F的作用下再次被压实，岩土体沿着滑动面发生滑移，此时岩土体的强度仅由摩擦力提供，表现出破坏后最大残余强度.

4)破坏后阶段（CD段）：在CD段F再次急剧下降，n、N_c与E_f再次急剧上升，这是由于岩土体在完全破坏后随着水平位移的增加发生进一步挤压局部破坏.

根据初始破坏阶段的微裂纹各向异性特征发展过程，将初始破坏阶段微裂纹演化过程划分为4个细观损伤阶段（见图12）：裂纹初始发展阶段、裂纹扩展阶段、主裂纹形成阶段与滑动面形成阶段. 将微裂纹倾角分为4个区间：f_r1（0°~45°），f_r2（45°~90°），f_r3（90°~135°），f_r4（135°~180°），分析各演化阶段的微裂纹各向异性演化特征.

1)裂纹初始发展阶段（A-A₁段）：当剪切位移到达A点时，由于微裂纹零散分布在岩土体内，此时微裂纹各向异性程度较弱，微裂纹主要分布在f_r1与f_r2区（见图13（a））. 该阶段随着裂纹的迅速增长，a_c先迅速增加而后增长速率逐渐减小，说明随着剪切位移的增加，微裂纹各向异性程度逐渐增强. θ_c随着剪切位移的增加而快速减小，当剪切位移到达A₁点时微裂纹主要分布在f_r1与f_r4区（见图13（b））.

2)裂纹扩展阶段（A₁-A₂段）：该阶段a_c再次快速增长，各向异性程度增强. θ_c在该阶段继续快速减小，该阶段微裂纹在f_r4区有显著增加（见图13（c））.

3)主裂纹形成阶段（A₂-A₃段）：该阶段a_c随着剪切位移的增加而快速增长，各向异性程度继续增强，但a_c的增长速率小于裂纹扩展阶段. θ_c在该阶段呈现缓慢增长的趋势，该阶段微裂纹在f_r1区有显著增加（见图13（d））.

4)滑动面形成阶段（A₃-B段）：该阶段a_c与θ_c随着剪切位移的增加均呈现减小的趋势，但基本趋于稳定，不再有显著变化，说明此时滑动面已基本形成. 当位移到达B点时，微裂纹主要分布于f_r1与f_r4区，各向异性显著（见图13（e））.

微裂纹的破坏类型有2种：破坏类型为拉伸破坏的微裂纹称为拉裂纹，破坏形式为剪切破坏的微裂纹称为剪切裂纹. 通过统计初始破坏阶段的拉裂纹与剪切裂纹数目、裂纹比f_ts（拉裂纹数目/剪切裂纹数目）与各向异性系数（见图14），结合不同倾角区间裂纹发展过程（见图15），分析拉裂纹与剪切裂纹在不同细观损伤阶段的演化规律. 图中，a_ct为拉裂纹各向异性系数.

在初始破坏阶段，拉裂纹与剪切裂纹增长速率逐渐变小最终趋于稳定；微裂纹的产生主要由于颗粒间的拉应力导致；拉裂纹的各向异性程度大于剪切裂纹（见图14）.

1)裂纹初始发展阶段（A-A₁段）：该阶段拉裂纹与剪切裂纹数目随着剪切位移的增加呈线性增长，f_ts从1.25增长至1.5，说明在裂纹初始发展阶段，拉裂纹的增长速率大于剪切裂纹（见图14）. a_ct随着剪切位移的增加有明显增加，a_cs没有明显增长，这是由于该阶段拉裂纹在f_r1区的增长明显大于其他区域，剪切裂纹在各倾角区间内的增长较均匀（见图15）.

2)裂纹扩展阶段（A₁-A₂段）：该阶段拉裂纹与剪切裂纹数目随着剪切位移的增加呈线性增长，f_ts继续增长，说明在该阶段的拉裂纹增长速率大于剪切裂纹（见图14）. a_ct随着剪切位移的增加而增长，但增长速率明显低于裂纹初始发展阶段，a_cs无明显增长；当剪切位移到达A₂点时，拉裂纹主要分布于f_r1区与f_r4区，剪切裂纹在f_r1区，f_r2区与f_r4区内均匀分布（见图15）.

3)主裂纹形成阶段（A₂-A₃段）：该阶段剪切裂纹数目随着剪切位移的增加呈线性增长，拉裂纹增长速率逐渐减缓，f_ts先增长后减小，说明在该阶段的剪切裂纹增长速率逐渐大于拉裂纹（见图14）. a_ct随着剪切位移的增加有缓慢增长， a_cs快速增长，这是由于在该阶段，剪切裂纹大量产生于f_r1区（见图15）.

4)滑动面形成阶段（A₃-B段）：该阶段剪切裂纹数目与拉裂纹数目随着剪切位移的增加而缓慢增长但趋于稳定，a_ct与a_cs无明显变化（见图14），说明在该阶段，主裂纹已形成，岩土体无进一步的明显破坏，岩土体随主裂纹产生滑移形成剪切滑动面. 当剪切位移达到B点时，拉裂纹各向异性程度明显大于剪切裂纹，拉裂纹集中分布于f_r1区与f_r4区，剪切裂纹在f_r1区，f_r2区与f_r4区内均匀分布（见图15）.

统计微裂纹分别在f_r1区与f_r2区、f_r3区与f_r4区的平均倾角角度f_mean12与f_mean34，分析裂纹倾角在不同细观损伤阶段的演化规律，结合宏观裂纹发展过程（见图16、17）揭示S-RM滑动面的形成机理. 图17中，黑色实线为微裂纹，黑色虚线为宏观裂纹.

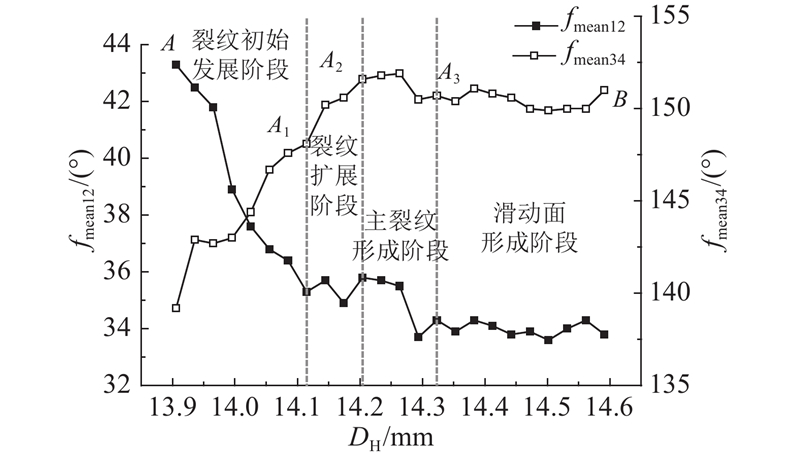
1)裂纹初始发展阶段（A-A₁段）：该阶段随着剪切位移的增加，f_mean12快速减小，f_mean34快速增大. 当剪切位移到达A₁点时，岩土体中出现零散的微裂纹，一条宏观裂纹从传力墙体底部沿水平方向扩展（见图17（a））.

2)裂纹扩展阶段（A₁-A₂段）：该阶段的f_mean34随着剪切位移的增加而快速增大，f_mean12无明显变化，这是由于该阶段产生的微裂纹主要分布在f_r4区. 宏观裂纹在块石之间的土体中快速扩展，逐渐延伸至剪出口位置. 当剪切位移成几条倾角不同的宏观裂纹，此时宏观裂纹倾角方向为30°~41°（见图17（b））.

3)主裂纹形成阶段（A₂-A₃段）：该阶段f_mean12有明显的减小，f_mean34的变化幅度较前一阶段有所减小，这是由于该阶段产生的微裂纹主要分布在f_r1区. 在水平推剪破坏过程中，与水平推力方向逆时针角度呈锐角的宏观裂纹称为主裂纹，反之称为次生裂纹. 随着剪切位移的继续增长与块石的翻转，土体中的宏观裂纹进一步发展逐渐相连形成一条绕过块石的主裂纹. 当剪切位移到达A₃点时，一条贯通岩土体的主裂纹形成，主裂纹的倾角为34°，与此时的f_mean12基本一致. 同时，若干条次生裂纹从主裂纹上沿着相反的方向发展，次生裂纹的倾角为143°~148°（见图17（c））.

4)滑动面形成阶段（A₃-B段）：该阶段f_mean12与f_mean34均无明显变化，f_mean12稳定在34°左右，f_mean34稳定在151°左右. 随着剪切位移的持续增加，岩土体沿着主裂纹发生相对滑动，形成绕石剪切滑动面. 当剪切位移到达B点时，滑动面上、下岩土体已存在明显的分离（见图17（d）），此时滑动面的倾角为34°，与主裂纹倾角和f_mean12一致.

(1)根据F的演化过程将水平推剪过程划分为4个阶段：压缩阶段、初始破坏阶段、残余强度阶段与破坏后阶段. 在初始破坏阶段，微裂纹沿滑动面快速发展直至贯穿岩土体，此时滑动面完全形成.

(2)基于傅里叶近似法，提出S-RM微裂纹各向异性特征定量评价方法. 根据S-RM变形破坏过程中的微裂纹各向异性演化特征，进一步划分了S-RM水平推剪细观损伤阶段：裂纹初始发展阶段、裂纹扩展阶段、主裂纹形成阶段与滑动面形成阶段. 微裂纹各向异性程度随着剪切位移的增加而增长，当主裂纹形成后不再有明显变化，微裂纹主要分布于f_r1与f_r4区.

(3)在初始破坏阶段，拉裂纹与剪切裂纹的增长速率逐渐变小最终趋于稳定，微裂纹的产生主要由于颗粒间的拉应力导致. 拉裂纹各向异性拉裂纹的各向异性程度明显大于剪切裂纹，其中拉裂纹集中分布于f_r1区与f_r4区，剪切裂纹在f_r1区、f_r2区与f_r4区内均匀分布.

(4)微裂纹在块石间土体中贯通形成多条宏观裂纹，随着剪切位移的继续增长与块石的翻转，土体中的宏观裂纹进一步发展逐渐相连形成一条绕过块石的主裂纹，岩土体沿着主裂纹发生相对滑动，最终形成绕石剪切滑动面. 滑动面的倾角为34°，与主裂纹倾角一致，也与f_mean12一致.