浙江大学学报(工学版)

浙江大学学报(工学版), 2019, 53(10): 1927-1935 doi: 10.3785/j.issn.1008-973X.2019.10.010

土木工程

泡沫混凝土填充圆钢管的轴压力学性能

支旭东,, 郭梦慧,, 王臣, 武启剑

Mechanical properties of circular steel tube filled withfoam concrete under axial loads

ZHI Xu-dong,, GUO Meng-hui,, WANG Chen, WU Qi-jian

收稿日期: 2018-08-28  

Received: 2018-08-28  

作者简介 About authors

支旭东(1977—)，男，教授，博导，从事大跨空间结构的研究.orcid.org/0000-0002-4750-5642.E-mail:zhixudong@hit.edu.cn , E-mail：zhixudong@hit.edu.cn

摘要

采用试验和有限元模拟方法，研究泡沫混凝土填充圆钢管构件在轴压荷载作用下的力学性能. 通过轴压试验，分析短柱构件的耗能能力和长柱构件的轴压承载力，短柱构件发生叠缩破坏变形模式，耗能能力随着泡沫混凝土密度的提高而显著增强，长柱构件发生整体失稳破坏，稳定承载力随着泡沫混凝土密度的增大而增大. 基于ABAQUS的Explicit求解器，建立泡沫混凝土填充圆钢管构件的数值模型，获得的模拟结果与试验结果吻合良好. 开展参数分析，讨论径厚比、长细比及填充泡沫混凝土密度等因素对长柱构件承载能力的影响. 研究结果表明：长柱构件的稳定承载力随着长细比和径厚比的增大而减小，随着填充的泡沫混凝土密度的增大而增大. 基于Perry-Robertson公式，推导了泡沫混凝土填充圆钢管长柱构件的稳定承载力公式. 预测结果表明，该公式能够很好地预测长柱构件的稳定承载力.

关键词： 泡沫混凝土 ; 圆钢管 ; 轴压 ; 稳定性 ; Perry-Robertson

Abstract

The mechanical property of circular steel tube filled with foam concrete under axially compressive loads was analyzed with both experimental and numerical methods. The energy dissipation capacity of short column members and the axial load bearing capacity of long column members were analyzed by axial compressive experiments. Results showed that short column members failed with progressive folding and energy dissipation increased with the increase of foam concrete density. In the case of long column members, the overall instability failure occured, and the stable bearing capacity increased with the increase of foam concrete density. A numerical model based on ABAQUS Explicit solver was proposed, and the simulation results agreed well with the experimental results. The effects of foam concrete density, diameter-to-thickness ratio and slenderness ratio to specimen’s bearing capacity were analyzed. Results showed that the bearing capacity of long column members decreased with the increase of the diameter-to-thickness ratio and slenderness ratio, while increased with the increase of density of the filled foam concrete. A formula of stability capacity of long column members was derived based on the Perry-Robertson formula. The calculation results of the formula show that this formula can predict the axial load bearing capacity of long column members well.

Keywords： foam concrete ; circular steel tube ; axial loaded ; stability ; Perry-Robertson

PDF (3259KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

支旭东, 郭梦慧, 王臣, 武启剑. 泡沫混凝土填充圆钢管的轴压力学性能. 浙江大学学报(工学版)[J], 2019, 53(10): 1927-1935 doi:10.3785/j.issn.1008-973X.2019.10.010

ZHI Xu-dong, GUO Meng-hui, WANG Chen, WU Qi-jian. Mechanical properties of circular steel tube filled withfoam concrete under axial loads. Journal of Zhejiang University(Engineering Science)[J], 2019, 53(10): 1927-1935 doi:10.3785/j.issn.1008-973X.2019.10.010

泡沫材料填充构件因其独特的构造形式，相对于传统的泡沫材料和薄壁金属管件有更多的性能优势，如质量轻、比强度高、阻尼大、比吸能大等，因而在汽车制造和航空航天领域都已获得了广泛的应用[1-2].Baroutaji等[3-9]对泡沫材料填充构件的大量研究表明，内部填充轻质泡沫材料的金属管吸能体系由于泡沫材料和金属管之间的相互作用效应，吸能能力相对于单纯的金属管和泡沫有较大幅度的提升. Reid等[10]研究聚氨酯泡沫填充薄壁方管和矩形管的轴压稳定性和能量吸收性能，提出泡沫材料和薄壁管之间相互作用的理论模型. 桂良进等[11]建立泡沫填充圆柱壳在准静态轴向压缩荷载作用下的吸能特性分析模型，分析材料参数、几何参数对比吸能的影响，发现泡沫材料的相对密度对比吸能有显著的影响. 程涛等[12]利用LS-DYNA，分析泡沫铝填充多棱管在准静态压缩荷载下的变形模式和破坏机理. 为了获得良好的吸能性能，这些前期研究的填充材料多采用金属泡沫，如泡沫铝，但高昂的造价使金属泡沫难以应用在量大面广的土木工程领域中，与金属泡沫相比，泡沫混凝土价格低廉，且因质轻、多孔的特性，在保温和隔音领域有着广泛的应用. 随着军事防护工程[13-15]、飞机道面阻拦系统[16]及地下工程抗震防护领域的发展，泡沫混凝土的吸能性能逐渐受到重视.

以泡沫混凝土作为填充物的复合构件尚未有研究报道，本文提出泡沫混凝土填充圆钢管构件的复合构件形式，开展4根短柱和8根长柱构件的轴压试验. 通过对试件变形模式、荷载-轴向位移曲线的分析，结合有限元数值模拟，总结长细比、厚径比及泡沫混凝土密度等因素对泡沫混凝土填充圆钢管构件轴压力学性能的影响. 基于Perry-Robertson公式，推导出泡沫混凝土填充圆钢管长柱构件的稳定承载力公式.

1. 轴压试验方案

1.1. 试件制备

Bardi等[17-18]对大径厚比短柱薄壁壳体构件的研究表明，构件的极限应变正比于（D/t）2/m3（其中D/t为径厚比，m为环向波数），构件的极限应变与构件的屈曲模式直接相关. 在进行构件设计时，采用100、900和1 200 mm 3种长度尺寸，圆钢管的外径均为58 mm，厚度采用1和2 mm两种尺寸，从而径厚比分为58和29两种. 内部填充的泡沫混凝土，参考已有的对于泡沫混凝土的研究[19]，选用快硬硫铝酸盐水泥和动物蛋白发泡剂，设计密度等级为500和900 kg/m3的配合比，如表1所示. 表中，ρ为密度.

表 1   泡沫混凝土配合比

Tab.1  Mix proportion of foam concrete

ρ/(kg·m−3) m(水泥)/g m(水)/g m(泡沫)/g m(减水剂)/g
500 2 500 475 92.96 15
900 3 500 666.67 80.11 22.22

新窗口打开| 下载CSV


在制备试件时，首先对空钢管的端部进行打磨并对其中一端进行封口处理，随后进行泡沫混凝土浆体的配制，灌浆完毕后将试件的另一端进行封口处理，最后对构件进行蒸汽养护，发泡完成的构件如图1所示. 试件的主要参数如表2所示. 表中，以FS1-100-500为例说明各符号的含义，FS1表示钢管壁厚为1.0 mm的泡沫混凝土填充圆钢管，100表示试件长度为100 mm，500表示填充泡沫混凝土密度为500 kg/m3，λ为长柱构件的长细比.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   泡沫混凝土填充圆钢管截面

Fig.1   Cross section of circular steel tube filled with foam concrete


表 2   泡沫混凝土填充圆钢管试件的几何参数

Tab.2  Geometric parameters of circular steel tube filled with foam concrete

编号 ρ/(kg·m−3) D/t λ
FS1-100-500 500 58 −
FS1-100-900 900 58 −
FS2-100-500 500 29 −
FS2-100-900 900 29 −
FS1-900-500 500 58 44.65
FS1-900-900 900 58 44.65
FS1-1200-500 500 58 59.54
FS1-1200-900 900 58 59.54
FS2-900-500 500 29 45.43
FS2-900-900 900 29 45.43
FS2-1200-500 500 29 60.57
FS2-1200-900 900 29 60.57

新窗口打开| 下载CSV


1.2. 泡沫混凝土和钢管的材性试验

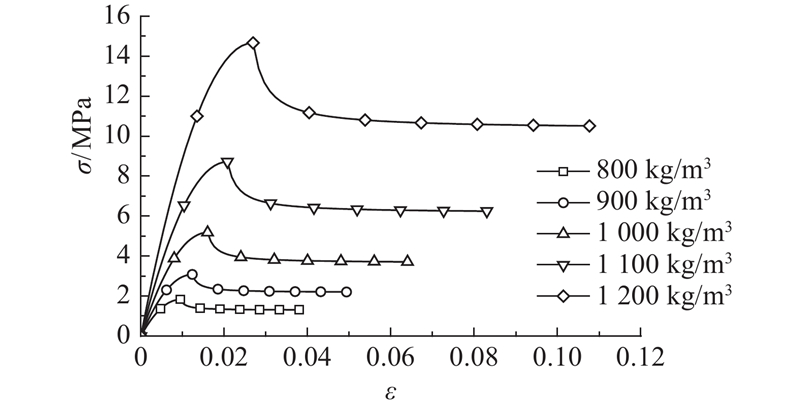
研究的泡沫混凝土填充圆钢管构件由外部薄壁Q235B直缝圆钢管和内部填充的泡沫混凝土共同组成. 在开展轴压试验前，首先开展2种材料的材性实验. 钢管材性试样的取样和静力拉伸试验依据GB/T 228-2010[20]和GB/T 2975-1998[21]的要求进行，拉伸速率取2 mm/min，得到的钢管材料性能参数如表3所示. 表中，t为壁厚，σy为屈服强度，σu为极限强度，Es为钢管的弹性模量，εu为断裂应变. 泡沫混凝土的材性试块按JG/T 266-2011[22]的要求设计为100 mm×100 mm×100 mm的标准立方体块，开展轴压实验，得到材料性能数据，如表4所示. 表中，ρo为设计密度，ρ为实测密度，fc为抗压强度，Ef为泡沫混凝土的弹性模量.

表 3   钢管的材料性能

Tab.3  Material parameters of steel tube

t/mm σy /MPa σu /MPa Es /GPa εu
1 326.78 504.80 196 0.181
2 255.77 431.01 201 0.182

新窗口打开| 下载CSV


表 4   泡沫混凝土的材料性能

Tab.4  Material parameters of foam concrete

ρo /(kg·m−3) ρ /(kg·m−3) fc /MPa Ef /MPa
500 500 1.02 270
900 851 3.08 417

新窗口打开| 下载CSV


1.3. 短柱轴压试验方案

短柱试件的轴压试验在哈尔滨工业大学结构与抗震实验中心开展. 在试验过程中，为了对试件进行有效约束，采用α-高强石膏将试件锚固在刚性方槽里. 试验装置如图2所示，通过油压千斤顶配合反力梁进行加载，加载速率选用10 kN/min，在底部加载端板位置处设置4个纵向的位移计，取4个位移计的平均值作为中心轴压短柱的轴向位移. 在试件安装时，采用激光水准仪进行对中，保证试件竖直不偏心.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   短柱试件加载装置

Fig.2   Loading device for short column specimens


1.4. 长柱轴压试验介绍

长柱试件两端采用双刀铰模拟铰支支座，刀铰与长柱试件之间采用α-高强石膏连接锚固. 长柱试件轴压加载装置如图3所示，在底部加载端板四角位置竖直方向及构件中部相互垂直的4个水平方向各设置一个位移计，以测量长柱试件的竖向位移和跨中侧向位移. 在长柱试件的中部对称布置4组相互垂直的应变片，两端对称布置4个应变片. 安装试件时使用激光水准仪进行对中，正式加载前先进行预加载消除虚位移的影响，采用10 kN/min的速度匀速加载.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   长柱试件加载

Fig.3   Loading device for long column specimens


2. 轴压试验结果

2.1. 短柱轴压试验结果

泡沫混凝土填充薄壁圆钢管短柱试件的典型破坏模式如图4所示. 不同壁厚试件的根部位置均发生了渐进的叠缩变形破坏，当径厚比较大（1 mm试件）时发生了非对称的叠缩破坏，当径厚比较小（2 mm试件）时发生了对称的叠缩破坏，叠缩模式主要与钢管的缺陷相关[23]，径厚比越大，即钢管越薄，存在的缺陷相对越显著，叠缩更趋于非对称叠缩. 在一些非结构的防护构件中，短柱构件的这种渐进叠缩破坏十分有利于消耗外界能量，进而保护主体结构. 对于泡沫混凝土填充圆钢管短柱构件，重点考察轴向荷载作用下的荷载-位移关系.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   短柱试件的破坏形态

Fig.4   Failure modes of short column specimens


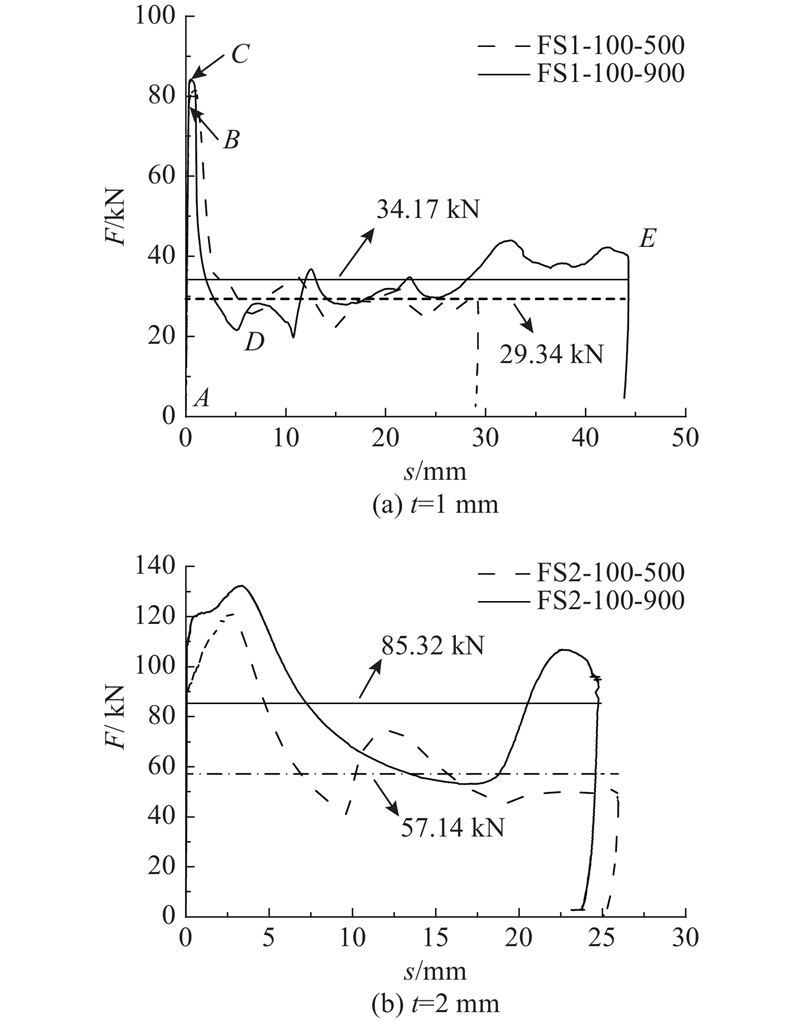
如图5所示为短柱试件在轴压荷载作用下的荷载F-位移s曲线. 结合短柱试件的变形模式可以将其轴压过程分为4个阶段，以FS1-100-900为例，如图5（a）所示. 1）弹性段（AB），该阶段钢管未发生屈服，整体变形小，荷载上升快，荷载的主要部分由钢管承担；2）塑性强化段（BC），随着钢管的逐渐屈服，荷载-位移曲线的斜率立刻减小，直至极限荷载；3）荷载下降段（CD），随着变形的继续增大，钢管在叠缩过程中形成环形三塑性铰[23]，构件的刚度迅速减小，承载力降低；4）荷载波动段（DE），轴向位移继续发展，第一个叠缩褶皱完成，并且内部填充的泡沫混凝土逐渐压溃、密实，构件的整体刚度再次增大，荷载-位移曲线开始随着叠缩变形波动.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   短柱试件轴向荷载-位移曲线

Fig.5   Axial load-displacement curves of short column specimens


在荷载波动段，以荷载-位移曲线与坐标轴围成的面积除以波动段的总位移，可得短柱试件在叠缩过程中的轴向平均压缩荷载Fm，Fm表征了短柱构件在叠缩过程中的耗能能力. Fm的计算公式为

$ {F_{\rm m}} = \frac{{\int_0^\varDelta {F{\rm d}s} }}{\varDelta }. $

式中：Δ为轴压总位移.

如图5的水平线所示，随着填充密度的增加，1 mm壁厚和2 mm壁厚的短柱试件的Fm分别提高了16.46%和49.31%，填充泡沫混凝土密度的提高明显增强了短柱构件的轴压耗能能力.

2.2. 长柱轴压试验结果

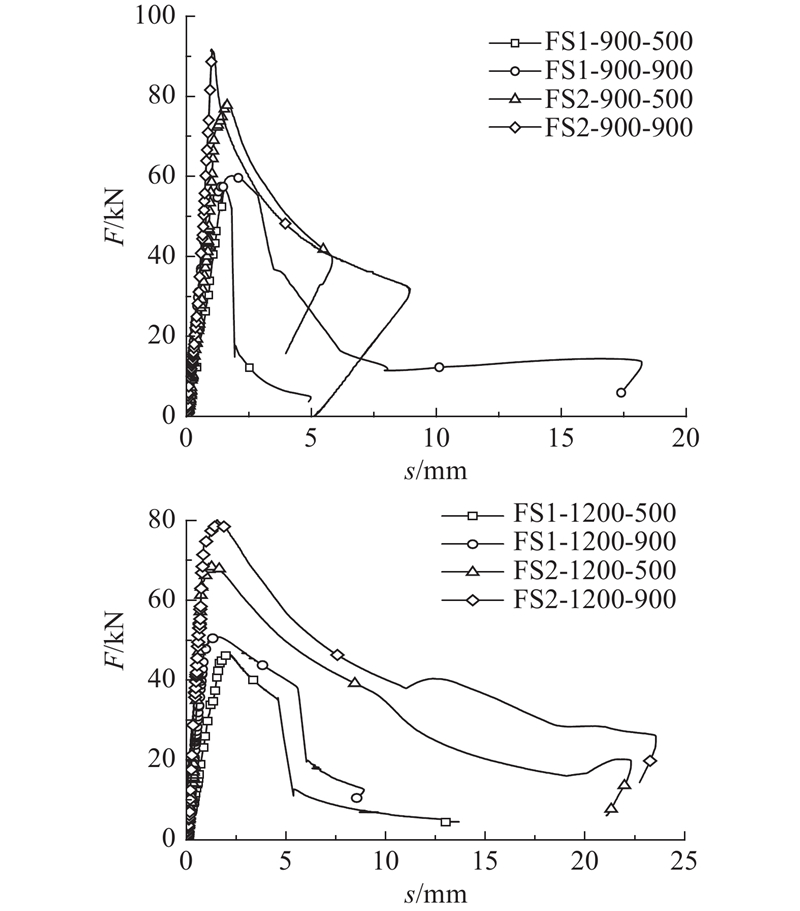
长柱试件的破坏模式如图6（a）所示，所有试件均发生了整体失稳破坏，在试件跨中位置发生了弯折. 长柱试件的轴向荷载-位移曲线如图7所示. 随着填充泡沫混凝土密度的提高及钢管壁厚的增大，试件的稳定承载力提高.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   长柱试件的破坏形态

Fig.6   Failure modes of long column specimens


图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   长柱试件轴向荷载-位移曲线

Fig.7   Axial load-displacement curves of long column specimens


3. 有限元模拟

3.1. 有限元模型

泡沫混凝土填充圆钢管构件的轴压过程中存在泡沫混凝土与钢管壁的接触以及存在钢材的叠缩，期间涉及到材料和几何的非线性，隐式算法一般难以收敛，故选用ABAQUS的Explicit求解器进行轴压试验的有限元模拟. 如图8所示的有限元模型，钢材和泡沫混凝土均选用8节点线性缩减积分实体单元（C3D8R）. 为了模拟短柱构件的叠缩变形，对短柱构件的网格进行细划，钢管的网格尺寸为1 mm，在钢管壁厚方向网格划分为3层，泡沫混凝土的网格尺寸为3 mm. 长柱构件由于发生整体失稳，计算时对网格精度的要求较低，故长柱构件的钢管网格尺寸设置为2 mm，混凝土网格尺寸均设置为5 mm，钢管壁厚方向仅划分为1层. 钢管材料模型选用多段塑性模型，泡沫混凝土的材料本构采用ABAQUS中的CRUSHABLE FOAM模型，硬化模型选用体积硬化（volumetric hardening）. 轴压分析时，通过关键字*IMPERFECTION添加一阶特征值屈曲形式的初始缺陷. 钢管与泡沫混凝土之间的接触切向为罚函数形式的摩擦接触，摩擦系数为0.2，法向为硬接触.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   泡沫混凝土填充薄壁圆钢管有限元模型

Fig.8   Finite element model of circular steel tube filled with foam concrete


3.2. 数值方法验证

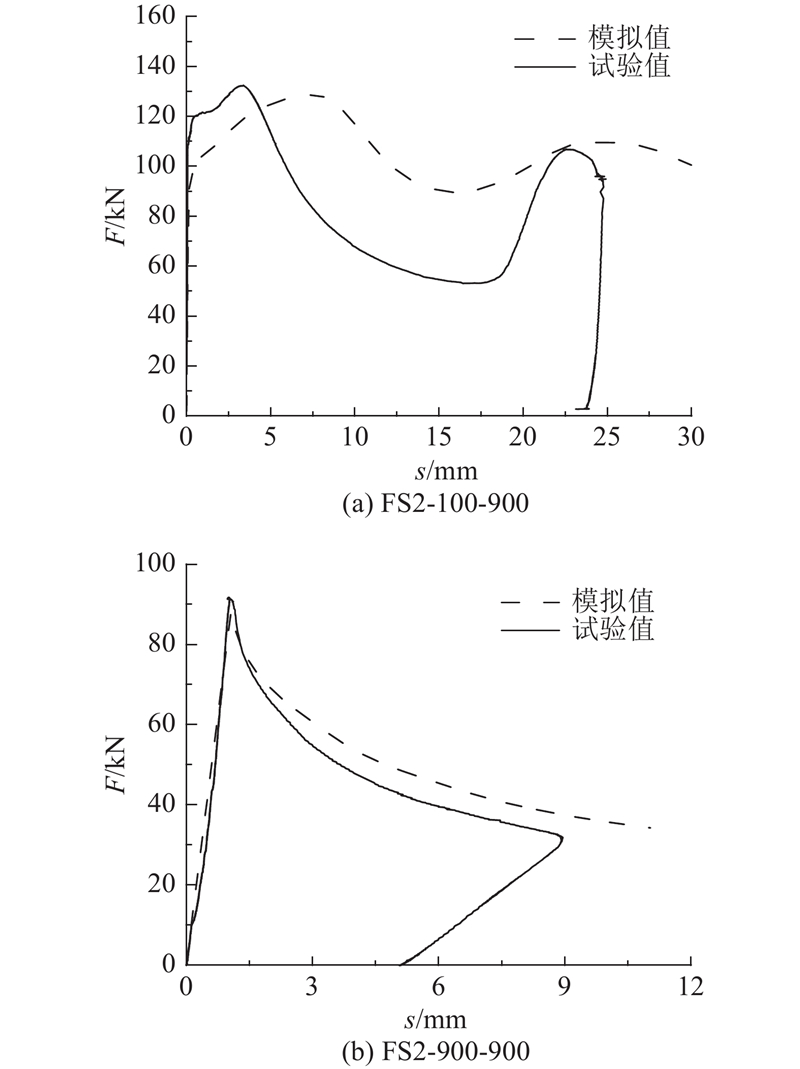
为了验证数值模型的正确性，以FS2-100-900和FS2-900-900两个试件为例，将数值计算后得到的试件变形和轴压荷载-位移曲线与试验结果对比分析，以验证有限元模型的正确性.

短柱试件根部发生均匀的叠缩变形，长柱试件发生失稳破坏，跨中弯曲. 数值模拟结果与试验现象吻合良好，如图9所示. 短柱试件的轴压荷载-位移曲线如图10（a）所示. 可以看出，模拟结果与试验结果在弹性段曲线吻合良好，而在钢管开始发生叠缩变形之后，模拟结果与试验结果出现了较大偏差，这是由于在叠缩阶段泡沫混凝土的压溃和接触方式发生改变引起的强烈非线性造成的. 对于长柱试件，由于发生的是整体失稳，通过数值模拟得到的轴压荷载-位移曲线与试验结果一致，如图10（b）所示.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   数值模拟与试验变形对比

Fig.9   Comparision of deformation between numerical and experimental results


图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   数值模拟与试验荷载-位移曲线对比

Fig.10   Comparision of N-Δ curves between numerical and experimental results


总体来看，利用该模拟方法能够有效地模拟轴压加载过程，得到试件的极限荷载. 所有极限荷载的模拟值Fua和试验值Fue对比如表5所示，误差ξ1都小于10%.

表 5   极限荷载的模拟值与试验值对比

Tab.5  Ultimate load comparison between simulation and experimental results

编号 Fue /kN Fua /kN ξ1 /%
FS1-100-500 81.49 87.09 6.87
FS1-100-900 84.25 91.33 8.40
FS2-100-500 121.28 127.16 4.84
FS2-100-900 132.37 133.00 0.47
FS1-900-500 56.63 55.05 −2.79
FS1-900-900 60.27 62.51 3.72
FS2-900-500 78.34 75.82 −3.21
FS2-900-900 92.68 88.51 −4.50
FS1-1200-500 46.38 46.70 0.68
FS1-1200-900 50.80 52.79 3.92
FS2-1200-500 68.61 67.83 −1.13
FS2-1200-900 79.81 75.25 −5.70

新窗口打开| 下载CSV


基于上述有限元方法，对壁厚为1.0 mm和壁厚为2.0 mm的空钢管短柱试件进行有限元分析，可得空管短柱的承载力Fsteel. 将泡沫混凝土截面面积与其抗压强度的乘积定义为对应密度泡沫混凝土的轴压承载力Ffoam，如表6所示. 表中，Fsteel-1.0为1.0 mm厚钢管的承载力，Ffoam-500为密度为500 kg/m3的泡沫混凝土的承载力. 统计各部分材料对短柱构件极限承载力的贡献，如表7所示，剩余部分为泡沫混凝土与钢管间相互作用对极限承载力的贡献. 表中，Fsteel/F为钢管承载力贡献，Ffoam/F为泡沫混凝土承载力贡献，Fint/F为相互作用的贡献.

表 6   各部分材料的承载力

Tab.6  Bearing capacity of each part of material

kN
Fsteel-1.0 Fsteel-2.0 Ffoam-500 Ffoam-900
61.78 112.4 2.69 8.13

新窗口打开| 下载CSV


表 7   短柱试件各部分材料对极限承载力的贡献

Tab.7  Contribution of each part of the material to ultimate bearing capacity

%
编号 Fsteel/F Ffoam/F Fint/F
FS1-100-500 70.93 3.09 26.38
FS1-100-900 67.64 8.90 24.23
FS2-100-500 88.39 2.12 9.49
FS2-100-900 84.51 6.11 9.38

新窗口打开| 下载CSV


通过对各部分材料对极限承载力的贡献比值可以看出，随着壁厚和填充密度的增加，泡沫混凝土与钢管间的相互作用对极限承载力的贡献逐渐减小.

3.3. 参数分析

基于提出的有限元仿真方法，对泡沫混凝土填充圆钢管长柱构件轴压稳定承载力的主要影响因素进行参数分析，分析各影响因素对长柱构件的影响.

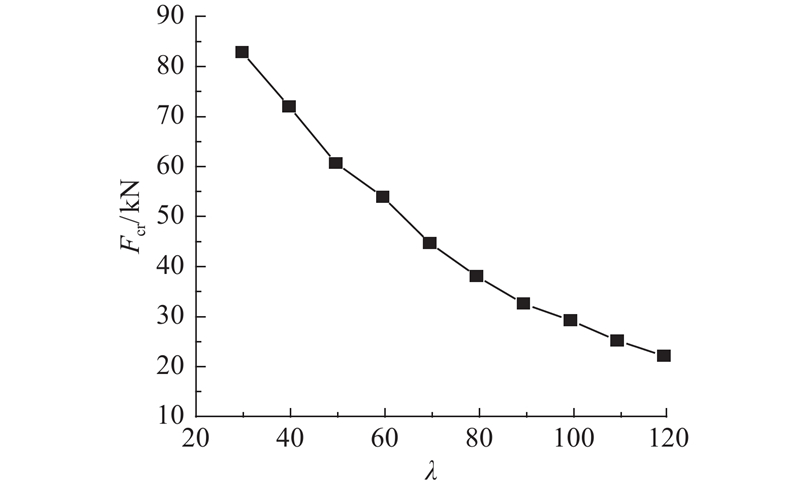
改变试件长度以获得不同长细比的构件，钢管壁厚为1 mm，填充密度为900 kg/m3，通过分析得到的稳定承载力Fcr如图11所示. 随着长细比的增大，稳定承载力呈反比例函数形式的下降趋势.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   稳定承载力与长细比关系曲线

Fig.11   Relationship of stable load and slenderness ratio


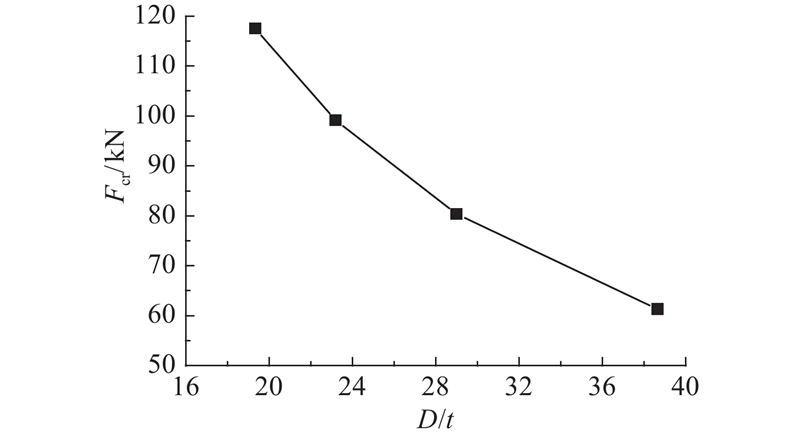
保持管径58 mm不变，调整圆钢管的壁厚以改变试件的径厚比，共选取38.7、29、23.2和19.3 4种径厚比，钢管长度为900 mm，填充泡沫混凝土密度为900 kg/m3，利用数值模拟得到的结果如图12所示. 长柱构件随着钢管径厚比的增大而逐渐减小，呈现出反比例函数关系.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   稳定承载力与径厚比的关系曲线

Fig.12   Relationship of stable load and diameter to thickness ratio


为了考察泡沫混凝土密度对试件稳定承载力的影响，特选取800、900、1 000、1 100、1 200 kg/m3 5种密度的泡沫混凝土，壁厚选取2 mm，试件长度为900 mm. 由于泡沫混凝土的力学性能与密度密切相关，数值模拟时需要知道每一种密度的泡沫混凝土的本构数据，参考熊耀清等[24]提出的硫铝酸盐泡沫混凝土本构模型，计算得到各密度泡沫混凝土的本构数据，如图13所示. 图中，σ为应力，ε为应变. 不同填充密度长柱试件的稳定承载力如图14所示，稳定承载力随着填充密度的增大而增大.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   泡沫混凝土的材料性能

Fig.13   Properties of foam concrete


图 14

新窗口打开| 下载原图ZIP| 生成PPT

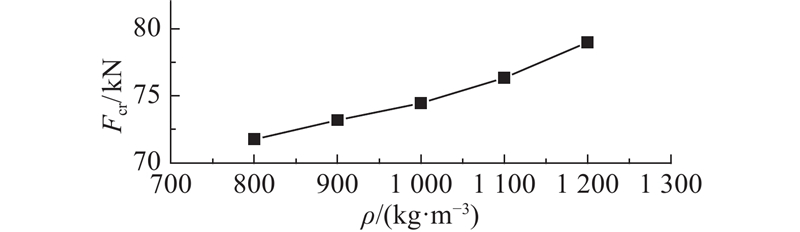
图 14   稳定承载力与泡沫混凝土填充密度的关系曲线

Fig.14   Relationship of stable load and concrete density


4. 长柱构件的极限承载力预测

由上述试验结果可知，长柱构件在轴压荷载作用下发生的是失稳破坏. 钢结构稳定设计理论[25]中，对轴心受压构件的稳定性计算通常采用2种处理方法，即Euler公式和Perry-Robertson公式. Euler公式的研究对象是理想线弹性压杆，典型的Euler临界力公式为

$ {N_{\rm cr}} = {{{{\text{π}} ^2}EA}}/{{{\lambda ^2}}}. $

后续大量学者在此基础上作出了更多的基础性研究并得到了一系列成果. Perry-Robertson公式是目前应用最广泛的考虑杆件存在缺陷时的稳定承载力公式，如下所示：

$ \left. {\begin{aligned} &{\varphi {\rm{ = }}\left[ {1 + (1 + \varepsilon_0 )/{{\bar \lambda }^2}} \right]/2 - \sqrt {{{\left[ {1 + (1 + \varepsilon_0 )/{{\bar \lambda }^2}} \right]}^2}/2 - 1/{{\bar \lambda }^2}} ,}\\ &{\varepsilon_0 = {v_0}A/W,}\\ &{\overline \lambda = \lambda \sqrt {{f_{\rm s}}/\left( {{{\text{π}} ^2}{E_{\rm s}'}} \right)} .} \end{aligned}} \right\} $

式中： $\varphi $为稳定性系数；v0为初弯曲，本文初弯曲取规范规定的初弯曲最大值l/1 000；ε0为相对初弯曲； ${\bar \lambda }$为相对长细比；A为截面面积；W为截面系数； $ E_{\rm s}'$为材料弹性模量；fs为材料的屈服强度.

泡沫混凝土填充圆钢管长柱构件在制备和运输的过程中由于碰撞一定会产生初始缺陷，以Perry-Robertson公式为基础，推导泡沫混凝土填充圆钢管长柱构件的轴压承载力公式.

抗弯刚度是稳定承载力的决定因素，因此基于抗弯刚度，可以计算出泡沫混凝土填充圆钢管长柱试件中泡沫混凝土的材料参与系数：

$ \psi = \frac{{{E_{\rm f}} {I_{\rm f}}}}{{{E_{\rm f}} {I_{\rm f}} + {E_{\rm s}} {I_{\rm s}}}}. $

式中：If、Is分别为泡沫混凝土和钢管的截面惯性矩. 其中泡沫混凝土的弹性模量参考何书明[26]的研究成果，结合本文的泡沫混泥土材料性能数据，可以表示为泡沫混凝土密度ρ的指数函数形式，如下所示：

$ {E_{\rm f}} = 169{\exp\;({0.001\rho }}). $

通过Ψ可以将泡沫混凝土等效为钢材，等效后的长柱截面面积Aeq和截面系数Weq分别如下：

$ {A_{\rm eq}} = {A_{\rm s}} + \psi {A_{\rm f}}{\text{，}} $

$ {W_{\rm eq}} = {W_{\rm s}} + \psi {W_{\rm f}}. $

将Aeq和Weq代回到式（3），可以得到泡沫混凝土填充圆钢管长柱试件的稳定系数. 得到稳定系数后，泡沫混凝图填充圆钢管长柱试件的稳定承载力可以表示为

$ {F_{\rm cr}} = \varphi {A_{\rm eq}}{f_{\rm s}}. $

利用推导的预测公式，对试验中的8根长柱试件进行稳定承载计算，得到的结果如表8所示. 表中，Fcre为稳定荷载试验值，Fcrp为稳定荷载预测值，ξ2为相对误差.

表 8   长柱构件稳定荷载预测值与试验值对比

Tab.8  Predicted stable load of long column members compared with experimental value

编号 Fcre /kN Fcrp /kN ξ2 /%
FS5810-900-500 56.63 57.13 0.88
FS5810-900-900 60.27 60.11 −0.27
FS5810-1200-500 46.38 45.55 −1.79
FS5810-1200-900 50.80 47.90 5.71
FS5820-900-500 78.34 82.34 5.11
FS5820-900-900 92.68 83.38 −10.03
FS5820-1200-500 68.61 71.78 4.62
FS5820-1200-900 79.81 72.16 −9.59

新窗口打开| 下载CSV


预测结果与试验结果能够很好地吻合，预测结果的相对误差约为5%，其中FS5820-900-900和FS582-1200-900的预测值和实验值相差较大，但与有限元模拟的结果相差较小，这说明试验中这2根试件的泡沫混凝土填充密度偏大，导致试件的稳定承载力偏高.

综上所述，基于Perry-Robertson公式提出的承载力预测公式（2）~（8），能够很好地预测泡沫混凝土填充圆钢管长柱构件的轴压稳定承载力.

5. 结　论

（1）泡沫混凝土填充圆钢管长柱构件的稳定承载力随着填充密度的提高而增大，随着长细比和径厚比的增大呈反比例函数关系减小.

（2）短柱构件叠缩过程中的轴向平均荷载随着填充泡沫混凝土密度的增大而增大，耗能能力显著增强. 随着壁厚和填充密度的增加，泡沫混凝土与钢管间的相互作用对极限承载力的贡献逐渐减小.

（3）基于Perry-Robertson公式，提出泡沫混凝土填充圆钢管长柱构件的稳定承载力计算公式，预测结果与试验结果吻合良好.

参考文献

于英华, 吴雪娜, 郎国军

泡沫铝汽车碰撞吸能器仿真分析

[J]. 世界科技研究与发展, 2012, 34 (2): 184- 187

[本文引用: 1]

YU Ying-hua, WU Xue-na, LANG Guo-jun

Simulation analysis of automobile collision energy-absorber

[J]. World Science-Technology Research and Development, 2012, 34 (2): 184- 187

[本文引用: 1]

KRETZ R, HAUSBERGER K, GÖTZINGER B

Energy-absorbing behavior of aluminum foams: head impact tests on the A-Pillar of a car

[J]. Advanced Engineering Materials, 2002, 4 (10): 781- 785

DOI:10.1002/1527-2648(20021014)4:10<781::AID-ADEM781>3.0.CO;2-U      [本文引用: 1]

BAROUTAJI A, GILCHRIST M D, SMYTH D, et al

Crush analysis and multi-objective optimization design for circular tube under quasi-static lateral loading

[J]. Thin-Walled Structures, 2015, 86: 121- 131

DOI:10.1016/j.tws.2014.08.018      [本文引用: 1]

YUEN S C K, NURICK G N, WITBEEN H L

The response of sandwich panels made of thin-walled tubes subjected to axial load

[J]. International Journal of Protective Structures, 2011, 2 (4): 477- 498

DOI:10.1260/2041-4196.2.4.477     

BØRVIK T, HOPPERSTAD O S, REYES A, et al

Empty and foam-filled circular aluminum tubes subjected to axial and oblique quasistatic loading

[J]. International Journal of Crashworthiness, 2003, 8 (5): 481- 494

DOI:10.1533/ijcr.2003.0254     

黄炼, 吕志强, 赵应龙

泡沫铝填充圆管轴向动力屈曲及吸能特性研究

[J]. 舰船科学技术, 2009, 31 (8): 55- 59

HUANG Lian, LV Zhi-qiang, ZHAO Ying-long

Studies on the asial dynamical buckling and energy absorption properties of aluminum foam-filled circular tubes

[J]. Ship Science and Technology, 2009, 31 (8): 55- 59

REZAEI B, NIKNEJAD A, ASSAEE H, et al

Axial splitting of empty and foam-filled circular composite tubes: an experimental study

[J]. Archives of Civil and Mechanical Engineering, 2015, 15 (3): 650- 662

DOI:10.1016/j.acme.2014.09.003     

REZVANI M J, JAFARIAN B

An experimental investigation on energy absorption of thin-walled bitubal structures by inversion and axial collapse

[J]. International Journal of Mechanical Sciences, 2017, 126: 270- 280

DOI:10.1016/j.ijmecsci.2017.03.005     

RAZAZAN M, REZVANI M J, SOUZANGARZADEH H

Evaluation of the performance of initiator on energy absorption of foam-filled rectangular tubes: experimental and numerical assessment

[J]. Experimental Techniques, 2017, 42 (9): 1- 11

[本文引用: 1]

REID S R, REDDY T Y, GRAY M D

Static and dynamic axial crushing of foam-filled sheet metal tubes

[J]. International Journal of Mechanical Sciences, 1986, 28 (5): 295- 322

DOI:10.1016/0020-7403(86)90043-3      [本文引用: 1]

桂良进, 范子杰, 王青春

泡沫填充圆管的轴向压缩能量吸收特性

[J]. 清华大学学报: 自然科学版, 2003, 43 (11): 1526- 1529

[本文引用: 1]

GUI Liang-jin, FAN Zi-jie, WANG Qing-chun

Energy-absorption properties of foam-filled circular tubes subjected to axial crushing

[J]. Journal of Tsinghua University: Science and Technology, 2003, 43 (11): 1526- 1529

[本文引用: 1]

程涛, 向宇, 李健, 等

泡沫铝填充多棱管的吸能分析

[J]. 振动与冲击, 2011, 30 (9): 237- 242

DOI:10.3969/j.issn.1000-3835.2011.09.049      [本文引用: 1]

CHENG Tao, XIANG Yu, LI Jian, et al

Energy absorption analysis of foamed aluminum-filled prisms

[J]. Journal of Vibration and Shock, 2011, 30 (9): 237- 242

DOI:10.3969/j.issn.1000-3835.2011.09.049      [本文引用: 1]

张景飞, 冯明德, 陈金刚

泡沫混凝土抗爆性能的试验研究

[J]. 混凝土, 2010, 10: 10- 12

DOI:10.3969/j.issn.1000-4637.2010.04.003      [本文引用: 1]

ZHANG Jing-fei, FENG Ming-de, CHEN Jin-gang

Study on the knock characteristic of foam concrete

[J]. Concrete, 2010, 10: 10- 12

DOI:10.3969/j.issn.1000-4637.2010.04.003      [本文引用: 1]

YUAN Pu, MA Qin-yong, ZHANG Hai-dong

Energy disspation analyses on light-weight foam concrete under impact loads

[J]. Electronic Journal of Geotechnical Engineering, 2014, 19: 8667- 8675

王代华, 刘殿书, 杜玉兰, 等

含泡沫吸能层防护结构爆炸能量分布的数值模拟研究

[J]. 爆炸与冲击, 2006, 26 (6): 562- 567

DOI:10.3321/j.issn:1001-1455.2006.06.015      [本文引用: 1]

WANG Dai-hua, LIU Dian-shu, DU Yu-lan, et al

Numerical simulation of anti-blasting mechanism and energy distribution of composite protective structure with foam concrete

[J]. Explosion and Shock Waves, 2006, 26 (6): 562- 567

DOI:10.3321/j.issn:1001-1455.2006.06.015      [本文引用: 1]

杨先锋, 张志强, 杨嘉陵, 等

飞机泡沫混凝土道面拦阻系统的阻滞性能研究

[J]. 兵工学报, 2017, 38 (增1): 155- 162

[本文引用: 1]

YANG Xian-feng, ZHANG Zhi-qiang, YANG Jia-ling, et al

Research on retardation performance of aircraft foamed concrete arreesting system

[J]. Acta Armamentarii, 2017, 38 (增1): 155- 162

[本文引用: 1]

BARDI F C, KYRIAKIDES S

Plastic buckling of circular tubes under axial compression—part I: experiments

[J]. International Journal of Mechanical Sciences, 2006, 48 (8): 830- 841

DOI:10.1016/j.ijmecsci.2006.03.005      [本文引用: 1]

BARDI F C, KYRIAKIDES S, YUN H D

Plastic buckling of circular tubes under axial compression—part II: analysis

[J]. International Journal of Mechanical Sciences, 2006, 48 (8): 842- 854

DOI:10.1016/j.ijmecsci.2006.03.002      [本文引用: 1]

李应权, 朱立德, 李菊丽, 等

泡沫混凝土配合比的设计

[J]. 徐州工程学院学报, 2011, 26 (2): 1- 5

DOI:10.3969/j.issn.1674-3571-B.2011.02.001      [本文引用: 1]

LI Ying-quan, ZHU Li-de, LI Ju-li, et al

Study on mix ratio design of foamed concrete

[J]. Journal of Xuzhou Institute of Technology, 2011, 26 (2): 1- 5

DOI:10.3969/j.issn.1674-3571-B.2011.02.001      [本文引用: 1]

金属材料室温拉伸试验方法: GB/T 228-2010 [S]. 北京: 中国标准出版社, 2010.

[本文引用: 1]

钢及钢产品力学性能试验取样位置及试样制备: GB/T 2975-1998 [S]. 北京: 中国标准出版社, 1998.

[本文引用: 1]

泡沫混凝土行业标准: JG/T 266-2011 [S]. 北京: 中国标准出版社, 2011.

[本文引用: 1]

GUILLOW S R, LU G, GRZEBIETA R H

Quasi-static axial compression of thin-walled circular aluminum tubes

[J]. International Journal of Mechanical Sciences, 2001, 43 (9): 2103- 2123

DOI:10.1016/S0020-7403(01)00031-5      [本文引用: 2]

熊耀清, 姚谦峰

轻质多孔混凝土受压应力-应变全曲线试验研究

[J]. 四川建筑科学研究, 2010, 36 (2): 228- 232

DOI:10.3969/j.issn.1008-1933.2010.02.059      [本文引用: 1]

XIONG Yao-qing, YAO Qian-feng

Experimental study on the total stress-strain curve of porous lightweight concrete

[J]. Sichuan Building Science, 2010, 36 (2): 228- 232

DOI:10.3969/j.issn.1008-1933.2010.02.059      [本文引用: 1]

陈骥. 钢结构稳定理论与设计[M]. 北京: 科学出版社, 2001.

[本文引用: 1]

何书明. 泡沫混凝土本构关系的研究 [D]. 吉林: 吉林建筑大学, 2014.

[本文引用: 1]

HE Shu-ming. Research about the constitutive relation of foam concrete [D]. Jilin: Jilin University of Architecture, 2014.

[本文引用: 1]

/

〈 〉