随着全球信息化水平的不断提高,计算机、网络和通信技术的不断发展以及技术创新热度的不断增加,信息化浪潮正深刻地影响着人们的生活[1]. 近年来,随着移动互联网、基于物联网的传感感知技术的不断发展,人们能够以多样化的方式了解和记录城市发展的脉络. 同时,基于位置的服务(location-based service,LBS)(如百度地图、谷歌地图等)可以帮助人们在日常生活中进行导航、定位,极大地便利了人们的生产生活,并且这些基于位置的服务设施在某种程度上记录了城市及周边地区的演化变迁过程,这为研究城市的发展变迁提供了可能.
城市兴趣点(point-of-interest,POI)是指电子地图上对人们有用的或者人们感兴趣的地理位置点,用以表示某一个地标、景点、商业点(商场、饭店、加油站等),主要是指与人们生活日益相关的地理实体,如学校、银行、饭店、超市等[2]. 在现代城市中,大量的兴趣点会呈现出从出现、成长、稳定一段时间后消亡的过程,这个过程称之为城市兴趣点的生命周期. 城市兴趣点的演化规律研究主要就是针对城市兴趣点的生命周期的研究. 如果可以获得一个城市的地理信息数据的微观演变历史,即城市特定区域的特定时刻的POI数据,就可以通过构建关于这座城市的在时间维度的地理快照,从而得到这个城市在其发展过程中的某一个时刻的详细的地理空间数据,进一步利用这些特定时刻的地理信息数据,分析该城市的POI的演化规律.
可预测性(Predictability)是指可以定性或定量地对系统状态进行正确预测的程度. 系统的可预测性范围的确定,有助于人们更加全面细致地理解系统,同时可用于评价针对系统的预测算法[3].
现阶段国内外针对POI所作的研究主要包括3个部分:1)POI的识别和推荐,2)基于POI数据的应用,3)POI生命周期的检测和识别.
POI的识别和推荐主要是采用基于位置的社交网络(location-based social networks,LBSN)和移动感知技术来得到大量用户有关于位置的日常活动信息,然后通过数据挖掘方法来识别现实世界的POI;在此基础上,通过对用户行为模式的挖掘并结合POI的类别信息等,实现基于用户偏好的POI推荐. 例如,Kennedy等[4]通过采集网络中具有代表性的图像使用无监督的方法来生成地标文本或者图像,实现对地理位置的标记. 针对POI的推荐方法研究可能是POI相关研究的最热门问题之一. 一些研究者通过对用户访问POI的轨迹进行分析,并结合其他地理或者时间因素,利用矩阵分解方法来提高POI推荐的准确性,减少相应计算的复杂度. 例如Lian等[5]通过使用加权矩阵分解方法提高针对POI的推荐性能; Cheng等[6]在此基础上提出了嵌入马尔科夫链和局部区域约束的新的矩阵分解方法,实现了基于LBSN的连续的个性化POI推荐服务.
此外,部分研究者着眼于开放的电子地图提供的丰富的POI数据,并基于这些数据研究针对于智慧城市的多种多样的应用. 其中有基于POI数据的城市功能区的识别,包括根据POI数据的空间分布和类别特征实现城市地区分层地标的提取[7]、针对POI数据使用核密度分析实现城市功能区以及POI热点分布的发现[8-9]. 一些工作者将城市地区的POI数据同其他移动感知数据和基于位置的社交网络数据结合,从而为用户提供更加丰富的服务. 其中包括将人群的流动模式同POI数据相结合,实现对人群运动语义学的刻画,进一步实现为出租车司机推荐载客地点,为乘客推荐候车地点[10]. Yu等[11]通过结合POI的时空结构来完成人类活动的早期识别,同时提出多级平衡随机森林结构来对人类活动进行预测.
总的来说,国内外针对POI的相关研究主要是POI的识别和检测、根据POI数据进行城市功能区的识别以及城市发展过程建模研究,实现了选址推荐、土地利用分析、房地产评估等城市服务. 通过对POI生命周期的检测和识别,进一步细粒度地刻画城市发展的脉络,把握城市发展变迁过程,对城市POI兴衰演变分析、以及城市的可持续发展建设来说具有重要意义,然而目前并没有针对城市POI演化规律的可预测性方面的相关分析研究.
本研究通过城市POI的生命周期数据来研究城市POI演化规律的可预测性,包括对7个城市的POI数据的生命周期长度和生命周期状态的分析和定义,对POI演化规律的刻画,实现POI演化过程中演化规律可预测性的量化.
1. 系统框架与POI数据的采集分析
1.1. 系统框架
通过对从OpenStreetMap上采集到的POI数据进行分析,提出POI生命周期可预测性分析(POI lifecycle predictability analysis,PLCPA)模型. 如图1所示,本模型由POI数据采集与整合、POI生命周期建模和POI生命周期可预测性分析3个部分组成. 针对POI演化规律的可预测性分析,首先将问题形式化为POI生命周期长度和POI生命周期状态的可预测性分析,然后结合信息熵理论,基于Fano不等式实现POI演化规律的可预测性分析.
图 1
图 1 兴趣点生命周期可预测性分析模型
Fig.1 Point-of-interest (POI) life cycle predictability analysis model
1.2. POI数据的采集分析
为了能够获得较为完整、准确的城市POI演化数据,从OpenStreetMap(OSM)中采集城市POI数据. OSM是一个开源的在线地图网站,允许用户提供、更新、维护世界各地的小路、餐厅、学校、基础设施等多种数据. OSM目前提供的基于位置的服务正处于快速发展的阶段,尚不完善,只能提供全球的地图演化数据,无法直接获取某一个地区或者某一个城市的地图演化数据. 为了获得目标区域的地图数据,首先从OSM网站上采集全球2011—2017这7年的地图数据,然后使用Osmosis结合目标区域的ploys文件提取目标区域的地图数据.
为了刻画城市POI生命周期的可预测性,要求目标区域的POI数据较为丰富,过于稀疏的POI数据不利于反映POI的演变过程. 通过对比分析发现,东京、柏林、纽约、伦敦、巴黎、北京和上海的POI数据相对丰富,使用Osmosis结合北京、柏林、伦敦、纽约、巴黎、东京、上海7个城市的polys文件,提取出对应的城市地图数据. 采集对应城市地图快照数据的基本过程如图2所示.
图 2
经过上面的一系列采集过程,得到区域集合 R={北京,柏林,伦敦,纽约,巴黎,上海,东京},对应每一个城市
表 1 每一个城市的主类别对应的POI数量
Tab.1
| 类别 | amenity | building | historic | leisure | shop | sport | tourism |
| 北京 | 3 992 | 24 | 0 | 130 | 1 609 | 0 | 747 |
| 柏林 | 23 308 | 19 | 0 | 2 002 | 18 617 | 64 | 1 210 |
| 伦敦 | 24 364 | 42 | 0 | 982 | 14 905 | 61 | 981 |
| 纽约 | 13 191 | 27 | 0 | 1 848 | 4 167 | 24 | 368 |
| 巴黎 | 18 065 | 28 | 0 | 422 | 12 741 | 23 | 1 291 |
| 上海 | 3 092 | 18 | 0 | 279 | 1 432 | 12 | 322 |
| 东京 | 37 485 | 20 | 1 | 1 024 | 22 665 | 14 | 832 |
通过Osmosis工具将这些空节点过滤掉,最终得到这7个城市具有丰富语义信息的POI地图快照数据,其中城市
对于快速发展的大城市
2. POI生命周期建模
对城市POI数据进行整合,得到POI的快照集合. 对于给定地区
定义1 POI生命周期长度. 对于任意一个POI,其生命周期所对应的时间区间
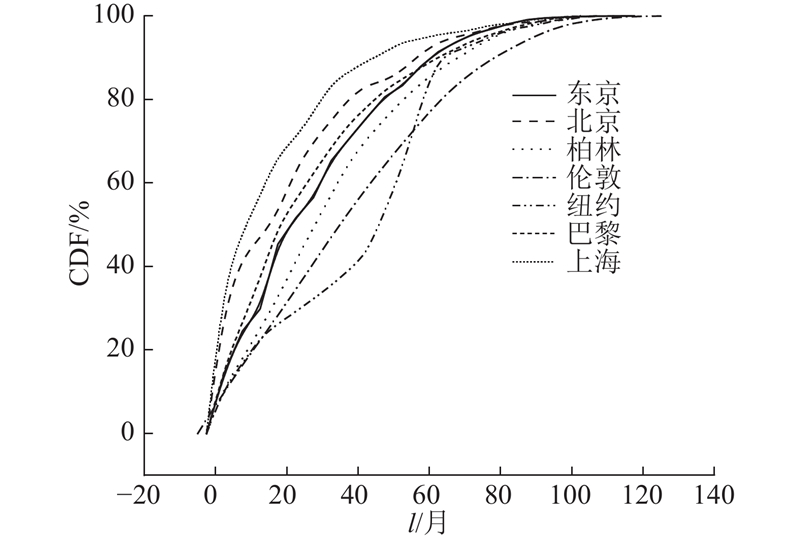
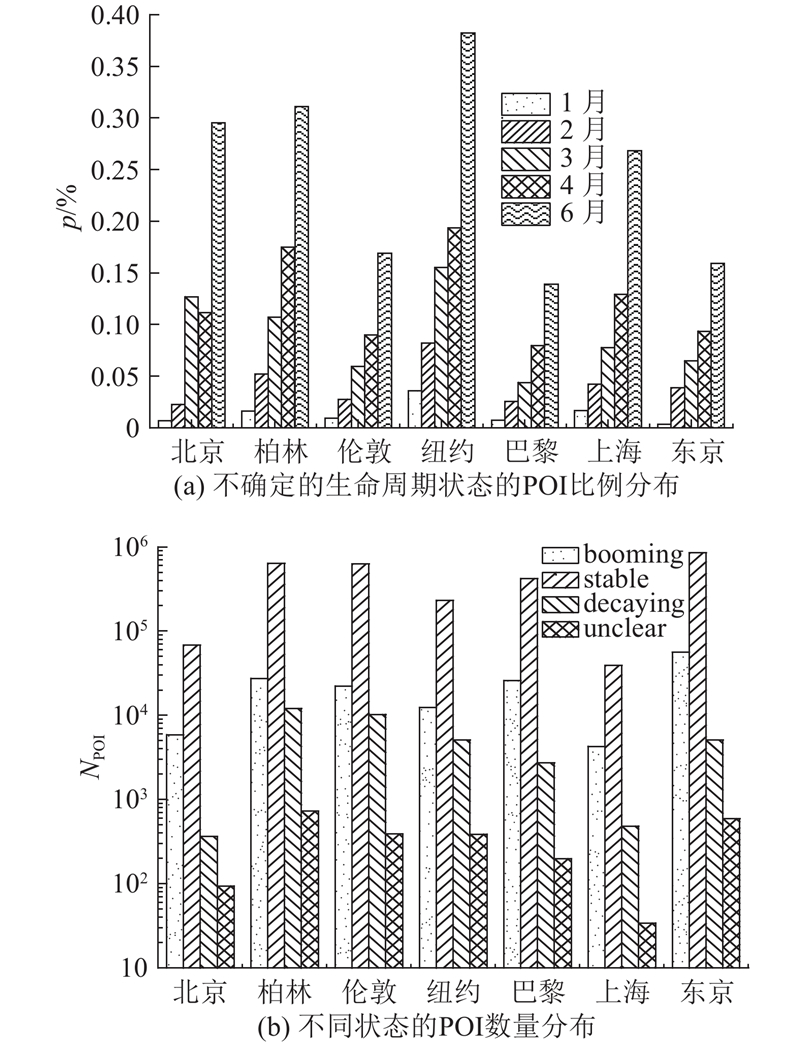
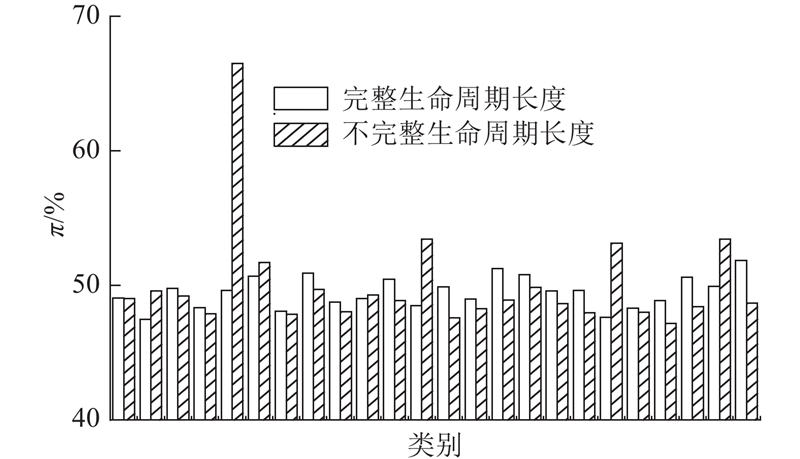
根据每一个POI是否具有明确的结束时间统计出每一个城市具有完整的生命周期的POI数量和不具有完整生命周期的POI数量的比例p,如图3所示. 从图中可以发现,每一个城市具有完整生命周期的POI数量远远低于不具有完整生命周期的POI数量. 计算每一个城市POI生命周期长度的累积分布(cumulative distribution function,CDF)情况,如图4所示为每一个城市POI生命周期长度的累积分布图. 对于所有的城市,超过90%的POI的生命周期长度少于80个月,也就是说基本上所有的POI的存活时间不超过6.7 a,说明这些城市的经济环境变化是动态的而且非常频繁. 因此关于POI推荐和商业选址等应用,在这些城市中是非常有价值的. 对于北京、上海来说,有超过90%的POI的生命周期长度少于45个月,这表明北京和上海的经济环境是非常活跃的,实际上自改革开放以来,北京地区第三产业取得长足发展且迅速成为北京的主导产业,对于经济发展的贡献率蹿升到了2016年的80.23%;而上海的经济发展水平也一直处于全国的前列[17]. 上海的POI的生命周期的长度整体要少于北京,这说明上海最近几年的经济环境相比于北京来说更加活跃,发展更加迅速.
图 4
图 3
图 5
图 5 纽约市不同类别POI生命长度的累积分布
Fig.5 Cumulative distribution of POI life lengths in different categories in New York City
POI在演变和发展过程中必然经历着从“出现”、“稳定发展”到最终“消亡”的生命状态的变化,并且在任意时刻,其生命周期状态只存在其中一种情况. 因此,在POI整个生命周期(包括上述的完整生命周期和不完整生命周期)中,必然存在1个时间窗口
定义2 POI生命周期状态. 对于由不同时间戳组成的时间窗口
对于特定时间窗口
应当注意的是,时间窗口
图 6
3. 可预测性分析建模
3.1. 熵与可预测性
其中,
3.2. 城市兴趣点生命周期可预测性定义
城市中的每一个POI个体都包含自身的位置关系、类别信息及其生命周期信息. 根据定义1和定义2,可以将POI演化规律分为2个方面进行描述,一种是POI的生命周期长度信息,另一种是POI生命周期状态信息,包括booming、stable、decaying三种状态. 对于POI的生命周期长度,设定其预测分析的问题如下:根据已知的某一类的POI在数据集中生命周期长度的分布(包括具有完整生命周期和不完整生命周期的POI),来预测该类POI的生命周期长度;将POI生命周期状态的可预测性分析问题定义如下:当已知前
3.2.1. POI生命周期长度的可预测性
对于具有完整生命周期的POI,根据POI生命周期长度的定义,可以获得具有完整生命周期的POI在其生命周期内所跨越的时间长度
3.2.2. POI生命周期状态的可预测性
根据定义2,无论是对于具有完整生命周期的POI还是不具有完整生命周期的POI,都将其生命周期状态划分为booming、stable、decaying中的一个,而生命周期状态可以根据式(1)来确定. 同样根据POI类别将POI进行组合,得到每一个时间窗口每一类兴趣点的生命周期状态的集合{booming, stable, decaying},而对于每一个时间窗口,不同状态的POI所占比重不同,对于时间窗口
确定了连续时间窗口内POI状态变化情况后,就可以将POI生命周期状态的可预测性分析形式化描述为:当已知某一个城市的POI在前
4. 城市POI生命周期可预测性分析
4.1. 城市POI生命周期长度的可预测性分析
城市POI的生命周期长度是随时间而不断演化发展的,熵是表征时间序列可预测性的最基本的量[19],使用POI生命周期的熵来表征随时间序列变化的量的可预测性. 定义2种信息熵,一种是随机熵:
另一个是信息熵E(见式(2)).当随机熵和信息熵相等时,可以认为POI生命周期长度的分布是完全随机的,也就是说能够正确预测其生命周期长度的概率为
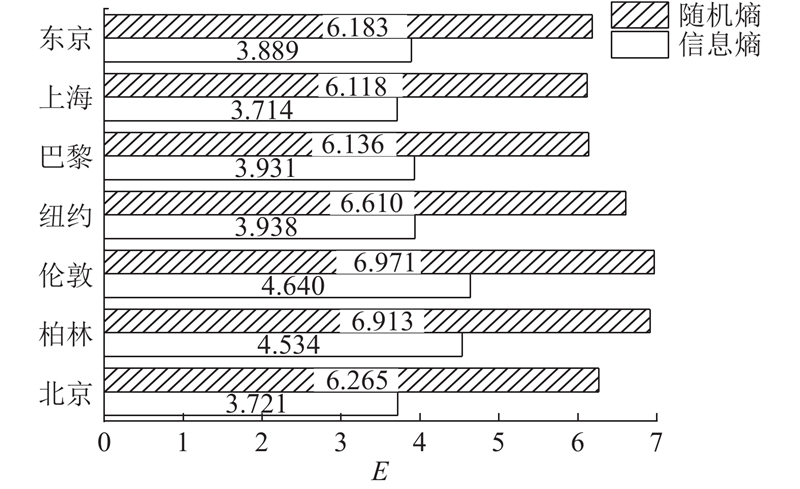
如图7所示为每一个城市中POI生命周期长度的熵值分布. 从图中可知,每一个城市POI生命周期长度的随机熵总是大于对应的信息熵,说明POI生命周期长度的分布并不是完全随机的,对于其生命周期的可预测性分析是有意义的.
图 7
可预测性的一个重要指标是适当的算法能够正确预测某一类新出现的POI的生命周期的长度的概率,而这个概率受到Fano不等式的限制,也就是说对于给定的POI生命周期长度的熵和其历史POI生命周期长度的分布,可以计算出这一类的POI的生命周期长度的可预测性. 根据式(3)可以求出每一类POI生命周期长度的可预测性,即对于某一类POI,如果其
图 8
图 9
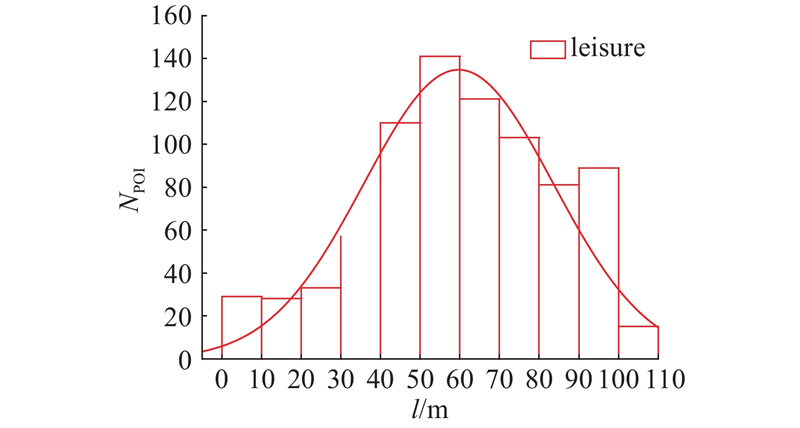
图 9 leisure类别POI的生命周期长度频次分布
Fig.9 Frequency distribution of life cycle length of POI in leisure category
进一步分析每一个子类对应的POI生命周期的可预测性,如图10所示为巴黎地区所有的POI子类所对应的生命周期长度的可预测性,其中可预测性最高的类别为 “motel”类,可预测性为100%,原始数据中巴黎地区具有完整生命周期的属于“motel”类别的POI只有2个,并且其生命周期长度都为5个月. 进一步分析数据,发现每一个城市的每一个子类的POI数量分布极其不均匀,图11(a)是伦敦地区不同子类对应的POI的个数的分布. 其中不同子类对应的POI数量差距明显,而且在每一个城市中都存在语义相同的子类,例如纽约地区的“fitness”、“fitness center”、“fitness station”的语义都是相同的,却被分为不同的类别,这是不合理的,将对生命周期长度的可预测性分析造成干扰. 为了平衡不同类别的POI数量以及中和那些语义相同而划分为不同类别的POI,将子类按照语义相似性进行整合得到初级类. 如图11(b)是伦敦市初级类对应的POI的数量分布.
图 10
图 11
在对POI类别进行整合之后,根据定义的POI生命周期长度的可预测性分析方法,得到初级类对应的POI生命周期长度的可预测性. 如图12所示为伦敦地区初级类对应的POI生命周期长度的可预测性分布. 从图中可以发现基本上所有类别的具有完整生命周期的POI生命周期长度的可预测性都高于不具有完整生命周期的POI的初级类别. 通过分析每一个城市的初级类别的POI生命周期的可预测性,发现每一个城市的POI生命周期长度的可预测性也是不相同的. 对于北京地区来说,所有初级类别的POI的生命周期长度的可预测大于50%,高于伦敦地区的POI生命周期长度的可预测性.
图 12
图 12 初级类别POI生命周期长度的可预测性
Fig.12 Predictability of POIs life cycle length in primary categories
4.2. 城市POI生命周期状态的可预测性分析
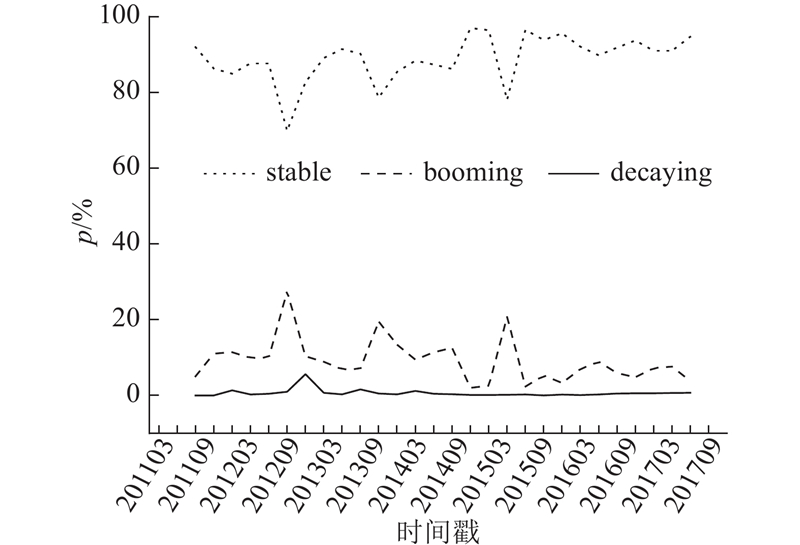
根据定义2,每一个POI完整的生命周期都包括boomin、stable和decaying 3种状态。时间窗口的大小为3个月,每一个时间窗口对应的POI的生命周期状态都可由式(1)确定. POI生命周期的状态是随着时间不断演化的,在每一个时间窗口中都存在不同数量的booming, stable, decaying这3种状态的POI,各占有一定的比重,对于所有的时间窗口,可以得到3种状态在所有时间窗口所占比重的集合. 如图13所示为北京市不同状态POI在所有时间窗口所占比重的分布,其中横坐标为时间戳,可以计算出不同状态POI所占比重的集合:
图 13
图 13 北京市不同生命周期状态的POI所占的比例
Fig.13 Proportion of POIs in different life cycle states in Beijing
对于每一种生命状态,都可以求解其在全部时间窗口POI所占比重的熵,刻画在历史过程中该状态的POI所占比重的分布的规律性.
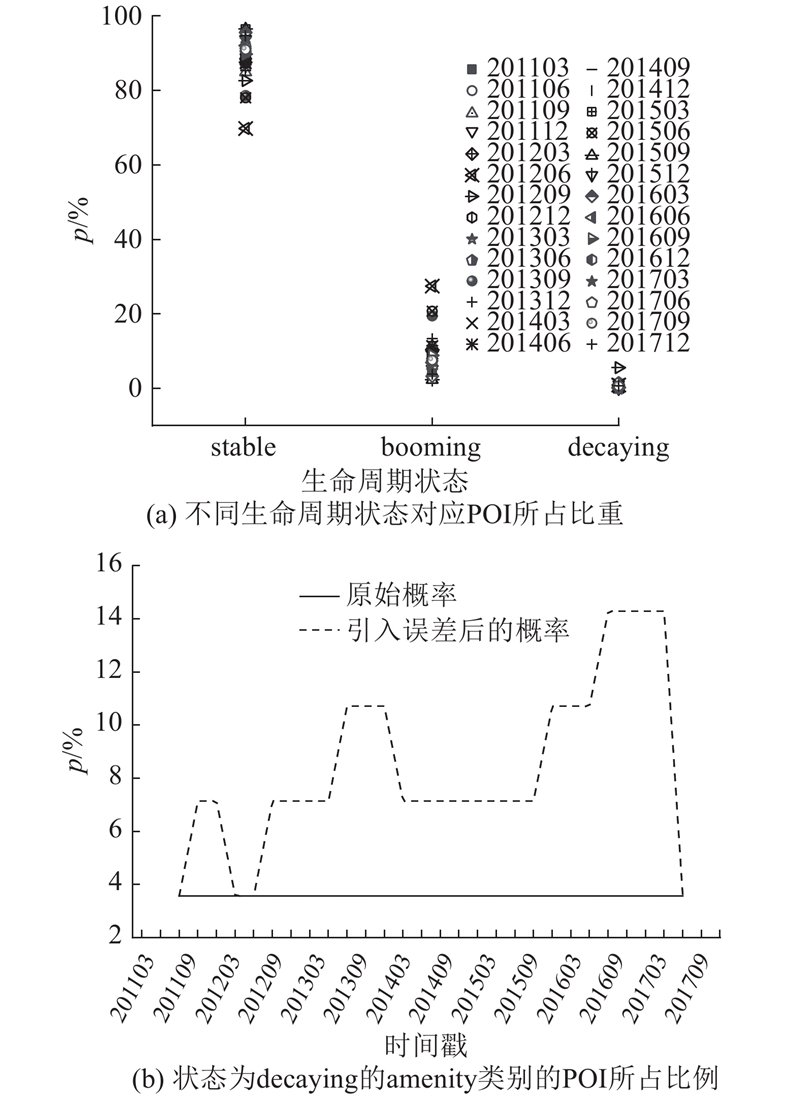
求解POI在前
通过对不同状态POI所占比重集合
图 14
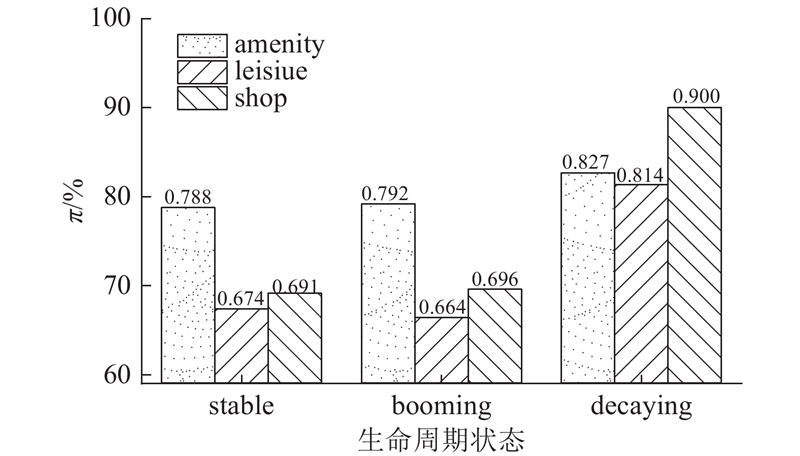
对于连续时间窗口的POI生命周期状态所占比重的分布,根据式(2)可以得到POI状态的信息熵,同时N为某一状态在连续时间窗口中不同比重的个数,根据式(3)可以得到POI某一生命周期状态的可预测性。如图15所示为伦敦地区不同类别POI 3中状态下的可预测性。不同类别的POI对应的生命周期状态的可预测性不同,amenity类别的POI对应的stable和booming的生命周期状态的可预测性要高于另外的两个类别。同一类别不同状态的POI的可预测性不同,对于shop类别的POI,stable状态的可预测性远低于decaying状态的可预测性。
图 15
图 15 伦敦市不同类别、不同状态POI的可预测性
Fig.15 Predictability of POIs in different categories and different states in London
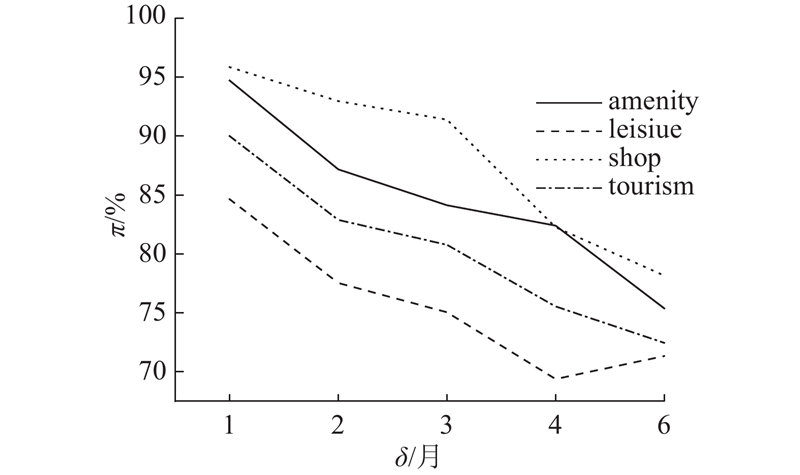
如图16所示为东京地区4个主类别对应的时间窗口分别为1、2、3、4和6个月时生命周期状态为decaying的POI所占比重的可预测性大小. 可知,时间窗口越大,其对应的生命周期状态的可预测性越小,并且shop类别对应decaying状态的POI所占比重的可预测性最大,而leisure类别的可预测性最小.
图 16
图 16 不同时间窗口对应的POI生命状态的可预测性
Fig.16 Predictability of POI life state corresponding to different time windows
5. 结 语
本研究通过定义POI生命周期长度和生命周期状态,形式化表示POI的时间序列信息,并结合信息论的方法将POI时间序列数据同信息熵和Fano不等式结合,构建POI演化规律的可预测性分析模型. 计算出7个城市的POI生命周期长度和状态的可预测性,其中处于消亡状态的POI的可预测性超过80%,而占比较大的稳定状态的POI的可预测性小于处于消亡状态的POI,从理论上说明处于消亡状态的POI在时间上的分布更加稳定.
然而OSM上的POI数据过于稀疏,只占真实POI数据的4%左右. 在以后的工作中将结合其他在线地图的POI数据进一步分析POI演化规律的可预测性. 在POI生命周期状态划分过程中,在结合POI生命周期长度信息的同时,可以对城市不同区域进行划分,更加有针对性地对在不同区域且具有不同演化过程的POI的演化规律的可预测性进行分析,从而实现更细粒度的POI生命周期状态的可预测性分析. POI演化规律的可预测性表示了能够准确预测POI生命周期的上界,采用何种预测算法能够逼近甚至达到该上界是一个重要的研究问题.
参考文献
Survey of data-centric smart city
[J].
复杂网络链路预测
[J].
Link Prediction on complex networks
[J].
Extracting hierarchical landmarks from urban POI data
[J].
基于 POI 数据的城市边界变化提取研究——以山西运城市城区为例
[J].
Study on urban boundary identification based on POI: a case study of Yuncheng City in Shanxi
[J].
设施 POI 分布热点分析的网络核密度估计方法
[J].
Network kernel density estimation for the analysis of facility POI hotspots
[J].
Predictability, complexity, and learning
[J].
Stock return predictability:Is it there?
[J].
Limits of predictability in human mobility
[J].
Patterns, entropy, and predictability of human mobility and life
[J].
Entropy and the predictability of online life
[J].
Predictability and information theory. Part I: measures of predictability
[J].