[1]
WANG X, ZENG X, LI J, et al A review on recent advancements of substructures for offshore wind turbines
[J]. Energy Conversion and Management , 2018 , 158 : 103 - 119
DOI:10.1016/j.enconman.2017.12.061
[本文引用: 1]
[2]
PASSON P Damage equivalent wind-wave correlations on basis of damage contour lines for the fatigue design of offshore wind turbines
[J]. Renewable Energy , 2015 , 81 : 723 - 736
DOI:10.1016/j.renene.2015.03.070
[本文引用: 1]
[3]
ZIEGLER L, VOORMEEREN S, SCHAFHIRT S, et al Design clustering of offshore wind turbines using probabilistic fatigue load estimation
[J]. Renewable Energy , 2016 , 91 : 425 - 433
DOI:10.1016/j.renene.2016.01.033
[4]
DO T Q, LINDT J W V D, MAHMOUD H Fatigue life fragilities and performance-based design of wind turbine tower base connections
[J]. Journal of Structural Engineering , 2015 , 141 (7 ): 04014183
DOI:10.1061/(ASCE)ST.1943-541X.0001150
[本文引用: 1]
[5]
JIA J An efficient nonlinear dynamic approach for calculating wave induced fatigue damage of offshore structures and its industrial applications for lifetime extension
[J]. Applied Ocean Research , 2008 , 30 (3 ): 189 - 198
DOI:10.1016/j.apor.2008.09.003
[本文引用: 1]
[6]
KVITTEM M I, MOAN T Time domain analysis procedures for fatigue assessment of a semi-submersible wind turbine
[J]. Marine Structures , 2015 , 40 : 38 - 59
DOI:10.1016/j.marstruc.2014.10.009
[本文引用: 1]
[7]
DU J, LI H, ZHANG M, et al A novel hybrid frequency-time domain method for the fatigue damage assessment of offshore structures
[J]. Ocean Engineering , 2015 , 98 : 57 - 65
DOI:10.1016/j.oceaneng.2015.02.004
[本文引用: 1]
[8]
MOHAMMADI S F, GALGOUL N S, STAROSSEK U, et al An efficient time domain fatigue analysis and its comparison to spectral fatigue assessment for an offshore jacket structure
[J]. Marine Structures , 2016 , 49 : 97 - 115
DOI:10.1016/j.marstruc.2016.05.003
[本文引用: 1]
[9]
TUNNA J M Fatigue life prediction for gaussian random loads at the design stage
[J]. Fatigue and Fracture of Engineering Materials and Structures , 2010 , 9 (3 ): 169 - 184
[本文引用: 1]
[10]
BENASCIUTTI D, TOVO R Spectral methods for lifetime prediction under wide-band stationary random processes
[J]. International Journal of Fatigue , 2005 , 27 (8 ): 867 - 877
DOI:10.1016/j.ijfatigue.2004.10.007
[11]
DIRLIK T. Application of computers in fatigue analysis [D]. Warwich: Warwich University, 1985: 129.
[12]
PARK J B, CHOUNG J, KIM K S A new fatigue prediction model for marine structures subject to wide band stress process
[J]. Ocean Engineering , 2014 , 76 (1 ): 144 - 151
[本文引用: 1]
[13]
BENASCIUTTI D, TOVO R Comparison of spectral methods for fatigue analysis of broad-band Gaussian random processes
[J]. Probabilistic Engineering Mechanics , 2006 , 21 (4 ): 287 - 299
DOI:10.1016/j.probengmech.2005.10.003
[本文引用: 1]
[15]
JIAO G, MOAN T Probabilistic analysis of fatigue due to Gaussian load processes
[J]. Probabilistic Engineering Mechanics , 1990 , 5 (2 ): 76 - 83
DOI:10.1016/0266-8920(90)90010-H
[16]
FU T T, CEBON D Predicting fatigue lives for bi-modal stress spectral densities
[J]. International Journal of Fatigue , 2000 , 22 (1 ): 11 - 21
DOI:10.1016/S0142-1123(99)00113-9
[17]
GAO S, ZHENG X Y An improved spectral discretization method for fatigue damage assessment of bimodal Gaussian processes
[J]. International Journal of Fatigue , 2019 , 119 : 268 - 280
DOI:10.1016/j.ijfatigue.2018.09.027
[本文引用: 1]
[18]
DNV GL. Fatigue design of offshore steel structures: DNVGL-RP-C203[S]. Norway: DNV GL, 2016: 178.
[本文引用: 1]
[19]
HUANG W, MOAN T. Fatigue under combined high and low frequency loads [C]// 25th International Conference on Offshore Mechanics and Arctic Engineering . Hamburg: OMAE, 2006: 149-156.
[20]
MA Y L, HAN C H, QU X Q Fatigue assessment method of marine structures subjected to two Gaussian random loads
[J]. Ocean Engineering , 2018 , 165 : 107 - 122
DOI:10.1016/j.oceaneng.2018.07.033
[本文引用: 1]
[21]
YAMASHITA A, SEKITA K. Analysis of the fatigue damage on the offshore wind turbines exposed to wind and wave loads within the typhoon area [C] // ASME 2004, International Conference on Offshore Mechanics and Arctic Engineering . Vancouver: ASME, 2004: 284-291.
[本文引用: 1]
[22]
DONG W, MOAN T, GAO Z Long-term fatigue analysis of multi-planar tubular joints for jacket-type offshore wind turbine in time domain
[J]. Engineering Structures , 2011 , 33 (6 ): 2002 - 2014
DOI:10.1016/j.engstruct.2011.02.037
[本文引用: 1]
[23]
YETER B, GARBATOV Y, SOARES C G Fatigue damage assessment of fixed offshore wind turbine tripod support structures
[J]. Engineering Structures , 2015 , 101 : 518 - 528
DOI:10.1016/j.engstruct.2015.07.038
[本文引用: 1]
[24]
TEMPEL J. Design of support structures for offshore wind turbines [D]. Delft: Delft University of Technology, 2006: 162.
[本文引用: 1]
[25]
ZIEGLER L, VOORMEEREN S, SCHAFHIRT S, et al Sensitivity of wave fatigue loads on offshore wind turbines under varying site conditions
[J]. Energy Procedia , 2015 , 80 : 193 - 200
DOI:10.1016/j.egypro.2015.11.422
[本文引用: 1]
[26]
MARINO E, GIUSTI A, MANUEL L Offshore wind turbine fatigue loads: the influence of alternative wave modeling for different turbulent and mean winds
[J]. Renewable Energy , 2017 , 102 : 157 - 169
DOI:10.1016/j.renene.2016.10.023
[本文引用: 1]
[27]
REZAEI R, FROMME P, DUFFOUR P Fatigue life sensitivity of monopile-supported offshore wind turbines to damping
[J]. Renewable Energy , 2018 , 123 : 450 - 459
DOI:10.1016/j.renene.2018.02.086
[本文引用: 1]
[28]
VALAMANESH V, MYERS A T Aerodynamic damping and seismic response of horizontal axis wind turbine towers
[J]. Journal of Structural Engineering , 2014 , 140 (11 ): 04014090
DOI:10.1061/(ASCE)ST.1943-541X.0001018
[本文引用: 1]
[29]
DAMGAARD M, ANDERSEN J K F, IBSEN L B, et al. Natural frequency and damping estimation of an offshore wind turbine structure [C] // Twenty-second International Offshore and Polar Engineering Conference . Rhodes: ISOPE, 2012: 300-307.
[本文引用: 1]
[30]
CARSWELL W, JOHANSSON J, LØVHOLT F, et al Foundation damping and the dynamics of offshore wind turbine monopiles
[J]. Renewable Energy , 2015 , 80 : 724 - 736
DOI:10.1016/j.renene.2015.02.058
[本文引用: 3]
[31]
DAMGAARD M, IBSEN L B, ANDERSEN L V, et al Cross-wind modal properties of offshore wind turbines identified by full scale testing
[J]. Journal of Wind Engineering and Industrial Aerodynamics , 2013 , 116 (5 ): 94 - 108
[本文引用: 2]
[32]
IEC.Wind turbines-Part 1: Design requirements: IEC 61400-1 [S]. Switzerland: International Electrotechnical Commission, 2005:66.
[本文引用: 1]
[33]
HANSEN M O L. 风力机空气动力学[M]. 北京: 中国电力出版社, 2009: 39-46.
[本文引用: 1]
[34]
俞聿修. 随机波浪及其工程应用[M]. 大连: 大连理工大学出版社, 2003: 221-223, 348-351.
[本文引用: 1]
A review on recent advancements of substructures for offshore wind turbines
1
2018
... 目前已运行的海上风电场中,风机基础型式采用单桩基础的比例近80%[1 ] ,是应用最广泛的基础型式. 海上风机的运行环境恶劣,风机基础结构长期受到循环载荷作用,易发生疲劳破坏[2 -4 ] . ...
Damage equivalent wind-wave correlations on basis of damage contour lines for the fatigue design of offshore wind turbines
1
2015
... 目前已运行的海上风电场中,风机基础型式采用单桩基础的比例近80%[1 ] ,是应用最广泛的基础型式. 海上风机的运行环境恶劣,风机基础结构长期受到循环载荷作用,易发生疲劳破坏[2 -4 ] . ...
Design clustering of offshore wind turbines using probabilistic fatigue load estimation
0
2016
Fatigue life fragilities and performance-based design of wind turbine tower base connections
1
2015
... 目前已运行的海上风电场中,风机基础型式采用单桩基础的比例近80%[1 ] ,是应用最广泛的基础型式. 海上风机的运行环境恶劣,风机基础结构长期受到循环载荷作用,易发生疲劳破坏[2 -4 ] . ...
An efficient nonlinear dynamic approach for calculating wave induced fatigue damage of offshore structures and its industrial applications for lifetime extension
1
2008
... 为了准确评价海洋结构物的疲劳损伤,需要进行全时域的动力分析. Jia[5 ] 对波浪载荷作用下的导管架结构进行了时域疲劳损伤分析,为缩减计算时间对工况进行了合并简化. Kvittem等[6 ] 在进行时域疲劳分析时,发现当模拟时长大于1 h时,模拟时段内随机性对损伤计算的影响降低. ...
Time domain analysis procedures for fatigue assessment of a semi-submersible wind turbine
1
2015
... 为了准确评价海洋结构物的疲劳损伤,需要进行全时域的动力分析. Jia[5 ] 对波浪载荷作用下的导管架结构进行了时域疲劳损伤分析,为缩减计算时间对工况进行了合并简化. Kvittem等[6 ] 在进行时域疲劳分析时,发现当模拟时长大于1 h时,模拟时段内随机性对损伤计算的影响降低. ...
A novel hybrid frequency-time domain method for the fatigue damage assessment of offshore structures
1
2015
... 全时域计算非常耗时,频域疲劳分析则相对简便. ABS规范给出了窄带响应下的疲劳损伤频域计算方法,Du等[7 ] 利用该方法计算了波浪载荷作用下的单桩基础海洋平台的疲劳损伤,并将其与时域分析结果对比,发现频域法计算的疲劳损伤是时域法结果的3.4倍. Mohammadi等[8 ] 认为ABS规范频域法计算结果过于保守的原因在于实际的应力幅概率分布并不严格符合ABS规范所假定的Rayleigh分布. 为此,一些学者提出适用于宽带过程的疲劳损伤分析方法[9 -12 ] . Benasciutti等[13 ] 研究了频域法的宽带过程疲劳问题,并讨论了带宽参数的取值与组合对疲劳损伤的影响. 双峰过程是宽带过程的1种特例[14 ] ,可由组合谱法[14 -17 ] 和疲劳损伤组合法[18 -20 ] 计算. ...
An efficient time domain fatigue analysis and its comparison to spectral fatigue assessment for an offshore jacket structure
1
2016
... 全时域计算非常耗时,频域疲劳分析则相对简便. ABS规范给出了窄带响应下的疲劳损伤频域计算方法,Du等[7 ] 利用该方法计算了波浪载荷作用下的单桩基础海洋平台的疲劳损伤,并将其与时域分析结果对比,发现频域法计算的疲劳损伤是时域法结果的3.4倍. Mohammadi等[8 ] 认为ABS规范频域法计算结果过于保守的原因在于实际的应力幅概率分布并不严格符合ABS规范所假定的Rayleigh分布. 为此,一些学者提出适用于宽带过程的疲劳损伤分析方法[9 -12 ] . Benasciutti等[13 ] 研究了频域法的宽带过程疲劳问题,并讨论了带宽参数的取值与组合对疲劳损伤的影响. 双峰过程是宽带过程的1种特例[14 ] ,可由组合谱法[14 -17 ] 和疲劳损伤组合法[18 -20 ] 计算. ...
Fatigue life prediction for gaussian random loads at the design stage
1
2010
... 全时域计算非常耗时,频域疲劳分析则相对简便. ABS规范给出了窄带响应下的疲劳损伤频域计算方法,Du等[7 ] 利用该方法计算了波浪载荷作用下的单桩基础海洋平台的疲劳损伤,并将其与时域分析结果对比,发现频域法计算的疲劳损伤是时域法结果的3.4倍. Mohammadi等[8 ] 认为ABS规范频域法计算结果过于保守的原因在于实际的应力幅概率分布并不严格符合ABS规范所假定的Rayleigh分布. 为此,一些学者提出适用于宽带过程的疲劳损伤分析方法[9 -12 ] . Benasciutti等[13 ] 研究了频域法的宽带过程疲劳问题,并讨论了带宽参数的取值与组合对疲劳损伤的影响. 双峰过程是宽带过程的1种特例[14 ] ,可由组合谱法[14 -17 ] 和疲劳损伤组合法[18 -20 ] 计算. ...
Spectral methods for lifetime prediction under wide-band stationary random processes
0
2005
A new fatigue prediction model for marine structures subject to wide band stress process
1
2014
... 全时域计算非常耗时,频域疲劳分析则相对简便. ABS规范给出了窄带响应下的疲劳损伤频域计算方法,Du等[7 ] 利用该方法计算了波浪载荷作用下的单桩基础海洋平台的疲劳损伤,并将其与时域分析结果对比,发现频域法计算的疲劳损伤是时域法结果的3.4倍. Mohammadi等[8 ] 认为ABS规范频域法计算结果过于保守的原因在于实际的应力幅概率分布并不严格符合ABS规范所假定的Rayleigh分布. 为此,一些学者提出适用于宽带过程的疲劳损伤分析方法[9 -12 ] . Benasciutti等[13 ] 研究了频域法的宽带过程疲劳问题,并讨论了带宽参数的取值与组合对疲劳损伤的影响. 双峰过程是宽带过程的1种特例[14 ] ,可由组合谱法[14 -17 ] 和疲劳损伤组合法[18 -20 ] 计算. ...
Comparison of spectral methods for fatigue analysis of broad-band Gaussian random processes
1
2006
... 全时域计算非常耗时,频域疲劳分析则相对简便. ABS规范给出了窄带响应下的疲劳损伤频域计算方法,Du等[7 ] 利用该方法计算了波浪载荷作用下的单桩基础海洋平台的疲劳损伤,并将其与时域分析结果对比,发现频域法计算的疲劳损伤是时域法结果的3.4倍. Mohammadi等[8 ] 认为ABS规范频域法计算结果过于保守的原因在于实际的应力幅概率分布并不严格符合ABS规范所假定的Rayleigh分布. 为此,一些学者提出适用于宽带过程的疲劳损伤分析方法[9 -12 ] . Benasciutti等[13 ] 研究了频域法的宽带过程疲劳问题,并讨论了带宽参数的取值与组合对疲劳损伤的影响. 双峰过程是宽带过程的1种特例[14 ] ,可由组合谱法[14 -17 ] 和疲劳损伤组合法[18 -20 ] 计算. ...
A method for accurate estimation of the fatigue damage induced by bimodal processes
2
2010
... 全时域计算非常耗时,频域疲劳分析则相对简便. ABS规范给出了窄带响应下的疲劳损伤频域计算方法,Du等[7 ] 利用该方法计算了波浪载荷作用下的单桩基础海洋平台的疲劳损伤,并将其与时域分析结果对比,发现频域法计算的疲劳损伤是时域法结果的3.4倍. Mohammadi等[8 ] 认为ABS规范频域法计算结果过于保守的原因在于实际的应力幅概率分布并不严格符合ABS规范所假定的Rayleigh分布. 为此,一些学者提出适用于宽带过程的疲劳损伤分析方法[9 -12 ] . Benasciutti等[13 ] 研究了频域法的宽带过程疲劳问题,并讨论了带宽参数的取值与组合对疲劳损伤的影响. 双峰过程是宽带过程的1种特例[14 ] ,可由组合谱法[14 -17 ] 和疲劳损伤组合法[18 -20 ] 计算. ...
... [14 -17 ]和疲劳损伤组合法[18 -20 ] 计算. ...
Probabilistic analysis of fatigue due to Gaussian load processes
0
1990
Predicting fatigue lives for bi-modal stress spectral densities
0
2000
An improved spectral discretization method for fatigue damage assessment of bimodal Gaussian processes
1
2019
... 全时域计算非常耗时,频域疲劳分析则相对简便. ABS规范给出了窄带响应下的疲劳损伤频域计算方法,Du等[7 ] 利用该方法计算了波浪载荷作用下的单桩基础海洋平台的疲劳损伤,并将其与时域分析结果对比,发现频域法计算的疲劳损伤是时域法结果的3.4倍. Mohammadi等[8 ] 认为ABS规范频域法计算结果过于保守的原因在于实际的应力幅概率分布并不严格符合ABS规范所假定的Rayleigh分布. 为此,一些学者提出适用于宽带过程的疲劳损伤分析方法[9 -12 ] . Benasciutti等[13 ] 研究了频域法的宽带过程疲劳问题,并讨论了带宽参数的取值与组合对疲劳损伤的影响. 双峰过程是宽带过程的1种特例[14 ] ,可由组合谱法[14 -17 ] 和疲劳损伤组合法[18 -20 ] 计算. ...
1
... 全时域计算非常耗时,频域疲劳分析则相对简便. ABS规范给出了窄带响应下的疲劳损伤频域计算方法,Du等[7 ] 利用该方法计算了波浪载荷作用下的单桩基础海洋平台的疲劳损伤,并将其与时域分析结果对比,发现频域法计算的疲劳损伤是时域法结果的3.4倍. Mohammadi等[8 ] 认为ABS规范频域法计算结果过于保守的原因在于实际的应力幅概率分布并不严格符合ABS规范所假定的Rayleigh分布. 为此,一些学者提出适用于宽带过程的疲劳损伤分析方法[9 -12 ] . Benasciutti等[13 ] 研究了频域法的宽带过程疲劳问题,并讨论了带宽参数的取值与组合对疲劳损伤的影响. 双峰过程是宽带过程的1种特例[14 ] ,可由组合谱法[14 -17 ] 和疲劳损伤组合法[18 -20 ] 计算. ...
Fatigue assessment method of marine structures subjected to two Gaussian random loads
1
2018
... 全时域计算非常耗时,频域疲劳分析则相对简便. ABS规范给出了窄带响应下的疲劳损伤频域计算方法,Du等[7 ] 利用该方法计算了波浪载荷作用下的单桩基础海洋平台的疲劳损伤,并将其与时域分析结果对比,发现频域法计算的疲劳损伤是时域法结果的3.4倍. Mohammadi等[8 ] 认为ABS规范频域法计算结果过于保守的原因在于实际的应力幅概率分布并不严格符合ABS规范所假定的Rayleigh分布. 为此,一些学者提出适用于宽带过程的疲劳损伤分析方法[9 -12 ] . Benasciutti等[13 ] 研究了频域法的宽带过程疲劳问题,并讨论了带宽参数的取值与组合对疲劳损伤的影响. 双峰过程是宽带过程的1种特例[14 ] ,可由组合谱法[14 -17 ] 和疲劳损伤组合法[18 -20 ] 计算. ...
1
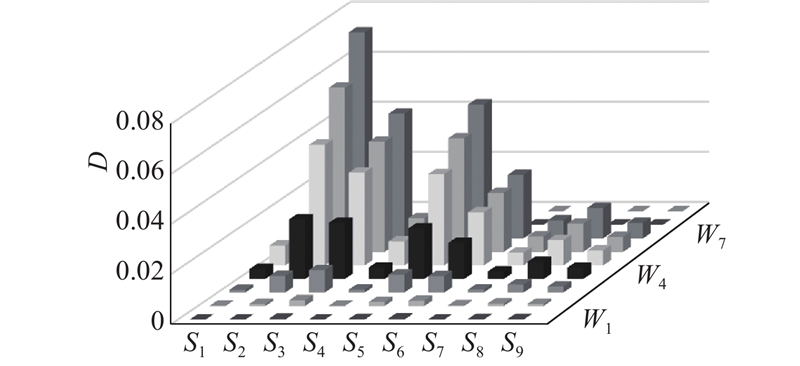
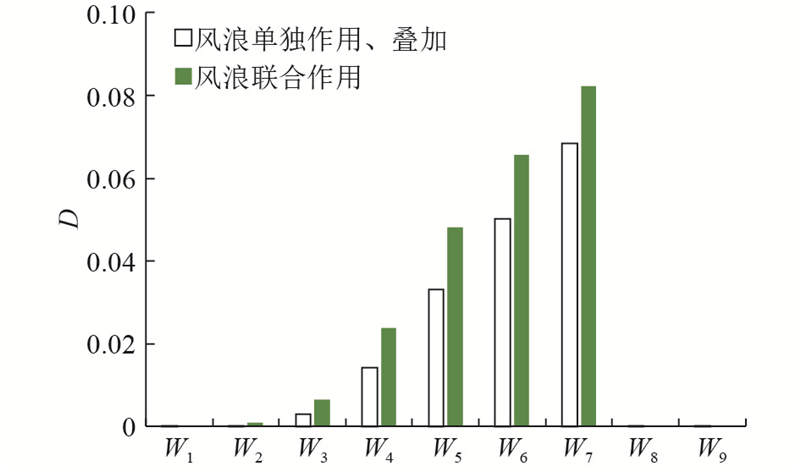
... 当前在海上风电结构疲劳设计时,为了简化载荷输入和减小计算量,通常的做法是分别计算风、浪单独作用时基础的疲劳损伤,再对损伤值进行叠加作为基础的总疲劳损伤. Yamashita等[21 ] 将海上单桩基础风机简化为多质点体系,计算表明风、浪联合作用的疲劳损伤比单独作用、损伤叠加得到的结果大25%. Dong等[22 ] 计算了导管架基础的疲劳损伤,结果表明疲劳损伤主要由风载荷引起,且考虑风、浪联合作用比单独作用计算得到的疲劳损伤大12.79%~24.60%. Yeter等[23 ] 采用频域方法分析了三桩式海上风机基础的疲劳损伤. Tempel[24 ] 分别采用时域和频域方法计算了海上风机基础疲劳损伤,发现由于2种方法得到的应力谱不同,损伤结果存在明显差异. Ziegler等[25 ] 采用频域方法分析了海上风机结构的浪致疲劳损伤,认为水深和波浪周期对浪致疲劳载荷具有显著影响. Marino等[26 ] 发现风机运行状态不同会有不同的气动阻尼,对疲劳损伤计算结果影响较大. 阻尼是一个非常复杂的因素,不同文献和风机运行工况的阻尼比取值差别较大,气动阻尼比取值范围在3%~9%[27 -28 ] ,材料阻尼比取值范围在0.19%~1.5%[29 -30 ] ,基础阻尼比取值范围在0.17%~1.3%[30 -31 ] . 由于实际风况和海况条件的复杂性,以及各海上风电文献所采用的风、浪载荷和计算参数不同,不同时域和频域计算方法之间难以相互验证和比较,难以评估不同方法之间的误差程度. ...
Long-term fatigue analysis of multi-planar tubular joints for jacket-type offshore wind turbine in time domain
1
2011
... 当前在海上风电结构疲劳设计时,为了简化载荷输入和减小计算量,通常的做法是分别计算风、浪单独作用时基础的疲劳损伤,再对损伤值进行叠加作为基础的总疲劳损伤. Yamashita等[21 ] 将海上单桩基础风机简化为多质点体系,计算表明风、浪联合作用的疲劳损伤比单独作用、损伤叠加得到的结果大25%. Dong等[22 ] 计算了导管架基础的疲劳损伤,结果表明疲劳损伤主要由风载荷引起,且考虑风、浪联合作用比单独作用计算得到的疲劳损伤大12.79%~24.60%. Yeter等[23 ] 采用频域方法分析了三桩式海上风机基础的疲劳损伤. Tempel[24 ] 分别采用时域和频域方法计算了海上风机基础疲劳损伤,发现由于2种方法得到的应力谱不同,损伤结果存在明显差异. Ziegler等[25 ] 采用频域方法分析了海上风机结构的浪致疲劳损伤,认为水深和波浪周期对浪致疲劳载荷具有显著影响. Marino等[26 ] 发现风机运行状态不同会有不同的气动阻尼,对疲劳损伤计算结果影响较大. 阻尼是一个非常复杂的因素,不同文献和风机运行工况的阻尼比取值差别较大,气动阻尼比取值范围在3%~9%[27 -28 ] ,材料阻尼比取值范围在0.19%~1.5%[29 -30 ] ,基础阻尼比取值范围在0.17%~1.3%[30 -31 ] . 由于实际风况和海况条件的复杂性,以及各海上风电文献所采用的风、浪载荷和计算参数不同,不同时域和频域计算方法之间难以相互验证和比较,难以评估不同方法之间的误差程度. ...
Fatigue damage assessment of fixed offshore wind turbine tripod support structures
1
2015
... 当前在海上风电结构疲劳设计时,为了简化载荷输入和减小计算量,通常的做法是分别计算风、浪单独作用时基础的疲劳损伤,再对损伤值进行叠加作为基础的总疲劳损伤. Yamashita等[21 ] 将海上单桩基础风机简化为多质点体系,计算表明风、浪联合作用的疲劳损伤比单独作用、损伤叠加得到的结果大25%. Dong等[22 ] 计算了导管架基础的疲劳损伤,结果表明疲劳损伤主要由风载荷引起,且考虑风、浪联合作用比单独作用计算得到的疲劳损伤大12.79%~24.60%. Yeter等[23 ] 采用频域方法分析了三桩式海上风机基础的疲劳损伤. Tempel[24 ] 分别采用时域和频域方法计算了海上风机基础疲劳损伤,发现由于2种方法得到的应力谱不同,损伤结果存在明显差异. Ziegler等[25 ] 采用频域方法分析了海上风机结构的浪致疲劳损伤,认为水深和波浪周期对浪致疲劳载荷具有显著影响. Marino等[26 ] 发现风机运行状态不同会有不同的气动阻尼,对疲劳损伤计算结果影响较大. 阻尼是一个非常复杂的因素,不同文献和风机运行工况的阻尼比取值差别较大,气动阻尼比取值范围在3%~9%[27 -28 ] ,材料阻尼比取值范围在0.19%~1.5%[29 -30 ] ,基础阻尼比取值范围在0.17%~1.3%[30 -31 ] . 由于实际风况和海况条件的复杂性,以及各海上风电文献所采用的风、浪载荷和计算参数不同,不同时域和频域计算方法之间难以相互验证和比较,难以评估不同方法之间的误差程度. ...
1
... 当前在海上风电结构疲劳设计时,为了简化载荷输入和减小计算量,通常的做法是分别计算风、浪单独作用时基础的疲劳损伤,再对损伤值进行叠加作为基础的总疲劳损伤. Yamashita等[21 ] 将海上单桩基础风机简化为多质点体系,计算表明风、浪联合作用的疲劳损伤比单独作用、损伤叠加得到的结果大25%. Dong等[22 ] 计算了导管架基础的疲劳损伤,结果表明疲劳损伤主要由风载荷引起,且考虑风、浪联合作用比单独作用计算得到的疲劳损伤大12.79%~24.60%. Yeter等[23 ] 采用频域方法分析了三桩式海上风机基础的疲劳损伤. Tempel[24 ] 分别采用时域和频域方法计算了海上风机基础疲劳损伤,发现由于2种方法得到的应力谱不同,损伤结果存在明显差异. Ziegler等[25 ] 采用频域方法分析了海上风机结构的浪致疲劳损伤,认为水深和波浪周期对浪致疲劳载荷具有显著影响. Marino等[26 ] 发现风机运行状态不同会有不同的气动阻尼,对疲劳损伤计算结果影响较大. 阻尼是一个非常复杂的因素,不同文献和风机运行工况的阻尼比取值差别较大,气动阻尼比取值范围在3%~9%[27 -28 ] ,材料阻尼比取值范围在0.19%~1.5%[29 -30 ] ,基础阻尼比取值范围在0.17%~1.3%[30 -31 ] . 由于实际风况和海况条件的复杂性,以及各海上风电文献所采用的风、浪载荷和计算参数不同,不同时域和频域计算方法之间难以相互验证和比较,难以评估不同方法之间的误差程度. ...
Sensitivity of wave fatigue loads on offshore wind turbines under varying site conditions
1
2015
... 当前在海上风电结构疲劳设计时,为了简化载荷输入和减小计算量,通常的做法是分别计算风、浪单独作用时基础的疲劳损伤,再对损伤值进行叠加作为基础的总疲劳损伤. Yamashita等[21 ] 将海上单桩基础风机简化为多质点体系,计算表明风、浪联合作用的疲劳损伤比单独作用、损伤叠加得到的结果大25%. Dong等[22 ] 计算了导管架基础的疲劳损伤,结果表明疲劳损伤主要由风载荷引起,且考虑风、浪联合作用比单独作用计算得到的疲劳损伤大12.79%~24.60%. Yeter等[23 ] 采用频域方法分析了三桩式海上风机基础的疲劳损伤. Tempel[24 ] 分别采用时域和频域方法计算了海上风机基础疲劳损伤,发现由于2种方法得到的应力谱不同,损伤结果存在明显差异. Ziegler等[25 ] 采用频域方法分析了海上风机结构的浪致疲劳损伤,认为水深和波浪周期对浪致疲劳载荷具有显著影响. Marino等[26 ] 发现风机运行状态不同会有不同的气动阻尼,对疲劳损伤计算结果影响较大. 阻尼是一个非常复杂的因素,不同文献和风机运行工况的阻尼比取值差别较大,气动阻尼比取值范围在3%~9%[27 -28 ] ,材料阻尼比取值范围在0.19%~1.5%[29 -30 ] ,基础阻尼比取值范围在0.17%~1.3%[30 -31 ] . 由于实际风况和海况条件的复杂性,以及各海上风电文献所采用的风、浪载荷和计算参数不同,不同时域和频域计算方法之间难以相互验证和比较,难以评估不同方法之间的误差程度. ...
Offshore wind turbine fatigue loads: the influence of alternative wave modeling for different turbulent and mean winds
1
2017
... 当前在海上风电结构疲劳设计时,为了简化载荷输入和减小计算量,通常的做法是分别计算风、浪单独作用时基础的疲劳损伤,再对损伤值进行叠加作为基础的总疲劳损伤. Yamashita等[21 ] 将海上单桩基础风机简化为多质点体系,计算表明风、浪联合作用的疲劳损伤比单独作用、损伤叠加得到的结果大25%. Dong等[22 ] 计算了导管架基础的疲劳损伤,结果表明疲劳损伤主要由风载荷引起,且考虑风、浪联合作用比单独作用计算得到的疲劳损伤大12.79%~24.60%. Yeter等[23 ] 采用频域方法分析了三桩式海上风机基础的疲劳损伤. Tempel[24 ] 分别采用时域和频域方法计算了海上风机基础疲劳损伤,发现由于2种方法得到的应力谱不同,损伤结果存在明显差异. Ziegler等[25 ] 采用频域方法分析了海上风机结构的浪致疲劳损伤,认为水深和波浪周期对浪致疲劳载荷具有显著影响. Marino等[26 ] 发现风机运行状态不同会有不同的气动阻尼,对疲劳损伤计算结果影响较大. 阻尼是一个非常复杂的因素,不同文献和风机运行工况的阻尼比取值差别较大,气动阻尼比取值范围在3%~9%[27 -28 ] ,材料阻尼比取值范围在0.19%~1.5%[29 -30 ] ,基础阻尼比取值范围在0.17%~1.3%[30 -31 ] . 由于实际风况和海况条件的复杂性,以及各海上风电文献所采用的风、浪载荷和计算参数不同,不同时域和频域计算方法之间难以相互验证和比较,难以评估不同方法之间的误差程度. ...
Fatigue life sensitivity of monopile-supported offshore wind turbines to damping
1
2018
... 当前在海上风电结构疲劳设计时,为了简化载荷输入和减小计算量,通常的做法是分别计算风、浪单独作用时基础的疲劳损伤,再对损伤值进行叠加作为基础的总疲劳损伤. Yamashita等[21 ] 将海上单桩基础风机简化为多质点体系,计算表明风、浪联合作用的疲劳损伤比单独作用、损伤叠加得到的结果大25%. Dong等[22 ] 计算了导管架基础的疲劳损伤,结果表明疲劳损伤主要由风载荷引起,且考虑风、浪联合作用比单独作用计算得到的疲劳损伤大12.79%~24.60%. Yeter等[23 ] 采用频域方法分析了三桩式海上风机基础的疲劳损伤. Tempel[24 ] 分别采用时域和频域方法计算了海上风机基础疲劳损伤,发现由于2种方法得到的应力谱不同,损伤结果存在明显差异. Ziegler等[25 ] 采用频域方法分析了海上风机结构的浪致疲劳损伤,认为水深和波浪周期对浪致疲劳载荷具有显著影响. Marino等[26 ] 发现风机运行状态不同会有不同的气动阻尼,对疲劳损伤计算结果影响较大. 阻尼是一个非常复杂的因素,不同文献和风机运行工况的阻尼比取值差别较大,气动阻尼比取值范围在3%~9%[27 -28 ] ,材料阻尼比取值范围在0.19%~1.5%[29 -30 ] ,基础阻尼比取值范围在0.17%~1.3%[30 -31 ] . 由于实际风况和海况条件的复杂性,以及各海上风电文献所采用的风、浪载荷和计算参数不同,不同时域和频域计算方法之间难以相互验证和比较,难以评估不同方法之间的误差程度. ...
Aerodynamic damping and seismic response of horizontal axis wind turbine towers
1
2014
... 当前在海上风电结构疲劳设计时,为了简化载荷输入和减小计算量,通常的做法是分别计算风、浪单独作用时基础的疲劳损伤,再对损伤值进行叠加作为基础的总疲劳损伤. Yamashita等[21 ] 将海上单桩基础风机简化为多质点体系,计算表明风、浪联合作用的疲劳损伤比单独作用、损伤叠加得到的结果大25%. Dong等[22 ] 计算了导管架基础的疲劳损伤,结果表明疲劳损伤主要由风载荷引起,且考虑风、浪联合作用比单独作用计算得到的疲劳损伤大12.79%~24.60%. Yeter等[23 ] 采用频域方法分析了三桩式海上风机基础的疲劳损伤. Tempel[24 ] 分别采用时域和频域方法计算了海上风机基础疲劳损伤,发现由于2种方法得到的应力谱不同,损伤结果存在明显差异. Ziegler等[25 ] 采用频域方法分析了海上风机结构的浪致疲劳损伤,认为水深和波浪周期对浪致疲劳载荷具有显著影响. Marino等[26 ] 发现风机运行状态不同会有不同的气动阻尼,对疲劳损伤计算结果影响较大. 阻尼是一个非常复杂的因素,不同文献和风机运行工况的阻尼比取值差别较大,气动阻尼比取值范围在3%~9%[27 -28 ] ,材料阻尼比取值范围在0.19%~1.5%[29 -30 ] ,基础阻尼比取值范围在0.17%~1.3%[30 -31 ] . 由于实际风况和海况条件的复杂性,以及各海上风电文献所采用的风、浪载荷和计算参数不同,不同时域和频域计算方法之间难以相互验证和比较,难以评估不同方法之间的误差程度. ...
1
... 当前在海上风电结构疲劳设计时,为了简化载荷输入和减小计算量,通常的做法是分别计算风、浪单独作用时基础的疲劳损伤,再对损伤值进行叠加作为基础的总疲劳损伤. Yamashita等[21 ] 将海上单桩基础风机简化为多质点体系,计算表明风、浪联合作用的疲劳损伤比单独作用、损伤叠加得到的结果大25%. Dong等[22 ] 计算了导管架基础的疲劳损伤,结果表明疲劳损伤主要由风载荷引起,且考虑风、浪联合作用比单独作用计算得到的疲劳损伤大12.79%~24.60%. Yeter等[23 ] 采用频域方法分析了三桩式海上风机基础的疲劳损伤. Tempel[24 ] 分别采用时域和频域方法计算了海上风机基础疲劳损伤,发现由于2种方法得到的应力谱不同,损伤结果存在明显差异. Ziegler等[25 ] 采用频域方法分析了海上风机结构的浪致疲劳损伤,认为水深和波浪周期对浪致疲劳载荷具有显著影响. Marino等[26 ] 发现风机运行状态不同会有不同的气动阻尼,对疲劳损伤计算结果影响较大. 阻尼是一个非常复杂的因素,不同文献和风机运行工况的阻尼比取值差别较大,气动阻尼比取值范围在3%~9%[27 -28 ] ,材料阻尼比取值范围在0.19%~1.5%[29 -30 ] ,基础阻尼比取值范围在0.17%~1.3%[30 -31 ] . 由于实际风况和海况条件的复杂性,以及各海上风电文献所采用的风、浪载荷和计算参数不同,不同时域和频域计算方法之间难以相互验证和比较,难以评估不同方法之间的误差程度. ...
Foundation damping and the dynamics of offshore wind turbine monopiles
3
2015
... 当前在海上风电结构疲劳设计时,为了简化载荷输入和减小计算量,通常的做法是分别计算风、浪单独作用时基础的疲劳损伤,再对损伤值进行叠加作为基础的总疲劳损伤. Yamashita等[21 ] 将海上单桩基础风机简化为多质点体系,计算表明风、浪联合作用的疲劳损伤比单独作用、损伤叠加得到的结果大25%. Dong等[22 ] 计算了导管架基础的疲劳损伤,结果表明疲劳损伤主要由风载荷引起,且考虑风、浪联合作用比单独作用计算得到的疲劳损伤大12.79%~24.60%. Yeter等[23 ] 采用频域方法分析了三桩式海上风机基础的疲劳损伤. Tempel[24 ] 分别采用时域和频域方法计算了海上风机基础疲劳损伤,发现由于2种方法得到的应力谱不同,损伤结果存在明显差异. Ziegler等[25 ] 采用频域方法分析了海上风机结构的浪致疲劳损伤,认为水深和波浪周期对浪致疲劳载荷具有显著影响. Marino等[26 ] 发现风机运行状态不同会有不同的气动阻尼,对疲劳损伤计算结果影响较大. 阻尼是一个非常复杂的因素,不同文献和风机运行工况的阻尼比取值差别较大,气动阻尼比取值范围在3%~9%[27 -28 ] ,材料阻尼比取值范围在0.19%~1.5%[29 -30 ] ,基础阻尼比取值范围在0.17%~1.3%[30 -31 ] . 由于实际风况和海况条件的复杂性,以及各海上风电文献所采用的风、浪载荷和计算参数不同,不同时域和频域计算方法之间难以相互验证和比较,难以评估不同方法之间的误差程度. ...
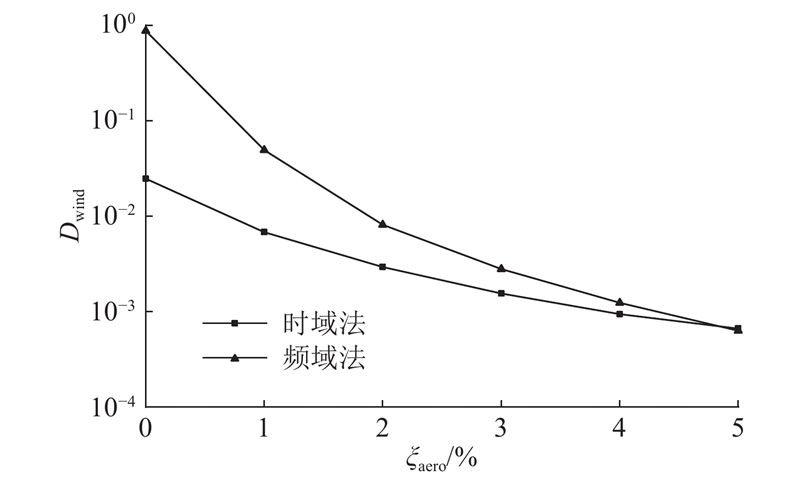
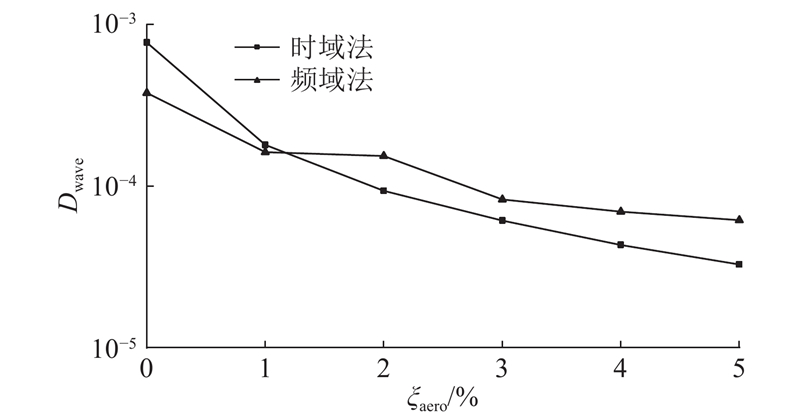
... [30 -31 ]. 由于实际风况和海况条件的复杂性,以及各海上风电文献所采用的风、浪载荷和计算参数不同,不同时域和频域计算方法之间难以相互验证和比较,难以评估不同方法之间的误差程度. ...
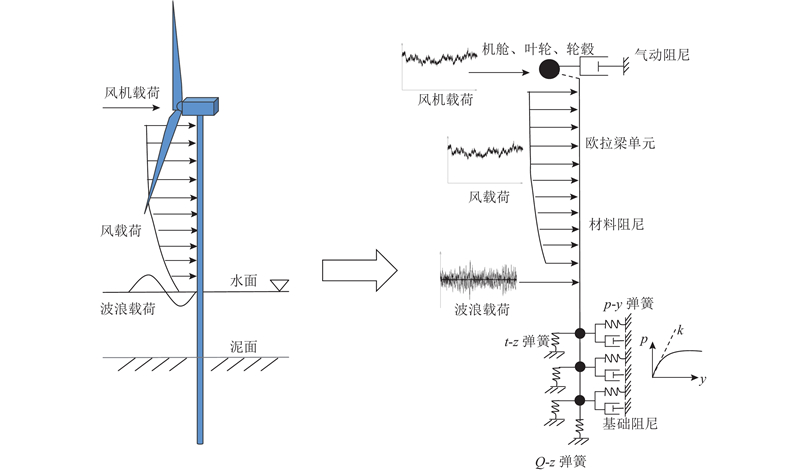
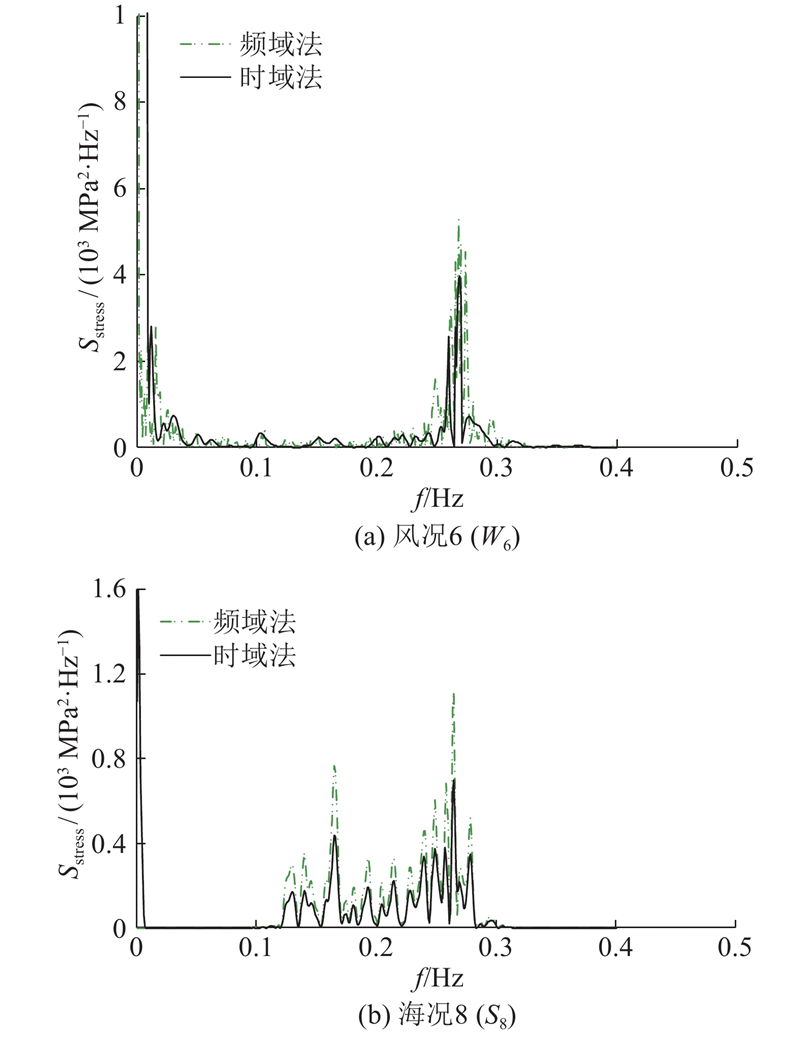
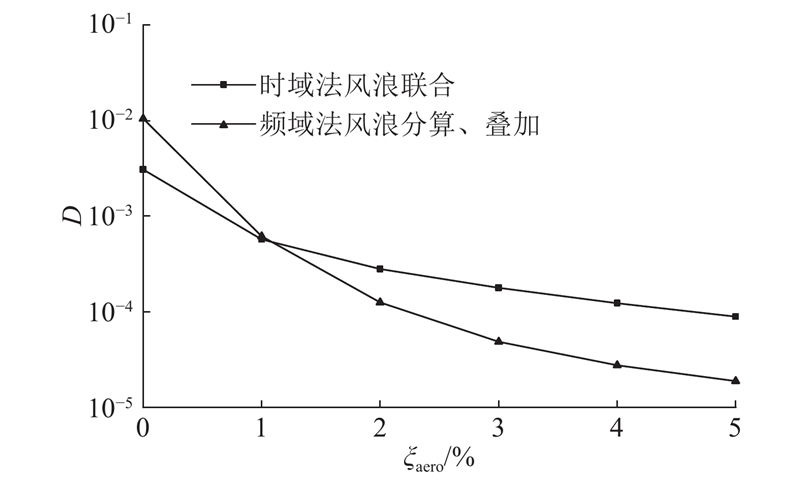
... 频域法的有限元模型与时域法相同,在稳态动力学分析步中进行谐响应分析,气动阻尼比ξ aero =3%,材料阻尼比ξ m =2%,基础阻尼比ξ fdn =3%[30 -31 ] ,分别得到风、浪载荷单独作用下计算点(本文计算点取基础−31 m截面处,下同)的应力传递函数(TRF). 在Matlab软件中计算各工况下风、浪载荷的功率谱密度函数(PSD). 由式(4)得到各工况下计算点的应力功率谱密度函数(PSD). 以风况W 6 和海况S 8 为例对比由频域法和时域法得到的应力谱,如图4 所示. ...
Cross-wind modal properties of offshore wind turbines identified by full scale testing
2
2013
... 当前在海上风电结构疲劳设计时,为了简化载荷输入和减小计算量,通常的做法是分别计算风、浪单独作用时基础的疲劳损伤,再对损伤值进行叠加作为基础的总疲劳损伤. Yamashita等[21 ] 将海上单桩基础风机简化为多质点体系,计算表明风、浪联合作用的疲劳损伤比单独作用、损伤叠加得到的结果大25%. Dong等[22 ] 计算了导管架基础的疲劳损伤,结果表明疲劳损伤主要由风载荷引起,且考虑风、浪联合作用比单独作用计算得到的疲劳损伤大12.79%~24.60%. Yeter等[23 ] 采用频域方法分析了三桩式海上风机基础的疲劳损伤. Tempel[24 ] 分别采用时域和频域方法计算了海上风机基础疲劳损伤,发现由于2种方法得到的应力谱不同,损伤结果存在明显差异. Ziegler等[25 ] 采用频域方法分析了海上风机结构的浪致疲劳损伤,认为水深和波浪周期对浪致疲劳载荷具有显著影响. Marino等[26 ] 发现风机运行状态不同会有不同的气动阻尼,对疲劳损伤计算结果影响较大. 阻尼是一个非常复杂的因素,不同文献和风机运行工况的阻尼比取值差别较大,气动阻尼比取值范围在3%~9%[27 -28 ] ,材料阻尼比取值范围在0.19%~1.5%[29 -30 ] ,基础阻尼比取值范围在0.17%~1.3%[30 -31 ] . 由于实际风况和海况条件的复杂性,以及各海上风电文献所采用的风、浪载荷和计算参数不同,不同时域和频域计算方法之间难以相互验证和比较,难以评估不同方法之间的误差程度. ...
... 频域法的有限元模型与时域法相同,在稳态动力学分析步中进行谐响应分析,气动阻尼比ξ aero =3%,材料阻尼比ξ m =2%,基础阻尼比ξ fdn =3%[30 -31 ] ,分别得到风、浪载荷单独作用下计算点(本文计算点取基础−31 m截面处,下同)的应力传递函数(TRF). 在Matlab软件中计算各工况下风、浪载荷的功率谱密度函数(PSD). 由式(4)得到各工况下计算点的应力功率谱密度函数(PSD). 以风况W 6 和海况S 8 为例对比由频域法和时域法得到的应力谱,如图4 所示. ...
1
... 平均风速沿高度方向的分布由风廓线描述,可由指数分布表示;认为平均风速长时间的概率分布满足威布尔分布. 通常假定脉动风是平稳的高斯过程,可以用功率谱的形式描述风在不同频率下的能量分布,常用的风谱包括Kaimal谱、Von Karman谱、Davenport谱等. 本文使用IEC标准[32 ] 中推荐的Kaimal谱来模拟脉动风速. ...
1
... 风作用在叶轮上的水平推力(风机载荷)由推力系数法确定,推力系数C T 由叶素-动量理论计算[33 ] . 为简化计算,本文只考虑顺风向的风载荷: ...
1
... 本文采用莫里森公式结合Pierson-Moscowitz波浪谱的方法计算波浪载荷[34 ] . ...