大范围参数的混沌系统是指在某个参数大范围变动下仍处于混沌状态的混沌系统,避免因参数的变更或误差改变系统动力学行为而使系统相轨收敛于不动点,或处于周期、拟周期和混沌的振荡状态. 贾红艳等[15]给出一个大范围的超混沌系统,参数范围为[10,1 000];梅蓉等[16]给出一类超大范围超混沌系统,仿真中给出的参数范围为[0,2 000].在确定的参数组合下,不同的初值组合导致系统的运行轨迹不同,一些运行轨迹最终收敛在同一个吸引子上,而有些运行轨迹收敛在其他吸引子上,称这些吸引子为共存吸引子. 有共存吸引子的混沌系统具有更复杂的动力学行为,并且由于共存吸引子的复杂性,系统在信息加密和保密通信领域具有较好的应用价值. 譬如,按某种伪随机方式选取初始值所得到的密钥对应于不同的混沌吸引域,增加了密钥破解的难度,从而提高了信息加密的安全性. Zhang[17]提出新颖的四维蝴蝶超混沌系统;史传宝等[18]提出有共存吸引子的三维连续混沌系统;雷腾飞等[19]构造了仅有1个线性项的有共存吸引子的三维连续自治混沌系统. 在已有关于大范围参数混沌系统的文献中,当系统参数在大范围内改变时,系统具有混沌吸引子,但没有共存的混沌吸引子.
在已有的大多数系统中,系统特性对系统参数的敏感性不强,即当系统参数发生微小改变时,系统的动力学特性变化较小. 在混沌保密通信中,系统特性对参数敏感性强意味着能得到更强的伪随机密钥,更有利于信息加密.
针对以上问题,本研究构建新型的混沌系统.基于Lorenz系统,通过改变其中的状态变量及其参数,构建当参数d在超大范围内变化时,2个孤立双翼混沌吸引子与1个四翼混沌吸引子均共存的混沌系统.通过对参数a做微小改变验证系统特性对参数a的敏感性;通过Multisim电路仿真,验证系统在硬件电路仿真方面的可实现性.
1. 系统模型与特性分析
1.1. 系统模型
参照Lorenz系统,新系统的数学模型为
式中:
图 1
1.2. 平衡点及其稳定性
令式(1)的左边等于0,即
求解式(2)得到5个平衡点分别为
系统在平衡点
令
式中:
当参数
表 1 新型混沌系统中平衡点的稳定性
Tab.1
| 平衡点 | 特征根 | 稳定性 |
| S0 | λ1=−3,λ2=−1为负实数;λ3=2为正实数 | 不稳定鞍点 |
| S1 | λ1=−3.114为负实数;λ2=0.557−2.239i,λ3=0.557+2.239i,均有正实部 | 不稳定的鞍焦点 |
| S2、S3 | λ1=−4.848为负实数;λ2=1.424−2.632i,λ3=1.424+2.632i,均有正实部 | 不稳定的鞍焦点 |
| S4 | λ1=−5.102为负实数;λ2=1.051−4.179i,λ3=1.051+4.179i,均有正实部 | 不稳定的鞍焦点 |
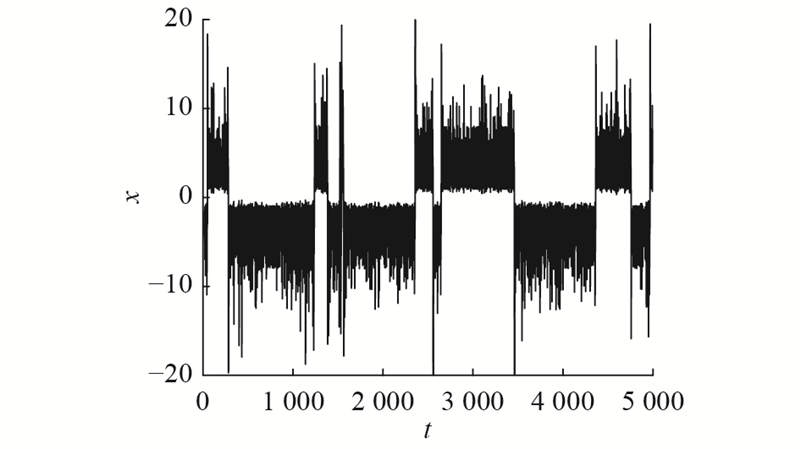
1.3. 时域波形图及Poincaré截面图
图 2
图 3
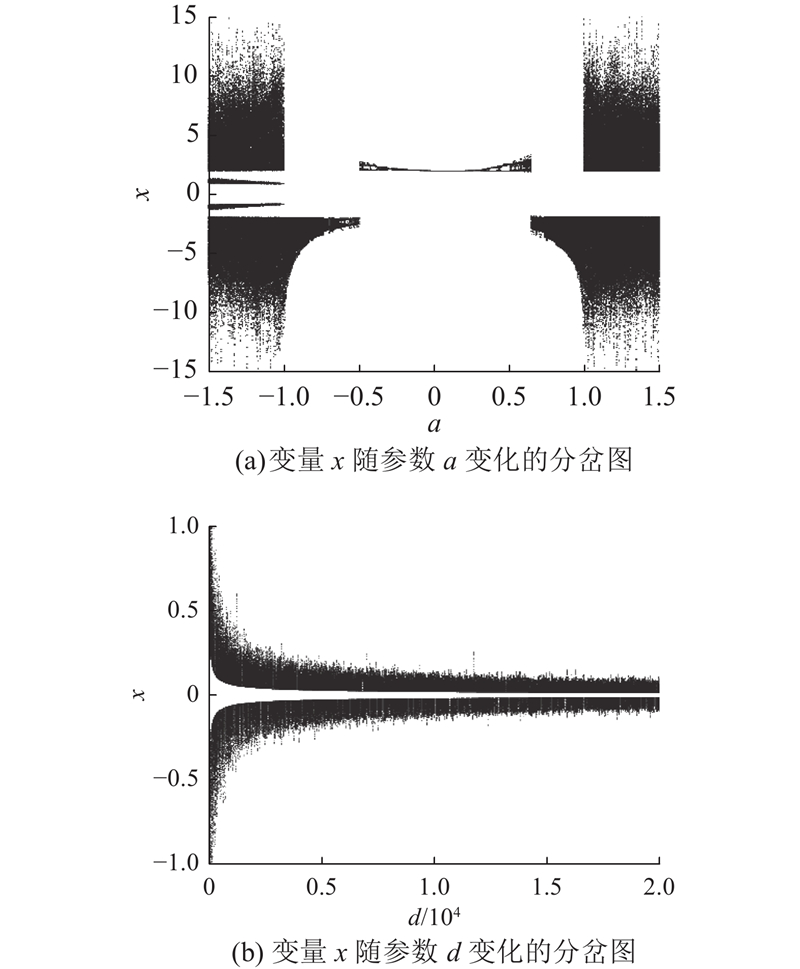
1.4. Lyapunov指数和Lyapunov维数
图 4
图 5
图 5 系统变量随参数变化的分岔图
Fig.5 Bifurcation diagrams of system variable with change of parameters
系统的Lyapunov维数表达式为
式中:j为常数;当
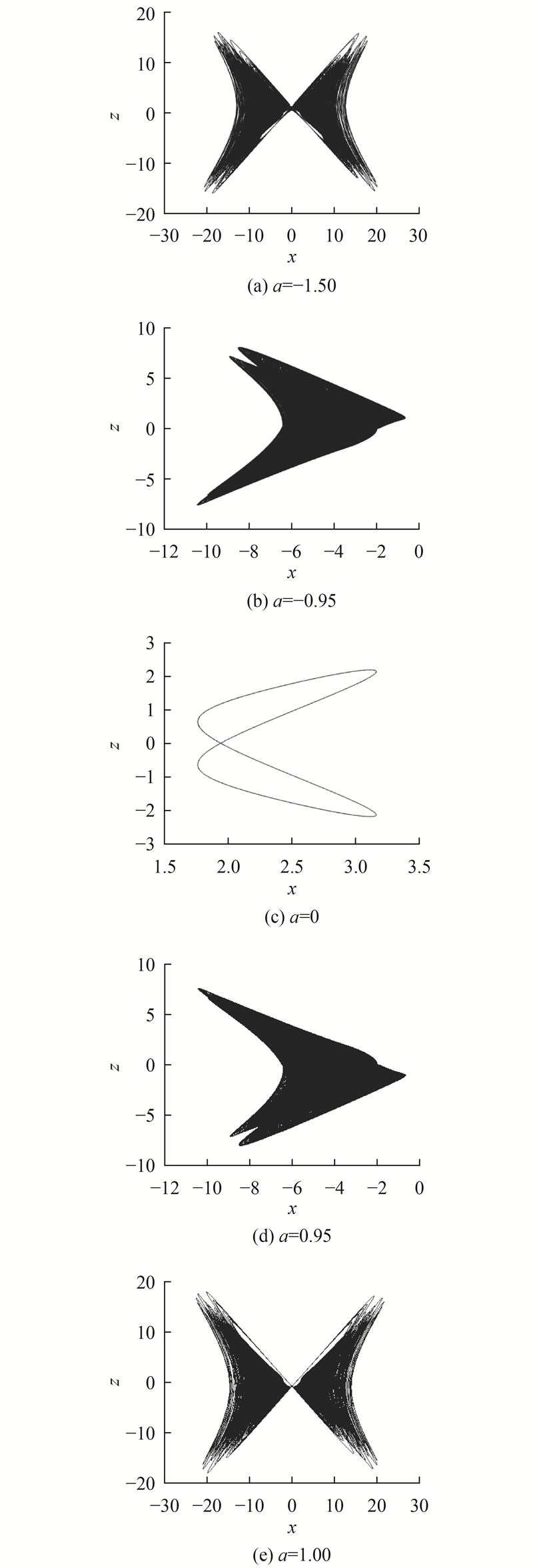
1.5. 系统参数的敏感性分析
图 6
图 6 不同参数a下系统的x-z相图
Fig.6 x-z phase diagrams for different values of parameter a
表 2
不同参数
Tab.2
| 参数a | Lyapunov指数 |
| a = −1.5 | 0.473 6, 0.007 2, − 2.480 9 |
| a = −0.95 | 0.296 9, −0.007 1, −2.289 8 |
| a = 0 | 0.004 2, −0.992 2, −1.012 0 |
| a = 0.95 | 0.316 3, −0.003 1, −2.313 2 |
| a = 1.00 | 0.395 1, 0.003 7, −2.398 8 |
2. 吸引子共存现象
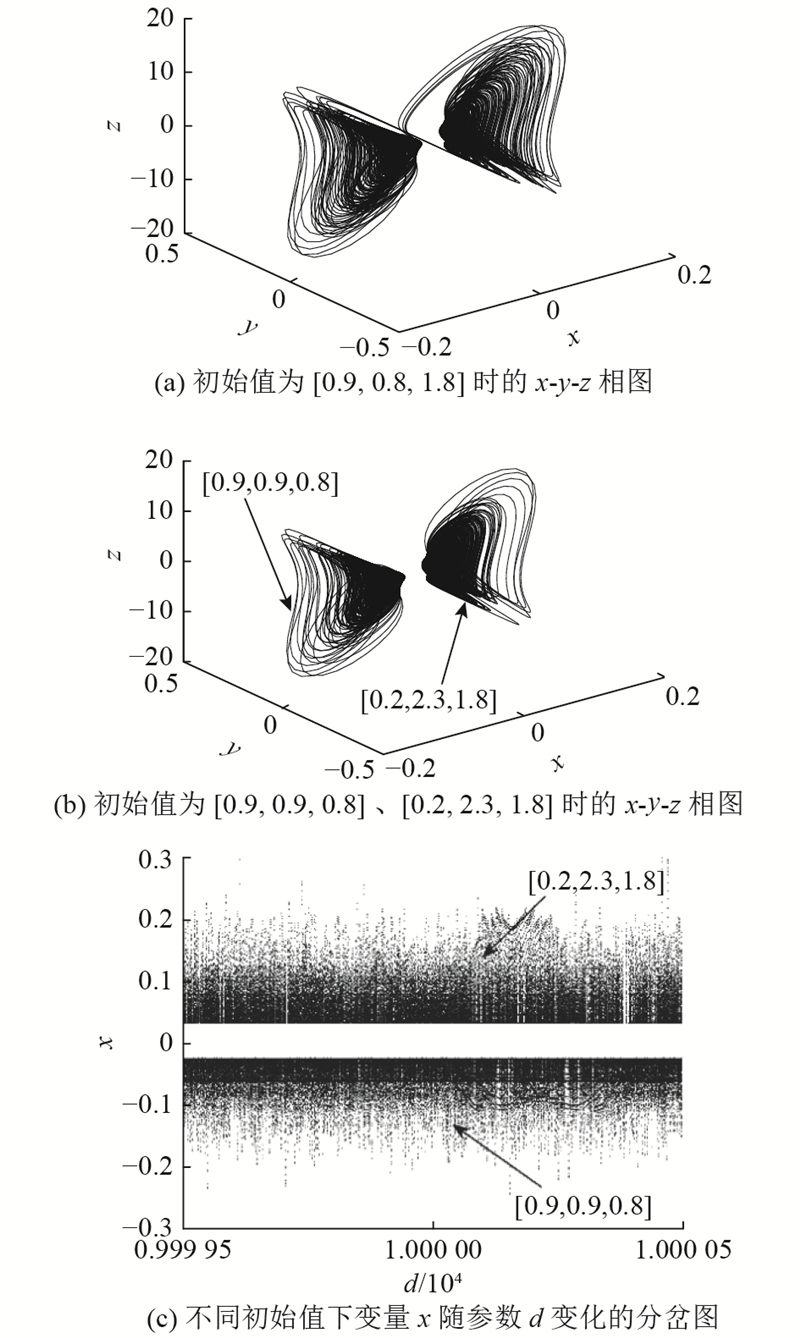
在系统参数确定的情况下,改变初始值,系统呈现出复杂的动力学变化,即2个孤立双翼混沌吸引子与1个四翼混沌吸引子共存的特性. 以x-y相图为例,当参数为
图 7
图 7 不同初始值对应的x-y相图及分岔图
Fig.7 x-y phase diagrams and bifurcation diagrams corresponding to different initial values
如图7所示,改变初始值的正负实现共存吸引子. 在实际应用中,改变正负意味着电源正负的转变,这无疑为电路实现增加了难度. 对于本研究构建的混沌系统,改变初始值的正负能够出现共存吸引子,不改变初始值的正负也能够出现共存吸引子,如图8(a)、(b)所示;选择
图 8
图 8 不同初始值对应的x-z相图及分岔图
Fig.8 x-z phase diagrams and bifurcation diagrams corresponding to different initial values
3. 超大范围参数下共存吸引子的存在性
图 9
图 9 d = 10时不同初始值对应的系统相图及分岔图
Fig.9 Phase diagrams and bifurcation diagrams corresponding to different initial values for d = 10
图 12
图 12 d = 10 000时不同初始值对应系统相图及分岔图
Fig.12 Phase diagrams and bifurcation diagrams corresponding to different initial values for d = 10 000
图 10
图 10 d = 100时不同初始值对应的系统相图及分岔图
Fig.10 Phase diagrams and bifurcation diagrams corresponding to different initial values for d = 100
图 11
图 11 d = 1 000时不同初始值对应的系统相图及分岔图
Fig.11 Phase diagrams and bifurcation diagrams corresponding to different initial values for d = 1 000
4. 混沌系统的电路仿真
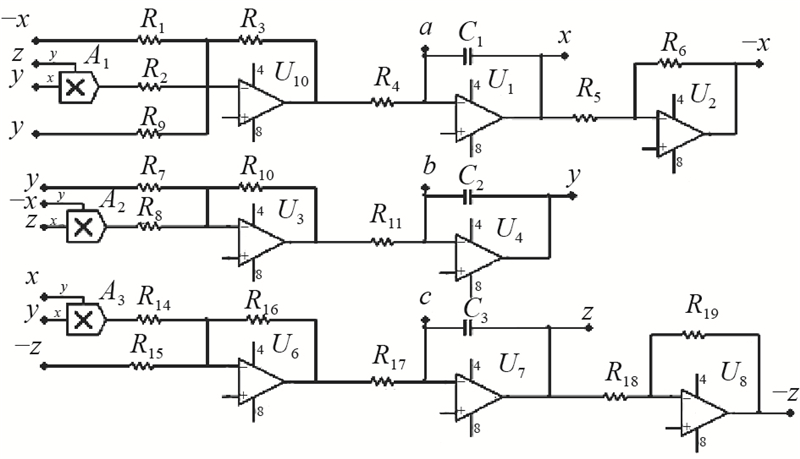
利用Multisim电路仿真软件,采用线性电阻、电容、LM2924N运算放大器、AD633模拟乘法器,实现该混沌系统的电路设计与模拟. 根据系统的动力学方程,设计电路原理图如图13所示. 其中乘法器的输出增益为0.1,通过改变电容和电阻,实现大范围混沌系统电路的模拟.
图 13
根据电路原理图,得到自激振荡电路表达式为
式中:R1~R11、R14~R17为电阻,C1~C3为电容. 取C1=C2=C3=1 uF,R4=R11=R17=1 kΩ,R5=R6=R18=R19=100 kΩ.
设
通过对比式(5)、(6),并保持相应系数相等,可以得到电阻为
求解可得
如图14所示为示波器上观察到的结果,可以看出当初始值为[0.1, 0.5, 1.7]、[0.5, 1.0, 1.0]、[0.8, 1.5, 1.5]时,实验结果与数值仿真结果完全相符.
图 14
对大范围参数下的多重共存吸引子进行电路仿真,如图15所示. 由于Multisim电路仿真软件精度及文章篇幅的原因,只给出当d=10、100、300时的电路仿真图,结果与Matlab仿真结果一致,证明在大范围参数下系统的3个共存吸引子的可实现性.
图 15
5. 结 语
构建的新型混沌系统中的参数d在超大范围
参考文献
基于动态混沌映射的三维加密正交频分复用无源光网络
[J].
Three-dimensional encrypted orthogonal frequency division multiplexing passive optical network based on dynamic chaotic mapping
[J].
一种基于混沌系统部分序列参数辨识的混沌保密通信方法
[J].DOI:10.3969/j.issn.1672-7940.2014.01.005
A chaotic secure communication method based on partial sequence parameter identification of chaotic system
[J].DOI:10.3969/j.issn.1672-7940.2014.01.005
Adaptive control of a chemical chaotic reactor
[J].
Deterministic nonperiodic flow
[J].
基于奇函数的一类四维四翼混沌系统设计与电路实现
[J].
Design and circuit implementation of a class of four-dimensional four-wing chaotic systems based on odd functions
[J].
Different families of hidden attractors in a new chaotic system with variable equilibrium
[J].
Dynamical analysis and electronic circuit realization of an equilibrium free 3D chaotic system with a large number of coexisting attractors
[J].
Nonlinear behavior of a novel chaotic jerk system: anti-monotonicity, crises, and multiple coexisting attractors
[J].
一类分数阶超混沌系统及其在扩频通信中的应用
[J].
A class of fractional hyper-chaotic systems and their applications in spread spectrum communication
[J].
一种具有隐藏吸引子的分数阶混沌系统的动力学分析及有限时间同步
[J].
Dynamic analysis and finite time synchronization of fractional order chaotic systems with hidden attractors
[J].
Generating one to four-wing hidden attractors in a novel 4D no-equilibrium chaotic system with extreme multistability
[J].
Generation of grid multi-scroll chaotic attractors via hyperbolic tangent function series
[J].
具有恒Lyapunov指数谱的新三维混沌系统分析与电路实现
[J].
Analysis and circuit implementation of a new three-dimensional chaotic system with constant Lyapunov exponent spectrum
[J].
A novel chaotic attractor with constant Lyapunov exponent spectrum and its circuit implementation
[J].
一个大范围超混沌系统的生成和电路实现
[J].DOI:10.3321/j.issn:1000-3290.2009.07.016 [本文引用: 1]
Generation and circuit implementation of a large-scale hyper-chaotic system
[J].DOI:10.3321/j.issn:1000-3290.2009.07.016 [本文引用: 1]
一类超大范围超混沌系统的动力学分析和电路实现
[J].
Dynamic analysis and circuit implementation of a class of super-large scale hyper-chaotic systems
[J].
A novel 4-D butterfly hyperchaotic system
[J].DOI:10.1016/j.ijleo.2016.11.083 [本文引用: 1]
一个新的混沌系统及其共存吸引子的研究
[J].
A new chaotic system and its coexistence attractor
[J].
一类具有吸引子共存新混沌系统的动力学分析、电路仿真及应用
[J].
Dynamic analysis, circuit simulation and application of a new chaotic system with attractor co-existence
[J].