在现代数字化装配环境下，对机械产品的装配质量有较高的要求. 产品大多由经过加工的各个零部件组装而成，其最终质量是制造系统中各种误差和缺陷综合作用的结果，因此组装过程中的质量控制对于保证最终产品的质量起到至关重要的作用. 复杂产品的组装须经过多道工序的装配，而每道工序上都存在一定的装配偏差. 在装配的各道工序上误差大小不同，种类也不同（零件制造误差、装配时的定位误差），各种误差随着装配的推进不断传递、累积和演化，导致最终产品的质量问题. 通过对复杂机械产品的装配过程进行偏差流建模，识别关键装配特征并对其误差源进行重点控制，这在数字化装配环境下对保证最终产品的质量具有重要意义.

传统对于装配质量的控制研究大多用于解决串行制造系统的偏差问题. 通过统计过程控制（statistical process control，SPC）理论^[1]对装配过程中的零部件质量进行分析，采集完备的测量数据实现对车身装配质量波动的监测. Hu等^[2]提出偏差流理论（stream of variation，SOV），该方法主要用于解决车身装配的质量监控问题，也被广泛应用于生产加工过程^[3-4]和装配过程^[5-6]的偏差建模与分析. 田兆青等^[7]借鉴状态空间方法，以零件偏差为状态矢量，夹具偏差为控制矢量，对多工位薄板的装配过程进行偏差流建模. 何博侠等^[8]以零件特征面为基本元素，集成三维中的位置和质量特征信息，结合机械装配偏差传递和累积的规律，建立装配过程状态空间模型，为偏差流控制的应用研究奠定了理论基础. Jin等^[9]首次运用状态空间理论对刚体零件在平面内运动造成的尺寸误差进行建模与分析，构建基于状态空间模型的偏差流控制模型. Ding等^[10]将状态空间模型的应用扩展到多阶段制造过程的建模与诊断过程中，描述离散时间线性时变随机系统，结合控制理论对多阶段制造过程进行质量控制. Mantripragada等^[11]提出基于状态转换模型方法的机械装配体中变异传播和控制算法，通过对单个零件的组合效应和装配方法的选择来确定和控制最终装配的变化. 张媛^[12]通过定义再制造装配过程马尔科夫链的一步转移概率矩阵建立基于马尔科夫链的待装零件分级选配模型，结合状态空间模型建立装配过程的偏差传递模型，实现对再制造装配过程的质量动态监控. Kantas等^[13]对基于状态空间模型的多阶段制造过程的质量控制方法进行了综述. 以上研究大多以状态空间模型以及偏差流理论为基础，结合其他相关质量分析方法对多阶段制造过程进行质量监控. 但是，状态空间模型的应用须采集大量数据，随着装配的进行须不断进行坐标数据转换，导致计算维度和复杂度较高、数据失真严重，因此状态空间模型较难有效应用于复杂多阶段装配过程的建模与分析.

目前，已有一些多阶段生产质量控制的典型方法被提出. 刘伟东等^[14]将刚性零件装配的偏差源分为集合位置偏差、几何形状偏差和装配位置偏差3类，结合多元统计学和偏差有向图理论，构建面向整个产品的偏差传递及装配功能表达的装配偏差有向图模型. 刘英等^[15]基于元动作理论对误差进行分类，引入误差链接模型，构建结构化误差关联模型并提出基于该模型的装配误差路径求解方法. 该方法的提出为整机装配过程的质量预测与控制提供了理论依据.

由于复杂网络理论可以用来描述信息量繁多的复杂系统，运用复杂网络能够清晰描绘出各种复杂系统的拓扑结构和统计特性. 复杂网络的相关网络特性可以反映出误差传递的路径和强度，符合装配工艺中的误差流传递特征，装配过程中的误差传递能由复杂网络模型详尽细致地描绘出来. Zhou^[16]基于复杂网络理论对回转类零件进行特征提取，为构建复杂网络奠定了基础. 高贵兵等^[17]提出基于复杂网络的制造系统脆弱性综合评估方法，将制造系统中的关键节点以及之间的对应关系对应于复杂网络的节点以及边，建立复杂网络模型，构造制造系统的脆弱性评估框架，并以发动机装配制造系统为例，对该系统的脆弱性进行分析. Boccaletti等^[18]结合动态簇系数分析将复杂网络分为不同模块，探究网络的模块度，符合加工系统中工序内节点关系紧密，工序间连接关系较为稀疏的特点，为误差溯源提供了新思路. Liu等^[19]提出基于偏差传递网络的加工误差源识别方法，建立工序间的波动方程，确定加工过程中须优先改进的工序. Jiang等^[20]将神经元模型和偏差传递网络相结合，实现多阶段加工系统质量的实时监控. Boccaletti等^[21]对复杂网络中的节点重要度排序方法进行综述，详细梳理了利用复杂网络中的各种统计特性进行排序的优劣性，为后续研究拓宽了视野. 目前，公开文献中还未有针对基于复杂网络的多工序装配过程偏差流建模方法的研究.

本研究针对多阶段装配系统，通过引入复杂网络的相关理论与方法，提出自调节赋权的偏差传递网络建模方法与误差源的逆向回溯算法，解决了多阶段装配系统的误差建模、识别、溯源等问题. 1）将装配过程中的各种关键表面抽象成特征节点，装配顺序抽象成连接关系，运用自调节赋权方法进行赋权，提出自调节赋权偏差传递网络；2）提出加权半局部中心性算法（weighted semi-local centrality algorithm，WSLCA）网络关键节点识别方法，识别多阶段装配过程中的关键装配面；3）提出逆向回溯算法，在网络模型中回溯误差传播路径，计算路径中节点的重要度排名（importance rank，IR），识别装配误差源；4）以具有代表性的锥齿轮组件的多阶段装配过程为实例进行建模与分析，验证本研究所提方法的有效性.

在机械产品的多阶段装配过程中，零件自身的加工误差会导致装配的精度偏差，装配时的定位误差也会导致最终产品的质量误差. 在各道装配工序中，误差的种类不确定，误差的大小也有差异，并且误差以特征表面为载体随着装配工序的推进，在零件间存在着传递、累积和演化关系（如某基准表面粗糙度误差会导致装配时结合面的定位误差）. 这些关系可以通过复杂网络赋权有向图的方式加以描述，因此复杂多阶段装配过程可以抽象为复杂系统，结合相关实测数据和装配工艺信息提取特征表面并进行赋权，形成装配过程的偏差传递赋权网络. 该网络模型可以反映偏差流的大小及传递路径.

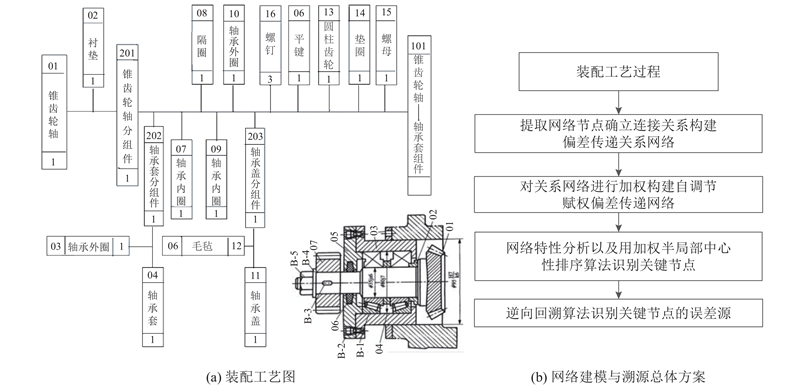
如图1（a）所示为某装配产品的装配工艺图，零部件的各个特征表面装配后会相互接触或结合. 不同零件上的误差会随着这种接触或者结合累积传递下去，反映为下一个零部件的装配误差，最终造成产品的装配质量误差. 在该产品装配工艺中，一个零件往往与其他多个零件相互接触，或与其他零件结合形成组件后进行后续装配，连接关系较为复杂. 可将各个零件中的关键接触表面抽象成网络节点，连接关系由装配工艺确定，该复杂系统可以由复杂网络进行建模与分析. 本研究所提出的网络建模与误差溯源方案如图1（b）所示，从装配工艺中提取网络节点和连接关系构建偏差传递关系网络，描述误差传递的方向和路径. 分别对不同的误差种类进行自调节赋权，形成自调节赋权偏差传递网络. 对网络进行特性分析并采用加权半局部中心性算法进行排序，确定网络的关键节点. 提出逆向回溯算法得到误差传递到关键节点的路径并采用重要度排名指标确定主要误差源，即须重点控制的装配过程.

多阶段装配过程中的误差一般分为2类，即零件加工误差导致的装配误差和零件装配时的基准或定位偏差导致的装配误差. 加工误差以加工特征为载体在装配路径中传递，加工特征为零件加工的基本单位，包括平面、圆、孔、槽等. 基准定位误差为装配结合位置相对于指定位置的偏差. 装配过程中的各个接触面相互影响，面与面之间互为基准进行定位，且误差的大小各不相同. 基于复杂网络构建的传统偏差传递关系网络只能反映误差传递的方向和路径，不能对误差传递的大小变化进行描述. 为了对误差进行全面细致的描述，须对关系网络进行赋权，使其能够对实际装配中的误差信息和网络动力学演化特征进行详尽描述.

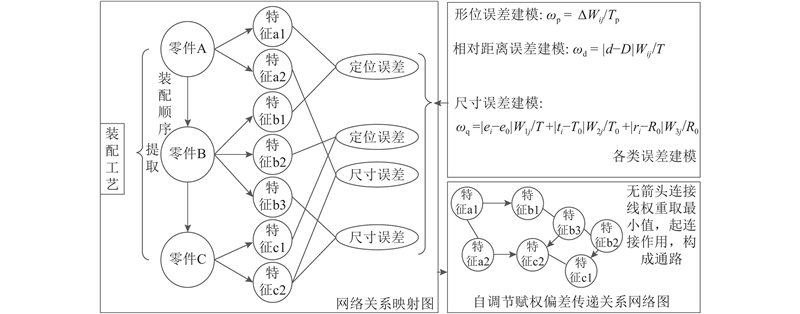
该网络中的节点是由加工工艺表中的相关信息抽象出来的参与装配的特征节点，根据装配顺序确定连接关系，再对连接关系进行赋权形成自调节赋权偏差传递网络. 详细建模过程如图2所示. 具体实施步骤如下.

1）提取特征节点，确定节点之间的连接关系. 根据组件的装配工艺表可以提取出加工过程中的关键装配特征节点（包括关键接触面的各个质量特征），通过对应的装配顺序，确定各个特征节点之间的连接关系. 连接关系有3种，即面与面的直接接触，面与面的相对距离，以面为基准进行的定位. 其中，面与面直接接触的连接关系是由于接触面上的加工误差导致误差的接触传递；面与面之间的相对距离的误差会影响组件的性能，导致组件质量受到影响；以面为基准进行定位的装配误差也会影响组件的最终性能. 连接关系都是从先安装面指向后安装面. 通过装配对应关系连接特征节点，从而构建偏差传递关系网络. 偏差传递关系网络可以定义为 $G = \{ < {v_i},{v_j} > ,{\omega _{ij}}\} $， ${v_i}$、 ${v_j}$为网络中的节点， ${\omega _{ij}}$为两节点连接的初始权重，若节点 ${v_i}$、 ${v_j}$之间有连接，则 ${\omega _{ij}}$=1，否则为0.

2）为网络连边赋权，确定误差传递因子. 在关系网络构建后要对各个节点之间的相互影响强度进行赋权，须对各个节点之间的误差传递强度进行建模. 对应节点之间的3种连接关系，误差权重的3种计算方式如下.

a）面与面之间直接接触. 接触面之间的相互影响可以细化为接触面上的质量特征的相互影响，面上的质量特征包括尺寸、形位以及粗糙度. 定义尺寸误差、形位误差、粗糙度误差分别为 ${\varepsilon _{\rm S}}$、 ${\varepsilon _{\rm L}}$、 ${\varepsilon _{\rm R}}$，有

(1) $ {\varepsilon _{\rm S}} = {{\left| {{e_{{i}}} - {e_0}} \right|{W_{{{1j}}}}} / T}. $

式中： ${e_{{i}}}$为i节点的实际测量尺寸； ${e_0}$为额定尺寸； $T$为该特征尺寸的允许变动公差； ${W_{1j}}$表示节点i的尺寸误差是否对节点j造成了影响，若有影响则取1，否则为0，下同.

(2) $ {\varepsilon _{\rm L}} = \left| {{t_{{i}}} - {T_0}} \right|{W_{{{2j}}}}/{T_0}. $

式中： ${t_{{i}}}$为i节点的实际形位指标， ${T_0}$为加工的形位要求.

表面特征描述了零件加工表面的粗糙度、热处理特性等. 以主要因素粗糙度误差作为表面特征误差.

(3) $ {\varepsilon _{\rm R}} = \left| {{r_{{i}}} - {R_0}} \right|{W_{{{3j}}}}/{R_0}. $

式中： ${r_{{i}}}$为i节点实际测得的加工表面粗糙度， ${R_0}$为加工粗糙度要求. 最终加工特征之间的权重因子为

(4) $ {\omega _{\rm q}} = {\varepsilon _{\rm S}} + {\varepsilon _{\rm L}} + {\varepsilon _{\rm R}}. $

b）面与面之间的相对距离. 相对距离误差的表达式为

(5) $ {\omega _{\rm d}} = \left| {d - D} \right|{W_{ij}}/T. $

式中： $d$为两面之间的实际距离； $D$为两面之间要求的距离； $T$为两面之间距离的范围公差； ${W_{{{ij}}}}$表示节点i、j之间是否有距离要求，若有为1，否则为0.

c）以面为基准进行定位安装. 该误差的表达式为

(6) $ {\omega _{\rm{p}}} = \varDelta {W_{{{ij}}}}/{T_{\rm{p}}}. $

式中：Δ为实际测得位置与要求位置的偏差， ${T_{\rm{p}}}$为实际位置允许距离要求位置的变动公差.

通过对偏差传递关系网络进行赋权形成自调节加权偏差传递网络，最终网络可以表示为 $G = \{ V,E,W\} $，其中 $V = \{ {v_1},{v_2},{v_3},\cdots,{v_n}\} $为节点集， $E = \{ {e_1},{e_2},{e_3},\cdots,{e_m}\} $为边集， $W = \{ {\omega _1},{\omega _2},{\omega _3},\cdots,{\omega _m}\} $为边的权重集合.

复杂网络中的关键节点是指相较于网络中的其他节点能在更大程度上影响网络性能与网络结构的节点. 通过对关键节点进行重点监控能保证整个装配网络的稳定，即控制装配过程中的关键装配表面的质量可以保证装配线的正常运行. 因此，识别误差传播网络中的关键节点对确保产品的装配质量具有重要意义.

首先对偏差传递关系网络进行相关特性分析，运用常规识别关键节点的方法对其进行辨别，如节点度、度分布、平均路径长度、介数、簇系数等. 用对应的节点强度和加权聚集系数等特性分析方法对加权偏差传递网络的结构特性进行分析. 这些特性分析可以在不同方面反映各个节点在网络中的重要程度，再结合加权半局部中心性算法对赋权网络进行分析，确定装配网络中的重要加工节点. 如表1所示为复杂网络中特性分析的常用计算方法^[21].

借鉴半局部中心性算法对节点重要性进行有效排序，该排序算法涉及了节点的四阶邻居信息，能更好地基于全局信息对网络进行分析. 该算法的计算复杂度随网络规模线性增长，消耗较少的计算时间就能获得优于度中心性和介数中心性的排序结果^[22]. 在一定程度上半局部中心性算法优于PageRank算法^[23]和LeaderRank算法^[24]，并且计算复杂度最低. 定义 $N({{w}})$为节点 ${{w}}$的两层邻居度，等于从节点 ${{w}}$出发2步能到达的邻居节点数. 令

(7) $ Q(j) = \sum\limits_{{{w}} \in \varGamma (j)} {N({{w}})} . $

式中： $\varGamma (j)$为节点 ${v _j}$的一阶邻居节点集合. 节点 ${v _i}$的局部中心性表达式为

(8) $ {\rm{SLC}}(i) = \sum\limits_{{{w}} \in \varGamma (i)} {Q({{w}})} . $

该排序算法能较好地刻画网络中节点的重要性，但是未充分考虑到偏差传递网络中传递的误差大小是各不相同的，结果可能与真实情况存在偏差. 本研究对半局部中心性算法进行改进，不仅考虑邻居节点的数量，还考虑各个节点的权重对误差传播的影响. 所提出的加权半局部中心性算法表达式为

(9) $\left.\begin{aligned} &{\rm{WSLCA}}(i) = f({v _i})\sum\limits_{j \in \varGamma (i)} {(k_j^{\rm{out}} + 1)}\,,\\ &\quad\quad f({v_i}) = {10^{ - {c_i}}}{\rm{ES}}_i^{\rm{out}}\, .\end{aligned}\right\} $

式中： $k_j^{\rm{out}}$为节点j的出度，即从节点j出发指向外部节点的个数； $f({v _i})$为节点 ${v _i}$的权重函数； ${c_i}$、 ${\rm{ES}}_i^{\rm{out}}$分别为节点i的聚集系数和出强度（见表1）. 聚集系数越大，该节点的影响范围越小；节点的出强度越大，该节点对网络的影响越大；节点i的聚集系数越小且出强度越大，则 $f({v _i})$越大. 结合网络特性分析结果和加权半局部中心性排序算法对网络进行排序，确定网络的关键节点.

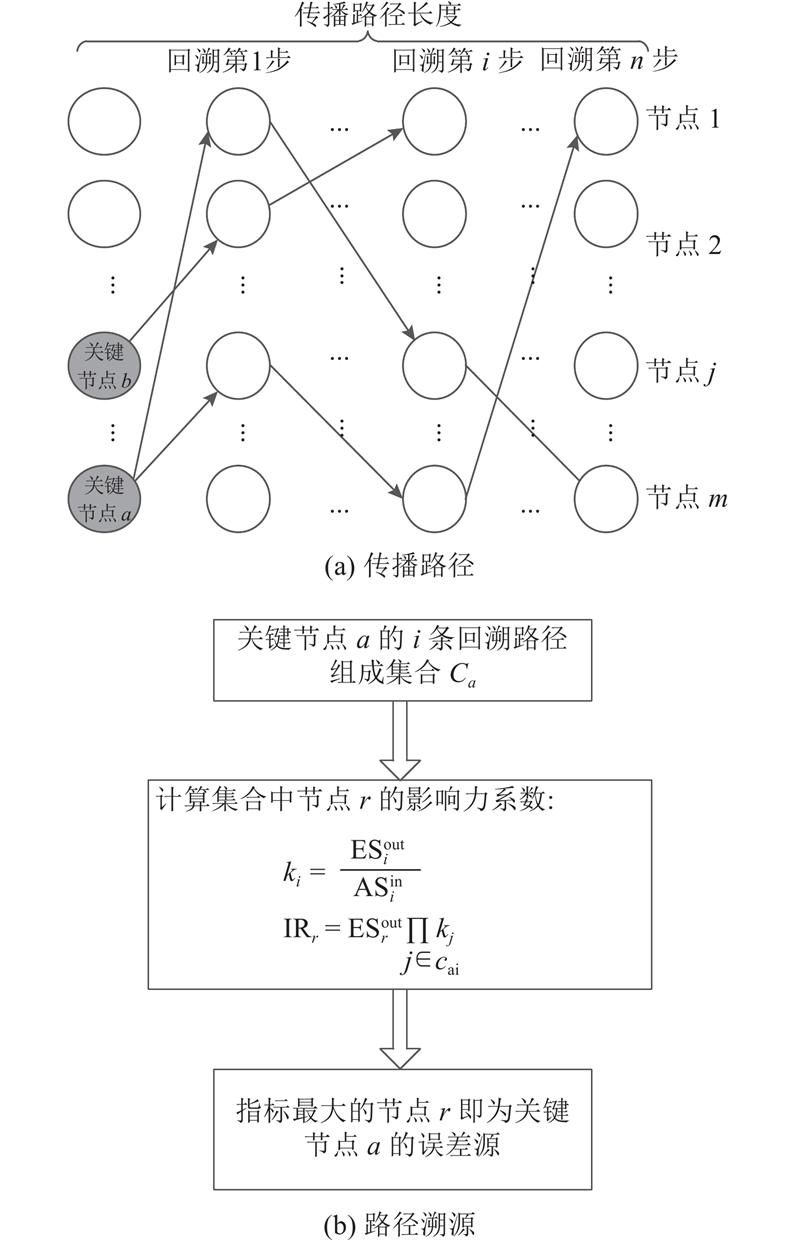
在采用加权半局部中心性算法识别关键装配节点后，为了保证整个装配过程的质量，须对关键节点的质量进行重点监控. 分别对关键节点的误差源头进行控制才能有效控制误差传播，同时减少误差控制的成本，因此，对关键节点进行误差溯源具有重要意义. 在装配网络中，节点间相互连接，2个节点之间可能存在不止1条通路，即1个关键特性可能受到多个误差源的影响. 通过逆向回溯算法和IR指标可以得到对目标关键节点影响最大的节点，该节点即为误差源节点，误差源节点可能有1个或者多个，在具体生产过程中往往结合生产策略选取影响最大的源节点进行控制，以保证生产的质量稳定.

如图3所示为本研究所提出的误差溯源方法. 如图3（a）所示为回溯关键节点误差路径的方法，其中的列为网络的所有节点，从左至右的箭头指向每一步回溯所经过的节点. 例如，关键节点a的回溯路径为节点a→节点1→节点j→节点m，节点a→节点j→节点m→节点1，则误差传播路径为节点m→节点j→节点1→节点a，节点1→节点m→节点j→节点a，即关键节点a回溯的所有路径中的节点组成了集合 ${C_a}$. 为了保证误差溯源的精度，仅计算回溯3步以内的路径.

提出基于IR指标的判别方法对集合 ${C_a}$中的节点的影响度进行计算. 基本思想如下：节点i的波动系数用i点的出强度与i点的入强度 $ {\rm{AS}}^{\rm{in}}_i$的比值k来衡量，表示节点i受到影响后对后续节点的影响能力. 表达式为

(10) $ {k_i} = \frac{{{\rm{ES}}_i^{\rm{out}}}}{{{\rm{AS}}_i^{\rm{in}}}} = \frac{{\sum\limits_{j \in {N_i}} {{\omega _{ij}}{a_{ij}}} }}{{\sum\limits_{j \in {N_i}} {{\omega _{ji}}{a_{ij}}} }}. $

式中： ${\omega _{ij}}$为节点 $i$对节点 $j$的影响权重， ${a_{ij}}$表示节点 $i$、 $j$之间是否有权重连接. 集合 ${C_a}$的路径 $i$中的节点r的影响力的计算思想为以r点作为源头，其误差强度经过传播路径中节点的传播到达关键节点. 路径中各个节点的传播系数为受到影响后的波动系数，波动系数的表达式为

(11) $ {\rm I}{{\rm R}_r} = {\rm{ES}}_r^{\rm{out}}\prod\limits_{j \in {c_{ai}}} {{k_j}} . $

式中： ${\rm{ES}}_r^{\rm{out}}$为节点 $r$的出强度， ${c_{ai}}$为集合 $C_a $中第 $i$条路径， $j$为在路径 $i$中从待溯源的目标节点 $r$到关键节点之间的所有节点，包括 $r$. 经过计算确定集合 ${C_a}$的节点中IR最大的节点，该节点即为关键节点 $a$的误差源节点. 只须对误差源节点的质量进行重点监控就能保证关键节点的质量，从而保证整个装配路线的正常运作.

为了验证所提出的针对多阶段装配系统的偏差传递建模以及误差溯源方法的有效性，选用具有代表性的锥齿轮轴组件的多阶段装配过程为研究对象. 锥齿轮轴组件是减速器的重要组成部分，该部分可以独立进行组装之后再整体装入箱体，其余2个组件均须在部件总装时与箱体一起装配. 为了防止箱体内润滑油渗漏及灰尘进入机体内，且组件上各零件之间也有相对位置要求，对于该产品部件装配的精度有较高要求.

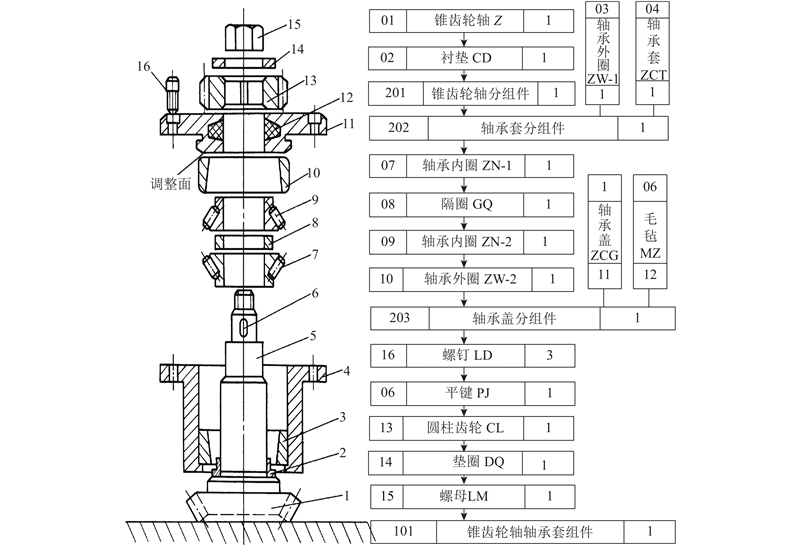
该组件的装配示意图以及装配工艺如图4所示. 图中对各个零件进行了编号，以零件名称的音译大写字母作为零件代号. 每个零件上又有多个特征，根据装配的先后接触顺序在零件代号后添加相应的序号表示零件的特征节点，如CD-1表示衬垫内径，CD-2表示衬垫外径. 可以看出，该组件由13个零件装配而成，在连接关系上面与面的接触占主要部分. 由装配的顺序关系可知，前列装配面造成的误差会导致后续装配的误差，因此误差在零件间会传递和累积. 以面为基准的装配误差会导致误差的演化，即从面的制造误差演化为相对距离误差等. 该组件的装配过程中的误差传递相对复杂，可以用复杂网络对其进行偏差建模分析.

每个零件在装配过程中会与其他零件有很多的接触面，因此可以将单个零件根据装配信息抽象成不同的特征节点. 比如轴承内圈的特征节点有上下接触面以及圆径. 同一个零件上的特征节点之间存在着连接关系，这种连接关系的强度取最小计数值，以保证整个网络的连接性而又不影响节点的重要性. 根据装配工艺信息提取出相关的特征节点，共有61个. 利用装配顺序可以确定相应的连接关系是从先安装面指向后安装面，从而确定整个网络的连接关系. 结合第2章中提出的赋权公式（式（1）~（6）），对偏差传递关系网络中的3种连接关系进行赋权，进而生成加权偏差传递网络. 该网络的拓扑模型如图5所示，图中节点的大小正比于节点的度，即节点的邻居节点越多节点就越大. 对节点Z-1进行放大（见图5右侧），该节点以不同的权重影响着众多其他节点，该节点可能在网络中占据重要地位.

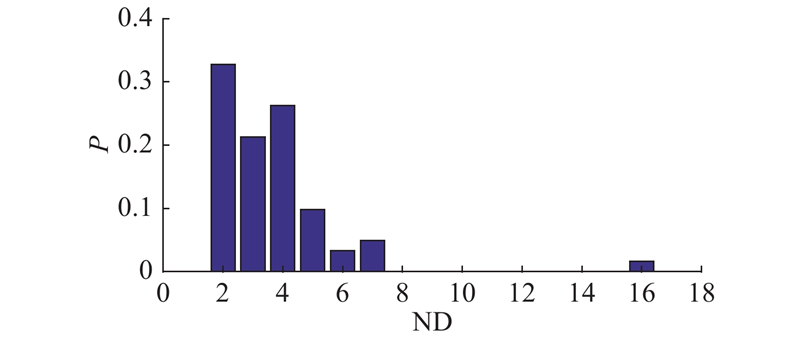
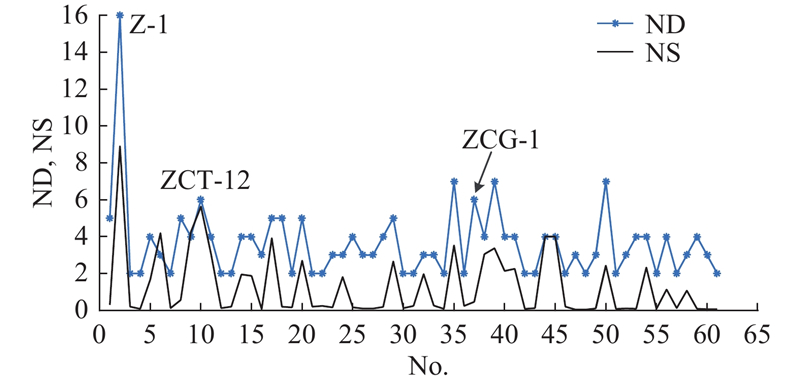
采用表1中的计算方法对加权偏差传递网络进行特性分析，包括节点度、节点介数、簇系数等相关网络特性. 如图6所示为网络的节点分布图. 图中，ND为节点度大小，P为所占比例. 可以看出，网络中大部分节点的度都在一定的范围内而少数节点具有较大的度. 通常来说，某节点具有较大的度说明该节点能影响的邻居节点的个数较多，因此该类少数节点可能在网络中起重要作用. 如图7所示，将偏差传递网络中各节点的度和强度绘制在一张图上进行比较. 图中，No. 为网络节点序号，NS为节点强度. 可以看出，一般情况下具有较大度的节点也具有较大的节点强度，如Z-1（轴1外径）和ZCT-12（轴承套内径2），说明此类节点在网络中可能占据重要地位，即不仅能够影响较多的邻居节点并且具有一定的影响强度. 节点ZCG-1（轴承盖下底面）虽然有较大的节点度，但是其节点强度较小，因此该类节点传播误差的效应较低.

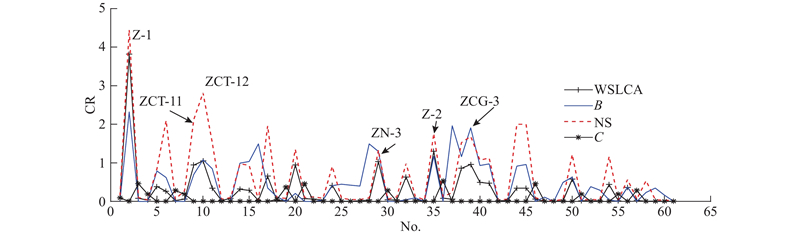
为了进一步确定网络中的关键节点，对偏差传递网络的相关特性，包括介数、节点强度以及簇系数进行分析，并用改进的加权半局部算法进行计算. 运用式（9），先计算每个节点的权重 $f({v _i})$，再计算其邻居节点的出度，进而求得各个节点的WSLCA，分析结果如图8所示. 图中，CR为经过等比例缩放后，对节点重要性进行判别的指标. 可以看出，加权半局部算法较符合节点强度和介数的分析结果. 节点Z-1，ZCT-11（轴承套内径1），ZCT-12，ZN-3（轴承内圈2内径）等具有较大的WSLCA的同时也具有较大的介数B和节点强度NS，说明该类节点在赋权偏差传递网络中占据重要地位，是关键节点. 簇系数C主要描述节点的聚集程度，而在装配网络中节点之间的连接方式是按照装配顺序依次连接的，较少会出现节点聚集的现象，因此在该装配偏差传递网络中簇系数不作为重要节点判别的重要依据. 最终确定的关键节点为Z-1、ZCT-11、ZCT-12、ZN-3、Z-2、ZCG-3（轴承盖内径）.

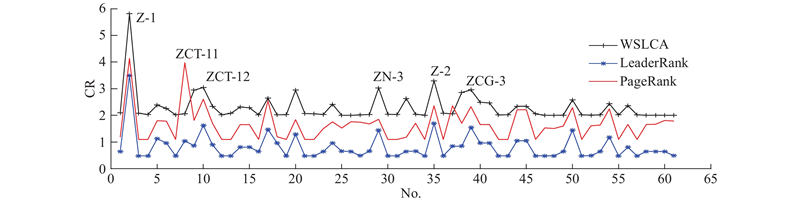
如图9所示，将本研究所提出的WSLCA算法和目前复杂网络中通用的网络节点重要性评价方法（PageRank以及加权LeaderRank算法）进行比较. 可以看出，3种算法对于网络中关键节点的评判大体一致. PageRank算法为整个网络引入随机跳转概率参数，导致节点的随机跳转概率相同，而实际偏差传递网络中的误差大小权重不同. 加权LeaderRank算法是Pagerank的优化算法，用一个全连接的背景节点替代PageRank中引入的随机跳转概率参数，形式上更加优美，也能更快达到收敛. 在3种算法得到的结果中，节点Z-1、ZCT-12、ZN-3、Z-2、ZCG-3的重要度系数均较大. 相比之下，WSLCA算法识别出节点ZCT-11也具有较大的重要度系数，因为该算法考虑了邻居节点的出度，ZCT-11节点的邻居节点ZCT-12等对网络的影响程度较大，因此ZCT-11节点也具有较大的IR. 综上，WSLCA算法能够弥补PageRank以及LeaderRank算法的不足，对整个装配网络的关键节点进行有效识别.

识别装配过程中的关键节点只是确定了某个部件上某个加工特征或者关键表面的重要性. 为了进一步从源头控制装配偏差，须对关键节点的误差进行溯源，识别导致关键节点质量失控的误差源，并对其进行质量控制. 具体步骤如下.

1）确定关键装配表面. 根据3.2节中的特性分析以及改进的加权半局部算法，确定该装配网络中的关键装配表面为Z-1、ZCT-11、ZCT-12、ZN-3、Z-2、ZCG-3.

2）回溯误差传递路径. 根据误差路径的逆向回溯算法查找出每个关键节点的回溯路径的集合. 以关键节点ZCG-3为例，在表2中查找误差传递到节点ZCG-3的传播路径. ZCG-3节点所在列中的数字若不为零则表示ZCG-3受到了误差影响，数字大小为受到的影响程度的大小，误差节点为非零元素所在的横坐标，即Z-2、ZCG-2，则节点Z-2、ZCG-2为逆向回溯算法第1步路径找到的节点；查找回溯的第2步节点时须观察第1步中的节点，遍历ZCG-2列的非零元素对应的横坐标，为ZCT-3、ZCT-1；回溯误差路径第3步时须观察第2步中的节点，同理，分别遍历ZCT-3、ZCT-1列的非零元素，对应的横坐标则为第3步的节点. 由此可以得到节点ZCG-3的逆向回溯路径，如表3所示.

3）计算路径中节点的IR，确定关键节点的误差源. 经由步骤2）得到了误差传播路径，对路径中的节点运用式（11）进行计算，得到路径中各个节点的误差影响力排名，如表4所示. 节点Z-1、ZCT-12（轴承套内径2）的IR最大，因此节点ZCG-3的主要误差源为节点Z-1、ZCT-12. 同理，对关键节点Z-1、ZCT-11、ZCT-12、Z-2进行误差溯源. 如表5所示为计算得出的各个关键节点的误差源. 可以发现，关键节点Z-1不仅是关键节点，同时也是大多数其他关键节点的误差源节点，因此须对关键装配表面Z-1（轴1外径）进行重点控制. 此外须对关键装配表面Z-0（锥齿轮轴底面）、CD2（衬垫外径）、ZCT-11（轴承套内径1）进行重点控制.

结合实际分析，锥齿轮轴组件的轴是连接各个分部件的中心，其中装配面轴1外径与不同的零部件接触更多，若该装配表面出现误差，会对装配质量造成重大影响. 轴承套内径、轴承内圈2内径以及衬垫的外径这3个质量特征为组件内部的重要参数，会影响装配的密封性等要素，对后续装配的质量也有一定的影响. 可以看出，本研究所提出的方法可以对复杂多阶段装配过程进行有效的偏差传递建模、关键节点识别以及误差溯源.

（1）运用复杂网络理论，结合实际装配工艺过程提取特征节点构建误差传递关系网络，利用相关实测数据与自调节误差赋权模型对关系网络赋权，有效地构建了自调节加权偏差传递网络.

（2）提出改进半局部中心性算法WSLCA，对网络的关键节点进行识别，提出基于逆向回溯算法和重要度排名指标的关键节点的误差源识别方法.

（3）以具有代表性的锥齿轮轴组件的多阶段装配过程为研究对象，验证了所提方法的可行性和有效性，为复杂多阶段装配过程的质量监控和误差溯源提供了新的思路.

（4）在拥有数百个装配件的大规模装配过程形成的网络中，会形成以某关键节点为中心的簇，而误差的传递演化也主要是在该簇形成的社团中. 后续研究可以考虑将大规模的网络划分为不同的社团以简化关键节点的查找和误差溯源过程.