随着多种生命体全基因组序列的破译和功能基因组研究的开展,生物学家将关注点逐渐转移到对蛋白质组学的研究[1]. 蛋白质是一切生命的物质基础,是机体细胞的重要组成部分,是人体组织更新和修补的主要原料. 蛋白质并不是以个体为单位产生作用的,而是通过多种方式构成特定的蛋白质功能模块来完成特定的生命功能. 生物体内所有蛋白质的相互作用被称为蛋白质相互作用网络(protein-protein interaction network,PPIN)[2]. 从PPIN中挖掘蛋白质功能模块不仅能够为揭示蛋白质网络的组成结构、预测蛋白质功能、解释特定的生物进程提供实验基础和理论依据[3],而且能够在疾病预测、药物开发等方面发挥重要的作用[4].
为了检测生命体中的蛋白质功能模块,生物学家设计了许多生物实验方法. 近年来随着高通量生物技术的发展,海量的蛋白质相互作用数据不断涌现[5],生物实验方法由于检测周期长、开销大等局限性已无法满足时代发展的需求. 21世纪科技的进步带动了基于机器学习、数据挖掘等计算方法的迅速兴起,通过聚类算法高效识别PPIN中功能模块的方法逐渐发展起来[6]. Wu等[7]提出基于核心-附属关系的聚类方法(core-attachment based method,COACH),该方法首先检测出模块的核心蛋白质,然后将附属蛋白质逐个分派到核心蛋白质所在的模块中. Aldecoa等[8]提出的Jerarca算法基于层次聚类思想,计算蛋白质节点间的距离权重,利用距离权重构建层次结构树,然后根据模块内和模块间节点的连接分布进行层次划分得到功能模块. Nepusz等[9]设计了利用重叠邻域进行扩展的聚类方法(clustering with overlapping neighborhood expansion,ClusterONE),该算法能够检测潜在的重叠蛋白质功能模块,还可以识别一个功能模块完全被另一个功模块包含的情况. Liu等[10]基于显露模式(emerging patterns,EPs)方法提出有监督聚类算法ClusterEPs,该算法通过对比正负数据类发现真实模块的特征信息,定义基于EPs的聚类评分来识别当前未知的蛋白质功能模块. 近年来,群集智能算法已成功应用于PPIN功能模块检测领域. Ji等[11]基于蚁群寻优思想提出PPIN功能模块检测方法NACO-FMD,该方法融合了PPIN的拓扑信息和功能信息,并设计了有效的启发函数和一系列新的后处理策略来提高功能模块的检测质量. Ji等[12]设计了适合检测大规模PPIN的多粒度模型,此模型通过缩小PPIN的规模来缩短求解时间,并在消粒度过程中利用边界节点细化机制处理模块重叠问题. Yang等[13]提出基于细菌觅食机理的PPIN功能模块检测算法BFO-FMD,利用细菌觅食的4种生物行为设计了4种相应的有效进化机制. 由上可见,群智能算法已成为解决PPIN功能模块检测问题的有效手段.
为了提高功能模块的检测质量,探索更加高效的群智能算法,本研究模拟自然界中蝙蝠利用超声波捕食的行为,提出基于蝙蝠算法的PPIN功能模块检测方法(bat algorithm for functional module detection in PPIN,BA-FMD),通过调节声波脉冲频度协调每个蝙蝠个体的移动方向,将全局搜索和局部搜索相结合以增强算法的寻优能力和鲁棒性,期望得到更优的蛋白质网络功能模块划分.
1. 蝙蝠算法
蝙蝠是唯一能振翅飞翔的哺乳动物,大多数蝙蝠是食虫类动物. 蝙蝠是著名的“夜行侠”,虽然它的视力较差,但它却拥有超常的回声定位能力,可在黑暗中导航觅食. 蝙蝠在初始搜索猎物的过程中,发射的脉冲响度大而频度较低,随着自身与猎物距离的缩小,蝙蝠会增大脉冲发射频度并减小脉冲响度以便于精确定位猎物的空间位置[14]. Yang[15]将蝙蝠利用超声波捕食的行为与目标函数优化问题相联系,提出启发式随机搜索的蝙蝠算法(bat algorithm,BA). 该算法由于具有模型简单、易于实现、潜在的并行性和分布式等特点,被广泛用于工程优化[16-17]、聚类[18-19]、网络模型优化[20]、病理检测[21]、粒子滤波器优化[22]等领域.
蝙蝠算法有3个基本要素:脉冲频率
算法的具体步骤如下.
1)在目标函数优化问题中,设定义域为d维搜索空间,每个蝙蝠个体根据不同的脉冲频率来更新飞行速度和位置:
式中:
2)生成均匀分布随机数rand1,若
式中:
3)生成均匀分布随机数rand2,若
式中:α、γ为常数,分别为响度衰减系数和脉冲频度增强系数,
4)重复上述过程,直至满足某种收敛准则从而得到全局最优解和最优值.
蝙蝠算法的基本流程如算法1所示.
算法1:蝙蝠算法
输入:目标函数
输出:
初始化:
设置参数值:种群数量M、最大响度
随机初始化种群,确定每个个体的
根据
while (t < T)
1. for i=1 to M
2. 根据式(1)~(3)调整频率创建新解;
3. if
4. then 根据式(4)执行局部搜索;
5. else 根据式(5)执行全局搜索;
6. end if
7. 计算蝙蝠所处位置的
8. if
9. then接受新解并按照式(6)~(7)更新
10. end if
11. end for
12. 所有蝙蝠个体按照
13. t++;
end while
输出最优蝙蝠个体所在的位置
2. BA-FMD算法
BA-FMD算法利用蝙蝠算法的寻优机制完成PPIN功能模块检测. 1)在搜索空间中采用随机游走的方法初始化蝙蝠种群,每只蝙蝠所处位置代表一个候选功能模块划分,同时每个蝙蝠个体均被赋予较大的脉冲响度和较低的脉冲频度;2)在种群优化阶段,每个蝙蝠个体根据脉冲频度动态选择定向局部扰动操作或随机扰动操作,若移动后功能模块划分的效果有所改善,则接受更新之后的解并减小脉冲响度、增大脉冲频度;3)基于当前解与最优解之间的距离,以不同的脉冲频率执行自适应变异操作;4)根据自然界中优胜劣汰的进化机制执行自然选择操作,通过定向局部扰动、随机扰动、基于距离和频率的自适应变异、自然选择这4种机制的结合不断优化种群,从而得到最优或次优的功能模块划分;5)利用合并和过滤2个后处理操作对最优或次优的功能模块划分做进一步的修正.
2.1. 蝙蝠个体位置的编码及初始化
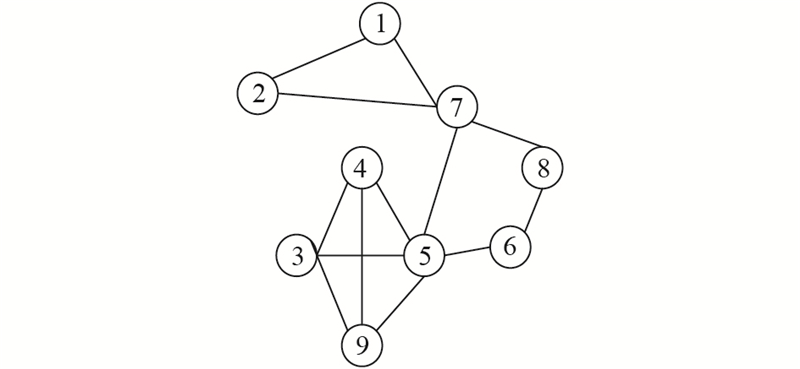
BA-FMD中每个蝙蝠个体的位置代表一种候选的功能模块划分,将其编码为有N个有向边的图,xi={(1→xi1), (2→xi2), ···, (k→xik), ···, (N→xiN)},其中,k为节点编号,xik为节点k的连接节点,N为PPIN中的节点总数. 采用随机游走的方式对蝙蝠个体位置进行初始化,具体步骤如下:
图 1
图 2
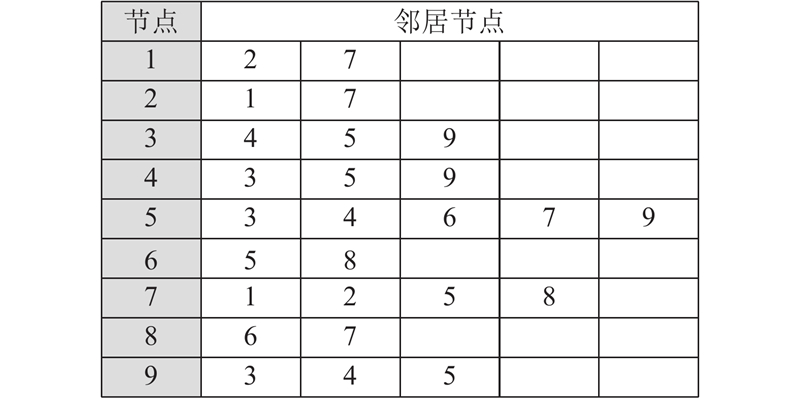
图 2 蝙蝠个体初始化时的邻居有序表
Fig.2 Ordered adjacency list in initialization of bat individual
图 3
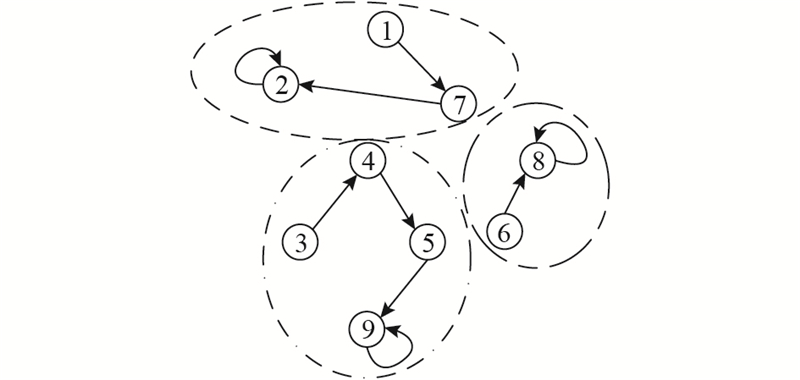
图 3 BA-FMD算法中蝙蝠个体的位置编码
Fig.3 Encoding of bat individual position in BA-FMD algorithm
3)对该蝙蝠个体位置进行解码得到一种功能模块划分,其中相连接的节点在同一个功能模块,不相连接的节点不在同一个模块,结果如图4所示.
图 4
图 4 BA-FMD算法中蝙蝠个体位置解码后的功能模块
Fig.4 Functional modules after decoding of bat individual position in BA-FMD algorithm
在蝙蝠个体i中,假设随机选中的节点为k,则k要连接l节点的概率为
式中:
式中:
2.2. 适应度函数的设置
在BA-FMD算法中,为了突出蛋白质功能模块簇内连接紧密而簇间连接稀疏的特点,将模块密度函数作为蝙蝠个体i的适应度:
式中:
2.3. BA-FMD的优化过程
BA-FMD的优化过程主要包括定向局部扰动操作、随机扰动操作、基于距离和频率的自适应变异操作、自然选择操作4种机制. 其中,定向局部扰动操作和随机扰动操作的选择是由每个个体的脉冲频度高低所决定的,拥有较低脉冲频度的个体执行定向局部扰动操作,否则执行随机扰动操作.
2.3.1. 定向局部扰动操作
若蝙蝠个体i的脉冲频度较低,说明它目前的进化过程并没有向着适应度增大的方向移动,且距离目标位置较远. 此时选择若干个较优蝙蝠,使蝙蝠个体i直接在较优蝙蝠附近产生新的位置,以快速提升蝙蝠个体i的适应能力. 将这种在较优解周围进行局部搜索的机制定义为定向局部扰动操作. 此策略的关键在于较优蝙蝠的选择数目. 在本研究中,较优蝙蝠数目的选择由该个体位置中每个节点与其连接节点之间的连接情况来决定. 在优化初期,蝙蝠种群分布较稀疏,脉冲频度也普遍较低,大多数个体中节点与其连接节点之间的相似度较差,此时在执行定向局部扰动操作时若选择较多的较优蝙蝠,有助于个体快速向较优解移动同时又保留了种群的多样性,并在一定程度上限制其陷入局部最优;在优化后期,随着所有个体基本都趋于较优的位置,且脉冲频度较高,大多数个体中节点与其连接节点之间的相似度较大,执行定向局部扰动操作的可能性大大降低,此时已没必要选择较多的较优蝙蝠,此时选择较少的较优蝙蝠,可以有效缩减计算量.
对于蝙蝠个体i的位置
式中:
定向局部扰动操作的具体步骤如下.
1)首先统计
2)将m个较优个体提取出来,对于每一个节点k,统计在m个较优个体中k节点的连接节点是l的个体数,将其占m的比值作为k节点要连接l节点的概率
式中:
3)在j和
算法2:BA-FMD中的定向局部扰动操作
输入:
参数:N,M,ε;
输出:定向局部扰动操作后蝙蝠个体i的新位置
由式(13)、(14)计算
for k=1 to N
1. 由m个蝙蝠计算k节点连接每个节点的概率式(15)、(16);
2. 根据概率利用轮盘赌机制得到k节点的最终连接节点j;
3. if(
4. else
5. end if
end for
输出
该操作的执行过程如图5所示. 图中,
图 5
图 5 BA-FMD算法中蝙蝠个体定向局部扰动操作示意图
Fig.5 Schematic diagram of directional local disturbance operation of bat individual in BA-FMD algorithm
2.3.2. 随机扰动操作
若蝙蝠个体i的脉冲频度较高,说明它之前的移动方向大体正确,目前也已经到达了相对较优越的位置,则只须在搜索空间随机扰动,观察是否能找到比当前状态更优的位置. 本研究将这种机制定义为随机扰动操作,其具体步骤如下:1)在
图 6
图 6 BA-FMD算法中蝙蝠个体随机扰动操作示意图
Fig.6 Schematic diagram of random disturbance operation of bat individual in BA-FMD algorithm
算法3:BA-FMD中的随机扰动操作
输入:
参数:N,p;
输出:随机扰动操作后蝙蝠个体i的新位置
1. 生成随机数
2. 生成N维向量
3. 对于
4. if(
5. else
6. end if
输出
2.3.3. 基于距离和频率的自适应变异操作
在种群中每个蝙蝠个体以不同的脉冲频率进行搜索,由式(2)可以看出,蝙蝠个体的飞行速度由脉冲频率和它与最优解之间的距离共同决定. 模拟此操作,将策略定义为基于距离和频率的自适应变异操作. 在每一代进化中,蝙蝠个体i与最优解的距离越大,说明该个体的进化空间越大,此时设置较大的自适应步伐有助于该个体向最优解快速迈进. 操作的具体步骤如下.
1)计算个体位置
式中:
2)在
具体流程如算法4所示.
算法4:基于距离和频率的自适应变异操作
输入:
参数:N,
输出:基于距离和频率的自适应变异操作后蝙蝠个体i的新位置
1. 由式(17)、(18)计算个体i与当前最优解的距离;
2. 设置个体i的频率
3. if(
4. then 重新初始化得到
5. else 生成N维向量
对于
6. if(
7. then
8. else
9. end if
10. end if
输出
2.3.4. 自然选择操作
将种群中的个体按照适应度进行排序,根据生物界的优胜劣汰规律,淘汰种群中η个较差个体,并将η个较优个体进行复制放入种群,这样不仅保证了种群规模,同时还提升了种群的适应能力. 将此策略定义为自然选择操作,其中η的表达式为
式中:t为目前迭代次数,η随着进化的深入而不断变小. 通常,种群在进化的前期具有较好的多样性,但是随机性较强,较大的淘汰数量可以迅速提升种群整体的适应性;在进化的后期,算法逐渐收敛,减小淘汰数量可以保留种群的多样性.
2.4. 算法描述与分析
1)BA-FMD算法首先产生一个初始种群,种群中每个蝙蝠个体以较大的脉冲响度和较低的脉冲频度进行搜索,每只蝙蝠所处位置编码为一个候选功能模块划分. 2)在种群优化阶段,发射较低脉冲频度的蝙蝠执行定向局部扰动操作,即在选择的较好解周围进行局部搜索;发射较高脉冲频度的蝙蝠执行随机扰动操作,在搜索空间寻找更优的解;若更新之后所有功能模块的模块密度增大,则接受新解并减小脉冲响度、增大脉冲频度;3)采用基于距离和频率的自适应变异操作对候选解进行优化,根据当前解与最优解之间的距离设置向最优解迈进的自适应步伐,并以一定的可能性将该个体重新初始化为一个功能模块划分,从而有效避免种群陷入局部最优;4)对整个种群执行自然选择操作提升种群整体的适应能力,加快算法的收敛速度. 通过这4种机制的结合不断优化种群,得到最优或次优的功能模块划分. 最后利用合并和过滤2个后处理操作对最优或次优的功能模块划分做进一步的修正. BA-FMD算法的具体流程如算法5所示. 其中,G (V, E)中,G为PPIN,V为G中所有节点的集合,E为G中所有边的集合.
算法5:BA-FMD
输入:PPIN:G(V,E),N=|V|;GO信息;
输出:PPIN功能模块集合;
初始化:
设置参数值:M、最优解保持不变的最大迭代次数Q、p、
计算每2个节点的相似度;
初始化种群:
for i=1 to M
选择任意蛋白质节点kϵ[1,N],根据式(8)选择l作为k的连接节点,再将l节点作为起始节点确定其连接节点,直到所有的节点被遍历,形成个体i的模块划分
end for
蝙蝠算法优化种群:
计算每个蝙蝠个体的适应度
最优个体适应度为
迭代次数t=1;由式(6)、(7)计算
最优个体适应度不变的迭代次数q=0;
while q<Q
1. for i=1 to M
2. if
3. then执行定向局部扰动操作;
4. else执行随机扰动操作;
5. end if
6. if
7. then接受新解,按照式(6)、(7)更新
8. end if
9. end for
10. 计算每个蝙蝠个体的适应度并排序,更新最优解;
11. for i=1 to M
12. 执行基于距离和频率的自适应变异操作;
13. end for
14. 执行自然选择操作;
15. if (
16. else q=0;
17. end if
18. t++;
end while
对优化得到的最好解进行合并和过滤2个后处理操作[11];
输出后处理之后的PPIN功能模块划分.
基于算法5的描述,对BA-FMD的时间复杂度进行分析. 在初始化过程中,计算每2个节点相似度的时间复杂度为
3. 实验结果与分析
本实验在处理器为Core(TM)i5-6500 CPU、RAM为4.00 GB、操作系统为Windows10的环境下,利用eclipse运行工具编写Java代码进行实现.
3.1. PPIN数据集
表 1 Gavin、DIPcore、Krogan、Collins、BioGRID数据集的节点与边数目
Tab.1
| 数据集 | 节点数目 | 边数目 |
| Gavin | 1 430 | 6 531 |
| DIPcore | 2 508 | 5 673 |
| Krogan | 3 672 | 14 317 |
| Collins | 1 622 | 9 074 |
| BioGRID | 5 640 | 59 748 |
3.2. 评价指标
采用3组常见的评价指标来证明算法的有效性.
3.2.1. 覆盖率
在检测功能模块的过程中,有可能将一些蛋白质节点丢弃或者过滤. 覆盖率(coverage)指标为检测的所有功能模块组成的蛋白质节点集合中元素个数占蛋白质节点总数的比例,表达式为
式中:
3.2.2. 精度、召回率和F度量
精度(precision)、召回率(recall)和F度量(F-measure)是检测PPIN功能模块问题中常用的评价指标. 在计算这些评价指标之前首先要计算邻域亲和评分(neighborhood affinity,NA),此评分衡量检测模块
若
式中:Pr为精度,Rc为召回率,
F度量是精度和召回率的调和平均值,表达式为
3.2.3. 灵敏度、正的预测率和准确度
灵敏度Sn(sensitivity)、正的预测率PPV(positive predictive value)和准确度Acc(accuracy)是另一组评价功能模块检测方法的指标. 表达式分别为
式中:
3.3. 实验分析与比较
对于不同的PPIN数据集,以Cv、Pr、Rc、Fm、Sn、PPV、Acc作为评价指标,通过控制变量法对每一个数据集的参数进行多次调试,从而确定每个数据集的参数. 5个数据集共有的参数确定为:M=100、p=0.62、α=γ=0.95、
表 2 BA-FMD算法在不同数据集上的连接相似度阈值和过滤阈值
Tab.2
| 数据集 | ε | δ |
| Gavin | 0.24 | 0.04 |
| DIPcore | 0.36 | 0.04 |
| Krogan | 0.30 | 0.04 |
| Collins | 0.36 | 0.04 |
| BioGRID | 0.24 | 0.18 |
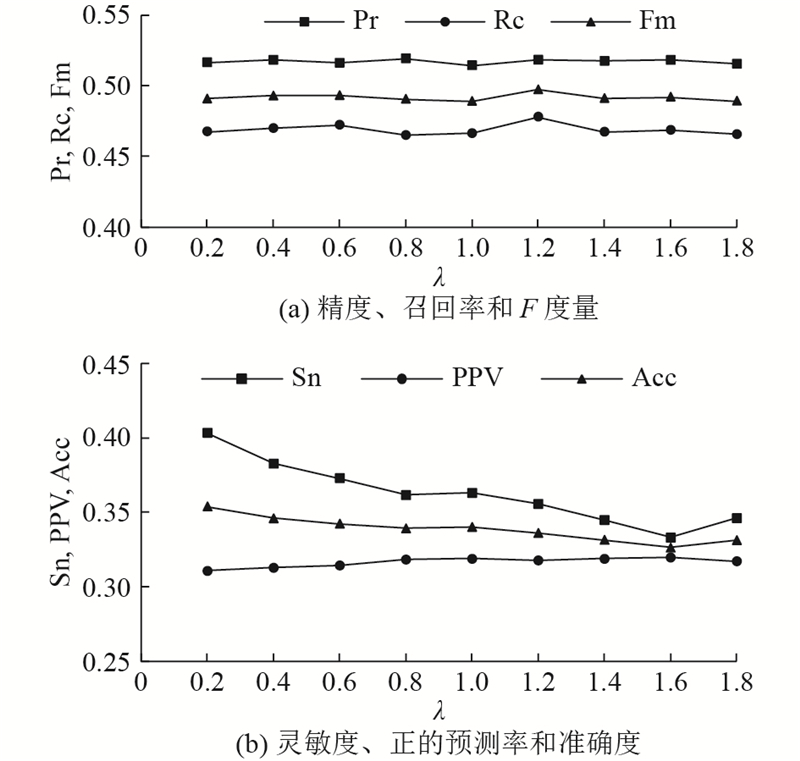
对所有参数取值方法进行详细描述. 对于M、p、
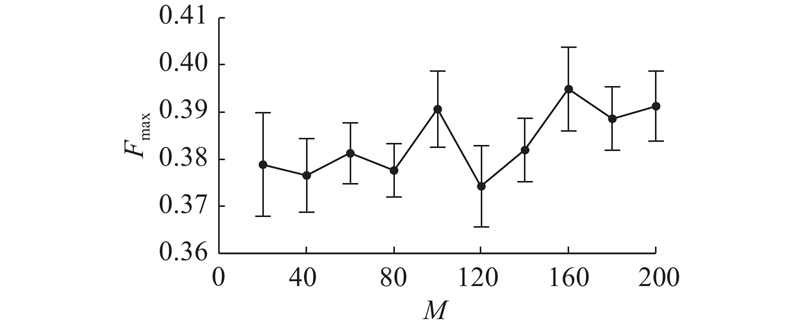
图 7
图 7 BA-FMD算法在不同种群规模下达到收敛时的最优个体适应度
Fig.7 Optimal individual fitness of BA-FMD algorithm for convergence under different population sizes
图 8
图 8 BA-FMD算法在不同合并阈值下评价指标的取值
Fig.8 Values of evaluation indexes under different combined thresholds in BA-FMD algorithm
将每个数据集在以上相应参数下独立运行15次取平均值作为最终的实验结果. 为了验证BA-FMD算法的有效性,将其与NACO-FMD、BFO-FMD、Jerarca、COACH、ClusterONE、ClusterEPs这6个经典算法进行对比. 7种算法在5个不同规模数据集上的基本检测结果如表3所示,其中包括检测模块数、检测模块平均大小、
表 3 7种算法在5个数据集上的实验结果
Tab.3
| 算法 | 数据集 | 结果 | |||
| 模块数 | 模块平均大小 | Na≥0.2 | Nb≥0.2 | ||
| BA-FMD | Gavin | 215 | 6.48 | 111 | 198 |
| DIPcore | 416 | 6.01 | 163 | 252 | |
| Krogan | 521 | 6.93 | 135 | 190 | |
| Collins | 291 | 5.45 | 148 | 244 | |
| BioGRID | 731 | 6.02 | 218 | 295 | |
| NACO-FMD | Gavin | 115 | 7.31 | 80 | 163 |
| DIPcore | 311 | 5.00 | 125 | 209 | |
| Krogan | 183 | 2.81 | 77 | 115 | |
| Collins | 254 | 3.58 | 129 | 162 | |
| BioGRID | 195 | 3.21 | 72 | 92 | |
| BFO-FMD | Gavin | 146 | 6.57 | 94 | 176 |
| DIPcore | 302 | 6.29 | 153 | 246 | |
| Krogan | 189 | 7.04 | 80 | 145 | |
| Collins | 268 | 5.63 | 148 | 252 | |
| BioGRID | 281 | 5.73 | 140 | 220 | |
| Jerarca | Gavin | 259 | 5.39 | 99 | 174 |
| DIPcore | 583 | 4.34 | 151 | 230 | |
| Krogan | 727 | 4.05 | 101 | 167 | |
| Collins | 385 | 4.21 | 150 | 245 | |
| BioGRID | 1 313 | 4.30 | 98 | 156 | |
| COACH | Gavin | 324 | 2.34 | 122 | 197 |
| DIPcore | 381 | 2.87 | 136 | 155 | |
| Krogan | 579 | 9.29 | 247 | 190 | |
| Collins | 251 | 18.02 | 176 | 199 | |
| BioGRID | 1 507 | 22.85 | 410 | 264 | |
| ClusterONE | Gavin | 243 | 5.92 | 102 | 156 |
| DIPcore | 269 | 4.13 | 115 | 157 | |
| Krogan | 240 | 4.68 | 100 | 139 | |
| Collins | 203 | 6.44 | 118 | 201 | |
| BioGRID | 475 | 6.56 | 163 | 219 | |
| ClusterEPs | Gavin | 297 | 5.03 | 171 | 165 |
| DIPcore | 354 | 4.72 | 208 | 182 | |
| Krogan | 494 | 6.62 | 297 | 178 | |
| Collins | 173 | 9.82 | 132 | 170 | |
| BioGRID | 822 | 5.50 | 396 | 252 | |
以DIPcore数据集为例,简单介绍表格的含义,在DIPcore数据集上,BA-FMD算法检测到的功能模块数为416个,其中有163个检测模块与252个标准功能模块相匹配,检测到的功能模块平均包含6个蛋白质. 可以看出,在5个数据集中,BA-FMD算法在
为了进一步证明BA-FMD算法的优越性,如图9所示为7种算法在5个数据集上的7个不同评价指标的对比结果. 综合5个子图的结果可以看出,BA-FMD算法在Gavin、Krogan、Collins、BioGRID这4个数据集上均有4项指标排名第一,在DIPcore数据集上有3项指标排名第一,其余指标也大多排名前三.
图 9
图 9 7种算法在5个数据集上的不同评价指标比较
Fig.9 Comparison of different evaluation indexes of seven algorithms on five datasets
1)对于Acc综合指标,BA-FMD算法在5个数据集上均取得了最好的结果. 2)BA-FMD算法在Cv指标上也占有绝对优势,在5个数据集中比排名第二的算法分别高出13.0%、23.0%、12.0%、5.0%、0.5%,说明BA-FMD算法在聚类过程中丢弃的蛋白质较少,能够将大多数蛋白质划分到功能模块中,从而有可能探测到几乎每个蛋白质在生命过程中的功能. 3)BA-FMD算法在Rc指标上表现出色,在Gavin、DIPcore、Krogan、BioGRID这4个数据集中都取得了第一的成绩;在Collins数据集中虽排名第三,但与第一、第二的BFO-FMD、Jerarca较接近. 4)BA-FMD算法在Sn指标上也表现较好,在Gavin、Krogan、Collins 这3个数据集中排名第一;在DIPcore数据集中排名第二,与排名第一的BFO-FMD表现基本齐平;在BioGRID大型数据集中与同类算法BFO-FMD、NACO-FMD相比有明显优势,但不如Jerarca和COACH的表现,这是因为本研究的初始化方法无法识别重叠的功能模块,致使功能模块分布较均匀,而Jerarca和COACH在BioGRID中识别出多个较大的功能模块,与标准模块共有蛋白质的数量较多,Sn指标较高. 5)BA-FMD算法在PPV上表现也不差,在Collins和BioGRID数据集中均取得了最好的结果;在Gavin、DIPcore、Krogan数据集中均略逊于NACO-FMD排名第二,说明PPIN所蕴含的网络特性不同,即使采用同类算法,由于优化机理不同,算法的检测性能也会有所不同.
综合以上5个指标,BA-FMD算法均取得了不错的结果. 原因如下:1)本研究利用动态变化的脉冲频度调节蝙蝠个体的移动方向,使每个蝙蝠个体根据自己当前移动方向情况智能变换下一步的移动策略;2)其次,基于距离和频率的自适应变异操作通过与最优个体位置距离的比较来决定自身位置变化的程度,同时,以一定的可能性重新初始化某些个体,也为种群注入了新鲜血液;3)依据生物界中优胜劣汰的生存法则设计的自然选择操作,大大加快了种群进化的速度,提升了种群的适应能力,使算法获得更优秀的解.
不过,BA-FMD算法在Pr指标上表现不佳,造成该现象的主要原因是BA-FMD算法舍弃的蛋白质节点较少,而在该指标上表现较好的算法大多舍弃了大量的蛋白质,在Pr指标上的表现与Cv指标完全相反. 值得一提的是,结合Pr指标和Rc指标,BA-FMD在4个数据集上均得到了具有竞争力的综合指标Fm,具体来说,该指标在Gavin数据集上以稍低于BFO-FMD算法的结果排名第二;在DIPcore、Collins、BioGRID数据集上排名第三;在Krogan数据集上因Pr指标表现不佳,Fm指标效果也不佳.
通过以上分析可知,BA-FMD算法与其他6种算法相比,在5个不同规模的PPIN数据集上均取得了较好的检测结果,表明BA-FMD算法是有效的功能模块检测方法.
4. 结 语
基于蝙蝠觅食原理设计了PPIN功能模块检测的新方法BA-FMD. 该算法最主要的特点是利用标准蝙蝠算法的基本思想,提出了定向局部扰动操作、随机扰动操作、基于距离和频率的自适应变异操作,利用这些优化机制对搜索空间中每一个功能模块划分进行优化;此外,采用较好个体替代较差个体的自然选择操作来提升整个种群的功能模块划分效果. 在5个数据集上进行的实验充分表明BA-FMD算法是有效的检测PPIN功能模块的方法. 该方法的研究,不仅拓展了蝙蝠算法的应用领域,而且对其他复杂网络的分析与研究也有一定的借鉴意义. 本研究所提出的算法未识别出重叠模块,在未来的工作中,将充分考虑重叠模块的检测问题,并融合更多生物信息,获得更高的检测质量,将高质量的功能模块应用到具体的疾病预测中.
参考文献
Tissue-based map of the human proteome
[J].DOI:10.1126/science.1260419 [本文引用: 1]
HIV-1, human interaction database: current status and new features
[J].DOI:10.1093/nar/gku1126 [本文引用: 1]
A novel method to predict protein complexes based on Gene Ontology in PPI networks
[J].
Survey: functional module detection from protein-protein interaction networks
[J].DOI:10.1109/TKDE.2012.225 [本文引用: 1]
动态蛋白质网络的构建、分析及应用研究进展
[J].DOI:10.7544/issn1000-1239.2017.20160902 [本文引用: 1]
The construction, analysis, and applications of dynamic protein-protein interaction networks
[J].DOI:10.7544/issn1000-1239.2017.20160902 [本文引用: 1]
蛋白质相互作用网络功能模块检测的研究综述
[J].
An overview of research on functional module detection for protein-protein interaction networks
[J].
A core-attachment based method to detect protein complexes in PPI networks
[J].DOI:10.1186/1471-2105-10-169 [本文引用: 1]
Jerarca: efficient analysis of complex networks using hierarchical clustering
[J].DOI:10.1371/journal.pone.0011585 [本文引用: 1]
Detecting overlapping protein complexes in protein-protein interaction networks
[J].DOI:10.1038/nmeth.1938 [本文引用: 1]
Using contrast patterns between true complexes and random subgraphs in PPI networks to predict unknown protein complexes
[J].DOI:10.1038/srep21223 [本文引用: 1]
Detecting functional modules based on a multiple-grain model in large-scale protein-protein interaction networks
[J].
BFO-FMD: bacterial foraging optimization for functional module detection in protein-protein interaction networks
[J].DOI:10.1007/s00500-017-2584-9 [本文引用: 1]
回声定位蝙蝠及其声通讯
[J].DOI:10.3969/j.issn.0250-3263.2002.06.021 [本文引用: 1]
Echolocation and acoustic communication in bats
[J].DOI:10.3969/j.issn.0250-3263.2002.06.021 [本文引用: 1]
A new metaheuristic bat-inspired algorithm
[J].
The bat algorithm, variants and some practical engineering applications: a review
[J].
Multi-objective optimization using bat algorithm for shell and tube heat exchangers
[J].DOI:10.1016/j.applthermaleng.2016.09.031 [本文引用: 1]
MBA-LF: a new data clustering method using modified bat algorithm and levy flight
[J].
Multi-population cooperative bat algorithm-based optimization of artificial neural network model
[J].DOI:10.1016/j.ins.2014.08.050 [本文引用: 1]
A pathological brain detection system based on extreme learning machine optimized by bat algorithm
[J].DOI:10.2174/1871527315666161019153259 [本文引用: 1]
Dynamic perceptive bat algorithm used to optimize particle filter for tracking multiple targets
[J].DOI:10.1061/(ASCE)AS.1943-5525.0000834 [本文引用: 1]
Bootstrapping the interactome: unsupervised identification of protein complexes in yeast
[J].DOI:10.1089/cmb.2009.0023 [本文引用: 1]