目前关于网络增边的研究已取得一定的成果. Ghosh等[10]提出基于贪婪策略的加边方法,网络拓扑图的第二大拉普拉斯特征值反映了网络鲁棒性的强弱,以最大化第二大拉普拉斯特征值作为目标函数,每次加边都选择能使特征值最大的边. Kim[11]考虑拉普拉斯矩阵的第二小特征值,设计了基于二分法的网络加边策略,相较文献[10]中的贪婪策略,二分法更加简洁高效. Chen等[12]提出分别基于度中心性、接近中心性、介数中心性和特征向量中心性的加边策略,以应对网络攻击. Jiang等[13]分别采用随机加边、低度数加边和低介数加边的方法对网络拓扑结构进行改变,增强网络性能. Cao等[14]研究3种网络加边策略,分别为随机加边策略、高介数连边策略和低极化连边策略,并且考虑网络连接的成本问题. Shi等[15]提出保护关键节点的策略,在网络的关键节点之间增加冗余边,提高无标度网络的鲁棒性. Zhuo等[16]提出增强无标度网络鲁棒性的增边修复模型,并且提出新的边缘信息保护策略,可以降低增边的成本。Zhao等[17]提出被称为随机局部重新连边的网络重新连边方法,在增边时采用随机增边方法. 此外,部分研究着眼于提升网络的抗毁性[18-20],以应对网络可能遭受的攻击,即在战前的准备阶段,规划出鲁棒性较强的通信网络,但这种网络更多的是针对特定攻击方式而建立的,在遭遇其他攻击方式时,抗毁性会受到较大的影响.
结合当前的研究现状,本研究在节点不具有可恢复性的情况下,开展C2组织中军事通信网络的修复问题研究. 在目前的增边方法中,很多方法未考虑到连边的成本,或者是把边的总条数作为成本,具有一定的局限性. 本研究建立基于增边修复的网络修复模型,考虑网络的连接成本;提出求解模型的算法;通过不同的攻击策略以及与现有增边方法的对比,验证本研究所提出算法的有效性.
1. C2组织的通信网络
1.1. C2组织的基本实体
实体是C2组织的组成元素,组织内共有4类基本实体[21],分别为任务、平台、决策和通信实体. 下面对这4类实体进行详细描述.
1)任务实体. 任务实体T为作战使命分解后得到的军事行动,是组织为实现作战目标而采取的行动. 任务的执行须调用一个或多个平台实体. C2组织的任务集
2)平台实体. 平台实体P拥有作战资源,为C2组织中直接处理作战任务的实体,如无人机编队,炮兵连等. C2组织的平台集
3)决策实体. 决策实体DM为C2组织内的决策单元,是组织内进行指挥控制活动的承担者,如各级指挥机构. 组织内有1个战役决策实体(operational decision-maker, ODM)记为
4)通信实体. 通信实体为C2组织通信网络中的节点,包括卫星、地面中继站等. C2组织的通信实体集记为
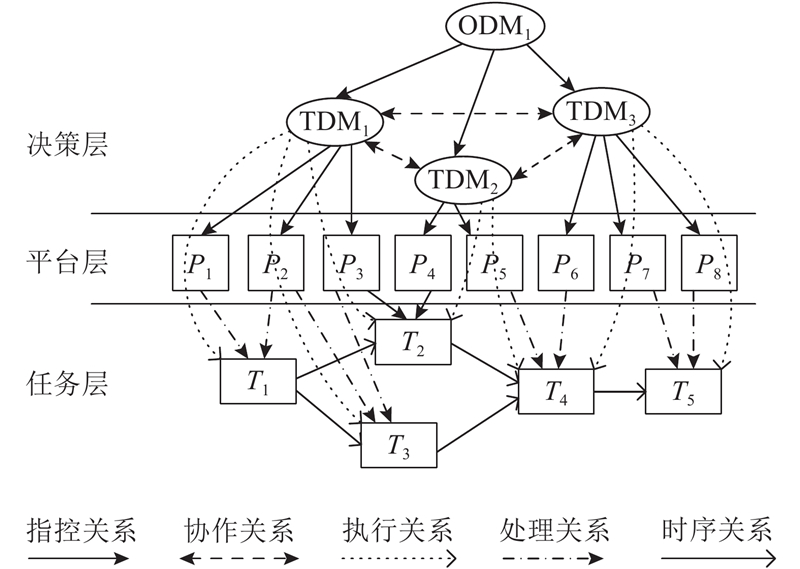
在以上4类实体中,任务实体、平台实体和决策实体这三者通过之间的相互关系(指控、协作、执行、处理等关系)形成C2组织的结构,如图1所示.
图 1
1.2. 通信结构
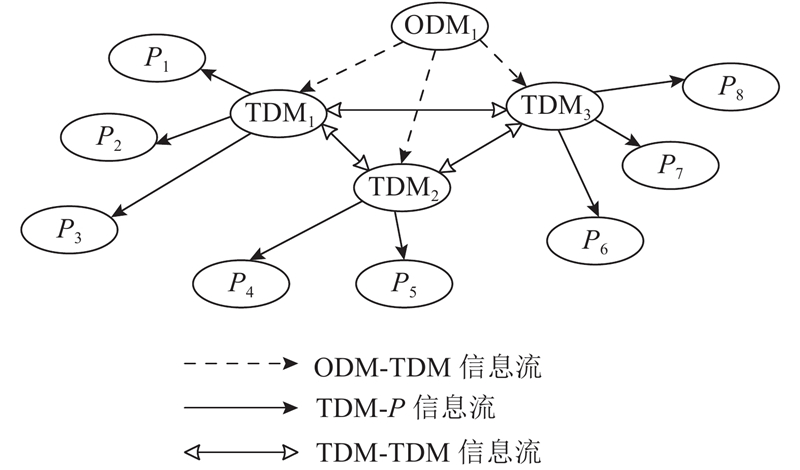
C2组织的军事通信网络是为保障组织中战役决策实体与战术决策实体(ODM-TDM)、战术决策实体与平台实体(TDM-P)、战术决策实体(TDM-TDM)之间的信息交互而规划的通信网络拓扑结构. 通信网络保障的3种信息流如图2所示. 通信实体之间的连接关系,即网络中通信节点的连接关系由
图 2
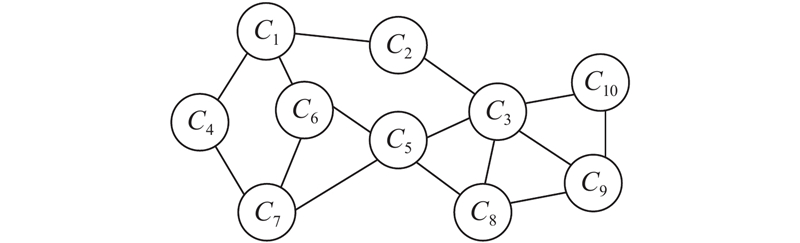
图 3
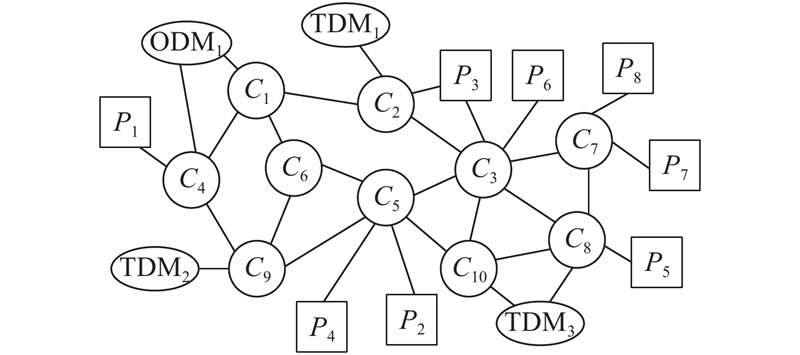
图 4
2. C2组织的通信网络的修复模型
在作战进程中受损的节点往往无法及时修复,因此,当某一节点损毁后,与此节点相连的边也无法连通. 针对这种情况,采用增边补偿的方法,在剩余的功能完整的节点之间增加边,以使网络能够连通.
2.1. 符号说明
通信结构所保障的ODM与TDM之间、TDM与平台之间、TDM之间的信息流,以及与这3种信息流相关的关系定义如下.
1)ODM与TDM之间的指挥控制关系.
2)TDM与平台实体之间的指挥控制关系.
3)TDM之间的协作关系.
4)ODM与TDM之间的连通关系.
5)TDM与平台实体之间的连通关系.
6)TDM之间的连通关系.
2.2. 目标函数
2.2.1. 网络对信息流的保障能力
网络对于每种信息流的保障能力由通信网络实际能够保障的信息流条数与须保障的信息流条数的比值来衡量:
式中:
2.2.2. 信息流传输时的抗毁度
在网络受到攻击时,网络中正常传递信息的信息流条数会随着通信实体的不断损毁而减少,因此网络在信息流传输时的抗毁度表达式为
式中:
2.2.3. 网络的抗毁度
在通信网络遭受到攻击时,若网络拓扑结构自身有较强的抗毁性,未受损的通信实体之间可以保持连通,则当C2组织的结构或者用户的接入发生改变后,组织中的业务信息流能较为顺利地传输. 因此,网络拓扑自身的抗毁性越高,保持自身连通的能力
式中:
综上,网络的综合抗毁度表达式为
式中:
将综合抗毁度作为网络受损后进行增边修复的目标函数,以得到最优抗毁度的连接方案作为修复目标.
2.3. 约束条件
在受到攻击后,依然有效的通信实体的集合为
1)增边约束. 增边修复的策略是在未建立连接的通信实体之间进行连边. 原有已建立连接的不做调整. 由新增的边构成的矩阵
2)连通约束. 修复后的通信网络中任意2个通信实体之间均连通,
3)成本约束. 在对网络进行修复时,须考虑到网络的连接成本. 考虑到在实际的通信网络中,节点之间的连接成本并不是由节点的度和介数所决定的[22],因而采用网络的边的连接程度来表征网络的连接成本,表达式为
式中:
由于网络中存在冗余边和必须边,冗余边的连接成本高于必须边,因此
式中:
当网络处于全连通状态时,网络的连接成本表达式为
式中:
无论是初始网络拓扑结构的构建还是受损网络的修复,考虑到成本问题,都不会采用成本最高的全连通网络,因此,定义成本的上限为
2.4. 修复模型
综上所述,通信网络增边修复的构造模型为
式中:
3. 基于离散人工蜂群算法的求解方法
3.1. 人工蜂群算法的基本原理
3.2. 算法相关步骤设计
结合本研究要求解的网络修复模型和离散人工蜂群算法的基本原理,对求解式(8)的关键步骤进行设计.
3.2.1. 编解码方法
将须优化的邻接矩阵
如表1所示,采用双串编码的方式. 在表1的第1行中记录
表 1 双串编码结构
Tab.1
| 序号 | YN(1) | YN(2) | ··· | YN(n) | ··· | YN(Z) |
| 0−1值 | x1 | x2 | ··· | xn | ··· | xZ |
3.2.2. 种群初始化
随机生成SN个满足初始条件的解,解的集合记为
式(9)的含义为:生成一个
3.2.3. 适应度函数
每个
3.2.4. 搜索过程
在每一轮迭代中,首先按照
3.2.5. 邻域搜索
与当前Z维解
式中:NRAND为以一定概率从邻域
3.2.6. 侦察蜂策略
在对同一个解进行Tlimit次邻域搜索之后,若该解的适应度仍未提高,就要使用侦察蜂策略,生成一个新解来替换此解,以促进算法跳出局优. 采用的离散优化问题的侦察蜂生成策略表达式为
式中:
3.3. 求解算法步骤
综上,采用离散人工蜂群算法求解网络修复模型的基本步骤如下:1)种群初始化,设置各项参数,按式(9)随机生成SN个初始解;2)按式(10)、(4)计算解集
4. 实验结果及分析
在复杂网络中,针对节点的攻击策略主要有2种类型,分别是随机攻击和故意攻击. 随机攻击,即随机地对网络中节点进行破坏;故意攻击,是按照节点连接度从大到小的顺序攻击节点. 本研究选择这2种攻击方式对所提出的网络连边修复算法进行验证[7].
表 2 战术决策实体对平台的指挥控制情况
Tab.2
| 战术决策实体 | 所指控的平台 |
| | |
| | |
| | |
| | |
表 3 决策实体与通信实体的连接关系
Tab.3
| 决策实体 | 所连接的通信实体 | 决策实体 | 所连接的通信实体 | |
| | | | | |
| | | | | |
| | |
表 4 平台实体与通信实体的连接关系
Tab.4
| 平台实体 | 所连接的通信实体 | 平台实体 | 所连接的通信实体 | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | |
图 5
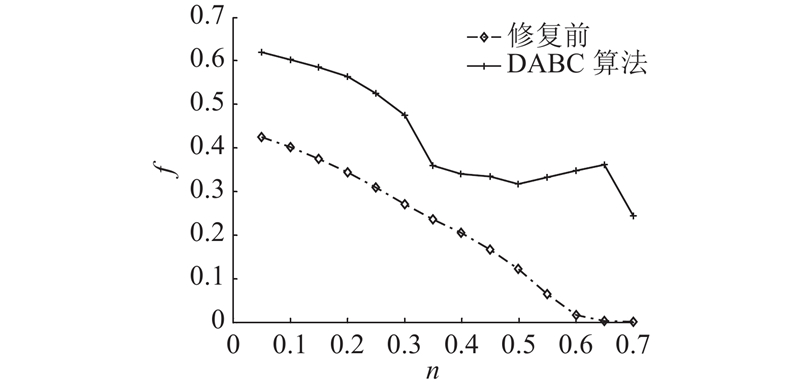
1)仿真实验1:方法可行性验证. 对通信网络分别进行随机攻击和故意攻击,在每种攻击方式下,设置不同的节点失效比例,对本研究的算法进行验证. 节点的损毁比例依次为0.05、0.10、0.15、0.20、0.25、0.30、0.35、0.40、0.45、0.50、0.55、0.60、0.65、0.70,蜂群规模SN设为200,最大停留次数Tlimit设为10,最大迭代次数
图 6
图 7
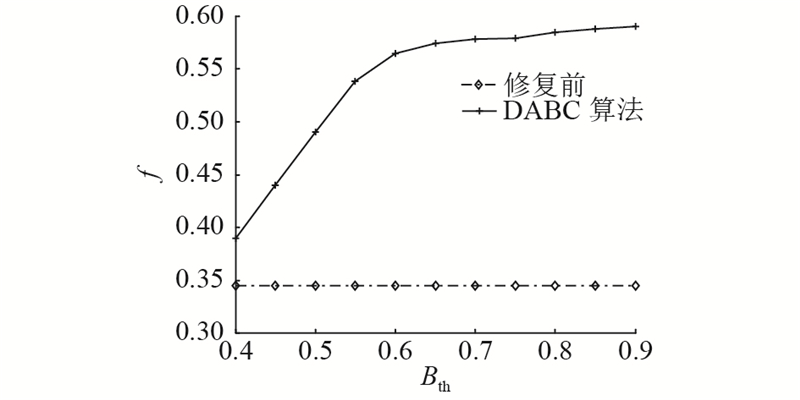
2)仿真实验2:连接成本分析. 网络的连接成本上限
图 8
图 8 随机攻击下的实验结果随成本的变化
Fig.8 Variation of experimental results with cost under random attack
图 9
图 9 故意攻击下的实验结果随成本的变化
Fig.9 Variation of experimental results with cost under deliberate attack
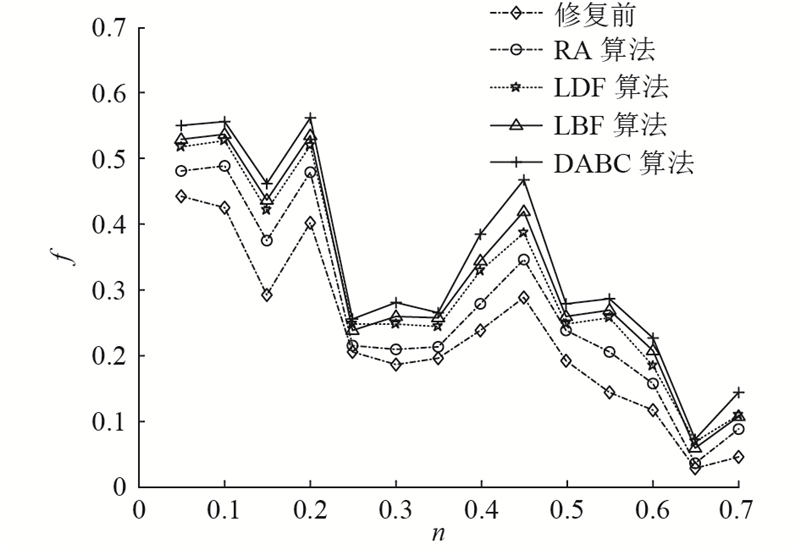
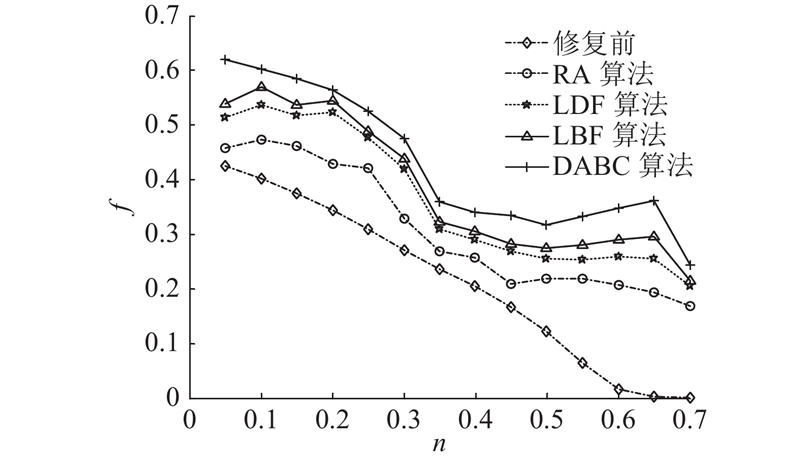
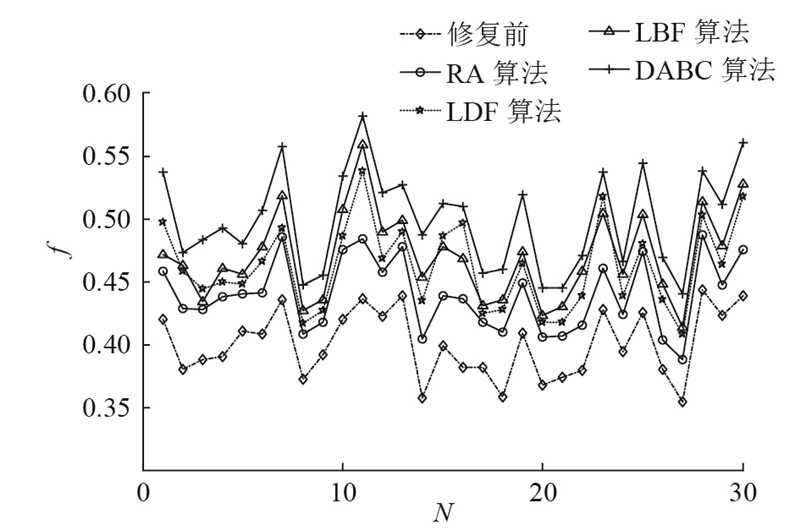
3)仿真实验3:算法性能比较. 将所提出的基于离散人工蜂群算法的模型求解算法同随机加边(random addition,RA)、低度数加边(low degree first,LDF)和低介数加边(low betweenness first,LBF)算法[13]进行对比.
a)随机加边算法,每次加边均是在网络中随机选择2个节点建立连接. 当网络的连接成本高于
b)低度数加边算法,每次加边均选择网络中度数最低的2个节点建立连接;当出现多个最低度数节点时,则在这些节点中随机选择2个节点进行连接. 当网络的连接成本高于
c)低介数加边算法,每次加边均选择网络中介数最低的2个节点建立连接;当出现多个最低介数节点时,则在这些节点中随机选择2个节点进行连接. 当网络的连接成本高于
图 10
图 13
图 13 故意攻击下不同算法的实验结果随成本上限的变化
Fig.13 Variation of experimental results with cost upper under deliberate attack for different algorithms
图 11
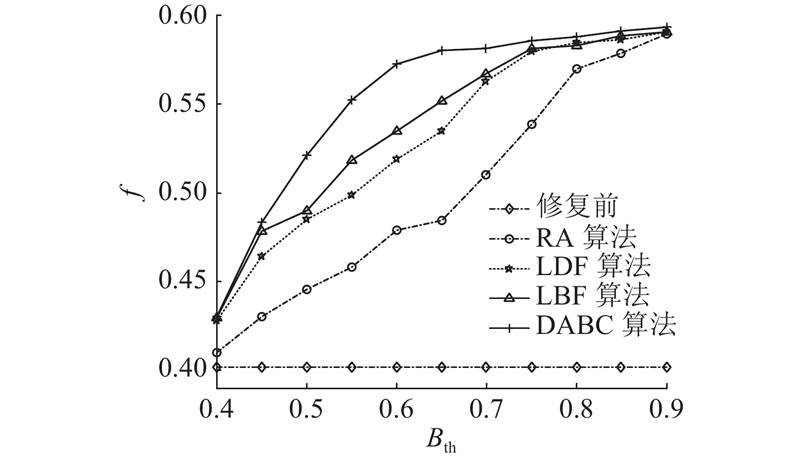
图 11 随机攻击下不同算法的实验结果随成本上限的变化
Fig.11 Variation of experimental results with cost upper under random attack for different algorithms
图 12
图 12 故意攻击下的算法性能的对比
Fig.12 Algorithm performance comparison under deliberate attack
图 14
图 14 随机攻击下不同权重系数的算法性能对比
Fig.14 Algorithm performance comparison of different weight coefficients under random attack
图 15
图 15 故意攻击下不同权重系数的算法性能对比
Fig.15 Algorithm performance comparison of different weight coefficients under deliberate attack
5. 结 语
针对C2组织中军事通信网络受到攻击后的网络拓扑修复问题进行研究,提出以高抗毁性为目标函数的受损网络增边修复模型;设计基于离散人工蜂群算法的模型求解方法;在随机攻击和选择性攻击2种条件下进行仿真验证,仿真结果表明本研究所设计方法可以有效地对受损的军事通信网络进行修复,以保障信息流的正常传输. 所采用的增边策略属于随机优化选取的方式,对于网络的特性分析较少,在初始增边时存在一定的盲目性. 在下一步研究中,考虑将网络的特性与优化算法相结合来进行增边操作.
参考文献
Quantifying the impact of information and organizational structures via distributed auction algorithm: point-to-point communication structure
[J].DOI:10.1109/TSMCA.2011.2157139
Network centric military communications
[J].
Stability of random networks under evolution of attack and repair
[J].DOI:10.1088/0256-307X/23/1/076 [本文引用: 2]
基于拓扑信息的网络修复
[J].DOI:10.3778/j.issn.1002-8331.2008.05.007 [本文引用: 1]
Network restoration based on topological information
[J].DOI:10.3778/j.issn.1002-8331.2008.05.007 [本文引用: 1]
多种攻击策略下无标度网络修复策略
[J].
Repair strategies of scale-free networks under multifold attack strategies
[J].
多属性加权模糊贝叶斯的复杂网络故障自修复技术
[J].DOI:10.3969/j.issn.1001-3695.2015.08.033
Complex network fault self-repair mechanism with multi-attribute weighted fuzzy Bayesian
[J].DOI:10.3969/j.issn.1001-3695.2015.08.033
修复策略下典型拓扑结构复杂网络抗毁性研究
[J].
Invulnerability analysis of complex networks with typical topologies by repair strategies
[J].
Bisection algorithm of increasing algebraic connectivity by adding an edge
[J].DOI:10.1109/TAC.2009.2033763 [本文引用: 1]
Assessing and safeguarding network resilience to nodal attacks
[J].DOI:10.1109/MCOM.2014.6957154 [本文引用: 1]
Enhancing network performance by edge addition
[J].DOI:10.1142/S0129183111016841 [本文引用: 2]
Improving the network robustness against cascading failures by adding links
[J].
A new way to improve the robustness of complex communication networks by allocating redundancy links
[J].DOI:10.1088/0031-8949/85/03/035803 [本文引用: 1]
Improving the attack tolerance of scale-free networks by adding and hiding edges
[J].DOI:10.1088/0031-8949/83/02/025801 [本文引用: 1]
Achieving high robustness in supply distribution networks by rewiring
[J].DOI:10.1109/TEM.2010.2095503 [本文引用: 1]
Optimal attack strategy of complex networks based on tabu search
[J].DOI:10.1016/j.physa.2015.08.043 [本文引用: 1]
复杂网络抗毁性研究进展
[J].DOI:10.3969/j.issn.1007-6735.2011.06.022
Progress in invulnerability of complex networks
[J].DOI:10.3969/j.issn.1007-6735.2011.06.022
军事通信网抗毁性研究
[J].
Survivability studies for military communication network
[J].
Normative design of organizations-part III: modeling congruent, robust, and adaptive organizations
[J].DOI:10.1109/TSMCA.2003.822268 [本文引用: 1]
复杂网络系统拓扑连接优化控制方法
[J].
Control method for complex network topological connection optimization
[J].
Artificial bee colony algorithm for dynamic deployment of wireless sensor networks
[J].
Hybrid discrete artificial bee colony algorithm with threshold acceptance criterion for traveling salesman problem
[J].
Multiobjective discrete artificial bee colony algorithm for multiobjective permutation flow shop scheduling problem with sequence dependent setup times
[J].
Optimum assembly sequence planning system using discrete artificial bee colony algorithm
[J].
基于逻辑运算的离散人工蜂群算法
[J].DOI:10.3969/j.issn.0372-2112.2015.11.004 [本文引用: 1]
Discrete artificial bee colony algorithm based on logic operation
[J].DOI:10.3969/j.issn.0372-2112.2015.11.004 [本文引用: 1]
基于信息流的军事通信网络抗毁性优化设计
[J].
Military communication network design for invulnerability optimization based on information flow
[J].