浙江大学学报(工学版)

浙江大学学报(工学版), 2019, 53(8): 1448-1456 doi: 10.3785/j.issn.1008-973X.2019.08.003

土木与建筑工程

基于混凝土塑性损伤模型的轨道板损伤规律

任娟娟,, 王吉, 李家乐, 邓世杰, 徐家铎, 李潇

Damage law of track slab based on concrete damaged plasticity model

REN Juan-juan,, WANG Ji, LI Jia-le, DENG Shi-jie, XU Jia-duo, LI Xiao

收稿日期: 2018-07-8  

Received: 2018-07-8  

作者简介 About authors

任娟娟（1983—），女，教授，从事高速重载轨道结构与轨道动力学研究.orcid.org/0000-0003-4104-7385.E-mail：jj.ren@home.swjtu.edu.cn , E-mail：jj.ren@home.swjtu.edu.cn

摘要

基于混凝土塑性损伤模型，建立CRTS Ⅰ型轨道板损伤分布计算模型，将Tekscan传感器测得的钢轨支点压力作为荷载输入，以轨道板竖向位移及拉伸损伤因子作为评价指标，分析客货共线条件下水泥乳化沥青（CA）砂浆离缝状态时锚穴周边轨道板上表面混凝土的内部损伤规律. 结果表明：随着离缝长度的不断扩展，损伤产生及完全损伤的临界离缝高度均逐渐变小；当离缝长度扩展至第2、3锚穴时，客车荷载下损伤产生的临界离缝高度分别约为0.8、1.0 mm，货车荷载下约为0.5、0.8 mm；一旦超出损伤产生的临界离缝高度，由于轨道板损伤的发展，轨道结构整体抗弯刚度迅速降低导致板端竖向位移迅速增大；对于客车荷载，当离缝扩展至第3锚穴且高度大于1.0 mm后，CA砂浆形成脱空，板端位移不再增长，对于货车荷载，当离缝扩展至第3锚穴且高度大于1.3 mm后，由于二次损伤带的产生，板端竖向位移随离缝高度的增大迅速增大.

关键词： 混凝土塑性损伤模型 ; 客货共线 ; CRTS Ⅰ型板式无砟轨道 ; 砂浆离缝 ; 轨道板

Abstract

Based on the concrete damaged plasticity model, a CRTS Ⅰ track slab’s damage distribution model was established. The rail supporting force measured by Tekscan sensor was taken as load data, and the vertical displacement of track slab and the tensile damage factors were taken as calculating indicators. The inner damage law of the upper surface of track slabs near anchor pockets was analyzed when the debonding was between cement and emulsified asphalt (CA) mortar and track slabs existed in the passenger-freight line. Results showed that the critical heights of debonding for both initial damage and complete damage gradually decreased with the extension of the debonding length. When the debonding reached to the second and third anchor pockets, the critical heights of initial damage generated by the load under passenger car were about 0.8 mm and 1.0 mm, respectively; meanwhile, the critical heights under freight car were about 0.5 mm and 0.8 mm, respectively. Once the height of the debonding was greater than the critical height of initial damage, due to the development of the damage of track slab, the overall bending stiffness of the track structure decreased rapidly, resulting in a rapid increase of the vertical displacement of the slab end. Under the load of passenger car, after the debonding reached to the third anchor pocket and the height of the debondong was more than 1.0 mm, the CA mortar was formed into a void, and the displacement of the slab end did not increase any more. Under the load of freight car, when the debonding reached to the third anchor pocket and the height of the debonding was more than 1.3 mm, the vertical displacement of the slab end increased rapidly with the increase of the height of the debonding, due to the generation of the secondary damage zone.

Keywords： concrete damaged plasticity model ; passenger-freight line ; CRTS Ⅰ slab track ; debonding ; track slab

PDF (3344KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

任娟娟, 王吉, 李家乐, 邓世杰, 徐家铎, 李潇. 基于混凝土塑性损伤模型的轨道板损伤规律. 浙江大学学报(工学版)[J], 2019, 53(8): 1448-1456 doi:10.3785/j.issn.1008-973X.2019.08.003

REN Juan-juan, WANG Ji, LI Jia-le, DENG Shi-jie, XU Jia-duo, LI Xiao. Damage law of track slab based on concrete damaged plasticity model. Journal of Zhejiang University(Engineering Science)[J], 2019, 53(8): 1448-1456 doi:10.3785/j.issn.1008-973X.2019.08.003

无砟轨道具有高平顺性、高稳定性、良好的耐久性和少维修的特点[1]，为了缓解我国铁路运输压力，提升铁路运输质量，部分无砟轨道线路采用客货共线模式运营[2]. 在客货共线条件下，相较于客车，货车具有更大的轴重及运量，两者的荷载特征差异势必影响无砟轨道损伤的发展，例如在我国广泛应用的CRTS Ⅰ型板式无砟轨道. 该轨道为层状结构体系，其低弹性模量（E=100~300 MPa）的水泥乳化沥青砂浆（cement and emulsified asphalt mortar，CA砂浆）对轨道板的约束相对较弱，两者之间易形成离缝[3]. 在轨道结构长期服役过程中，砂浆离缝的不断扩展会极大削弱对轨道板的支承作用，加剧轨道板的损伤发展速度， 其中在客货混跑状态下CA砂浆与轨道板的损伤更为突出[4-5]. 由于张拉预留孔的设置，轨道板锚穴部位处的轨道板厚度较小，相比于轨道板其他部位，该处更容易产生损伤. 因此，当离缝扩展至轨道板锚穴部位时，轨道板产生损伤的可能性更大. 混凝土作为轨道板的主要材料，具有组成复杂、多孔性、均质性差、极限应变小等特点. 在无砟轨道的运营过程中混凝土的损伤规律尚不明确，故有必要引入适当的本构理论来分析客货共线条件下砂浆离缝对锚穴位置处轨道板损伤状况的影响，以探究砂浆离缝条件下轨道板的损伤规律.

为了探究混凝土结构在荷载作用下微孔洞、微裂纹萌生和扩展导致的材料损伤劣化行为，Lubliner等[6]基于损伤力学，首次提出混凝土塑性损伤（concrete damaged plasticity，CDP）模型概念，经实验验证该模型能反映混凝土的刚度退化效应及裂纹的萌生及扩展情况；Lee等[7]对Lubliner等[6]的成果展开进一步研究，建立混凝土循环受荷作用下的塑性损伤模型，通过数值计算验证了模型的可靠性. 目前，混凝土塑性损伤模型已有较为成熟的应用，但在无砟轨道领域的应用尚浅.

关于无砟轨道的损伤问题，林红松[8]建立损伤函数描述道床裂纹的“车辆-轨道”耦合振动模型，分析裂纹位置对无砟轨道动力响应的影响；黄慧超等[9]通过建立含道床板贯通裂纹的双块式无砟轨道梁体模型，分析得到最不利荷载作用下轨道板修补材料的受力变形特征，以上研究均基于线弹性理论. 考虑到材料劣化是结构损伤的内在原因，方树薇[10]基于混凝土线弹性断裂力学和应用扩展有限元方法分析道床板裂纹尖端的应力强度因子及扩展情况. 刘建超[11]采用内聚力理论分析CRTSⅡ型板砂浆层界面的力学行为，得到温度梯度荷载作用下轨道板与砂浆层层间损伤的分布和发展情况. 朱胜阳等[12]采用混凝土塑性损伤模型分析变温和列车动荷载共同作用下道床板损伤的演变规律及道床板损伤对结构力学行为的影响. 目前尚未见到关于锚穴位置处Ⅰ型轨道板上表面损伤规律的研究. 因此，本研究以客货共线CRTS Ⅰ型板式无砟轨道为研究对象，基于损伤力学理论，应用混凝土塑性损伤模型，建立砂浆离缝状态时轨道板损伤分布模型，分析锚穴位置处轨道板上表面损伤随CA砂浆离缝状态的分布状况，以明确轨道板损伤规律，阐释锚穴附近轨道板上表面混凝土开裂的原因.

1. 基于损伤力学的混凝土塑性损伤模型

混凝土塑性损伤模型基于损伤力学理论发展而来，能够描述混凝土材料变形及损伤特性[13]，达到从微观角度出发探究材料宏观力学效应的目的[14]. 该模型通过引入损伤因子模拟混凝土刚度随损伤增大而降低的特性.

1.1. 混凝土塑性损伤模型理论

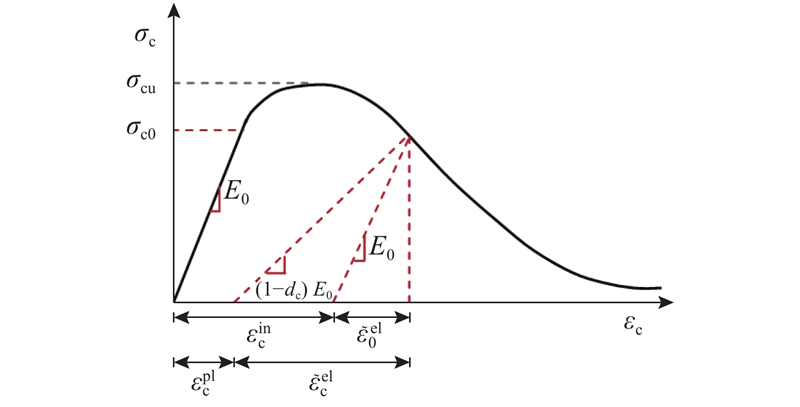
以单轴压缩行为为例，在混凝土塑性损伤模型中假定材料在屈服应力 $\sigma {}_{{\rm{c}}0}$之前为线弹性，当应力超过屈服应力后产生塑性硬化，直到应力超过极限应力 $\sigma {}_{{\rm{cu}}}$后，材料进入软化段[15]，如图1所示. 图中，斜率E0、（1−dc）E0分别为未考虑损伤时的卸载弹性模量和考虑损伤后的卸载弹性模量，针对此2种情况，对应的弹性应变分别为 $\tilde \varepsilon _0^{{\rm{el}}}$、 $\tilde \varepsilon _{\rm{c}}^{{\rm{el}}}$； $ \varepsilon _{\rm{c}}^{{\rm{in}}}$、 $ \varepsilon _{\rm{c}}^{{\rm{pl}}}$分别为非弹性应变和塑性应变； $\sigma_{\rm c} $为混凝土名义压缩压力； $\varepsilon _{\rm c}$为压缩应变.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   单轴压缩应力应变曲线

Fig.1   Stress-strain curve under uniaxial compression


混凝土名义压缩应力和有效压缩应力表达式分别为

$ {\sigma _{\rm{c}}} = \left( {1 - {d_{\rm c}}} \right){E_0}\left( {{\varepsilon _{\rm{c}}} - \varepsilon _{\rm{c}}^{{\rm{pl}}}} \right), $
(1)

$ {{\tilde \sigma} _{\rm{c}}} = {{{\sigma _{\rm{c}}}} / {(1 - {d_{\rm{c}}})}} = {E_0}({\varepsilon _{\rm{c}}} - \varepsilon _{\rm{c}}^{{\rm{pl}}}). $
(2)

式中： ${d_{\rm{c}}}$为单轴压缩损伤因子， ${E_0}$为混凝土无损伤弹性模量.

假定材料损伤后的弹性模量E可以通过E0与损伤因子d来表示：

$E = (1 - d){E_0}.$
(3)

损伤因子d是dc、拉伸损伤因子dt和应力状态的函数. 混凝土塑性损伤模型规定，在单轴循环荷载作用下，有

$1 - d = (1 - {s_{\rm{t}}}{d_{\rm{c}}})(1 - {s_{\rm{c}}}{d_{\rm{t}}}).$
(4)

式中：st、sc分别为与应力反向有关的刚度恢复应力状态的函数，表达式分别为

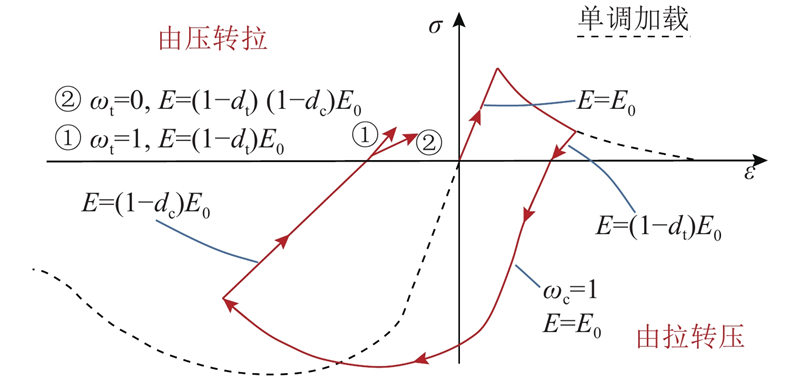
$ \left. \begin{array}{l} {s_{\rm{t}}} = 1 - {w_{\rm{t}}}r^*({\sigma _{11}});\;\;\;\;\;\;\;\;\;\;0 \leqslant {w_{\rm{t}}} \leqslant 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \\ {s_{\rm{c}}} = 1 - {w_{\rm{c}}}[1 - r^*({\sigma _{11}})]\;;\;\;0 \leqslant {w_{\rm{c}}} \leqslant 1,\\ r^*({\sigma _{11}}) = H({\sigma _{11}}) = \left\{ \begin{array}{l} 1,\;\;{\sigma _{11}} > 0;\\ 0,\;\;{\sigma _{11}} < 0. \end{array} \right. \end{array} \right\} $
(5)

其中，wt、wc为权重因子，用于控制反向加载下材料刚度的恢复. 如图2所示为单轴往复荷载（拉伸-压缩-拉伸）作用下塑性损伤模型弹性模量恢复示意图. 取wc=1，wt=0，分别表示混凝土由受拉转入受压时刚度可完全恢复和混凝土由受压转入受拉时刚度不能恢复，此时应力应变曲线如图中红色实线所示.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   CDP 模型在往复荷载作用下的弹性模量恢复示意图

Fig.2   Schematic diagram of elasticity modulus recovery of CDP model under reciprocating load


1.2. 损伤因子确定

准确定义混凝土塑性损伤模型的本构关系及损伤因子是描述混凝土塑性损伤的关键. 在该本构关系基础上引入损伤因子的概念，由式（3）可得，当材料受压时，混凝土单轴有效受压应力-应变关系为

${{\rm{\sigma }}_{\rm{c}}} = \left( {1 - {d_{\rm{c}}}} \right){E_0}{\varepsilon _{\rm{c}}}.$
(6)

根据《混凝土结构设计规范GB50010-2010》[16]，有

$ \left. {\begin{array}{l} {d_{\rm{c}}} = \left\{ {\begin{array}{*{20}{l}} {1 - {\rho _{\rm{c}}}n/(n - 1 + {x^n}),\quad\quad x \leqslant {\rm{1 }}};\\ {1 - {\rho _{\rm{c}}}/({a_{\rm{c}}}{{(x - 1)}^2} + x), \quad x > {\rm{1}}} ,\end{array}} \right.\\ x = \displaystyle\frac{\varepsilon }{{{\varepsilon _{{\rm{c}},{\rm{r}}}}}},\;\;\; n = \displaystyle\frac{{{E_0}{\varepsilon _{{\rm{c}},{\rm{r}}}}}}{{{E_0}{\varepsilon _{{\rm{c}},{\rm{r}}}} - {f_{{\rm{c}},{\rm{r}}}}}},\;\;\;{\rho _{\rm c}} = \displaystyle\frac{{{f_{{\rm{c}},{\rm{r}}}}}}{{{E_0}{\varepsilon _{{\rm{c}},{\rm{r}}}}}}. \end{array}} \right\} $
(7)

式中：ac为单轴受压本构关系曲线下降段参数，fc,r为单轴抗压强度代表值， ${\varepsilon _{{\rm{c}},{\rm{r}}}}$为混凝土峰值压应变.

假设非弹性应变 $\varepsilon _{\rm{c}}^{{\rm{in}}}$中塑性应变 $\varepsilon _{\rm{c}}^{{\rm{pl}}}$所占的比例为 $\;\beta _{\rm{c}}^{}$，得到压缩损伤因子的表达式[17]为

$ {d_{\rm{c}}} = \frac{{(1 - {\beta _{\rm{c}}})\varepsilon _{\rm{c}}^{{\rm{in}}}{E_0}}}{{{\sigma _{\rm{c}}} + (1 - {\beta _{\rm{c}}})\varepsilon _{\rm{c}}^{{\rm{in}}}{E_0}}}. $
(8)

拉伸损伤因子的计算方法与之类似：

${d_{\rm{t}}} = \frac{{\left( {1 - {\beta _{\rm{t}}}} \right)\varepsilon _{\rm{t}}^{{\rm{in}}}{E_0}}}{{{\sigma _{\rm{t}}} + \left( {1 - {\beta _{\rm{t}}}} \right)\varepsilon _{\rm{t}}^{{\rm{in}}}{E_0}}}.$
(9)

式中：当 $\;\beta _c^{}$=0.6， $\;\beta _t^{}$=0.9时，模型收敛性较好.

非弹性应变 $\varepsilon _{\rm{c}}^{{\rm{in}}}$和开裂应变 $\varepsilon _{\rm{t}}^{{\rm{in}}}$表达式分别为

$ \varepsilon _{\rm{c}}^{{\rm{in}}} = {\varepsilon _{\rm{c}}} - {\sigma _{\rm{c}}}/{E_0},\;\varepsilon _{\rm{t}}^{{\rm{in}}} = {\varepsilon _{\rm{t}}} - {\sigma _{\rm{t}}}/{E_0}. $
(10)

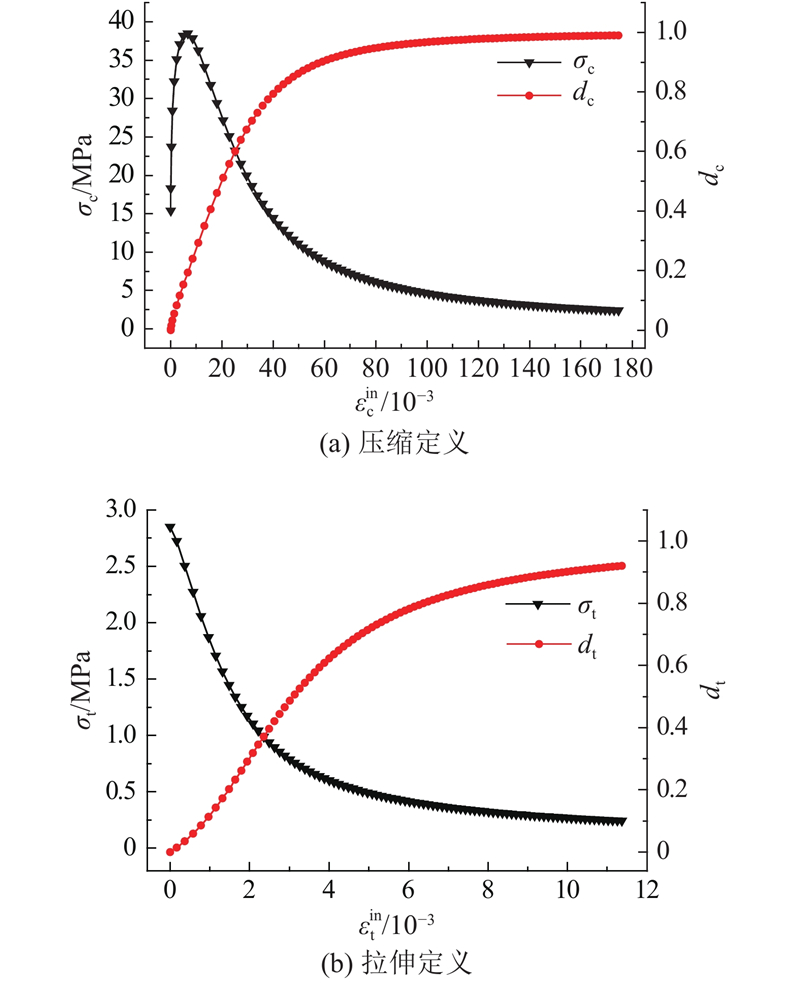
根据式（6）~（10），计算得到压缩（拉伸）时，轨道板所用C60混凝土的 $\varepsilon _{\rm{c}}^{{\rm{in}}}$（ $\varepsilon _{\rm{t}}^{{\rm{in}}}$）、 ${\sigma _{\rm{c}}}$（拉伸屈服应力 ${\sigma _{\rm{t}}}$）和dc（dt）之间的关系，如图3所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   C60混凝土塑性损伤模型定义曲线

Fig.3   Definition curve of CDP model for C60 concrete


2. 砂浆离缝状态下轨道板损伤分布模型

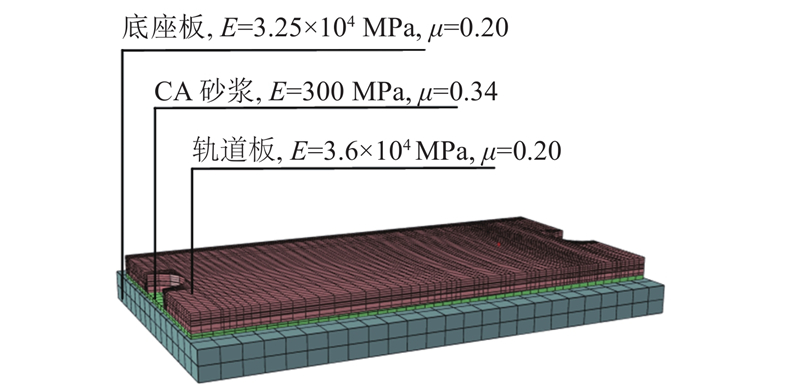
2.1. 轨道板损伤分布模型

将前文计算所得的 $\varepsilon _{\rm{c}}^{{\rm{in}}}$、 $\sigma $、d录入ABAQUS塑性损伤计算模型，建立不同砂浆离缝长度和高度下的轨道板损伤分布模型. 损伤分布模型的轨道板、砂浆层、底座板均采用实体单元，离缝处不建立任何单元，离缝以外的层间区域通过协调位移的黏结方式处理；在底座板下表面施加竖向位移约束，在底座板侧面施加纵向位移约束；预应力钢棒和普通钢筋均采用桁架单元，忽略预应力的损失，采用降温法来施加预应力，并假设钢棒预应力直接施加在轨道板锚穴相应位置处. 普通钢筋以无滑移的黏结方式和轨道板建立联系；轨道板受凸台纵横向约束；离缝处砂浆和轨道板间设置有限滑动硬接触来模拟两者间的法向作用. 所建有限元模型及主要结构参数如图4所示. 图中，E为弹性模量， $\mu$为泊松比.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   CRTS I型无砟轨道有限元模型

Fig.4   Finite element model of CRTS I slab track


离缝设置在板端位置，且横向贯通，工况设置如下：以长度d和高度h表示其几何尺寸. 长度分别为离缝扩展至第1、2、3锚穴位置时的距离；高度根据CRTS Ⅰ型板式无砟轨道层间离缝损伤评定建议[18]以及现场调研实际情况，取0.5、0.8、1.0、1.3、1.5 mm进行计算. 当砂浆离缝扩展至第1锚穴位置处时，状态示意图如图5所示[19]，其中荷载施加在板端第一扣件位置处.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   CRTS I型板式无砟轨道砂浆离缝示意图

Fig.5   Debonding schematic diagram of CRTS I slab track


2.2. 钢轨支点压力施加

为了获取客、货车钢轨支点压力F的分布范围，并为计算模型提供数值依据，引进美国研发的新型Tekscan薄膜压力传感器[20]对遂渝线蔡家车站段和渝怀线鱼嘴2号隧道处进行钢轨支点压力测试，如图6所示. 如图7所示为Tekscan压力传感器整体图.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   钢轨支点压力现场测试

Fig.6   Field test for rail supporting force


图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   5040N型号Tekscan压力传感器

Fig.7   5040N Tekscan pressure sensor


在遂渝线共测得客车数据26组，在渝怀线共测得客、货车数据29组，客车和货车的轴重、速度以及车辆状况均不同. 其中，客车轴重约为14 t，速度为55~120 km/h；货车轴重约为25 t，速度为60~100 km/h. 常用客车转向架为209型转向架，固定轴距为2.4 m，常用货车转向架为转K6型转向架，固定轴距为1.8 m. 为了研究最不利荷载下轨道板锚穴周边混凝土的损伤情况，选取实测得到的客、货车钢轨支点压力时程曲线中转向架荷载最大的一段，如图8红框所示，客、货车钢轨支点压力最大值分别为71.71、101.58 kN. 采用准静态加载方式模拟列车荷载的单点时程特性[21].

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   实测钢轨支点压力时程曲线

Fig.8   Time history curve of tested rail supporting force


3. 离缝状态下轨道板动力特性及损伤分布

以轨道板竖向位移y以及混凝土拉伸损伤因子dt为主要指标，计算分析离缝分别扩展至第1、2、3锚穴位置且离缝高度h分别为0.5、0.8、1.0、1.3、1.5 mm时，在客、货车荷载作用下，I型轨道板端部竖向动态位移、锚穴周边轨道板上表面混凝土的损伤规律及分布状况.

3.1. 轨道板上表面损伤因子

如图9所示为在荷载时程曲线加载下出现并达到最大损伤的轨道板损伤分布图. 由图9（a）可以看出，当离缝扩展至第2锚穴时，在货车荷载作用下，当h=0.8 mm时，轨道板不再处于弹性受力阶段，开始出现损伤，其中最大损伤因子dt,max=0.25；当h=1.0 mm时，dt迅速增大至1.00，离缝根部位置处轨道板上表面部分区域已达到完全损伤. 由图9（b）可以看出，当离缝扩展至第3锚穴时，在客车荷载作用下，当h=1.0 mm时，轨道板上表面部分区域达到完全损伤. 由图9（c）可以看出，当离缝扩展至第3锚穴时，在货车荷载作用下，当h=0.8 mm时，轨道板上表面离缝根部相应位置处大部分区域已达到完全损伤，且随着离缝高度的增加，损伤带迅速扩展，在h=1.3 mm时开始形成二次损伤带，且二次损伤带中也有部分区域完全损伤.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   不同工况下轨道板最大损伤分布

Fig.9   Maximum damage distribution of track slab under different cases


为了更好地分析轨道板上表面的损伤规律，取不同离缝状态下客、货车通过时轨道板上表面最大损伤因子，得到损伤因子影响因素的插值曲面图，如图10所示. 图中，n=1、2、3分别为离缝扩展至第1、2、3锚穴位置（l=346、586、826 mm）时的情况.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   轨道板损伤因子的影响因素

Fig.10   Influence factors of track slab damage factor


由图10（a）可知，在客车荷载下，当离缝扩展至第1锚穴时，轨道板上表面始终有dt=0，离缝高度变化不会导致轨道板产生损伤；随着离缝长度不断扩展，损伤产生（dt>0）的临界离缝高度逐渐变小，当离缝扩展到第2锚穴后，损伤产生的临界离缝高度随离缝扩展长度的变化趋于平缓，此时损伤产生的临界离缝高度约为0.8 mm；当离缝高度大于损伤产生的临界离缝高度后，损伤因子随离缝高度的增大显著增长，且离缝扩展长度越大，损伤因子随离缝高度的变化越剧烈；随着离缝长度不断扩展，混凝土材料损伤完全（dt=1）的临界离缝高度也随离缝长度的扩展而逐渐变小，其中当离缝扩展至第1至第2锚穴中间时，损伤完全的临界离缝高度约为1.2 mm，当离缝扩展至第3锚穴时，损伤完全的临界离缝高度约为1.0 mm.

由图10（b）可知，在货车荷载下，当离缝扩展至第1锚穴时，损伤产生（dt>0）的临界离缝高度为1.0 mm；随着离缝长度的不断扩展，损伤产生（dt>0）的临界离缝高度逐渐变小，当离缝扩展至第2锚穴后，损伤产生的临界离缝高度随离缝扩展长度的变化趋于平缓，此时损伤产生的临界离缝高度约为0.6 mm；当离缝高度大于损伤产生的临界离缝高度后，损伤因子随离缝高度的增大显著增长，且离缝扩展长度越大，损伤因子随离缝高度的变化越剧烈；随着离缝长度不断扩展，混凝土材料损伤完全（dt=1）的临界离缝高度也随离缝长度的扩展逐渐变小，其中当离缝扩展至第1锚穴时，轨道板区域内不会出现完全损伤（dt=1），当离缝扩展至第1至第2锚穴中间时，损伤完全的临界离缝高度约为1.2 mm，当离缝扩展至第3锚穴时，损伤完全的临界离缝高度约为0.8 mm.

3.2. 轨道板端部竖向位移

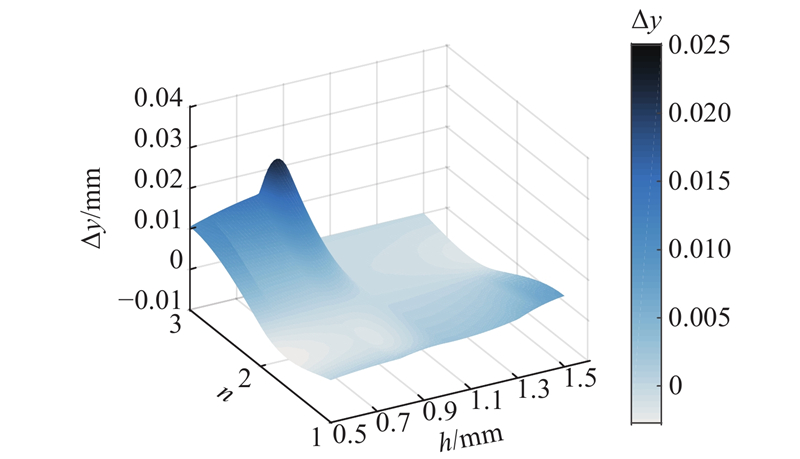
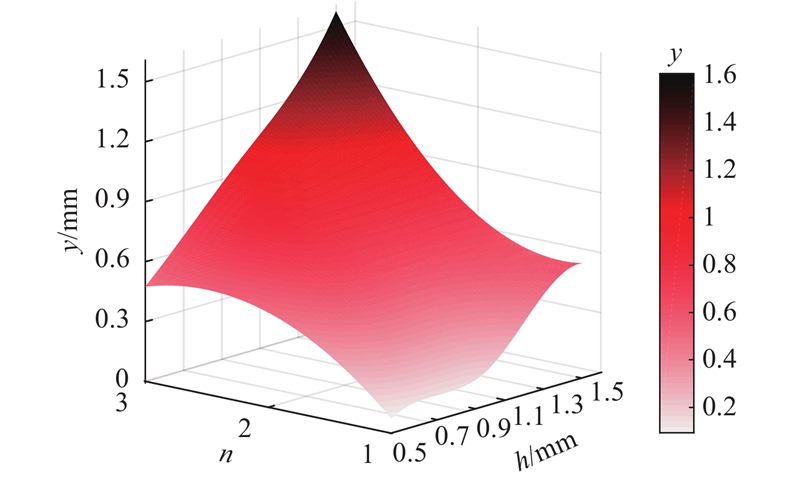
当离缝扩展至第3锚穴，h=0.5、0.8、1.0、1.3 mm时，客货车荷载下轨道板板端竖向位移y的时程曲线如图11所示. 由图11（a）可以看出，在客车荷载下，当离缝扩展至第3锚穴，h=0.5、0.8、1.0 mm时，轨道板端部竖向位移略大于离缝高度，说明离缝处CA砂浆层对轨道板产生支承作用；当h≥1.0 mm后，轨道板端部竖向位移曲线基本重合，表明y基本稳定，且最大竖向位移出现在h=1.3 mm时，为ymax=1.06 mm，说明离缝处CA砂浆完全失去支承. 由图11（b）可以看出，在货车荷载下，当离缝扩展至第3锚穴时，轨道板端部竖向位移均略大于离缝高度，说明离缝处CA砂浆层对轨道板产生支承作用.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   客、货车荷载作用下轨道板端部竖向位移的时程曲线

Fig.11   Time history curves of track slab end vertical displacement under loads of passenger car and freight car


为了更好地分析离缝状态对轨道板端位移的影响，取不同离缝状态下客、货车通过时轨道板板端的垂向动态位移最大值，得到板端位移y影响因素的插值曲面图以及板端位移变化率Δy的插值曲面图，如图12~15所示.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   客车荷载下的板端竖向位移

Fig.12   Vertical displacement of slab end under load of passenger car


图 13

新窗口打开| 下载原图ZIP| 生成PPT

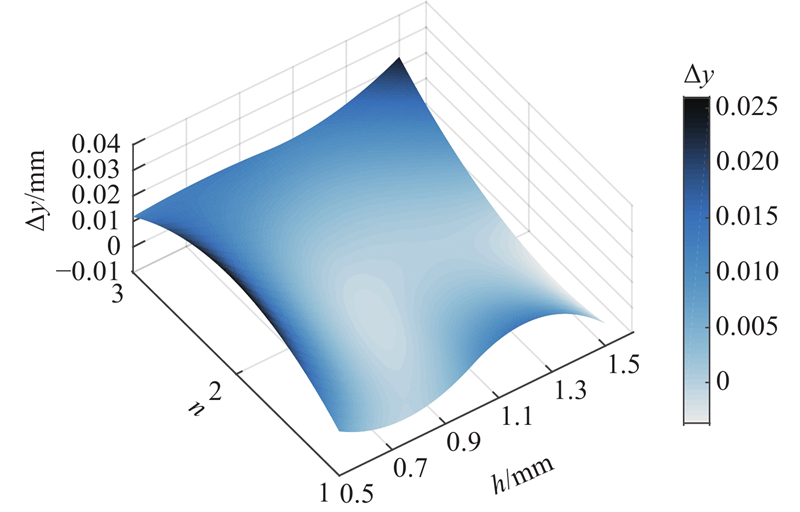
图 13   客车荷载下的板端竖向位移变化率

Fig.13   Vertical displacement change rate of slab end under load of passenger car


图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   货车荷载下的板端竖向位移

Fig.14   Vertical displacement of slab end under load of freight car


图 15

新窗口打开| 下载原图ZIP| 生成PPT

图 15   货车荷载下的板端竖向位移变化率

Fig.15   Vertical displacement change rate of slab end under load of freight car


由图12、13可知，在客车荷载下，当离缝扩展至第1锚穴时，随离缝高度增大，轨道板端竖向位移随离缝高度变化的增长率略有增大，离缝高度对轨道板端竖向位移的影响较小. 随着离缝向第3锚穴扩展，离缝高度对轨道板板端竖向位移的影响不断增大，当离缝扩展至第3锚穴，h=0.8~1.0 mm时，轨道板端竖向位移随离缝高度的增长率达到最大值，通过对比损伤因子影响图可知，该离缝高度区间正好为轨道板损伤产生的临界离缝高度至损伤完全的临界离缝高度. 该现象能解释在轨道板损伤后，轨道结构整体抗弯刚度迅速降低导致板端竖向位移迅速增大的规律，当h>1.0 mm后，轨道板部分区域已完全破坏，但由于离缝高度大于轨道板端竖向位移，CA砂浆形成脱空，轨道板端竖向位移不再随离缝高度的增长而增大.

由图14、15可知，在货车荷载且离缝扩展至第1锚穴的情况下，当h<1.0 mm时，离缝高度对板端竖向位移的影响较小，当h=1.0~1.3 mm时，轨道板端竖向位移随离缝高度变化的增长率略有增大，在该离缝高度区间内，混凝土轨道板出现损伤，损伤发展导致板端竖向位移迅速增大；随着离缝不断向第3锚穴扩展，离缝高度对轨道板端竖向位移的影响不断增大，当离缝扩展至第2锚穴，h=0.5~1.0 mm时，轨道板端竖向位移随离缝高度的增长率较大，通过对比损伤因子影响图可知，该离缝高度区间正好对应着轨道板损伤产生的临界离缝高度至损伤完全的临界离缝高度，此后，由于离缝高度大于板端竖向位移，CA砂浆形成脱空，轨道板端竖向位移不再随离缝高度的增长而增大；当离缝扩展至第3锚穴，h=0.5~1.0 mm时，轨道板端竖向位移随离缝高度的增长率较离缝在第2锚穴位置时有较大的提升，这是由于随着离缝长度的扩展，损伤产生的临界离缝高度更小，当h>1.3 mm后，由于二次损伤带的产生，板端竖向位移随离缝高度变化的增长率再次增大.

4. 结　论

（1）在客货共线条件下，随着离缝长度的不断扩展，混凝土损伤产生（dt>0）的临界离缝高度以及完全损伤（dt=1）的临界离缝高度逐渐变小；在相同离缝高度下，离缝扩展越长，损伤发展速率越快.

（2）当离缝长度扩展至第2锚穴后，混凝土损伤产生（dt>0）的临界离缝高度基本达到稳定，在客车荷载和货车荷载下损伤产生（dt>0）的临界离缝高度分别约为0.8、0.5 mm；当离缝长度扩展至第1至第2锚穴之间时，在一定离缝高度下轨道板局部区域将出现完全损伤（dt=1），当离缝扩展至第3锚穴时，在客车荷载和货车荷载下完全损伤的临界离缝高度分别约为1.0、0.8 mm.

（3）在客、货车荷载下，随着离缝长度的不断扩展，离缝高度对轨道板端竖向位移的影响不断增大，当离缝高度大于损伤产生的临界离缝高度后，由于轨道板损伤发展，轨道结构整体抗弯刚度迅速降低导致板端竖向位移迅速增大.

（4）对于客车荷载，当离缝长度扩展至第3锚穴且离缝高度大于1.0 mm后，CA砂浆形成脱空，轨道板损伤和轨道板端竖向位移不再随离缝高度的增长而增大；对于货车荷载，当离缝长度较大，离缝高度大于1.3 mm后，由于二次损伤带的产生，板端竖向位移随离缝高度变化的增长率再次增大.

（5）建议离缝尺寸一旦接近上述临界值立刻采取修补措施，以避免轨道结构进一步损伤.

参考文献

任娟娟, 田根源, 徐家铎, 等

客货共线单元板式无砟轨道荷载作用特性与疲劳寿命预测

[J]. 铁道学报, 2019, 41 (3): 110- 116

DOI:10.3969/j.issn.1001-8360.2019.03.015      [本文引用: 1]

REN Juan-juan, TIAN Gen-yuan, XU Jia-duo, et al

Load effect and fatigue life prediction of prefabricated slab track for mixed passenger and freight railway

[J]. Journal of the China Railway Society, 2019, 41 (3): 110- 116

DOI:10.3969/j.issn.1001-8360.2019.03.015      [本文引用: 1]

REN J J, DENG S J, WEI K, et al

Mechanical property deterioration of the prefabricated concrete slab in mixed passenger and freight railway tracks

[J]. Construction and Building Materials, 2019, 208: 622- 637

DOI:10.1016/j.conbuildmat.2019.03.039      [本文引用: 1]

REN J J, LI X, YANG R S, et al

Criteria for repairing damages of CA mortar for prefabricated framework-type slab track

[J]. Construction and Building Materials, 2016, 110: 300- 311

DOI:10.1016/j.conbuildmat.2016.02.036      [本文引用: 1]

齐少轩, 任娟娟, 刘学毅

桥上CRTS II型道岔板砂浆离缝影响特性研究

[J]. 工程力学, 2015, (6): 124- 132

[本文引用: 1]

QI Shao-xuan, REN Juan-juan, LIU Xue-yi

Influence of debonding on the performance of CRTS II slab track turnouts on large bridges

[J]. Engineering Mechanics, 2015, (6): 124- 132

[本文引用: 1]

谢露, 赵春光, 苏乾坤, 等

轨道板与CA砂浆间拍打作用研究

[J]. 铁道科学与工程学报, 2017, 14 (4): 675- 681

DOI:10.3969/j.issn.1672-7029.2017.04.002      [本文引用: 1]

XIE Lu, ZHAO Chun-guang, SU Qian-kun, et al

Study on the flap action between slab and CA mortar

[J]. Journal of Railway Science and Engineering, 2017, 14 (4): 675- 681

DOI:10.3969/j.issn.1672-7029.2017.04.002      [本文引用: 1]

LUBLINER J, OLIVER J, OLLER S, et al

A plastic-damage model for concrete

[J]. International Journal of Solids and Structures, 1989, 25 (3): 299- 326

DOI:10.1016/0020-7683(89)90050-4      [本文引用: 2]

LEE J, FENVES G L

Plastic-damage model for cyclic loading of concrete structures

[J]. Journal of Engineering Mechanics, 1998, 124 (8): 892- 900

DOI:10.1061/(ASCE)0733-9399(1998)124:8(892)      [本文引用: 1]

林红松. 基于断裂和损伤力学的无砟轨道静动力特性研究[D]. 成都: 西南交通大学, 2009.

[本文引用: 1]

LIN Hong-song. Research on the static and dynamic property of ballastless track based on fracture and damage mechanics [D]. Chengdu: Southwest Jiaotong University, 2009.

[本文引用: 1]

黄慧超, 徐坤, 任娟娟

双块式无砟轨道连续道床板裂纹修复材料性能分析

[J]. 铁道标准设计, 2013, (12): 50- 53

[本文引用: 1]

HUANG Hui-chao, XU Kun, REN Juan-juan

Performance analysis of repair material for crack repairing of continuous track slab of bi-block ballastless track

[J]. Railway Standard Design, 2013, (12): 50- 53

[本文引用: 1]

方树薇. 北京地铁无砟轨道开裂机理及其对列车运营安全的影响研究[D]. 北京: 北京交通大学, 2014.

[本文引用: 1]

FANG Shu-wei. Study on crack mechanism of ballastless track and its impact on safety of train operation in Beijing metro [D]. Beijing: Beijing Jiaotong University, 2014.

[本文引用: 1]

刘建超. 温度荷载作用下CRTS Ⅱ 型板式无砟轨道砂浆层界面损伤分析[D]. 成都: 西南交通大学, 2016.

[本文引用: 1]

LIU Jian-chao. Damage analysis of cement asphalt mortar layers interface for CRTS II ballastless slab track [D]. Chengdu: Southwest Jiaotong University, 2016.

[本文引用: 1]

朱胜阳, 蔡成标

温度和列车动荷载作用下双块式无砟轨道道床板损伤特性研究

[J]. 中国铁道科学, 2012, 33 (1): 6- 12

DOI:10.3969/j.issn.1001-4632.2012.01.02      [本文引用: 1]

ZHU Sheng-yang, CAI Cheng-biao

Research on the damage characteristics of double-block ballastless track bed slab under temperature and vehicle dynamic loads

[J]. China Railway Science, 2012, 33 (1): 6- 12

DOI:10.3969/j.issn.1001-4632.2012.01.02      [本文引用: 1]

徐俊祥. 混凝土结构的损伤力学分析[D]. 南京: 河海大学, 2004.

[本文引用: 1]

XU Jun-xiang. Analysis of concrete structure based on damage mechanics [D]. Nanjing: Hohai University, 2004.

[本文引用: 1]

贾少文. 基于连续损伤力学的混凝土疲劳损伤模型[D]. 哈尔滨: 哈尔滨工业大学, 2009.

[本文引用: 1]

JIA Shao-wen. Continuum damage mechanics-based fatigue damage model for concrete [D]. Harbin: Harbin Institute of Technology, 2009.

[本文引用: 1]

薛明琛, 赵永生, 汤美安

断裂力学和损伤力学在混凝土中的应用

[J]. 山西建筑, 2007, 33 (36): 19- 20

DOI:10.3969/j.issn.1009-6825.2007.36.010      [本文引用: 1]

XUE Ming-chen, ZHAO Yong-sheng, TANG Mei-an

Fracture mechanics and damage mechanics application of concrete

[J]. Shanxi Architecture, 2007, 33 (36): 19- 20

DOI:10.3969/j.issn.1009-6825.2007.36.010      [本文引用: 1]

中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010−2010[S]. 北京: 中国建筑工业出版社, 2014: 211.

[本文引用: 1]

张劲, 王庆扬, 胡守营, 等

ABAQUS混凝土损伤塑性模型参数验证

[J]. 建筑结构, 2008, 38 (8): 127- 130

[本文引用: 1]

ZHANG Jing, WANG Qing-yang, HU Shou-ying, et al

Parameters verification of concrete damaged plastic model of ABAQUS

[J]. Building Structure, 2008, 38 (8): 127- 130

[本文引用: 1]

刘克飞. 框架型板式轨道水泥乳化沥青砂浆伤损及维修标准研究[D]. 成都: 西南交通大学, 2013.

[本文引用: 1]

LIU Ke-fei. Research on cement asphalt mortar damage and maintenance standards for frame type of slab track [D]. Chengdu: Southwest Jiaotong University, 2013.

[本文引用: 1]

徐光鑫. 预应力钢棒失效对CRTS Ⅰ 型单元轨道板受力性能的影响[D]. 成都: 西南交通大学, 2014.

[本文引用: 1]

XU Guang-xin. Study on pc steel bar's failure on unit of CRTS I slab track performance [D]. Chengdu: Southwest Jiaotong University, 2014.

[本文引用: 1]

赵华卫. 客货共线无砟轨道荷载作用特征分析[D]. 成都: 西南交通大学, 2017.

[本文引用: 1]

ZHAO Hua-wei. The train load characteristics for mixed passenger and freight railways with ballastless track [D]. Chengdu: Southwest Jiaotong University, 2017.

[本文引用: 1]

LEI X, ROSE J G

Track vibration analysis for railways with mixed passenger and freight traffic

[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2008, 222 (4): 413- 421

DOI:10.1243/09544097JRRT185      [本文引用: 1]

/

〈 〉