自从透空结构造波理论[4]提出以来,透空结构在海洋结构物设计的理论研究和工程实践中均获得了较广泛的应用. Manam等[5]利用解析方法分析竖直透空隔板的波浪散射问题,Zhao等[6-7]对圆形水平透空结构的波浪载荷及水动力性能进行解析研究;Williams等[7]分析中间段带有透空结构、上下两端均不透水的浮式柱体的水动力系数;岳景云等[8]在线性波浪理论下,采用复合边界元法分析入射波对内、外壁皆透空双层透水沉箱的作用;Cho[9]使用数值模拟的方法分析侧立透水孔板对浮式结构水动力性能的影响. 在工程实践方面,崔勇等[10]对渔业生产中的透空网箱在波流场中的动态响应进行数值模拟;Besio等[3]将透空结构引入海上风力发电基础围护问题中,开展理论和试验分析,同时,透空结构被引入垂荡型圆柱浮子式波浪能装置中,对垂荡水动力特性进行解析研究[11].
以上研究多集中于透空结构对固定式结构物或单自由度浮式结构物所受波浪载荷产生的影响. 本文针对含侧立透空结构的浮式结构物在3个自由度上(纵荡、垂荡、横摇)的波浪辐射问题,基于porous-wavemaker理论和二维势流理论,采用解析方法,构建计算模型,分析透空结构的透水能力对水动力系数的影响机理;将部分解析计算结果与文献[12]的数值计算结果进行对比分析,以验证理论解析模型的正确性.
1. 理论计算模型
如图1所示,一长度为
图 1
假设在有限水深的流场范围内,流体不可压缩且无黏性,浮体系统在纵荡、垂荡以及横摇3个自由度上作小幅受迫运动,运动方程如下:
式中:
以透空薄板为界限,将整个流场区域划分为3个子区域(如图1的I、II、III所示),
式中:
其中,
式中:
在流场区域边界
式中:
式中:
在边界
在边界
在边界
2. 理论模型解析求解
根据边界条件(4)~(6),利用分离变量法,求解拉普拉斯方程(3),可得速度势函数的表达式为
式中:
当
当
式中:
用一个趋近于无穷大的实数M替代累和符号中的“
式中:
其中,
3. 计算结果与分析
在解析计算的过程中,当速度势函数表达式中的级数截断项取值为40时,计算结果已经满足收敛要求,因此取
图 2
图 3
图 4
图 5
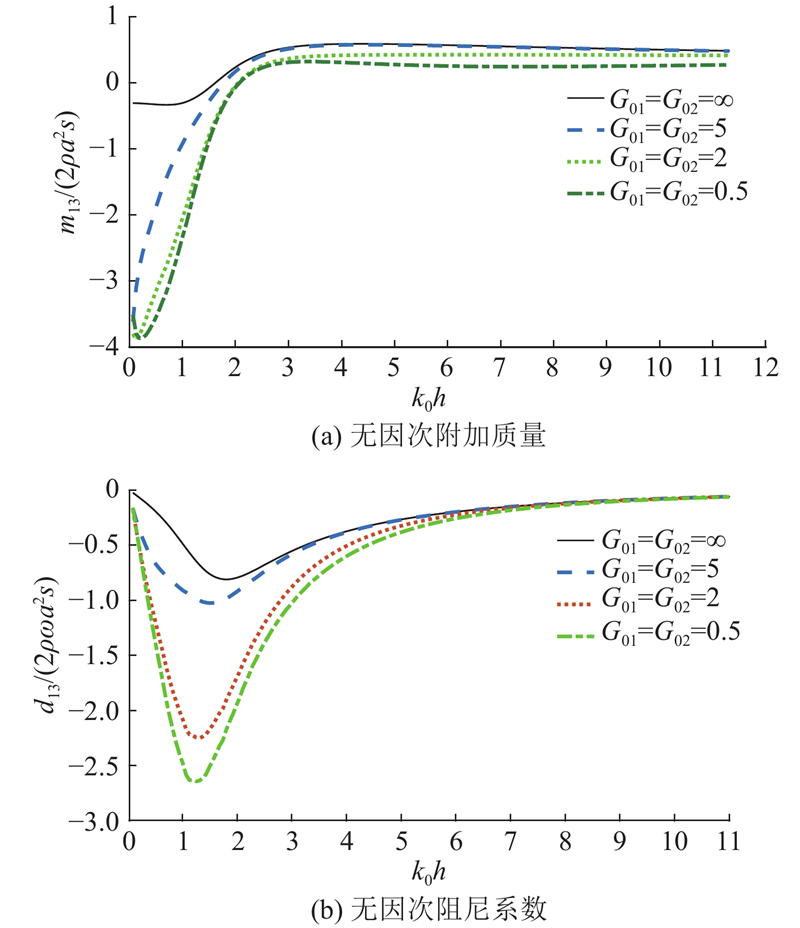
如图2~5所示,同时改变透空薄板A和B的透水系数后,浮体系统的无因次水动力系数均呈现出不同程度的变化:浮体系统在作小幅受迫运动时,随着透空薄板透水系数的增加,透空薄板的迎浪面积减小,浮体系统所受到的波浪激励力相应减小,导致浮体系统的附加质量系数和辐射阻尼系数均呈现减小趋势,尤其是在长波区域,减小趋势更明显. 对于纵荡方向上的水动力系数(见图2),当
图 6
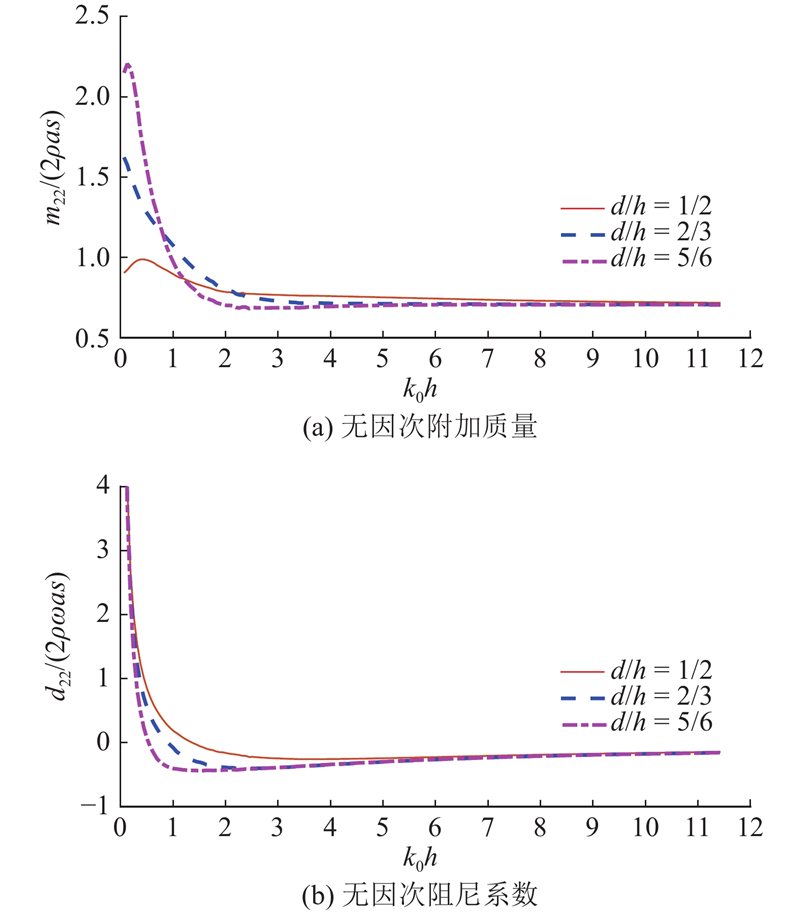
图 6 透空薄板水下深度对纵荡数值结果的影响
Fig.6 Influence of submerged depth of porous wall to hydrodynamic coefficients of surge-surge
图 7
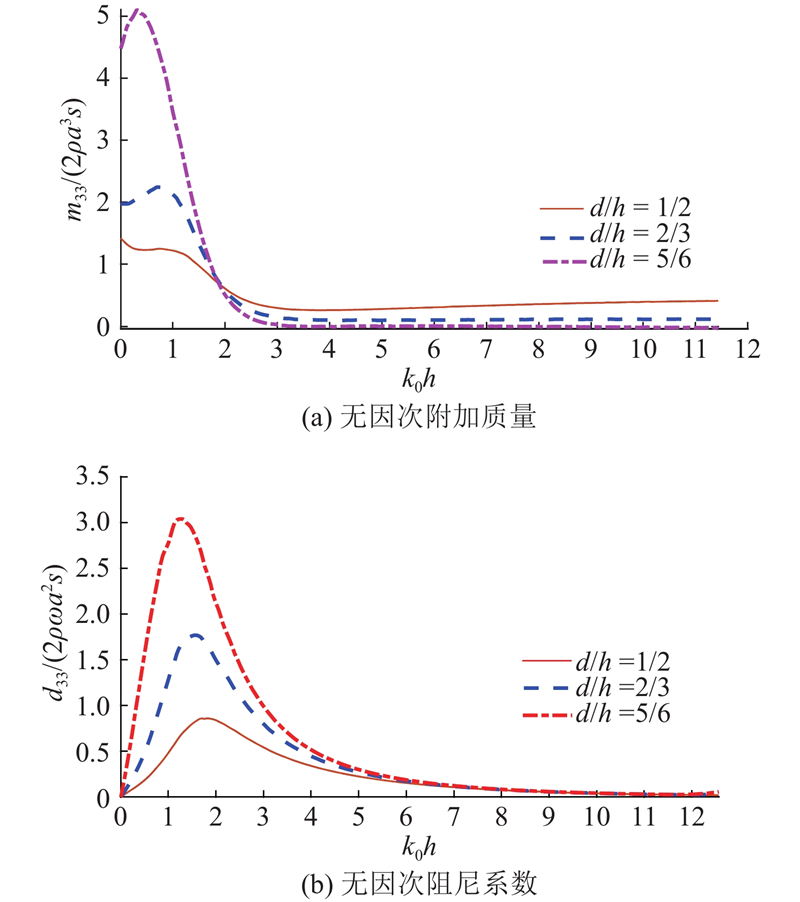
图 7 透空薄板水下深度对垂荡数值结果的影响
Fig.7 Influence of submerged depth of porous wall to hydrodynamic coefficients of heave-heave
图 8
图 8 透空薄板水下深度对横摇数值结果的影响
Fig.8 Influence of submerged depth of porous wall to hydrodynamic coefficients of roll-roll
4. 结 语
本文将透空薄板结构引入深水浮式结构物的设计中,针对带有侧立透空薄板的浮式结构物在3个自由度上的微幅受迫运动,建立水动力性能分析的解析计算模型. 研究结果表明,在低频区域(
参考文献
Scattering of water waves by a floating body with two vertically attached porous walls
[J].DOI:10.1061/(ASCE)EM.1943-7889.0001384 [本文引用: 1]
Wave absorbing system using in-clined perforated plates
[J].
Sediment transport patterns at Trafalgar offshore windfarm
[J].DOI:10.1016/j.oceaneng.2008.01.002 [本文引用: 2]
A porous–wavemaker theory
[J].
Scattering of water waves by vertical porous barriers: an analytical approach
[J].
Hydrodynamic loads acting on a circular porous plate horizontally sub merged in waves
[J].
Water wave interaction with a floating porous cylinder
[J].DOI:10.1016/S0029-8018(98)00078-X [本文引用: 2]
波浪与内外壁透空双层透水结构相互作用
[J].
Wave interaction with a concentric cylinder comprising dual porous structures
[J].
Transmission coefficients of a floating rectangu-lar breakwater with porous side plates
[J].DOI:10.1016/j.ijnaoe.2015.10.002 [本文引用: 1]
浮式鲆鲽类网箱在波流场中动态响应的数值模拟
[J].
Numerical simulation of floating flatfish cage behavior under waves and currents
[J].
波浪作用下上部带有透空结构的圆筒垂向水动力特性的解析研究
[J].
Analytical study on the vertical hydrodynamics of a trun-cated cylinder with upper porous wall and inner column
[J].
On the radiation and diffraction of water waves by a rectangular buoy
[J].
Water waves on flexible and porous breakwaters
[J].