浙江大学学报(工学版)

浙江大学学报(工学版), 2019, 53(7): 1380-1388 doi: 10.3785/j.issn.1008-973X.2019.07.018

交通工程、土木工程

基于部分抗剪的钢箱梁横向分块施工效应分析

汪劲丰,, 乌添媚, 王建江, 王敏权, 徐荣桥

Analysis of transverse separated-block construction effects of steel box girders based on partial shear theory

WANG Jin-feng,, WU Tian-mei, WANG Jian-jiang, WANG Min-quan, XU Rong-qiao

收稿日期: 2018-05-18  

Received: 2018-05-18  

作者简介 About authors

汪劲丰（1976—），男，副教授，从事桥梁施工方法及控制技术的研究.orcid.org/0000-0002-9099-818X.E-mail：wangjinfeng@zju.edu.cn , E-mail：wangjinfeng@zju.edu.cn

摘要

为了研究横向分块施工造成的抗剪刚度减弱且分布不均对分块钢箱梁受力特性的影响，针对分块后不对称开口薄壁构件顶、底板之间部分抗剪的力学特性，引入考虑界面滑移的组合结构理论，建立变形和应力的解析分析方法. 基于典型等截面单箱多室钢箱梁截面设计参数的统计规律进一步归并结构尺寸参数，建立以桥梁跨度、分段长度和抗剪刚度等关键参数为基本变量的变形计算公式. 通过影响参数分析，提出能够应用于不同跨度钢箱梁的分块施工方法. 结果表明，当分段长度增大到40 m以上时，必须采用抗剪临时撑增大抗剪刚度，或采用临时支点加固，以减小变形、控制施工质量.

关键词： 钢箱梁桥 ; 横向分块施工 ; 部分抗剪 ; 参数分析 ; 施工方法

Abstract

An analytical method for deformation and stress was established in order to analyze the effect of weakened and uneven shear rigidity caused by the transverse separated-block construction on the mechanical characteristics of separated-block steel box girders. The theory of composite structure considering slip at the interlayer was adopted based on the partial shear connection between the top and bottom plate of the asymmetrical thin-walled, open-section block after partition. The deformation equation based on the key parameters such as the span of the bridge, segment length and shear stiffness was established by analyzing the section design parameters from the typical single-box multi-cell steel box girder with constant sections, obtaining the statistical law and eliminating some geometric parameters. The block construction method, which can be applied to steel box girder with different spans, was proposed by analyzing the impact parameters. Results show that temporary shear braces should be used to increase the shear stiffness, or a temporary pier is required to reduce the deflection and control the construction quality when the segment length exceeds 40 m.

Keywords： steel box girder ; transverse separated-block construction ; partial shear ; parameter analysis ; construction method

PDF (1725KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

汪劲丰, 乌添媚, 王建江, 王敏权, 徐荣桥. 基于部分抗剪的钢箱梁横向分块施工效应分析. 浙江大学学报(工学版)[J], 2019, 53(7): 1380-1388 doi:10.3785/j.issn.1008-973X.2019.07.018

WANG Jin-feng, WU Tian-mei, WANG Jian-jiang, WANG Min-quan, XU Rong-qiao. Analysis of transverse separated-block construction effects of steel box girders based on partial shear theory. Journal of Zhejiang University(Engineering Science)[J], 2019, 53(7): 1380-1388 doi:10.3785/j.issn.1008-973X.2019.07.018

随着城市交通需求的日益增长，建造城市高架桥成为发展立体交通、缓解拥堵问题的有效方式[1]. 高架桥多位于城市中心枢纽地带，施工空间和工期受到极大限制[2]. 单箱多室连续钢箱梁桥凭借更优的跨越能力和抗弯抗扭刚度，逐渐替代传统预应力混凝土梁桥成为城市高架的优势桥型. 针对高架桥施工须减少交通干扰且吊装能力受限的难点，采用横向分块施工，即沿横桥向将完整截面切割为多个单箱室截面，进行分块整跨吊装，实现了城市高架桥的快速架设[3-5].

横向分块使对称封闭的钢箱梁变成多片不对称开口薄壁截面，导致吊装时钢箱梁容易发生局部屈曲，施工质量难以控制[6-7]. 如Biezma等[8-9]在对墨尔本西门大桥事故的研究中发现是由于分块吊装施工时发生局部屈曲而倒塌. 虽然通过减小开口箱梁块长度能够改善变形和受力，但会相应地增加纵向分段数和临时墩数量，严重影响桥下交通和施工效率. 根据钢箱梁构造及实际安装条件评估横向分块施工方案尤为重要，但缺乏相应的指导准则.

横向分块后的开口截面钢箱梁顶底板之间由完全抗剪约束变为部分抗剪连接，顶底板之间容易发生相对滑移，可以将其看作考虑界面滑移的广义组合结构. 学者们针对该结构的受力特性开展了大量研究：蒋丽忠等[10]等利用古德曼弹性夹层假设，推导均布荷载下简支组合梁界面滑移和挠度变形的理论计算公式；刘寒冰等[11]基于接触理论，推导在竖向荷载作用下考虑剪切滑移效应的组合梁位移和应变的解析解；苗林等[12]通过“滑移附加弯矩”计算梁在各种荷载约束条件下的内力、滑移和挠度分布规律；Xu等[13-15]提出组合梁的二维分析理论，分析基于Timoshenko梁理论假设的部分抗剪连接组合结构的静动力特性；Zona等[16]研究抗剪连接件的分布对界面滑移的影响. 上述成果为本文研究奠定了良好的理论基础.

本文将考虑界面滑移的组合结构理论应用于横向分块后的钢箱梁块，引入部分抗剪组合结构的控制微分方程，求解变形和应力. 根据横向分块后钢箱梁块的构造特点，归纳分析影响位移和应力的关键参数及影响规律，进行分块施工技术探讨，并指导和应用于工程实例.

1. 部分抗剪连接组合结构理论的基本假设及求解

1.1. 基本假设

钢箱梁横向分块后顶底板失去位移连续的约束条件，开口箱梁可以当作是由顶板、底板组成的双层结构，其中顶板即钢箱梁的顶板，底板由钢箱梁的底板与腹板组成. 假设[17]：1）组合结构材料在荷载作用下线弹性变化且均为小变形；2）顶底板分别满足平截面假定；3）顶底板间的抗剪刚度连续且沿梁长方向均匀分布，且界面滑移力与相对滑移成正比；4）顶底板曲率相同，不发生横向的相对位移.

1.2. 计算过程

组合结构受横向荷载作用时，微元体受力模型如图1所示. 图中，Ei、Ai、Ii（i=1，2）分别为上、下两部分的弹性模量、截面积和惯性矩；q为横向荷载；Q、M为外荷载在x截面处产生的剪力和弯矩；Ni、Qi、Mi（i=1，2）分别为组合结构上、下两部分的轴力、剪力和弯矩；Qs为交界面的滑移力；h1、h2为上、下两部分形心到上、下缘的距离.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   组合结构微元体受力模型

Fig.1   Infinitesimal of composite structure


1.2.1. 部分抗剪连接组合结构控制微分方程

对于基于Euler-Bernoulli梁理论的部分抗剪连接组合结构，根据变分法和最小势能原理推导得到控制微分方程[18-19]：

$\overline {EI} \frac{{{{\rm{d}}^4}w}}{{{\rm{d}}{x^4}}} - h\overline {EA} \frac{{{{\rm{d}}^3}{u_{\rm{s}}}}}{{{\rm{d}}{x^3}}} - q = 0\;,$
(1)

$\overline {EA} h\frac{{{{\rm{d}}^3}w}}{{{\rm{d}}{x^3}}} - \overline {EA} \frac{{{{\rm{d}}^2}{u_{\rm{s}}}}}{{{\rm{d}}{x^2}}} + {k_{\rm{s}}}{u_{\rm{s}}} = 0\;.$
(2)

式中： $\overline {EA} = ({{{E_1}{A_1} \times {E_2}{A_2}}})/({{{E_1}{A_1} + {E_2}{A_2}}})$， $EI = {E_1}{I_1}+ $ ${E_2}{I_2}$， $\overline {EI} = EI +$ $\overline {EA} {h^2}$， ${u_{\rm{s}}}$为界面滑移.

1.2.2. 部分抗剪连接组合结构挠度求解

联立控制方程式（1）、（2），消去 ${u_{\rm{s}}}$得到关于挠度 $w$的6阶微分方程：

$EI\frac{{{{\rm{d}}^6}w}}{{{\rm{d}}{x^6}}} - \overline {EI} {\alpha ^2}\frac{{{{\rm{d}}^4}w}}{{{\rm{d}}{x^4}}} = - {\alpha ^2}q + {\beta ^2}\frac{{{{\rm{d}}^2}q}}{{{\rm{d}}{x^2}}}\;.$
(3)

式中： ${\alpha ^2} = {k_{\rm{s}}}\left[{1}/{{\overline {EA} }} + {{{h^2}}}/{{\left(EI\right)}}\right]$， ${\beta ^2} = {{\overline {EI} }}/{{\left(EI\right)}}$， ${k_{\rm{s}}}$为单位长度抗剪刚度， $h$为上下两部分的形心距.

1）两端简支的部分抗剪连接组合结构在均布荷载q作用下挠度的精确解为

$\begin{split} w = & \frac{q}{{24\overline {EI} }}({x^4} - 2{x^3}l + x{l^3}) + \\ & \frac{q}{{{\alpha ^4}\overline {EI} }}({\beta ^2} - 1)[ - \tanh \;({{\alpha l}}/{2})\sinh \;(\alpha x) + \\ & \cosh \;(\alpha x) + {\alpha ^2}(lx - {x^2})/2 - 1]\;. \end{split} $
(4)

式中：l为组合结构长度.

2）两端简支的部分抗剪连接组合结构在集中荷载P作用下挠度的精确解为

$w = \left\{ \begin{aligned} & \frac{P}{{48\overline {EI} }}x(3{l^2} - 4{x^2}) + \frac{P}{{2{\alpha ^3}\overline {EI} }}({\beta ^2} - 1)\bigg[\alpha x - \\ & \qquad \frac{{\sinh \;(\alpha x)}}{{\cosh \;(\alpha l/2)}}\bigg],\;\;\;\;\;0 \leqslant x \leqslant l/2; \\ & \frac{P}{{48\overline {EI} }}(l - x)[3{l^2} - 4{(l - x)^2}] + \\ & \qquad \frac{P}{{2{\alpha ^3}\overline {EI} }}({\beta ^2} - 1)\bigg[\alpha (l - x) - \\ & \qquad \frac{{\sinh \;(\alpha l - \alpha x)}}{{\cosh \;(\alpha l/2)}}\bigg]\;,\;\;\;\;\;l/2 < x \leqslant l . \end{aligned} \right.$
(5)

2. 钢箱梁分块施工的影响参数分析

由于界面相对滑移一方面会使组合结构的整体刚度降低，另一方面会降低截面的组合效应，使组合截面的抗弯承载能力减小，而变形增大. 在钢箱梁横向分块施工中，需要找出影响部分抗剪连接箱梁块位移和应力的关键参数，分析这些参数的影响规律并加以控制，从而保证施工质量.

2.1. 影响参数归并

由均布荷载q作用下的部分抗剪连接组合结构的挠度表达式（4）可知，挠度的各影响因素表示为

$w = w(q,l,h,{A_1},{A_2},{I_1},{I_2},{k_{\rm{s}}})\;.$
(6)

上述影响参数较多，不便于方案设计. 通过对该类钢箱梁的构造特点进行分析，将相关参数进行归并，找出控制钢箱梁横向分块的最主要参数，简化分析过程，从而可以为钢箱梁桥横向分块施工提供概念上的指导. 如表1所示，对跨径L为40~90 m的典型等截面钢箱梁的构造及截面特性进行统计整理. 表中，a1、ad、i1、id分别为单位宽度顶、底板的面积和惯性矩；af、if为单位高度腹板面积和惯性矩；h1、h2分别为顶底板形心至上、下边缘的距离；m为高跨比，

表 1   常见跨径钢箱梁计算参数

Tab.1  Calculation parameters of general-span steel box girders

L/m H/m m h1/m h2/m a1/m ad/m af/m i1/m3 id/m3 if/m3
40 2.2 1/18 0.114 0.053 0.026 0.022 0.013 0.000 28 0.000 17 0.013
50 2.5 1/20 0.111 0.039 0.028 0.026 0.023 0.000 28 0.000 13 0.010
60 2.5 1/24 0.112 0.053 0.027 0.027 0.012 0.000 30 0.000 18 0.008
70 3.2 1/22 0.108 0.053 0.029 0.027 0.022 0.000 32 0.000 19 0.013
80 3.2 1/25 0.107 0.042 0.033 0.035 0.021 0.000 35 0.000 11 0.016
90 3.8 1/24 0.103 0.038 0.031 0.031 0.019 0.000 31 0.000 10 0.011

新窗口打开| 下载CSV


$m = H/L.$
(7)

由表1可知，对于给定跨径的钢箱梁，m一般可以取为1/25~1/20，因此将H与L进行归并. 由于实施分块施工的等截面单箱多室钢箱梁截面形式和局部构造基本相同，可以根据表1确定单位宽度截面参数，据此求得组合结构上、下部分截面面积A1、A2、荷载集度q、形心距h及惯性矩I1、I2为

${A_1} = {a_1}B,\;{A_2} = {a_{\rm{d}}}B + {a_{\rm{f}}}mL,$
(8)

$q = \rho ({A_1} + {A_2}),$
(9)

$h = H - {h_1} - {h_2},$
(10)

$ {I_1} = {i_1}B,\\ {I_2} = {i_{\rm{d}}}B + {i_{\rm{f}}}mL + \\ {(d - {h_2})^2}{a_{\rm{d}}}B + \frac{{{{(mL - 2d)}^2}}}{4}{a_{\rm{f}}}mL. \\ $
(11)

式中：

$d = ({{2{a_{\rm{d}}}B{h_2} + {a_{\rm{f}}}{m^2}{L^2}}})/[ {{2({a_{\rm{d}}}B + {a_{\rm{f}}}mL)}}],$

B为相邻腹板间距，ρ为钢材容重.

通过建立相应的横隔板节间模型，可以得到部分抗剪连接组合结构的抗剪刚度ks. 钢箱梁分段长度lf是由l根据实际施工取不同具体值得到. 由此可以将影响挠度的各参数归并，式（6）化简为

$w = w(L,{l_{\rm{f}}},{k_{\rm{s}}})\;.$
(12)

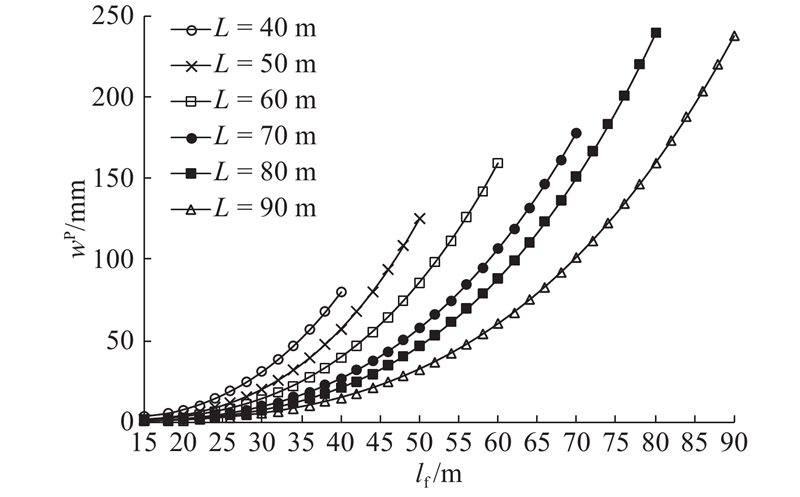
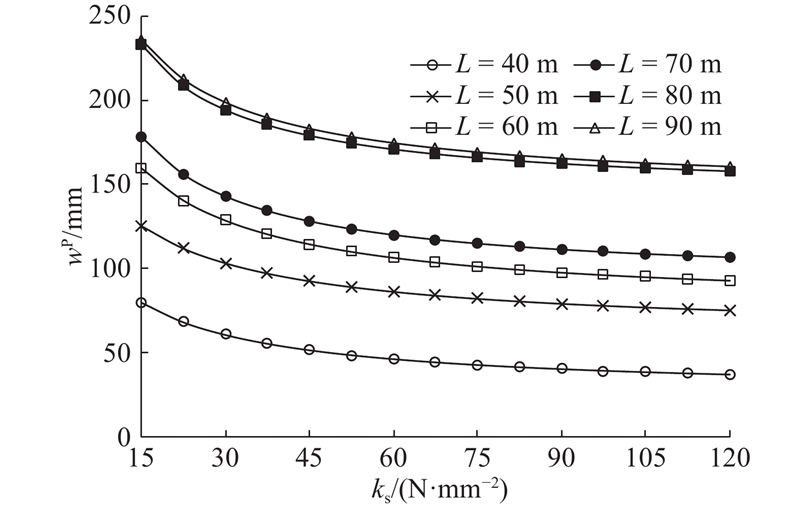
2.2. 挠度的影响参数分析

根据式(12)可知，由于L已知，w仅与lf和ks有关. 如图2、3所示分别为部分抗剪连接钢箱梁块跨中挠度随lf的变化和部分抗剪导致的挠度变化规律. 图中，wP为部分抗剪连接钢箱梁块跨中挠度，wT为完全抗剪钢箱梁块跨中挠度. 如图4所示为抗剪连接刚度对跨中挠度的影响.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   wP与lf的关系曲线

Fig.2   Relationship between wP and lf


图 3

新窗口打开| 下载原图ZIP| 生成PPT

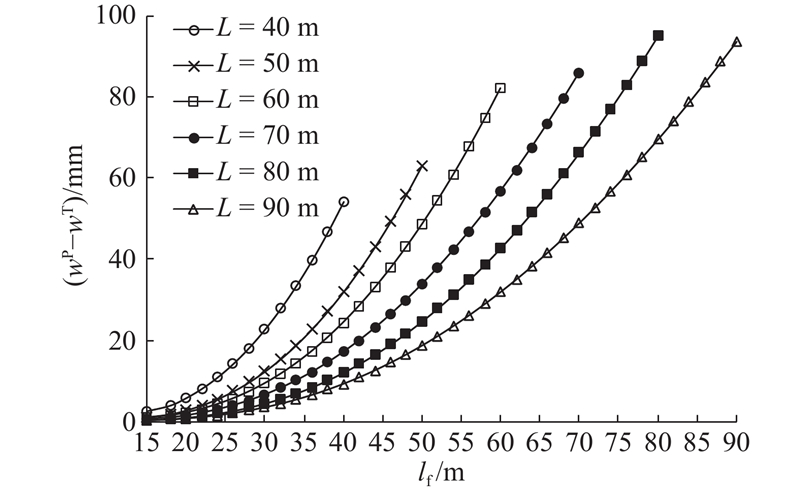
图 3   部分抗剪导致的挠度变化规律

Fig.3   Variation of deflection due to partial shear connection


图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   wP与ks的关系曲线

Fig.4   Relationship between wP and ks


从图2可以看出，随着lf的增大，wP迅速增大，且相较于大跨径钢箱梁，该效应在小跨径钢箱梁中更加明显. 当lf增大到40 m以上时，wP与wT的差值将达到55 mm，超过工程允许范围. 由图4 可知，当ks增大到50 N/mm2时，wP与wT的差值减小40%以上；当ks增大到一定程度时，逐渐趋近于完全抗剪连接钢箱梁，继续增大ks对挠度的影响很小. 当lf达到40 m时，分块施工过程中应考虑采用加固措施，以减小部分抗剪连接钢箱梁的跨中挠度. 若采用增大ks的加固措施，则应通过分析选择最优刚度，而不是盲目增大刚度.

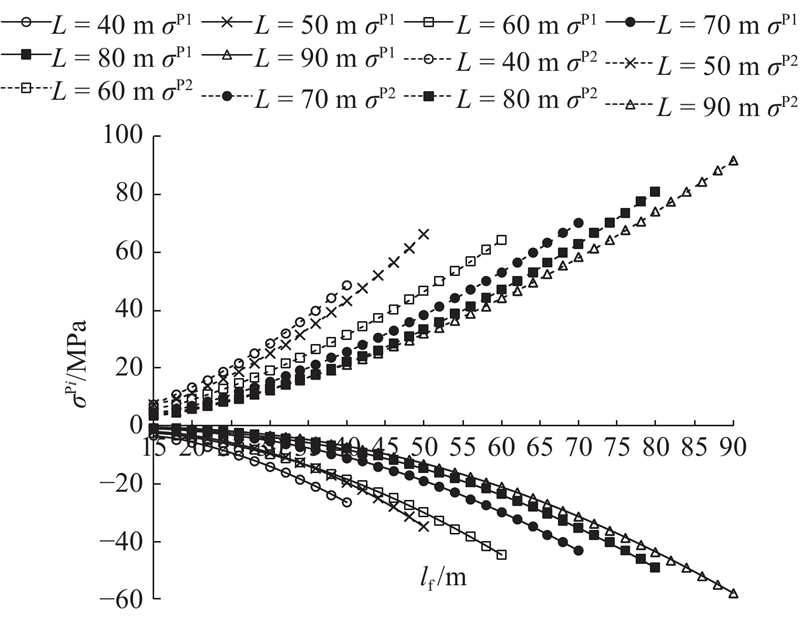
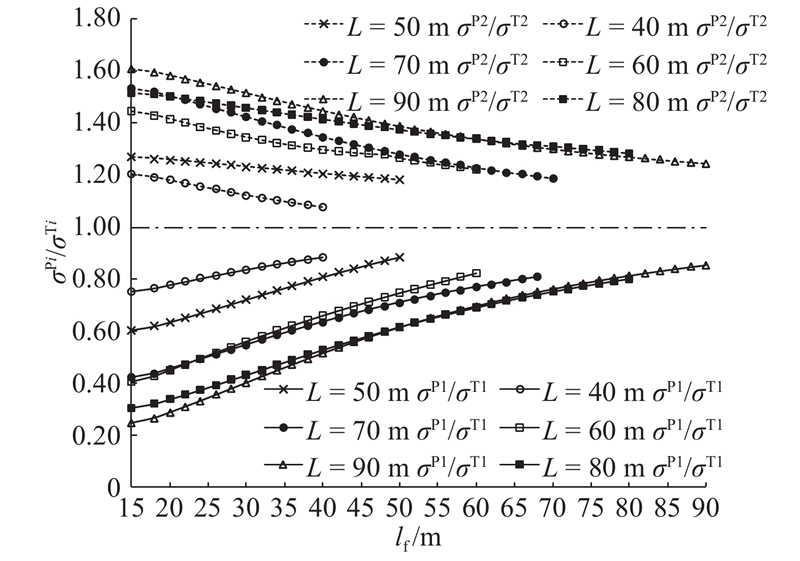
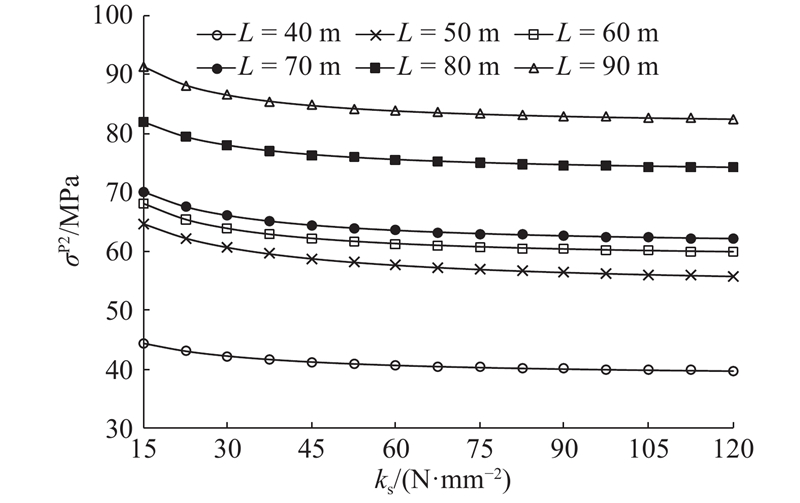
2.3. 应力的影响参数分析

在钢箱梁横向分块施工过程中，不仅要考虑是否产生过大挠度，而且要保证应力在允许范围之内. 根据1.1节的基本假设（4）可知，上、下部分曲率w〞相同，可得

$w''{\rm{ = }}\frac{{{M_1}}}{{{M_2}}} = \frac{{E{I_1}}}{{E{I_2}}} = \frac{{M - Nh}}{{EI}}\;.$
(13)

部分抗剪连接组合结构上、下缘应力σPi（i=1,2）为

${\sigma ^{{\rm{P}}i}} = {N}/{{{A_i}}} + {{{M_i}{h_i}}}/{{{I_i}}}\;.$
(14)

如图5、6所示分别为σPi与lf的关系和部分抗剪导致的应力变化规律. 图中，σTi（i=1，2）为完全抗剪连接钢箱梁的上、下缘应力. 如图7所示为ks对σP2的影响.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   σPi与lf的关系曲线

Fig.5   Relationship between σPi and lf


图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   部分抗剪导致的应力变化规律

Fig.6   Variation of stress due to partial shear connection


图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   σP2与ks的关系曲线

Fig.7   Relationship between σP2 and ks


由图5可知，当lf不超过30 m时，σPi最大不超过25 MPa，对吊装施工的影响较小. 当吊装节段较长时，如大跨桥梁整孔吊装，σPi超过80 MPa，在施工过程中必须考虑部分抗剪对应力的影响. 图6显示滑移造成的σP1小于σT1，滑移对上缘应力的影响可以忽略；σP2大于σT2，下缘受力更不利. 由图7可知，随着ks的增大，σP2虽然逐渐减小，但相对于挠度而言，部分抗剪效应对应力的影响不是特别明显.

综上所述，lf对横向分块施工钢箱梁跨中挠度的影响显著，因此在实际施工中选择合适的lf很有必要. 另外，提高ks对减小挠度和应力均有一定效果，可以根据计算结果布置抗剪临时支撑来控制施工质量.

3. 分块施工技术讨论

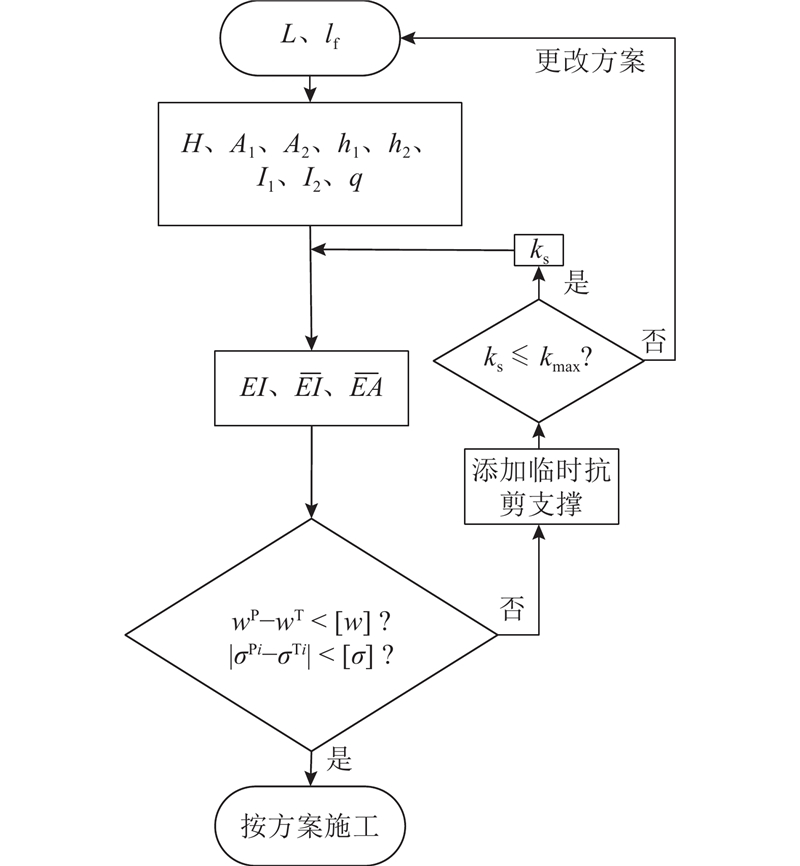
根据2.1节的讨论，可以由吊装能力、交通情况和场地空间等限制条件，先初步确定lf；由L、lf、ks以及截面参数和材料特性值计算wP和σPi，并与wT和σTi对比，将所得差值与容许值[w]和[σ]进行对比，可以据此评估分块施工对挠度和应力的影响；根据对比的结果，确定分块方案的可行性. 若吊装梁块的挠度和应力超过上述控制指标，则需要考虑通过设置临时抗剪撑或施加跨中顶升力来改善变形和受力特性；特别是当ks增大到抗剪临时撑所能提供的最大值kmax时，挠度和应力仍无法控制在允许值之内，则应考虑更改施工方案，重新设定上述参数. 设计流程如图8所示.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   分块施工设计流程图

Fig.8   Flow chart of block construction design


4. 工程应用

近几年，杭州市因城市发展需要以及2016年G20峰会、2022年亚运会等实际交通需求，相继实施了五横四纵、秋石高架、留石快速路等工程，开展了近200公里的城市高架快速路网建设. 由于高架桥一般都是在既有主干道上建设的，施工工期基本控制在1年以内，且建设过程中不允许中断交通，采用横向分块施工的单箱多室等截面多跨连续钢箱梁得以大量运用. 下面以这些工程建设为背景，讨论单箱多室钢箱梁桥的横向分块施工效应.

4.1. 小节段钢箱梁分块施工

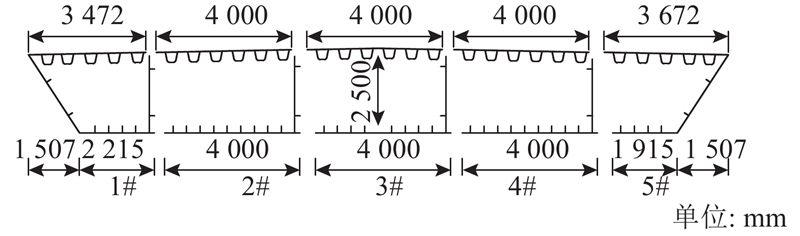
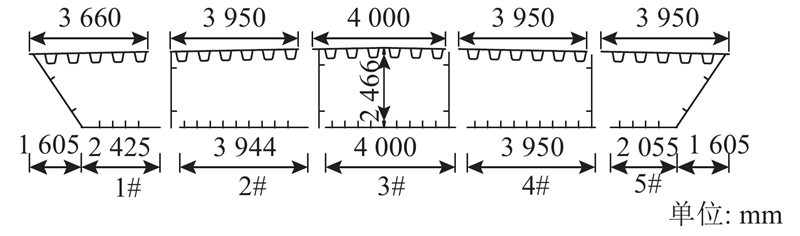
一跨径布置为（40+65+40）m的单箱五室等截面钢箱梁桥，由于受施工场地的限制，无法进行大吨位起吊，吊装时lf不宜过大，控制为27 m，横向分块形式如图9所示. 顶、底板及腹板的厚度分别为16、18和14 mm. 顶、底板及腹板加劲肋的厚度分别为8、20和12 mm，高度分别为300、200和150 mm.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   （40+65+40）m钢箱梁横向分块截面图

Fig.9   Section of（40+65+40）m steel box girder after transverse blocking


当L= 65 m，lf=27 m时，可以从图3中预测 (wP−wT)小于15 mm，即不超过[w]，不需要采用加固措施. 分块后节段的挠度结果如图10所示，(wP−wT)为9 mm，与预测值相符. 由于lf较小，吊装节段wP最大仅为12.2 mm. 由2.3节的讨论可知，σP2较σP1更不利，σP2理论及实测结果如图11所示. σP2最大值为12.9 MPa，|σP2−σT2|最大为1.5 MPa，在工程允许范围内. 综合考虑分块节段的挠度与应力影响，可以直接吊装而无需额外采用加固措施，如图12所示. 施工过程中的变形和应力实测值与理论值对比显示，两者吻合较好.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

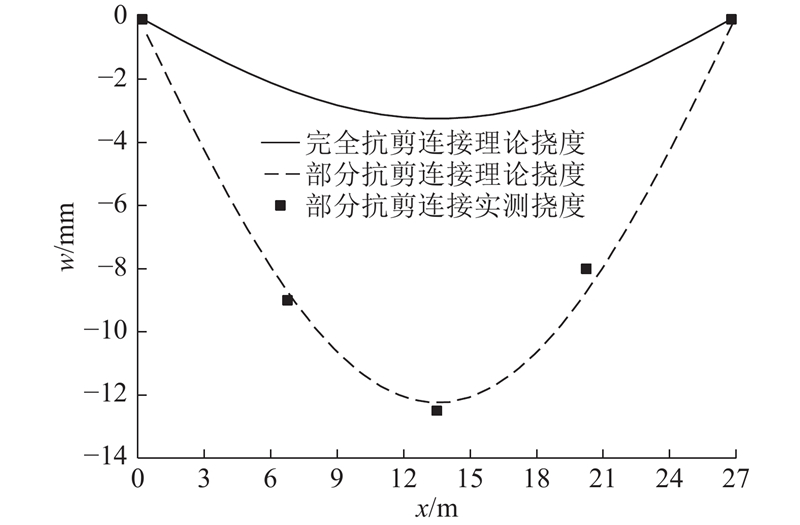
图 10   27 m吊装段挠度理论值与实测值的对比

Fig.10   Comparison of theoretical deflection result and practical data of 27 m hoisting segment


图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   27 m吊装段底板应力理论值与实测值的对比

Fig.11   Comparison of theoretical stress result and practical data of 27 m hoisting segment


图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   横向分块施工现场吊装图

Fig.12   Field hoisting of transverse block construction


4.2. 基于抗剪支撑的大节段钢箱梁分块施工

一跨径布置为（40+60+40）m单箱五室等截面钢箱梁桥，为了保证桥城市主干道的交通不受影响，要求施工期通行净空不小于35 m，施工时lf最大为38 m，横向分为5块. 如图13所示，顶、底板及腹板的厚度分别为16、20和12 mm. 顶、底板及腹板加劲肋的厚度分别为8、6和10 mm，高度分别为280、260和140 mm.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   （40+60+40）m钢箱梁横向分块截面图

Fig.13   Section of（40+60+40）m steel box girder after transverse blocking


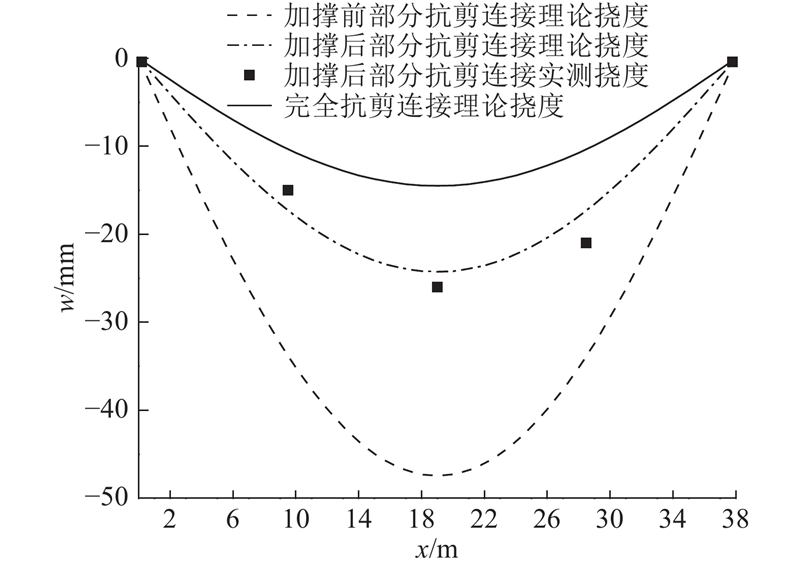
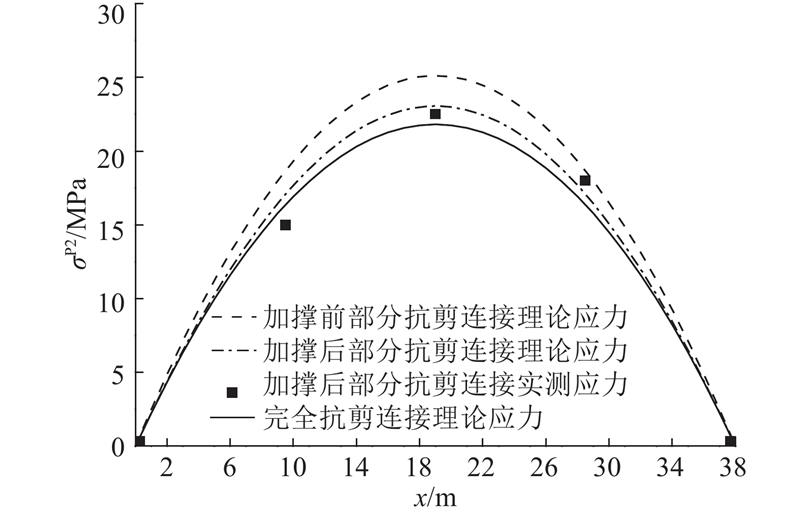
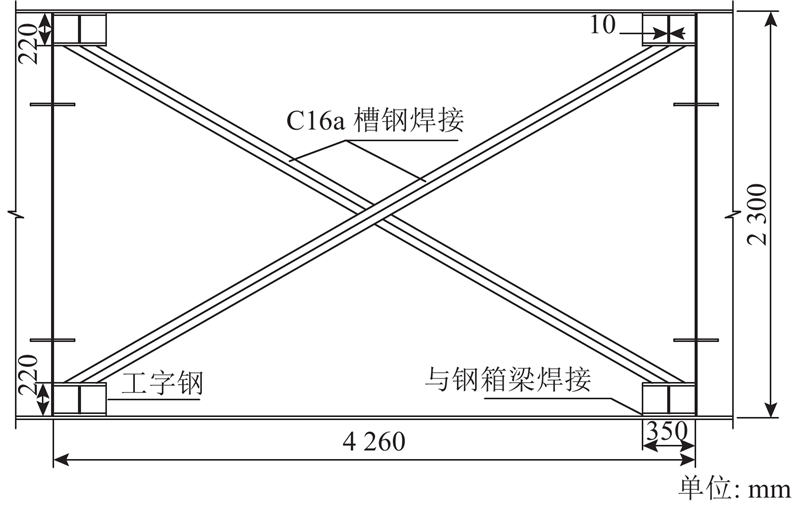
当L=65 m，lf=38 m时，由图3可以预测(wP−wT)达到25 mm，需要采用加固措施. 分块后节段挠度和应力的理论和实测结果如图14、15所示. 在没有任何加固措施时，wP为46 mm，(wP−wT)为31 mm，与预测值相符并且超过允许值. σP2的最大值为25.2 MPa，在工程允许范围内，应力增大效应不明显. 由于分块后的箱梁块端部滑移明显，可以在端部设置抗剪临时撑来改善受力变形特性，如图16所示. X型抗剪临时撑的构造及连接方式如图17所示. 通过抗剪支撑加固，增大了部分抗剪连接钢箱梁的ks，可以利用两端简支的部分抗剪连接组合结构在均布荷载q作用下的挠度计算公式（4），通过改变ks来计算加固后分块钢箱梁的挠度，并结合式（13）、（14）计算应力. 支撑后σP2略有减小，而wP=24 mm，减小47.8%，可见抗剪临时支撑对减小挠度的效果十分明显.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   38 m吊装段挠度理论与实测值对比

Fig.14   Comparison of theoretical deflection result and practical data of 38 m hoisting segment


图 15

新窗口打开| 下载原图ZIP| 生成PPT

图 15   38 m吊装段底板应力理论与实测值对比

Fig.15   Comparison of theoretical stress result and practical data of 38 m hoisting segment


图 16

新窗口打开| 下载原图ZIP| 生成PPT

图 16   抗剪临时支撑加固钢箱梁块

Fig.16   Block of steel box girder strengthened by X-type brace


图 17

新窗口打开| 下载原图ZIP| 生成PPT

图 17   X型抗剪临时支撑构造图

Fig.17   Structural map of X-type brace


4.3. 基于临时支点的大节段钢箱梁分块施工

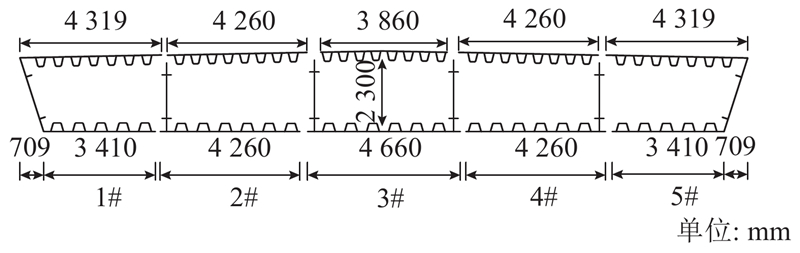
一跨径布置为（55+65）m单箱五室等截面钢箱梁桥，为了加快施工进度并确保结构线形，考虑到吊装能力，箱梁沿横向分为5块，吊装时lf最大为55 m. 横向分块如图18所示，顶、底板及腹板的厚度分别为20、25和16 mm. 顶、底板及腹板加劲肋的厚度分别为8、12和14 mm，高度分别为300、200和150 mm.

图 18

新窗口打开| 下载原图ZIP| 生成PPT

图 18   （55+65）m钢箱梁横向分块截面图

Fig.18   Section of (55+65) m steel box girder after transverse blocking


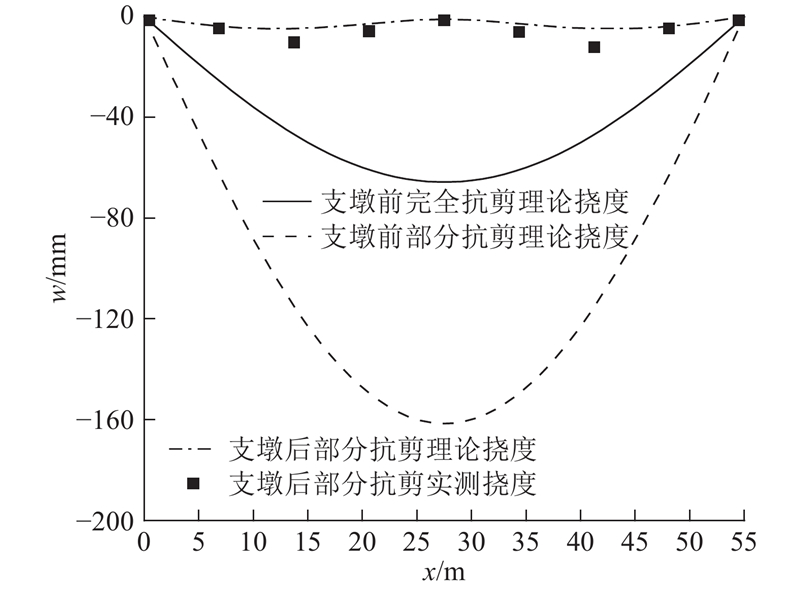
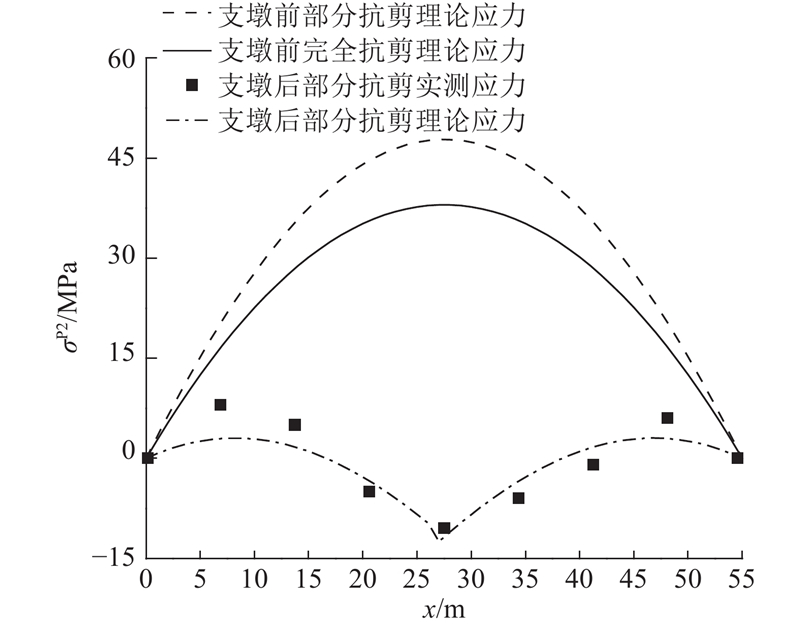
当L=65m，lf=55m时，由图3可以确定(wP−wT)将超过[w]，预测需要采用加固措施. 分块后节段挠度和应力的理论和实测结果如图19、20所示. 理论分析表明，横向分块后wP达到144.0 mm，(wP−wT)为78.4 mm，远超工程允许范围. σP2的最大值为47.8 MPa，与完全抗剪连接相比，|σP2−σT2|最大为9.8 MPa，未超出工程允许范围，应力增大效应不明显. 由于部分抗剪连接引起的挠度过大，采用在跨中设置临时支点的方法，如图21所示. 跨中临时支墩加固相当于作用一个竖向集中力，可以由式（4）、（5）计算挠度，根据叠加原理和临时支墩处挠度为零解得竖向集中力，进而得到边跨各截面挠度，结合式（13）、（14）计算应力. 结果表明，在跨中临时墩处会产生压应力，但较小；整体挠度的减小效果十分明显，满足施工线形要求，且与实测值吻合良好.

图 19

新窗口打开| 下载原图ZIP| 生成PPT

图 19   55 m吊装段挠度理论与实测值对比

Fig.19   Comparison of theoretical deflection result and practical data of 55 m hoisting segment


图 20

新窗口打开| 下载原图ZIP| 生成PPT

图 20   55 m吊装段底板应力理论与实测值对比

Fig.20   Comparison of theoretical stress result and practical data of 55 m hoisting segment


图 21

新窗口打开| 下载原图ZIP| 生成PPT

图 21   跨中临时支墩支撑

Fig.21   Supported by mid-span temporary pier


5. 结　论

（1）根据部分抗剪连接组合结构的分析理论，考虑实际工程的设计特点和变形规律，对影响钢箱梁横向分块施工效应的参数进行归并，建立分块施工结构形状尺寸参数与结构挠度之间的关系式，分析影响规律，为横向分块施工提供了理论支撑.

（2）对横向分块施工技术进行探讨，给出施工方法的设计流程，并将该方法应用于实例工程，解决了多座不同跨径城市高架钢箱梁桥的快速施工问题，可以为同类工程提供参考.

参考文献

陈建华

城市高架桥结构方案关键因素分析及发展构想

[J]. 桥梁建设, 2013, 43 (4): 99- 104

[本文引用: 1]

CHEN Jian-hua

Critical factor analysis and development conceiving of structural schemes for urban viaducts

[J]. Bridge Construction, 2013, 43 (4): 99- 104

[本文引用: 1]

宫禄尧, 杨培娜, 邱唐虎

复杂交通状况下大跨立交桥钢箱梁施工关键技术

[J]. 世界桥梁, 2015, 43 (1): 23- 26

[本文引用: 1]

GONG Lu-yao, YANG Pei-na, QIU Tang-hu

Construction techniques for long span overpass steel box girder under the complex traffic condition

[J]. World Bridges, 2015, 43 (1): 23- 26

[本文引用: 1]

KIM T H

Comparison of totally prefabricated bridge substructure designed according to Korea highway bridge design (KHBD) and AASHTO-LRFD

[J]. International Journal of Concrete Structures and Materials, 2013, 7 (4): 319- 332

DOI:10.1007/s40069-013-0050-3      [本文引用: 1]

汪劲丰, 张良, 向华伟, 等

城市钢箱梁桥横向分块施工分析

[J]. 桥梁建设, 2017, 47 (1): 109- 113

WANG Jin-feng, ZHANG Liang, XIANG Hua-wei, et al

Analysis of construction of an urban steel box girder bridge in blocks in transverse direction

[J]. Bridge Construction, 2017, 47 (1): 109- 113

胡永生

公铁合建段公路大跨度钢箱梁施工技术

[J]. 桥梁建设, 2014, 44 (2): 96- 100

[本文引用: 1]

HU Yong-sheng

Construction techniques for long span roadway steel box girders of rail-cum-road section of Tongling Changjiang River Bridge

[J]. Bridge Construction, 2014, 44 (2): 96- 100

[本文引用: 1]

王凌波, 刘鹏, 李源, 等

宽幅钢箱梁斜拉桥悬拼匹配技术研究

[J]. 中国公路学报, 2016, 29 (12): 102- 108

DOI:10.3969/j.issn.1001-7372.2016.12.013      [本文引用: 1]

WANG Ling-bo, LIU Peng, LI Yuan, et al

Research on matching technology in cantilever erection for wide steel box of cable-stayed bridge

[J]. China Journal of Highway and Transport, 2016, 29 (12): 102- 108

DOI:10.3969/j.issn.1001-7372.2016.12.013      [本文引用: 1]

张玉平, 袁鹏, 罗超云, 等

嘉绍大桥钢箱梁施工过程中局部稳定及强度分析

[J]. 公路交通科技, 2014, 31 (2): 47- 53

DOI:10.3969/j.issn.1002-0268.2014.02.009      [本文引用: 1]

ZHANG Yu-ping, YUAN Peng, LUO Chao-yun, et al

Analysis on local stability and strength of steel box girder in construction process of Jiaxing-Shaoxing Bridge

[J]. Journal of Highway and Transportation Research and Development, 2014, 31 (2): 47- 53

DOI:10.3969/j.issn.1002-0268.2014.02.009      [本文引用: 1]

BIEZMA M V, SCHANACK F

Collapse of steel bridges

[J]. Journal of Performance of Constructed Facilities, 2007, 21 (5): 398- 405

DOI:10.1061/(ASCE)0887-3828(2007)21:5(398)      [本文引用: 1]

BRADY S

West gate bridge collapse: the story of the box girders

[J]. Structural Engineer Journal of the Institution of Structural Engineer, 2016, 94 (10): 26- 28

[本文引用: 1]

蒋丽忠, 余志武, 李佳

均布荷载作用下钢-混凝土组合梁滑移及变形的理论计算

[J]. 工程力学, 2003, 20 (2): 133- 137

DOI:10.3969/j.issn.1000-4750.2003.02.025      [本文引用: 1]

JIANG Li-zhong, YU Zhi-wu, LI Jia

Theoretical analysis of slip and deformation of steel-concrete composite beam under uniformly distributed loads

[J]. Engineering Mechanics, 2003, 20 (2): 133- 137

DOI:10.3969/j.issn.1000-4750.2003.02.025      [本文引用: 1]

刘寒冰, 马辉, 刘天明, 等

竖向集中荷载作用下钢-混凝土组合梁的解析解

[J]. 中国公路学报, 2010, 23 (4): 39- 44

DOI:10.3969/j.issn.1001-7372.2010.04.007      [本文引用: 1]

LIU Han-bing, MA Hui, LIU Tian-ming, et al

Analytical solution of steel-concrete composite beam under vertical loads

[J]. China Journal of Highway and Transport, 2010, 23 (4): 39- 44

DOI:10.3969/j.issn.1001-7372.2010.04.007      [本文引用: 1]

苗林, 陈德伟

考虑层间滑移效应的组合梁解析计算

[J]. 同济大学学报: 自然科学版, 2011, 39 (8): 1113- 1119

[本文引用: 1]

MIAO Lin, CHEN De-wei

Closed-form solution of composite beam considering interfacial slip effects

[J]. Journal of Tongji University: Natural Science, 2011, 39 (8): 1113- 1119

[本文引用: 1]

XU R, WU Y F

Two-dimensional analytical solutions of simply supported composite beams with interlayer slips

[J]. International Journal of Solids and Structures, 2007, 44 (1): 165- 175

DOI:10.1016/j.ijsolstr.2006.04.027      [本文引用: 1]

XU R, WU Y F

Free vibration and buckling of composite beams with interlayer slip by two-dimensional theory

[J]. Journal of Sound and Vibration, 2008, 313 (3-5): 875- 890

DOI:10.1016/j.jsv.2007.12.029     

XU R, WU Y F

Static, dynamic, and buckling analysis of partial interaction composite members using Timoshenko's beam theory

[J]. International Journal of Mechanical Sciences, 2007, 49 (10): 1139- 1155

DOI:10.1016/j.ijmecsci.2007.02.006      [本文引用: 1]

ZONA A, RANZI G

Shear connection slip demand in composite steel-concrete beams with solid slabs

[J]. Journal of Constructional Steel Research, 2014, 102 (11): 266- 281

[本文引用: 1]

邹杨, 周志祥, 唐亮

考虑滑移效应组合梁弯曲应力和界面剪力分析

[J]. 工程力学, 2013, 30 (11): 173- 179

[本文引用: 1]

ZOU Yang, ZHOU Zhi-xiang, TANG Liang

Analysis of flexural stresses and interface shear force of composite beams considering slip effect

[J]. Engineering Mechanics, 2013, 30 (11): 173- 179

[本文引用: 1]

XU R, CHEN D

Variational principles of partial-Interaction composite beams

[J]. Journal of Engineering Mechanics, 2012, 138 (5): 542- 551

DOI:10.1061/(ASCE)EM.1943-7889.0000364      [本文引用: 1]

徐荣桥, 陈德权

组合梁挠度计算的改进折减刚度法

[J]. 工程力学, 2013, 30 (2): 285- 291

[本文引用: 1]

XU Rong-qiao, CHEN De-quan

Modified reduced stiffness method for calculating the deflection of composite beams

[J]. Engineering Mechanics, 2013, 30 (2): 285- 291

[本文引用: 1]

/

〈 〉