在这样一个信息爆炸的时代,Web上的信息无时无刻不在飞速增长,用户在面对大量的信息时很难快速、准确地找到理想的信息. 通常,只有少部分的商品被众人选择,大量的商品不会被注意. 在很多情况下,用户浏览网页或查找信息时,其中的大部分内容对用户来讲都是无用且不必要的,用户必须花费很多精力仔细浏览来获取所需信息. 推荐系统的诞生不但可以使用户更快、更准确地找到自己真正喜欢或有用的信息,给用户带来了良好的体验,而且为商人带来极大的便利,给他们的信息与商品带来了推广,因此在现实应用场景中,推荐系统的表现十分优秀. 在众多推荐技术中,由Goldberg等提出的协同过滤推荐算法(collaborative filtering recommendation algorithm,CF算法)精度高,应用范围广,成果显著[1].
由于传统的协同过滤技术对于稀疏的评分矩阵处理效果不好[4],许多国内外的专家都针对CF算法中评分矩阵的稀疏性问题提出改进. 其中矩阵分解技术是较常用的方案之一,非负矩阵分解(NMF)具有容易解释、算法相对简单等优点,在解决稀疏性问题上有良好的表现.
研究表明,Slope One 算法在比较稠密的数据集下,推荐效果较好,但在比较稀疏的数据集下推荐效果很差[5],基于矩阵分解的方法在抗稀疏性方面很有效,因此将非负矩阵分解引入到Slope One算法中,提出基于非负矩阵分解的Slope One算法.
1. 相关工作
1.1. Slope One算法简介
1.1.1. Slope One算法原理
Slope One算法的基本原理是一个非常简洁的一元方程
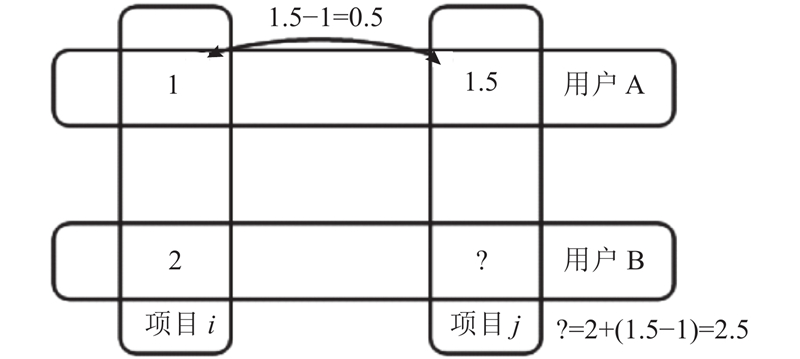
图 1
根据Slope One算法,计算用户B对项目j的评分为:2+(1.5−1)=2.5.
定义项目i相对于项目j的平均偏差计算公式:
式中:Sj,i为同时对项目i与项目j进行过评分的用户集合,ui和uj分别为用户对项目i和项目j的评分,card为集合中的元素数量.
在以上定义的基础上,能够使用devj,i+ui来计算用户u对项目j的预测值. 将全部这种可能的预测值取平均,可得
式中:Rj表示用户u进行过评分且满足条件(i≠j且Sj,i非空)的所有项目集合.
对于足够稠密的数据集,可以使用近似:
式中:S(u)为用户u评过分的所有项目集合.
将式(3)简化为
1.1.2. Weighed Slope One算法
Slope One算法在计算项目i相对于项目j的平均偏差devj,i的过程中,未考虑不同用户间的可信度差异[8]. 若有1 000名用户都对项目k与项目j进行过评价,但仅有10名用户都对项目i与项目j完成过评价,计算得到的devj,k比devj,i更具有说服力.
其中的一个修正是对最终的平均使用加权,即Weighted Slope One[9],预测公式如下:
式中:cj,i=card(Sj,i(x)),devj,i为项目i与项目j评分的平均偏差,ui为用户u对项目i的评分.
Weighted Slope One在原有Slope One算法的基础上,考虑到每一个项目(商品)对目标项目的影响,使算法推荐更加准确. Weighted Slope One存在不足,该算法仅考虑不同项目的评分偏差,忽略不同用户存在的相似性,带来了新的误差. Lemire教授提出Bi-Polar Slope One算法[10],考虑到了不同用户的相似性.
1.1.3. Bi-Polar Slope One算法
Bi-Polar Slope One算法在Weighted Slope One的基础上,将用户进行过评分的项目区分为like与dislike 2种. 如果用户u对项目i的评分ui比该用户对所有项目的平均评分大,则用户u喜欢项目i,否则用户不喜欢项目i:
式中:
类似地,可以定义对项目i与项目j具有相同喜好的用户集合:
根据以上定义,能够通过下式得出新的偏差:
于是,可以从项目i计算得到预测值:
Bi-Polar Slope One的预测公式如下:
Bi-Polar Slope One在Weighted Slope One的基础上加入用户间的相似性的判断,提升了精确度. 只粗略地根据用户对项目的平均评分来区分like与dislike,会引起误差,不能满足推荐需要.
1.2. 非负矩阵分解算法简介
Lee等[11]首次公布了非负矩阵分解算法(NMF). NMF解决了许多常规矩阵分解技术中存在的问题,在当时引起了世界上许多研究人员的讨论与深入研究.
NMF的基本思想是将数据非负的矩阵R分解为低维的非负矩阵P、Q,满足R≈PQ,其中R为原始矩阵,P为基矩阵,Q为系数矩阵. 在原始的非负矩阵R中,每个列向量为矩阵P的全部行向量的加权和,权重系数为Q中相对应的列向量的元素. 假设对m个n维空间的样本进行相应的数据处理,m×n的原始矩阵R,m×k的基矩阵P与k×n的系数矩阵Q,这样一组基向量构造出了k维,Q中的每一列都可以大略地看作原始矩阵R对应的列向量对于k维空间的投影[12].
在推荐系统中,在R上完成预处理操作,变换成非负矩阵,算法步骤如下.
表 3
Tab.3
| 输入:原有的用户-项目评分矩阵R(m×n),ks为特征属性个数,steps为迭代次数,a=0.000 2为梯度下降常数,b=0.02用来控制用户特征向量和条目特征向量的比例,用来进行规范化,防止过拟合. |
| 输出:较稠密的用户-项目评分矩阵Rnew(m×n) |
| 1 for step<steps//迭代次数 |
| 2 for i<len(R) |
| 3 for j<len(R[i]) |
| 4 if R[i,j]>0//用户给出了评分 |
| 5 eij=R[i,j]−P[i,j]·Q[i,j] |
| 6 for k<ks |
| 7 P[i][k]=P[i][k]+a(2eij ·Q[k][j]−b·P[i][k]) |
| 8 Q[k][j]=Q[k][j]+a(2eij ·P[i][k]−b·Q[k][j]) |
| 9 end for |
| 10 end if |
| 11 end for |
| 12 end for |
| 13 式(7) |
| 14 end for |
| 15 sreturn Rnew(m×n) |
2. 基于非负矩阵分解的Slope One算法
由1.2节可知,进行非负矩阵分解后的矩阵P、Q的乘积,即原有矩阵的近似矩阵是一个m×n的矩阵. 若将近似矩阵的每一行看作该行所对应的用户的特征,则选择Pearson系数完成相似性的计算,可得m×m的用户相似度矩阵Spearson,其中Spearson(i,j)为用户i与用户j之间的相似度.
式中:
在上述数据模型和设计思想的基础上,归纳NMF-Slope One算法的输入、输出及步骤如下.
表 4
Tab.4
| 输入:较稀疏的用户-项目矩阵 R(m×n);目标用户 u,目标项目 i,ks 为特征属性个数,steps 为迭代次数,a=0.000 2 为梯度下降常数,b=0.02 用来控制用户特征向量和条目特征向量的比例,用来进行规范化,防止过拟合. |
| 输出:u对itemi的预测评分pu,i |
| 1 for step<steps//迭代次数 |
| 2 for i<len(R) |
| 3 for j<len(R[i]) |
| 4 if R[i,j]>0//用户给定评分 |
| 5 eij=R[i,j]−P[i,j]·Q[i,j] |
| 6 for k<ks |
| 7 P[i][k]=P[i][k]+a(2eijQ[k][j]−bP[i][k]) |
| 8 Q[k][j]=Q[k][j]+a(2eijP[i][k]−bQ[k][j]) |
| 9 end for |
| 10 end if |
| 11 end for |
| 12 end for |
| 13 式(7) |
| 14 end for |
| 15 根据式(8)构建不同用户的相似度矩阵 |
| 16 Nu ← TopK(u) |
| 17 N=|Nu| |
| 18 |
| 19 |
3. 实验结果及其分析
3.1. 实验所用数据集和实验选择的度量标准
使用的数据集来自MovieLens网站(http://movielens.umn.edu)[15]. 该网站是由美国Minnersota大学GroupLens研究小组所建立与维护的一个非赢利、以研究为宗旨的实验性网站. 每天均有数以百计的用户浏览MovieLens网站,参与到电影的评分或接受网站的推荐.
在MovieLens上的数据集中,随机选取943名使用者对1 682部影片参与的100 000评分数据信息. 其中,使用者对影片的打分为(1,2,3,4,5)的离散型整数,越接近5表示用户对影片的评价越好,即对该影片的喜好程度越高.
为了衡量推荐算法的优劣,通过选取MAE(预测到用户评分和真实评分的平均误差)、RMSE(均方根误差)2个值来完成定量分析. 若采用NMF-Slope One算法预测出的用户评分为{p1,p2,p3,…,pn},用户的真实评分为{q1,q2,q3,…,qn},则MAE与RMSE的计算公式如下:
3.2. 实验结果及分析
图 2
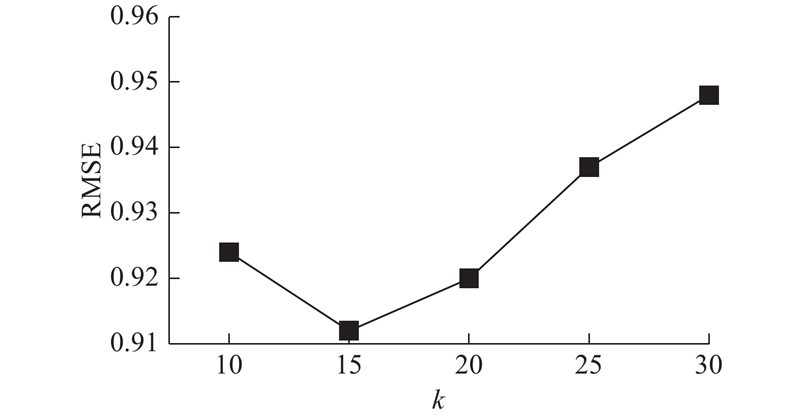
图 3
由图3可知,当k=15时,NMF-Slope One算法的RMSE与MAE最小. 其中,RMSE=0.912 6,MAE=0.762 4,即当k=15时,NMF-Slope One算法的推荐效果最佳.
3.2.1. NMF-Slope One算法与传统Slope One算法的比较
将相似度阈值设为0.2,在k=15的条件下进行实验,比较NMF-Slope One算法、Weighted Slope One算法与Bi-Polar Slope One算法的推荐效果. 实验结果如表1所示.
表 1 不同Slope One算法的RMSE与MAE
Tab.1
| 算法 | RMSE | MAE |
| Bi-Polar Slope One | 1.08 | 1.06 |
| Weighted Slope One | 0.98 | 0.97 |
| NMF-Slope One | 0.92 | 0.92 |
从表1的实验结果可知,NMF-Slope One比传统的Weighted Slope One算法与Bi-Polar Slope One算法的推荐效果更好.
3.2.2. NMF-Slope One算法与传统CF算法的比较
在相似度阈值设为0.2,k=15的条件下进行实验,比较NMF-Slope One算法、基于用户的CF算法与基于项目的CF算法的推荐效果. 实验结果如表2所示.
表 2 不同CF算法的RMSE和MAE
Tab.2
| 算法 | RMSE | MAE |
| User-Based CF | 0.97 | 0.87 |
| Item-Based CF | 1.07 | 0.92 |
| NMF-Slope One | 0.91 | 0.76 |
由表2的数据可知,NMF-Slope One算法与传统的基于用户的CF算法与基于项目的CF算法相比,效果更好.
4. 结 语
本文介绍了Slope One算法的原理,针对传统Slope One算法的不足,提出基于非负矩阵分解的Slope One改进算法. 利用该改进算法,有效解决了Slope One算法在数据较稀疏条件下的推荐效果不如传统协同过滤算法的问题. 将NMF-Slope One与Weighted Slope One、Bi-Polar Slope One算法进行比较,实验结果证明了改进后的算法有更好的推荐效果. 在数据稀疏的条件下,确定参数进行实验. 在与原始的CF算法比较后,从实验数据得出NMF-Slope One算法有较好的推荐效果.
参考文献
Comparison of collaborative filtering algorithms: Limitations of current techniques and proposals for scalable, high-performance recommender systems
[J].
QoS prediction for web services based on similarity-aware Slope One collaborative filtering
[J].
A research on the improved slope one algorithm for collaborative filtering
[J].DOI:10.1504/IJCSM.2016.077865 [本文引用: 1]
A new slope one based recommendation algorithm using virtual predictive items
[J].DOI:10.1007/s10844-017-0470-7 [本文引用: 1]
Incremental Slope-one recommenders
[J].DOI:10.1016/j.neucom.2017.07.033 [本文引用: 1]
Learning the parts of objects with non-negative matrix factorization
[J].
Multi-view clustering via multi-manifold regularized non-negative matrix factorization
[J].DOI:10.1016/j.neunet.2017.02.003 [本文引用: 1]
A Nonconvex splitting method for symmetric nonnegative matrix factorization: convergence analysis and optimality
[J].DOI:10.1109/TSP.2017.2679687 [本文引用: 1]
An oracle inequality for quasi-Bayesian nonnegative matrix factorization
[J].DOI:10.3103/S1066530717010045 [本文引用: 1]
The MovieLens datasets: history and context
[J].