基于IABC-RBF神经网络的地下水埋深预测模型

doi:10.3785/j.issn.1008-973X.2019.07.011

基于IABC-RBF神经网络的地下水埋深预测模型

邵光成^,, 章坤, 王志宇, 王小军, 卢佳

Groundwater depth prediction model based on IABC-RBF neural network

SHAO Guang-cheng^,, ZHANG Kun, WANG Zhi-yu, WANG Xiao-jun, LU Jia

收稿日期: 2018-05-17

Received: 2018-05-17

作者简介 About authors

邵光成（1975—），男，教授，从事农业水资源高效利用研究.orcid.org/0000-0001-6353-362X.E-mail:sgcln@126.com , E-mail：sgcln@126.com

摘要

为了验证基于改进人工蜂群算法的径向基函数（RBF）神经网络模型在地下水埋深预测中的可行性和优越性，在基本人工蜂群算法中引入高斯变异算子，优化初始蜜源位置，设计建立基于改进人工蜂群算法的RBF神经网络模型（IABC-RBF）. 通过输入泾惠渠灌区的年降雨量、年渠首引水量、年田间灌溉用水量、年地下水开采量和前一年的地下水埋深共5个相关影响因子的数据，对地下水埋深进行预测，与实测的地下水埋深数据进行比较，误差很小. 与RBF神经网络模型和基于基本人工蜂群算法训练的RBF神经网络模型（ABC-RBF）的预测结果进行比较，结果表明，基于改进人工蜂群算法的RBF神经网络模型收敛速度更快，预测结果误差最小，精度最高.

关键词： 人工蜂群算法 ; 径向基函数神经网络 ; 高斯变异 ; 泾惠渠灌区 ; 地下水埋深 ; 预测

Abstract

The Gaussian mutation operator was introduced into the basic artificial bee colony algorithm, and the initial nectar location was optimized in order to verify the feasibility and superiority of radial basis function (RBF) neural network model based on improved artificial bee colony algorithm in groundwater depth prediction. A RBF neural network model was designed based on improved artificial bee colony algorithm (IABC-RBF). The groundwater depth was predicted by inputting the annual rainfall, the amount of annual water intake in the first ditch, the amount of annual field irrigating, the annual groundwater exploitation and the groundwater depth in the previous year of Jinghui irrigation district. The error is very small compared with the measured groundwater depth data. The model was compared with the RBF neural network model and the RBF neural network model based on the basic artificial bee colony algorithm (ABC-RBF). Results show that the RBF neural network model based on the improved artificial bee colony algorithm has faster convergence speed, the least error of the prediction result and the highest accuracy.

Keywords： artificial bee colony algorithm ; radial basis function neural network ; Gaussian mutation ; Jinghui irrigation district ; groundwater depth ; prediction

PDF (894KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

邵光成, 章坤, 王志宇, 王小军, 卢佳. 基于IABC-RBF神经网络的地下水埋深预测模型. 浙江大学学报(工学版)[J], 2019, 53(7): 1323-1330 doi:10.3785/j.issn.1008-973X.2019.07.011

SHAO Guang-cheng, ZHANG Kun, WANG Zhi-yu, WANG Xiao-jun, LU Jia. Groundwater depth prediction model based on IABC-RBF neural network. Journal of Zhejiang University(Engineering Science)[J], 2019, 53(7): 1323-1330 doi:10.3785/j.issn.1008-973X.2019.07.011

神经网络具有非线性、自学习等特点，是处理复杂非线性问题的一种有效手段，相比于传统的统计分析模型，具有更好的实时预测性，能够解决多个自变量和因变量的问题. 常见的有小波神经网络模型^[1]、误差反向传播（back propagation，BP）神经网络模型^[2-3]、径向基函数（radial basis function，RBF）神经网络模型等^[4-6]，在地下水预测中都得到了广泛的应用.

RBF神经网络模型相较于BP神经网络模型，学习速度更快，适用性更强，已经被应用到地下水埋深预测中. 神经网络模型的输入存在多重共线性，导致网络的泛化能力较差，且求解时易陷入局部极小，收敛速度较慢，预测能力不高. 针对以上问题，可以结合优化算法来训练神经网络模型，常见的有蚁群算法^[5]、粒子群算法^[6]和遗传算法^[7]等. 人工蜂群（artificial bee colony，ABC）算法由Karaboga小组^[8]提出，受到了蜜蜂在采蜜过程中的个体分工和信息交流行为的启发. 这种模仿蜜蜂采蜜行为的算法与其他群体智能算法相比^[9]，具有全局寻优能力强、控制参数少、操作简单等优点，已被运用于资源调度^[10]、渠道断面优化^[11]、交通流预测^[12]、水质评价^[13]、电网分配^[14]等一些方面. 针对人工蜂群算法存在的易陷入局部收敛的问题，可以引入局部动态搜索算子^[15]，利用混沌扰动^[16]，动态调整局部搜索空间^[17]. 本文通过在局部搜索中引入高斯变异算子，优化了初始解空间，提出基于改进人工蜂群算法（improved artificial bee colony algorithm，IABC）的RBF神经网络模型，优化训练RBF神经网络模型的初始参数，结合了人工蜂群算法的全局搜索能力，提高了网络的学习速度，综合改善了神经网络的预测能力.

1. 基本理论

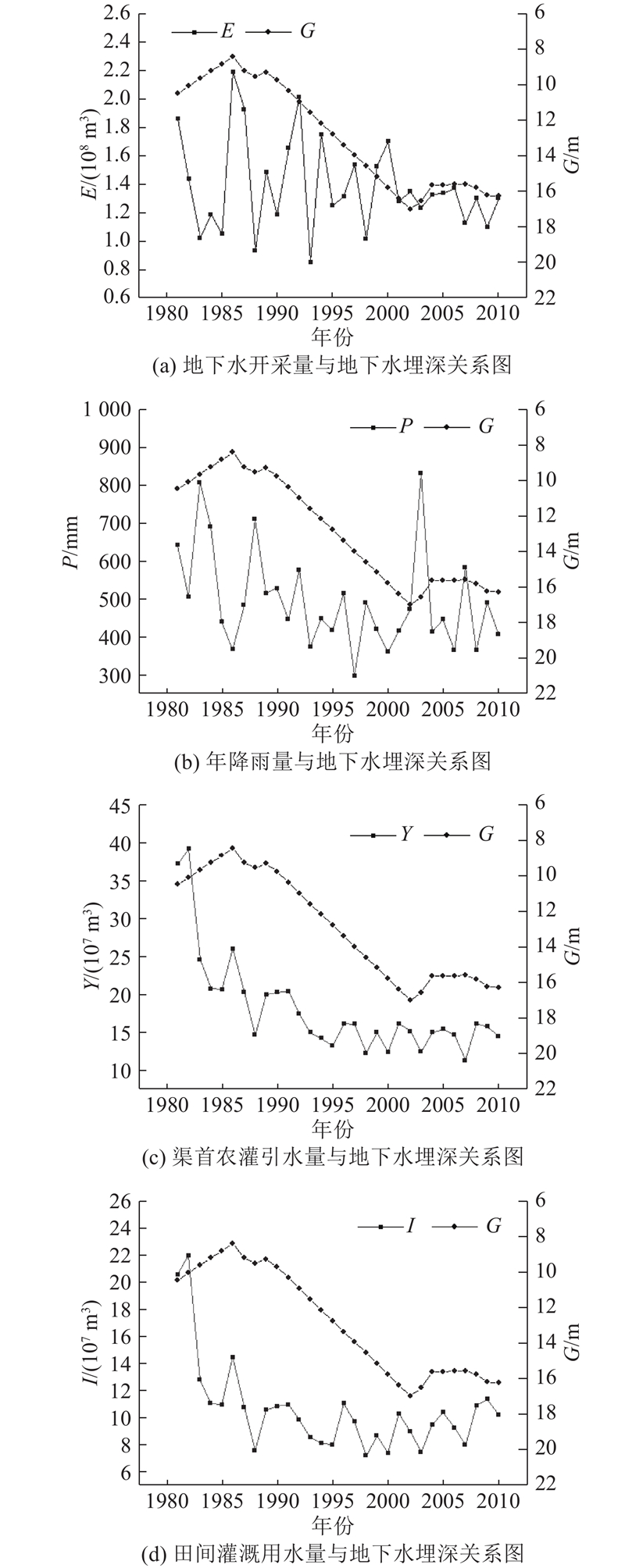
1.1. 地下水动态影响因素分析

泾惠渠灌区地处陕西省关中平原中部，是一个从泾河自流引水的渠井结合灌区. 灌区内地下水主要有潜水及承压水，承压水一般埋深约在100 m以下，不易开采. 潜水一般蓄存于第四纪全新统冲积层中，埋藏浅且易于开采，是农业用水的主要来源，各种垂向渗入为主要的补给来源，排泄方式主要是人工开采和潜水蒸发^[18]. 根据泾惠渠灌区的地形地貌特征及水文地质条件，将灌区进行分区，选取渭河漫滩及一级阶地强富水亚区作为研究区. 降雨量P、田间灌溉用水量I、渠首农灌引水量Y和地下水开采量E与研究区潜水层平均地下水埋深G的动态变化如图1所示.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1 各影响因素与地下水埋深动态关系图

Fig.1 Dynamic relationship between influence factors and groundwater depth

1.2. 基本人工蜂群算法

人工蜂群算法是一种随机搜索算法，启发于蜂群通过分工、交流和协作，通过群体智慧完成采蜜任务. 它模拟真实的蜂群采蜜过程，蜜源的位置用来代表问题的解，蜜源的花粉质量表示解的适应度. 蜂群被分为引领蜂、跟随蜂和侦察蜂3种类型，引领蜂又称雇佣蜂，数量等于跟随蜂的数量，且等于解的数目. 每个蜜源同时只有一个一个引领蜂采蜜. 引领蜂搜索蜜源并根据蜜源的情况来对蜜源进行标记，利用摇摆舞分享与蜜源质量相匹配的蜜源信息，召唤更多的蜜蜂前来开采. 跟随蜂采用随机的方式去选择开采的蜜源，同时在附近搜索新的蜜源.

一个蜜源在经过数次开采后会被弃用，对应的引领蜂将转换为侦察蜂，继续在附近寻找新的蜜源. 3类蜜蜂的作用有所区别：引领蜂用于保持解的优越性，跟随蜂可以提高收敛速度，侦察蜂则用于避免陷入局部最优^[19].

人工蜂群算法易于实现，控制参数少，稳定性强，在每次的迭代中都会进行全局搜索和局部搜索，找到最优解的概率更高，与其他群体智能算法相比收敛速度更快.

1.3. 高斯变异

高斯变异（Gaussian mutation）来源于高斯分布，高斯分布也叫正态分布. 高斯变异是在进行变异操作时用符合正态分布的一个随机数来替代原来的参数值，通过在原来状态上附加一个服从正态分布的随机向量，达到避免陷入局部最优，增加多样性，加快收敛速度的效果，提高算法的稳定性^[20].

2. 预测模型研究

2.1. 预测模型分析

在各种预测模型中，神经网络是一种模仿动物神经网络行为特征，开展分布式并行信息处理的算法数学模型. 该网络依靠系统的复杂程度，通过调整内部大量节点（或称神经元）之间相互连接的关系，从而达到处理信息的目的. 每个节点代表一种特定的输出函数，每两个节点间的连接都代表一个通过该连接信号的加权值，称为权重，这相当于人工神经网络的记忆. 网络的输出根据网络的连接方式、权重和激励函数的不同而不同. 网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达. 神经网络具有并行性、容错性和自学习性等优点，可以处理复杂的非线性多变量问题.

2.2. 预测模型建立

采用径向基函数（RBF）神经网络，是具有单隐层的3层前向网络.

1）输入层X：由信号源节点构成，仅起到数据信息的传递作用，对输入信息不作任何变换.

2）隐含层H：节点数视需要而定. 隐含层神经元核函数（作用函数）是高斯函数，对输入信息进行空间映射的变换.

3）输出层Y：对输入模式作出响应. 输出层神经元的作用函数为线性函数，对隐含层神经元输出的信息进行线性加权后输出，作为整个神经网络的输出结果.

径向基神经网络的数学模型为

(1) $ y_i = \sum\nolimits_{i = 1}^{{n_{\rm{c}}}} {{w_i}g\left( {\left\| {{{x}} - {{{c}}_i}} \right\|/{\sigma _i}} \right) + b} . $

式中：x为神经网络输入的n维向量；w_i为输出层权重；g（*）为径向基函数；c_i为径向基函数中心；σ_i为宽度；b为输出层阈值；n_c为隐含层神经元数目；||x−c_i||为向量x−c_i的范数，通常表示x与c_i间的距离.

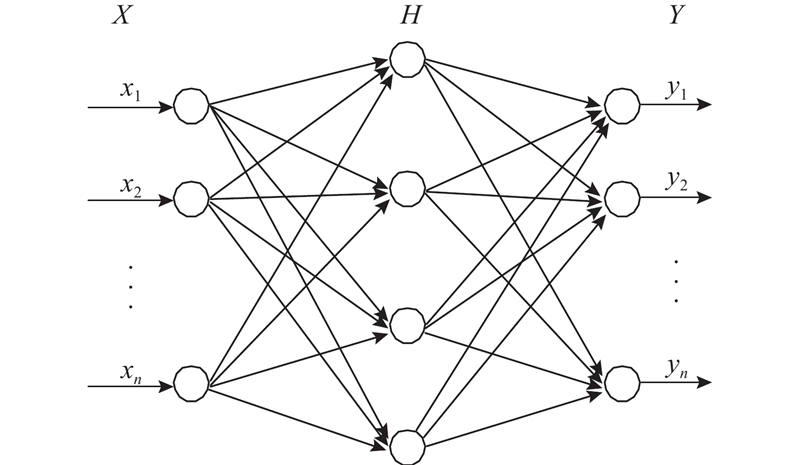
径向基神经网络的结构示意图如图2所示.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2 径向基函数（RBF）神经网络模型结构示意图

Fig.2 Schematic diagram of radial basis function (RBF) neural network model

通常选择高斯基函数为径向基函数，输出层阈值为0，该层神经元i的输出为

(2) $ {R_i}\left( {{x}} \right) = {\rm{exp}} \left[ { - {{\left\| {{{x}} - {{{c}}_i}} \right\|}^2}/\left( {2\sigma _i^2} \right)} \right]. $

若输出层单元数只有一个，则映射关系为

(3) $ y = f\left( x \right) = {{WR}} = \sum\nolimits_{i = 1}^{n_{\rm{c}}} {{w_{i}}{R_i}\left( x \right)} . $

式中：W为输出层的权值，R为隐含层神经元的输出值.

3. 模型分析及求解

3.1. 蜜源位置的初始化

首先对人工蜂群算法的参数进行初始化，维数根据需要确定的RBF神经网络参数数量确定，蜜源数即解的个数N_S，极限值limit和迭代终止次数即最大循环数，初始循环次数t=1.

随机产生某个蜜源的方法如下：

(4) $ {x_{id}} = {\rm{Unifrnd}}\left( {{M_d},{N_d},\left[ {1,D} \right]} \right). $

式中：D为解空间的维数，i取值于{ $1,\;2,\;\cdots$，N_S}，d取值于{ $1,\;2,\;\cdots$，D}，x_id表示第i个蜜源的第d个维度，M_d和N_d分别为第d个维度的下限和上限， Unifrnd函数表示产生M_d到N_d均匀分布的1×D随机数组. 通过均匀分布来优化初始蜜源位置，可以加快算法的收敛速度，在一定程度上避免陷入局部最优.

3.2. 引领蜂、跟随蜂和侦察蜂阶段

引领蜂在搜索开始阶段，寻找新蜜源的方法如下：

(5) $ {v_{id}} = {x_{id}} + \varphi \left( {{x_{id}} - {x_{jd}}} \right). $

式中：j取值于{1，2，···，N_S}，j≠i，即x_i与x_j表示2个不同的蜜源；φ为取值于[−1，1]的随机数. 采用贪婪算法，若新蜜源v_i的适应度大于x_i，则选择新蜜源v_i代替x_i，反之则保留x_i.

在引领蜂阶段结束后，引领蜂通过摇摆舞分享蜜源信息，跟随蜂根据信息，采用轮盘赌方式，按下式计算的概率进行跟随：

(6) $ {P_i} = f\left( {{{{x}}_i}} \right)/\sum\nolimits_{i = 1}^{{N_{\rm{S}}}} {f\left( {{{{x}}_i}} \right)} . $

式中：f（x_i）为第i个蜜源的适应度，

(7) $ f\left( {{{{x}}_i}} \right) = {\rm{exp}}\,\,{\left({\displaystyle{{ - {\rm{MSE}}_i}}/{{\overline {{\rm{MSE}}} }}}\right)}, $

其中MSE_i为第i个解的均方误差.

轮盘赌步骤如下:生成一个（0，1）上的随机数r，若P₁+P₂$ +\cdots+$P_i−1<r≤P₁+P₂+P₃$+\cdots+$P_i−1+P_i，则蜜源i被选中. 适应度较大的蜜源被选中的概率较大，适应度相对较小的蜜源也有被选中的可能. 跟随蜂选择蜜源跟踪开采，以保证适应度更高的蜜源开采的概率更高. 跟随蜂按式（5）在蜜源i周围找寻新蜜源，根据贪婪算法选择适应度更高的蜜源.

若一个蜜源经过数次开采没有被更新，即循环次数trial达到阈值limit，则该蜜源会被弃用，与这个蜜源对应的引领蜂角色转换为侦察蜂，根据式（4）寻找新的蜜源.

3.3. 高斯变异

对蜜源位置进行扰动，采用下式^[21]：

(8) $ {x_{id}} = {x_{id}}\left[ {1 + kN\left( {0,1} \right)} \right]. $

式中：N（0，1）为服从均值为0、方差为1的高斯分布的随机向量.

k根据下式来计算：

(9) $ k = {{\rm{exp}}\;({\displaystyle{{ - i_{\rm{t}}}}/{{{\rm{limit}}}}}}). $

式中：i_t为当前迭代次数.

若新密源的适应度比旧蜜源大，则取代旧蜜源，反之保留旧蜜源.

在训练达到终止条件后，输出最优蜜源.

3.4. 模型建立

初始化RBF神经网络模型，建立蜜源位置与RBF神经网络模型的训练精度Goal、扩散常数Spread和最大神经元数目MN之间的映射，蜜源初始位置表示参数初始解.

将输出的最优蜜源对应的参数值作为RBF神经网络模型的参数，然后进行训练，直至满足条件为止.

基于高斯变异的人工蜂群算法优化训练过程如图3所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3 改进人工蜂群算法优化过程图

Fig.3 Optimization process diagram of improved artificial bee colony algorithm

4. 算例分析

4.1. 数据来源

根据泾惠渠灌区地形地貌特征及其水文地质条件，将灌区进行分区，选取灌区西南部的渭河漫滩及一级阶地强富水亚区作为研究区，分区面积为43 km²，占灌区总面积为3.68%. 数据来自研究区内观测井1981—2010年的地下水动态观测值^[22]，取观测值的算术平均值作为研究区的平均地下水埋深G，将年降雨量P、年渠首农灌引水量Y、年田间灌溉用水量I、年地下水开采量E和前一年的地下水埋深作为影响因子. 由于研究区的地下水埋深已超过极限蒸发深度7 m，年蒸发量不作为影响因子. 将1981—2005年作为训练数据，2006—2010年作为预测数据，在训练和预测之前先进行归一化处理.

4.2. 模型建立结果

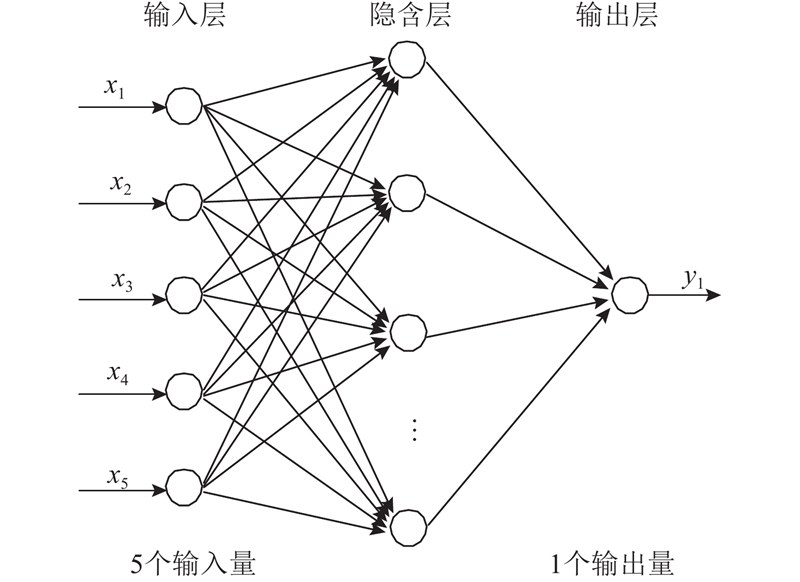
确定的RBF神经网络模型的输入层神经元数目为5，对应于5个影响因子；输出层神经元为1，对应于输出的地下水埋深. 通过MATLAB工具箱newrb函数，建立3层RBF神经网络模型. 结构如图4所示.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4 RBF神经网络模型结构示意图

Fig.4 Schematic diagram of RBF neural network model

在人工蜂群算法的优化训练过程中，蜂群的种群规模为20，最大循环次数为50，阈值limit的取值依赖于种群规模和解的维度，将limit的值定为两者的乘积再乘以0.6.

通过改进的人工蜂群算法优化训练RBF神经网络模型，将程序独立运行10次，每次运行之后的参数优化结果如表1所示.

表 1 RBF神经网络模型参数训练结果

Tab.1 Parameter training results of RBF neural network model

序号	参数
序号	Goal	Spread	MN
1	0.000 862	1.826 070	8
2	0.000 498	2.933 067	10
3	0.000 798	1.688 562	12
4	0.000 789	1.825 936	12
5	0.000 254	1.326 492	11
6	0.000 467	2.526 777	14
7	0.000 207	1.522 293	9
8	0.000 309	1.318 309	8
9	0.000 763	1.383 367	7
10	0.000 168	2.421 241	8

新窗口打开| 下载CSV

在训练精度Goal、扩散常数Spread和最大神经元数目MN 3个参数经过蜂群算法优化训练完成后，代入RBF神经网络模型继续进行训练. 训练完成后，利用训练好的IABC-RBF神经网络模型，对泾惠渠灌区研究区2006~2010年的地下水埋深进行预测.

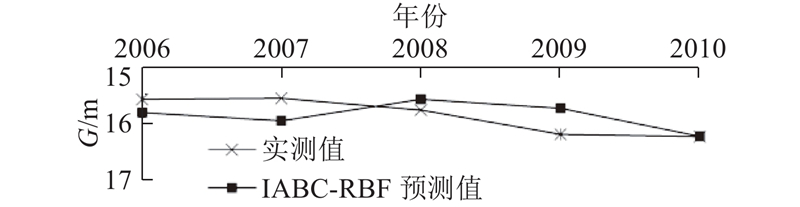
4.3. 预测结果

通过IABC-RBF神经网络模型预测泾惠渠灌区研究区的地下水埋深，预测结果与实测值的比较如图5所示. 如图5所示为将程序独立运行10次后的平均结果.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5 IABC-RBF神经网络模型预测值与实测值对比图

Fig.5 Comparison of predictive value and measured value of IABC-RBF neural network model

从图5可以看出，IABC-RBF神经网络模型预测值与实测值之间的误差很小，除了2007年和2009年的预测值与实测值相差略大，2006年、2008年和2010年3年的预测值和实测值十分接近. 将IABC-RBF神经网络模型的程序独立运行10次后的预测结果与RBF神经网络模型、基于IABC-RBF神经网络模型程序运行10次后的结果进行比较，计算10次独立运行后各个年份地下水埋深的预测值与实测值的平均相对误差MRE，结果如表2所示.

表 2 3种模型预测结果的对比

Tab.2 Comparison of prediction results of three prediction models

年份	实测值/m	模型	预测值/m			MRE/%
年份	实测值/m	模型	最优	最差	平均	MRE/%
2006	15.59	RBF	−	−	14.97	3.95
2006	15.59	ABC-RBF	15.76	16.07	15.85	1.66
2006	15.59	IABC-RBF	15.74	15.92	15.83	1.51
2007	15.57	RBF	−	−	14.56	6.46
2007	15.57	ABC-RBF	15.73	16.27	16.02	2.91
2007	15.57	IABC-RBF	15.79	16.18	15.97	2.58
2008	15.78	RBF	−	−	15.15	4.01
2008	15.78	ABC-RBF	15.69	15.32	15.55	1.44
2008	15.78	IABC-RBF	15.71	15.42	15.59	1.20
2009	16.21	RBF	−	−	17.19	6.08
2009	16.21	ABC-RBF	16.06	14.97	15.66	3.38
2009	16.21	IABC-RBF	16.06	15.59	15.75	3.04
2010	16.25	RBF	−	−	14.78	9.05
2010	16.25	ABC-RBF	16.25	16.04	16.20	0.68
2010	16.25	IABC-RBF	16.25	16.11	16.25	0.03

新窗口打开| 下载CSV

从表2的比较可以看出，IABC-RBF神经网络模型不仅在预测结果的最优值和最差值的精度上普遍略高于ABC-RBF神经网络模型，而且在预测结果的平均值上搜索精度明显更高，说明改进后的人工蜂群算法在稳定性和搜索精度方面均有一定的提高.

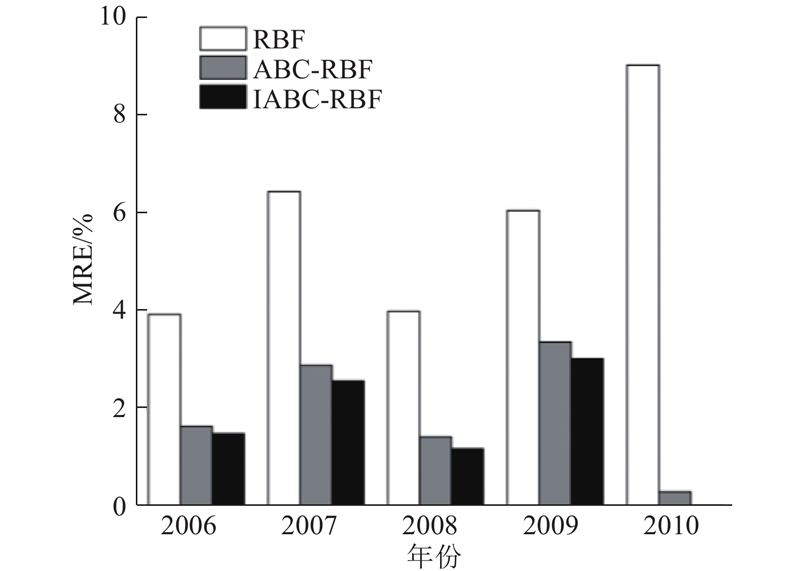
将各模型的程序运行10次后，各个年份的平均相对误差对比如图6所示. 可以看出，在模型预测结果的平均值上，IABC-RBF神经网络模型的精度最高.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6 3种模型预测结果的平均相对误差对比

Fig.6 Average relative error comparison of three models' prediction results

根据3种模型对5组预测样本的预测结果，计算3种模型预测结果的MRE及方差σ，对比如表3所示. 可以看出，IABC-RBF神经网络模型的稳定性和搜索精度最高.

表 3 预测结果的平均相对误差和方差对比

Tab.3 Comparison of average relative error and variance of three model prediction results

模型	MRE/%	σ/m
RBF模型	5.91	0.992 2
ABC-RBF模型	2.01	0.356 5
IABC-RBF模型	1.67	0.305 9

新窗口打开| 下载CSV

从图6和表2、3可以看出，在应用于泾惠渠灌区研究区的地下水埋深预测中，IABC-RBF神经网络模型和ABC-RBF神经网络模型的预测结果均显著优于未经算法优化训练的RBF神经网络模型. IABC-RBF神经网络模型的搜索精度略高于ABC-RBF神经网络模型，具有更好的稳定性.

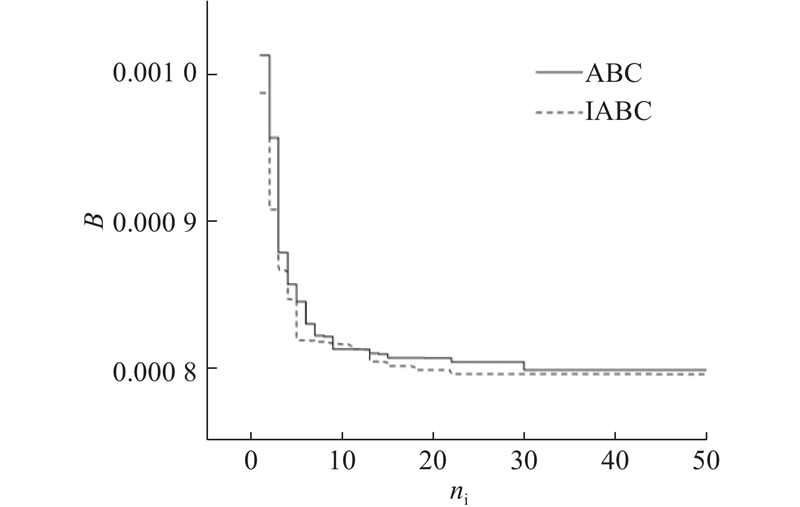
收敛速度是优化算法性能的一个重要指标. 将改进人工蜂群算法与基本人工蜂群算法每次迭代后的全局最佳值B进行比较，如图7所示. 图中，n_i为迭代次数.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7 每次迭代后的最佳值

Fig.7 Best cost of each iteration

从图7可以看出，改进后的蜂群算法相比于基本蜂群算法在迭代初期显示出更好的性能，收敛速度更快，经过50次迭代后的收敛精度更高.

5. 结　语

神经网络初始参数的设置对结果影响很大. 优化算法通过优化训练确定神经网络的相关参数，发挥了神经网络的广泛映射能力和优化算法的全局搜索能力，加快了网络学习速度.

本文在地下水埋深预测问题中，引入高斯变异算子，优化了初始解空间. 建立基于改进人工蜂群算法优化的RBF神经网络模型，运用改进的人工蜂群算法优化训练RBF神经网络模型的参数. 对泾惠渠灌区研究区的地下水埋深进行研究预测，结果表明，IABC-RBF神经网络模型的地下水埋深预测结果误差很小，将IABC-RBF神经网络模型与ABC-RBF神经网络模型和RBF神经网络模型进行对比，得出IABC-RBF神经网络模型和ABC-RBF神经网络模型的精度相对更高，IABC-RBF神经网络模型的搜索精度、稳定性和收敛速度均比ABC-RBF神经网络模型得到了提高.

地下水埋深的动态变化是一个复杂的过程，本文考虑到地表水的渗漏，将灌区的渠首引水量和田间灌水量作为影响因子，考虑到潜水的极限蒸发深度，没有将蒸发量作为影响因子. 从总体上来说，地下水埋深的影响因子还有土壤、地质等，建立的预测模型无法将所有的动态条件包含在内，只是在现有数据的基础上验证了IABC-RBF模型在地下水埋深预测中的可行性和优越性.

改进人工蜂群算法应用于地下水埋深预测的优越性需要更全面的数据和更完整的实验来进行验证. 针对人工蜂群算法的进一步改进，有待更深入的研究.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘东, 付强

三江平原井灌水稻地区地下水动态变化规律的小波神经网络分析

[J]. 灌溉排水学报, 2008, 27 (3): 86- 89