(34) ${{A}} = \left[ {\begin{array}{*{20}{c}} 1&{ - {\mu _{{\rm{cp}},2}}}&{ - {\mu _{{\rm{cp}},3}}}&0&0&0 \\ { - {\mu _{{\rm{cp}},1}}}&1&{ - {\mu _{{\rm{cp}},3}}}&0&0&0 \\ { - {\mu _{{\rm{cp}},1}}}&{ - {\mu _{{\rm{cp}},2}}}&1&0&0&0 \\ 0&0&0&{2 + {\mu _{{\rm{cp}},2}} + \;{\mu _{{\rm{cp}},3}}}&0&0 \\ 0&0&0&0&{2 + {\mu _{{\rm{cp}},1}} + {\mu _{{\rm{cp}},3}}}&0 \\ 0&0&0&0&0&{2 + {\mu _{{\rm{cp}},1}} + \;{\mu _{{\rm{cp}},2}}} \end{array}} \right].$
(43) $\left. \begin{aligned} &\begin{aligned} {{{\varepsilon }}_{\rm{c}}}({t_n}) = {{A}}\left[ {\Delta {{{\sigma }}_0}C\left( {{t_n},{t_0},{{{\sigma }}_{{t_0}}}} \right)} \right. + \cdots +\\ \;\left. {C\left( {{t_n},{t_{n - 1}},{{{\sigma }}_{{t_{n - 1}}}}} \right)\Delta {{{\sigma }}_{n - 1}}} \right],\;\;\;\;\end{aligned}\\ &\begin{aligned} {{{\varepsilon }}_{\rm{c}}}({t_{n + 1}}) =& {{A}}\left[ {\Delta {{{\sigma }}_0}C\left( {{t_{n + 1}},{t_0},{{{\sigma }}_{{t_0}}}} \right)} \right. + \cdots +\\ & \left. {C\left( {{t_{n + 1}},{t_n},{{{\sigma }}_{{t_n}}}} \right)\Delta {{{\sigma }}_n}} \right].\;\;\;\;\;\;\end{aligned} \end{aligned} \right\}$
(44) $\begin{split} &\Delta {{{\varepsilon }}_{\rm{c}}}({t_{n + 1}}) = \left[ {C\left( {{t_{n + 1}},{t_0},{{{\sigma }}_{{t_0}}}} \right) - C\left( {{t_n},{t_0},{{{\sigma }}_{{t_0}}}} \right)} \right]{{A}}\Delta {{{\sigma }}_0} + \cdots +\\ & \quad \left[ {C\left( {{t_{n + 1}},{t_{n - 1}},{{{\sigma }}_{{t_{n - 1}}}}} \right) - C\left( {{t_n},{t_{n - 1}},{{{\sigma }}_{{t_{n - 1}}}}} \right)} \right]\;{{A}}\Delta {{{\sigma }}_{n - 1}} + \\ &\quad\left[ {C\left( {{t_{n + 1}},{t_n},{{{\sigma }}_{{t_n}}}} \right)} \right]{{A}}\Delta {{{\sigma }}_n}. \end{split}$
[1]
陈宝春, 韦建刚, 周俊, 等 我国钢管混凝土拱桥应用现状与展望
[J]. 土木工程学报 , 2017 , 50 (6 ): 50 - 61
[本文引用: 1]
CHEN Bao-chun, WEI Jian-gang, ZHOU Jun, et al Application of concrete-filled steel tube arch bridges in China: current status and prospects
[J]. China Civil Engineering Journal , 2017 , 50 (6 ): 50 - 61
[本文引用: 1]
[2]
容柏生, 李盛勇, 陈洪涛, 等 中国高层建筑中钢管混凝土柱的应用与展望
[J]. 建筑结构 , 2009 , 39 (9 ): 33 - 38
RONG Bai-sheng, LI Sheng-yong, CHEN Hong-tao, et al Application and future perspective of concrete fill steel tube column in tall buildings
[J]. Building Structure , 2009 , 39 (9 ): 33 - 38
[3]
李为腾, 王乾, 杨宁, 等 钢管混凝土拱架在巷道支护中的发展与现状
[J]. 土木工程学报 , 2016 , 49 (11 ): 97 - 114
[本文引用: 1]
LI Wei-teng, WANG Qian, YANG Ning, et al Development and present status of concrete-filled steel tubular supporting arch in mine roadway
[J]. China Civil Engineering Journal , 2016 , 49 (11 ): 97 - 114
[本文引用: 1]
[4]
韩林海. 钢管混凝土结构—理论与实践[M]. 3版. 北京: 科学出版社, 2016: 1–26.
[本文引用: 1]
[5]
査晓雄. 空心和实心钢管混凝土[M]. 北京: 科学出版社, 2011: 1–7.
[6]
王元丰. 钢管混凝土徐变理论[M]. 北京: 科学出版社, 2013: 1–10.
[本文引用: 1]
[8]
WANG Y Y, GENG Y, RANZI G, et al Time-dependent behaviour of expansive concrete-filled steel tubular columns
[J]. Journal of Constructional Steel Research , 2011 , 67 (3 ): 471 - 483
DOI:10.1016/j.jcsr.2010.09.007
[9]
付学宝. 高应力状态下钢管混凝土短柱轴压长期性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.
[本文引用: 4]
FU Xue-bao. Long-term behavior of axially loaded concrete filled steel tubular stub columns under high stress [D]. Harbin: Harbin Institute of Technology, 2013.
[本文引用: 4]
[10]
MA Y S, WANG Y F, Mao Z K Creep effects on dynamic behavior of concrete filled steel tube arch bridge
[J]. Structural Engineering and Mechanics , 2011 , 37 (3 ): 321 - 330
DOI:10.12989/sem.2011.37.3.321
[本文引用: 1]
[11]
MA Y S, WANG Y F Creep influence on structural dynamic reliability
[J]. Engineering Structures , 2015 , (99 ): 1 - 8
[本文引用: 1]
[12]
HAN B, XIE H, ZHU L, et al Nonlinear model for early age creep of concrete under compression strains
[J]. Con-struction and Building Materials , 2017 , (147 ): 203 - 211
[本文引用: 1]
[13]
冯明珲, 吕和祥, 林皋, 等 粘弹塑性理论在混凝土变形中的应用
[J]. 工程力学 , 2002 , 19 (2 ): 3 - 8
[本文引用: 1]
FENG Ming-hui, LV He-xiang, LIN Gao, et al A unified visco-elastic-plastic constitutive model for concrete deformation
[J]. Engineering Mechanics , 2002 , 19 (2 ): 3 - 8
[本文引用: 1]
[14]
BAZANT Z P, KIM S S Nonlinear creep of con-crete-adaptation and flow
[J]. Journal of the Engineering Mechanics Division , 1979 , 105 : 429 - 446
[本文引用: 1]
[15]
林南薰 混凝土非线性徐变理论问题
[J]. 土木工程学报 , 1983 , 16 (1 ): 14 - 21
LIN Nan-xun Problems in the theory of nonlinear creep of concrete
[J]. China Civil Engineering Journal , 1983 , 16 (1 ): 14 - 21
[16]
刘杏红, 周创兵, 常晓林, 等 考虑非线性徐变的混凝土温度裂缝扩展过程模拟
[J]. 岩土力学 , 2010 , 31 (6 ): 1995 - 2000
DOI:10.3969/j.issn.1000-7598.2010.06.053
LIU Xing-hong, ZHOU Chuang-bing, CHANG Xiao-lin, et al Simulation of temperature crack propagation considering nonlinear creep of concrete
[J]. Rock and Soil Me-chanics , 2010 , 31 (6 ): 1995 - 2000
DOI:10.3969/j.issn.1000-7598.2010.06.053
[17]
HAMED E Modelling of creep in continuous RC beams under high levels of sustained loading
[J]. Mechanics of Time-dependent Materials , 2014 , 18 (3 ): 589 - 609
DOI:10.1007/s11043-014-9243-7
[本文引用: 1]
[19]
黄海东, 向中富 混凝土结构非线性徐变计算方法研究
[J]. 工程力学 , 2014 , 31 (2 ): 96 - 102
[本文引用: 2]
HUANG Hai-dong, XIANG Zhong-fu Nonlinear creep analysis method for concrete structures
[J]. Engineering Mechanics , 2014 , 31 (2 ): 96 - 102
[本文引用: 2]
[20]
张电杰, 王元丰, 雷扬 钢管混凝土轴心受压短柱徐变模型研究
[J]. 土木工程学报 , 2010 , 43 (Suppl. 2 ): 246 - 251
[本文引用: 2]
ZHANG Dan-jie, WANG Yang-feng, Lei Yang A new creep model for concrete filled steel tube columns under axial compression
[J]. China Civil Engineering Journal , 2010 , 43 (Suppl. 2 ): 246 - 251
[本文引用: 2]
[21]
MARÍ N R, BAIRÁN J M, DUARTE N Long-term deflections in cracked reinforced concrete flexural members
[J]. Engineering Structures , 2010 , 32 (3 ): 829 - 842
DOI:10.1016/j.engstruct.2009.12.009
[本文引用: 2]
[23]
牛艳伟, 石雪飞, 阮欣 混凝土结构三维徐变的有限元计算方法
[J]. 同济大学学报 , 2009 , 37 (4 ): 475 - 480
[本文引用: 1]
NIU Yan-wei, SHI Xue-fei, RUAN Xin A Finite element analysis method of concrete structure with three-dimensional creep
[J]. Journal of Tongji University , 2009 , 37 (4 ): 475 - 480
[本文引用: 1]
[24]
BAZANT Z P, WENDNER R RILEM draft recommendation: TC-242-MDC multi-decade creep and shrinkage of concrete: material model and structural analysis
[J]. Ma-terials and Structures , 2015 , 48 (4 ): 753 - 770
DOI:10.1617/s11527-014-0485-2
[本文引用: 2]
[25]
LUBLINER J, OLIVER J, OLLER S, et al A plas-tic-damage model for concrete
[J]. International Journal of Solids and Structures , 1989 , 25 (3 ): 299 - 326
DOI:10.1016/0020-7683(89)90050-4
[本文引用: 2]
[28]
ZHANG J, LI J Investigation into Lubliner yield criterion of concrete for 3D simulation
[J]. Engineering Structures , 2012 , (44 ): 122 - 127
[本文引用: 2]
[29]
CHEN W F. Plasticity in reinforced concrete [M]. New York: Mcgraw-hill, 1983.
[本文引用: 1]
[30]
江佳斐, 吴宇飞, 李奔奔. 约束混凝土内摩擦角的特性研究[C] // 第二十三届全国结构工程学术会议论文集(第Ⅱ册), 兰州: 全国结构工程学术会议, 2014: 47–51. JIANG J F, WU Y F, LI B B. Characteristic of internal friction angle for confined concrete [C] // Proceedings of the 23th National Academic Conference on Structural Engineering (Vol. II) . Lanzhou: ISSE, 2014: 47-51
[本文引用: 1]
[31]
JIANG J F, WU Y F Identification of material parameters for Drucker-Prager plasticity model for FRP confined cir-cular concrete columns
[J]. International Journal of Solids and Structures , 2011 , 49 (3 ): 445 - 456
[本文引用: 1]
[32]
TAO Z, WANG Z B, YU Q Finite element modelling of concrete-filled steel stub columns under axial compression
[J]. Journal of Constructional Steel Research , 2013 , (89 ): 121 - 131
[本文引用: 2]
[33]
WANG Y B, LIEW J Y R Constitutive model for confined ultra-high strength concrete in steel tube
[J]. Construction and Building Materials , 2016 , (126 ): 812 - 822
[本文引用: 2]
[34]
秦浩, 赵宪忠 ABAQUS混凝土损伤因子取值方法研究
[J]. 结构工程师 , 2013 , (29 ): 27 - 32
[本文引用: 3]
QIN Hao, ZHAO Xian-zhong Study on the ABAQUS damage parameter in the concrete damage plasticity model
[J]. Structural Engineers , 2013 , (29 ): 27 - 32
[本文引用: 3]
[35]
MAZZOTTI C, SAVOIA M Nonlinear creep, Poisson's ratio, and creep-damage interaction of concrete in compression
[J]. ACI Materials Journal , 2002 , 99 (5 ): 450 - 457
[本文引用: 1]
[36]
黄国兴, 惠荣炎, 王秀军. 混凝土徐变与收缩[M]. 北京: 中国电力出版社, 2012: 52-55.
[37]
NEVILLE A M, DILGER W H, BROOKS J J. Creep of plain and structural concrete [M]. New York: Construc-tion Press, 1983.
[本文引用: 1]
[38]
林军. 核心混凝土的徐变及其对钢管高强混凝土轴压构件力学性能的影响[D]. 汕头: 汕头大学, 2002.
[本文引用: 3]
LIN Jun. The creep of core concrete and its influence on the mechanical performance of the axially compressed high strength concrete filled steel tubular member [D]. Shantou: Shantou University, 2002.
[本文引用: 3]
[39]
AL-MANASEER A, PRADO A Statistical comparisons of creep and shrinkage prediction models using RILEM and NU-ITI databases
[J]. ACI Materials Journal , 2015 , 112 (6 ): 829 - 831
[本文引用: 1]
[40]
ZHANG J, WANG J H, GAO Y Moisture movement in early ages concrete under cement hydration and environmental drying
[J]. Magazine of Concrete Research , 2016 , 68 (8 ): 391 - 408
DOI:10.1680/jmacr.15.00293
[本文引用: 1]
[41]
XIANG X Y, CAI C S, ZHAO R D, et al Numerical analysis of recycled aggregate concrete-filled steel tube stub columns
[J]. Advances in Structural Engineering , 2016 , 19 (5 ): 717 - 729
DOI:10.1177/1369433215618270
[本文引用: 1]
我国钢管混凝土拱桥应用现状与展望
1
2017
... 钢管混凝土(concrete-filled steel tube, CFST)结构因承载能力较高,塑性、抗震性能较好等优点,在大跨桥梁、高层及超高层建筑、地铁站等结构的受压构件中得到广泛运用,同时因其充分发挥了钢与混凝土材料的力学性能,表现出良好的经济效果[1 -3 ] . ...
我国钢管混凝土拱桥应用现状与展望
1
2017
... 钢管混凝土(concrete-filled steel tube, CFST)结构因承载能力较高,塑性、抗震性能较好等优点,在大跨桥梁、高层及超高层建筑、地铁站等结构的受压构件中得到广泛运用,同时因其充分发挥了钢与混凝土材料的力学性能,表现出良好的经济效果[1 -3 ] . ...
钢管混凝土拱架在巷道支护中的发展与现状
1
2016
... 钢管混凝土(concrete-filled steel tube, CFST)结构因承载能力较高,塑性、抗震性能较好等优点,在大跨桥梁、高层及超高层建筑、地铁站等结构的受压构件中得到广泛运用,同时因其充分发挥了钢与混凝土材料的力学性能,表现出良好的经济效果[1 -3 ] . ...
钢管混凝土拱架在巷道支护中的发展与现状
1
2016
... 钢管混凝土(concrete-filled steel tube, CFST)结构因承载能力较高,塑性、抗震性能较好等优点,在大跨桥梁、高层及超高层建筑、地铁站等结构的受压构件中得到广泛运用,同时因其充分发挥了钢与混凝土材料的力学性能,表现出良好的经济效果[1 -3 ] . ...
1
... 大量研究结果均表明,混凝土徐变会引起结构变形和内力重分布,对CFST的长期结构行为有重要影响[4 -6 ] . 试验研究和理论分析均表明,当核心混凝土应力超过一定水平时(0.6f cm ,f cm 为圆柱体抗压强度平均值),徐变与应力之间表现出明显的非线性特征[7 -9 ] . 付学宝等[9 ] 分析计算了厦门港务大厦、昆明大成金融商务中心等超高层建筑的CFST柱核心混凝土应力水平,发现部分已达0.69f cm . 高应力下的非线性徐变效应不仅会使CFST结构出现过大的变形,还会进一步影响结构的动力特性与响应[10 -11 ] . 为准确分析高应力水平下的CFST长期结构行为,需要建立非线性徐变分析理论. ...
1
... 大量研究结果均表明,混凝土徐变会引起结构变形和内力重分布,对CFST的长期结构行为有重要影响[4 -6 ] . 试验研究和理论分析均表明,当核心混凝土应力超过一定水平时(0.6f cm ,f cm 为圆柱体抗压强度平均值),徐变与应力之间表现出明显的非线性特征[7 -9 ] . 付学宝等[9 ] 分析计算了厦门港务大厦、昆明大成金融商务中心等超高层建筑的CFST柱核心混凝土应力水平,发现部分已达0.69f cm . 高应力下的非线性徐变效应不仅会使CFST结构出现过大的变形,还会进一步影响结构的动力特性与响应[10 -11 ] . 为准确分析高应力水平下的CFST长期结构行为,需要建立非线性徐变分析理论. ...
长期荷载作用对圆钢管混凝土压弯构件力学性能影响的研究
1
2002
... 大量研究结果均表明,混凝土徐变会引起结构变形和内力重分布,对CFST的长期结构行为有重要影响[4 -6 ] . 试验研究和理论分析均表明,当核心混凝土应力超过一定水平时(0.6f cm ,f cm 为圆柱体抗压强度平均值),徐变与应力之间表现出明显的非线性特征[7 -9 ] . 付学宝等[9 ] 分析计算了厦门港务大厦、昆明大成金融商务中心等超高层建筑的CFST柱核心混凝土应力水平,发现部分已达0.69f cm . 高应力下的非线性徐变效应不仅会使CFST结构出现过大的变形,还会进一步影响结构的动力特性与响应[10 -11 ] . 为准确分析高应力水平下的CFST长期结构行为,需要建立非线性徐变分析理论. ...
长期荷载作用对圆钢管混凝土压弯构件力学性能影响的研究
1
2002
... 大量研究结果均表明,混凝土徐变会引起结构变形和内力重分布,对CFST的长期结构行为有重要影响[4 -6 ] . 试验研究和理论分析均表明,当核心混凝土应力超过一定水平时(0.6f cm ,f cm 为圆柱体抗压强度平均值),徐变与应力之间表现出明显的非线性特征[7 -9 ] . 付学宝等[9 ] 分析计算了厦门港务大厦、昆明大成金融商务中心等超高层建筑的CFST柱核心混凝土应力水平,发现部分已达0.69f cm . 高应力下的非线性徐变效应不仅会使CFST结构出现过大的变形,还会进一步影响结构的动力特性与响应[10 -11 ] . 为准确分析高应力水平下的CFST长期结构行为,需要建立非线性徐变分析理论. ...
Time-dependent behaviour of expansive concrete-filled steel tubular columns
2011
4
... 大量研究结果均表明,混凝土徐变会引起结构变形和内力重分布,对CFST的长期结构行为有重要影响[4 -6 ] . 试验研究和理论分析均表明,当核心混凝土应力超过一定水平时(0.6f cm ,f cm 为圆柱体抗压强度平均值),徐变与应力之间表现出明显的非线性特征[7 -9 ] . 付学宝等[9 ] 分析计算了厦门港务大厦、昆明大成金融商务中心等超高层建筑的CFST柱核心混凝土应力水平,发现部分已达0.69f cm . 高应力下的非线性徐变效应不仅会使CFST结构出现过大的变形,还会进一步影响结构的动力特性与响应[10 -11 ] . 为准确分析高应力水平下的CFST长期结构行为,需要建立非线性徐变分析理论. ...
... [9 ]分析计算了厦门港务大厦、昆明大成金融商务中心等超高层建筑的CFST柱核心混凝土应力水平,发现部分已达0.69f cm . 高应力下的非线性徐变效应不仅会使CFST结构出现过大的变形,还会进一步影响结构的动力特性与响应[10 -11 ] . 为准确分析高应力水平下的CFST长期结构行为,需要建立非线性徐变分析理论. ...
... 付学宝等[9 , 38 ] 分别进行了不同应力水平作用下的轴压圆CFST短柱徐变试验,为便于描述,简记为试验I与试验II. 各试件尺寸、加载荷载、应力水平等如表1 所示,D 为圆柱体试件外径;T 为钢管厚度;h 为时间高度;F 为试验荷载大小;n c 表示混凝土应力水平,为核心混凝土的初始应力和圆柱体抗压强度平均值之比. ...
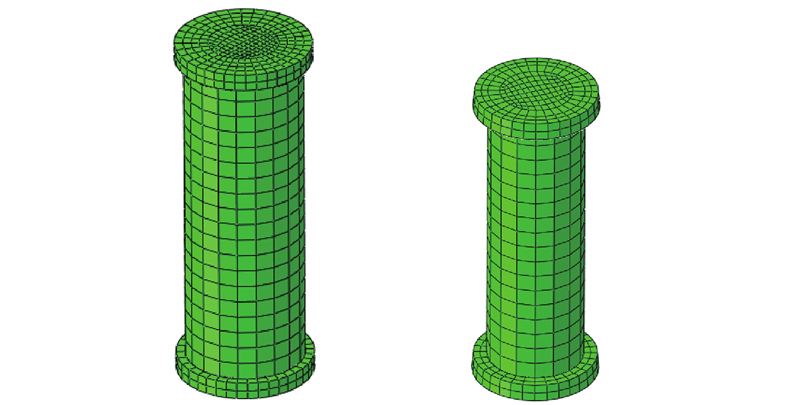
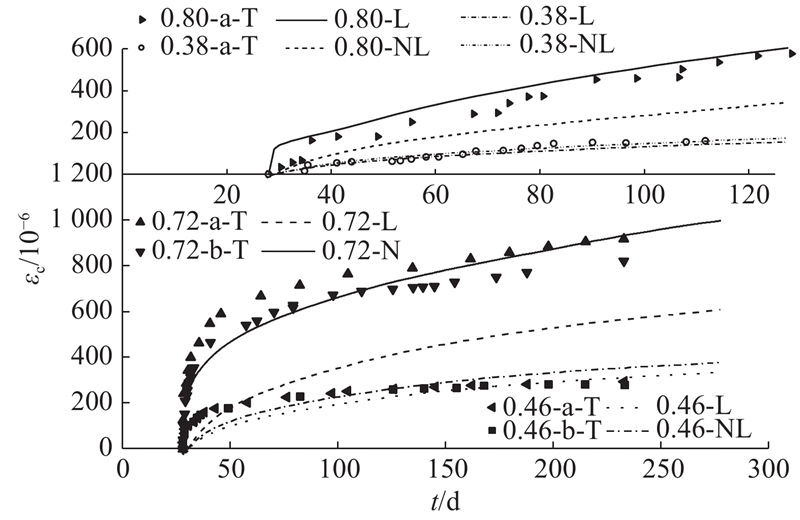
... 选用ABAQUS软件对试件进行有限元模拟,混凝土和钢管分别采用实体单元C3D8、C3D8I,钢管与混凝土交界面法向采用“硬接触”模拟,切向采用摩擦罚函数模拟,界面摩擦系数取0.25[41 ] . 假定垫板为不变形刚体,垫板与钢和混凝土的连结采用绑定约束. 由于无该试件受压全过程荷载位移曲线实测数据,膨胀角按式(24)进行计算,试验I与试验II试件的膨胀角分别为27.5°与34.1°,其他参数计算参见文献[34 ]. 有限元网格模型如图4 所示. 文献[9 ]与[38 ]的实测应变与分析结果对比如图5 所示,图中T表示试验组. ...
4
... 大量研究结果均表明,混凝土徐变会引起结构变形和内力重分布,对CFST的长期结构行为有重要影响[4 -6 ] . 试验研究和理论分析均表明,当核心混凝土应力超过一定水平时(0.6f cm ,f cm 为圆柱体抗压强度平均值),徐变与应力之间表现出明显的非线性特征[7 -9 ] . 付学宝等[9 ] 分析计算了厦门港务大厦、昆明大成金融商务中心等超高层建筑的CFST柱核心混凝土应力水平,发现部分已达0.69f cm . 高应力下的非线性徐变效应不仅会使CFST结构出现过大的变形,还会进一步影响结构的动力特性与响应[10 -11 ] . 为准确分析高应力水平下的CFST长期结构行为,需要建立非线性徐变分析理论. ...
... [9 ]分析计算了厦门港务大厦、昆明大成金融商务中心等超高层建筑的CFST柱核心混凝土应力水平,发现部分已达0.69f cm . 高应力下的非线性徐变效应不仅会使CFST结构出现过大的变形,还会进一步影响结构的动力特性与响应[10 -11 ] . 为准确分析高应力水平下的CFST长期结构行为,需要建立非线性徐变分析理论. ...
... 付学宝等[9 , 38 ] 分别进行了不同应力水平作用下的轴压圆CFST短柱徐变试验,为便于描述,简记为试验I与试验II. 各试件尺寸、加载荷载、应力水平等如表1 所示,D 为圆柱体试件外径;T 为钢管厚度;h 为时间高度;F 为试验荷载大小;n c 表示混凝土应力水平,为核心混凝土的初始应力和圆柱体抗压强度平均值之比. ...
... 选用ABAQUS软件对试件进行有限元模拟,混凝土和钢管分别采用实体单元C3D8、C3D8I,钢管与混凝土交界面法向采用“硬接触”模拟,切向采用摩擦罚函数模拟,界面摩擦系数取0.25[41 ] . 假定垫板为不变形刚体,垫板与钢和混凝土的连结采用绑定约束. 由于无该试件受压全过程荷载位移曲线实测数据,膨胀角按式(24)进行计算,试验I与试验II试件的膨胀角分别为27.5°与34.1°,其他参数计算参见文献[34 ]. 有限元网格模型如图4 所示. 文献[9 ]与[38 ]的实测应变与分析结果对比如图5 所示,图中T表示试验组. ...
Creep effects on dynamic behavior of concrete filled steel tube arch bridge
1
2011
... 大量研究结果均表明,混凝土徐变会引起结构变形和内力重分布,对CFST的长期结构行为有重要影响[4 -6 ] . 试验研究和理论分析均表明,当核心混凝土应力超过一定水平时(0.6f cm ,f cm 为圆柱体抗压强度平均值),徐变与应力之间表现出明显的非线性特征[7 -9 ] . 付学宝等[9 ] 分析计算了厦门港务大厦、昆明大成金融商务中心等超高层建筑的CFST柱核心混凝土应力水平,发现部分已达0.69f cm . 高应力下的非线性徐变效应不仅会使CFST结构出现过大的变形,还会进一步影响结构的动力特性与响应[10 -11 ] . 为准确分析高应力水平下的CFST长期结构行为,需要建立非线性徐变分析理论. ...
Creep influence on structural dynamic reliability
1
2015
... 大量研究结果均表明,混凝土徐变会引起结构变形和内力重分布,对CFST的长期结构行为有重要影响[4 -6 ] . 试验研究和理论分析均表明,当核心混凝土应力超过一定水平时(0.6f cm ,f cm 为圆柱体抗压强度平均值),徐变与应力之间表现出明显的非线性特征[7 -9 ] . 付学宝等[9 ] 分析计算了厦门港务大厦、昆明大成金融商务中心等超高层建筑的CFST柱核心混凝土应力水平,发现部分已达0.69f cm . 高应力下的非线性徐变效应不仅会使CFST结构出现过大的变形,还会进一步影响结构的动力特性与响应[10 -11 ] . 为准确分析高应力水平下的CFST长期结构行为,需要建立非线性徐变分析理论. ...
Nonlinear model for early age creep of concrete under compression strains
1
2017
... 对于非线性徐变理论,现有的研究方法主要有3类:一类是直接通过高应力下的单轴受力徐变试验,建立模拟徐变特性的流变模型[12 -13 ] ;另一类是以低应力下的单轴徐变特性为基础,建立徐变应变和应力之间的非线性函数关系[14 -17 ] ;还有一类是采用损伤力学的方法来建立高应力下混凝土的非线性徐变本构方程[18 -19 ] . 前2类方法均是从单轴常应力作用下的徐变试验出发,很难将其运用到复杂空间应力状态下的徐变效应分析;第三类方法把非线性徐变产生的原因归结为高应力下的材料损伤演化,在实际工程中得到广泛运用,但已有研究成果也存在一定不足. 如李兆霞等[18 ] 运用连续介质损伤力学建立了弹性徐变损伤分析模型,并未涉及高应力下材料塑性行为的影响. 黄海东等[19 ] 运用经典的单轴应力应变关系(Hongnestad模型)探讨了混凝土非线性徐变效应的分析方法,而单轴应力应变曲线并不能完整描述混凝土材料的非线性行为. ...
粘弹塑性理论在混凝土变形中的应用
1
2002
... 对于非线性徐变理论,现有的研究方法主要有3类:一类是直接通过高应力下的单轴受力徐变试验,建立模拟徐变特性的流变模型[12 -13 ] ;另一类是以低应力下的单轴徐变特性为基础,建立徐变应变和应力之间的非线性函数关系[14 -17 ] ;还有一类是采用损伤力学的方法来建立高应力下混凝土的非线性徐变本构方程[18 -19 ] . 前2类方法均是从单轴常应力作用下的徐变试验出发,很难将其运用到复杂空间应力状态下的徐变效应分析;第三类方法把非线性徐变产生的原因归结为高应力下的材料损伤演化,在实际工程中得到广泛运用,但已有研究成果也存在一定不足. 如李兆霞等[18 ] 运用连续介质损伤力学建立了弹性徐变损伤分析模型,并未涉及高应力下材料塑性行为的影响. 黄海东等[19 ] 运用经典的单轴应力应变关系(Hongnestad模型)探讨了混凝土非线性徐变效应的分析方法,而单轴应力应变曲线并不能完整描述混凝土材料的非线性行为. ...
粘弹塑性理论在混凝土变形中的应用
1
2002
... 对于非线性徐变理论,现有的研究方法主要有3类:一类是直接通过高应力下的单轴受力徐变试验,建立模拟徐变特性的流变模型[12 -13 ] ;另一类是以低应力下的单轴徐变特性为基础,建立徐变应变和应力之间的非线性函数关系[14 -17 ] ;还有一类是采用损伤力学的方法来建立高应力下混凝土的非线性徐变本构方程[18 -19 ] . 前2类方法均是从单轴常应力作用下的徐变试验出发,很难将其运用到复杂空间应力状态下的徐变效应分析;第三类方法把非线性徐变产生的原因归结为高应力下的材料损伤演化,在实际工程中得到广泛运用,但已有研究成果也存在一定不足. 如李兆霞等[18 ] 运用连续介质损伤力学建立了弹性徐变损伤分析模型,并未涉及高应力下材料塑性行为的影响. 黄海东等[19 ] 运用经典的单轴应力应变关系(Hongnestad模型)探讨了混凝土非线性徐变效应的分析方法,而单轴应力应变曲线并不能完整描述混凝土材料的非线性行为. ...
Nonlinear creep of con-crete-adaptation and flow
1
1979
... 对于非线性徐变理论,现有的研究方法主要有3类:一类是直接通过高应力下的单轴受力徐变试验,建立模拟徐变特性的流变模型[12 -13 ] ;另一类是以低应力下的单轴徐变特性为基础,建立徐变应变和应力之间的非线性函数关系[14 -17 ] ;还有一类是采用损伤力学的方法来建立高应力下混凝土的非线性徐变本构方程[18 -19 ] . 前2类方法均是从单轴常应力作用下的徐变试验出发,很难将其运用到复杂空间应力状态下的徐变效应分析;第三类方法把非线性徐变产生的原因归结为高应力下的材料损伤演化,在实际工程中得到广泛运用,但已有研究成果也存在一定不足. 如李兆霞等[18 ] 运用连续介质损伤力学建立了弹性徐变损伤分析模型,并未涉及高应力下材料塑性行为的影响. 黄海东等[19 ] 运用经典的单轴应力应变关系(Hongnestad模型)探讨了混凝土非线性徐变效应的分析方法,而单轴应力应变曲线并不能完整描述混凝土材料的非线性行为. ...
考虑非线性徐变的混凝土温度裂缝扩展过程模拟
2010
考虑非线性徐变的混凝土温度裂缝扩展过程模拟
2010
Modelling of creep in continuous RC beams under high levels of sustained loading
1
2014
... 对于非线性徐变理论,现有的研究方法主要有3类:一类是直接通过高应力下的单轴受力徐变试验,建立模拟徐变特性的流变模型[12 -13 ] ;另一类是以低应力下的单轴徐变特性为基础,建立徐变应变和应力之间的非线性函数关系[14 -17 ] ;还有一类是采用损伤力学的方法来建立高应力下混凝土的非线性徐变本构方程[18 -19 ] . 前2类方法均是从单轴常应力作用下的徐变试验出发,很难将其运用到复杂空间应力状态下的徐变效应分析;第三类方法把非线性徐变产生的原因归结为高应力下的材料损伤演化,在实际工程中得到广泛运用,但已有研究成果也存在一定不足. 如李兆霞等[18 ] 运用连续介质损伤力学建立了弹性徐变损伤分析模型,并未涉及高应力下材料塑性行为的影响. 黄海东等[19 ] 运用经典的单轴应力应变关系(Hongnestad模型)探讨了混凝土非线性徐变效应的分析方法,而单轴应力应变曲线并不能完整描述混凝土材料的非线性行为. ...
混凝土徐变损伤演变方程及其在非线性徐变理论中的应用
2
1989
... 对于非线性徐变理论,现有的研究方法主要有3类:一类是直接通过高应力下的单轴受力徐变试验,建立模拟徐变特性的流变模型[12 -13 ] ;另一类是以低应力下的单轴徐变特性为基础,建立徐变应变和应力之间的非线性函数关系[14 -17 ] ;还有一类是采用损伤力学的方法来建立高应力下混凝土的非线性徐变本构方程[18 -19 ] . 前2类方法均是从单轴常应力作用下的徐变试验出发,很难将其运用到复杂空间应力状态下的徐变效应分析;第三类方法把非线性徐变产生的原因归结为高应力下的材料损伤演化,在实际工程中得到广泛运用,但已有研究成果也存在一定不足. 如李兆霞等[18 ] 运用连续介质损伤力学建立了弹性徐变损伤分析模型,并未涉及高应力下材料塑性行为的影响. 黄海东等[19 ] 运用经典的单轴应力应变关系(Hongnestad模型)探讨了混凝土非线性徐变效应的分析方法,而单轴应力应变曲线并不能完整描述混凝土材料的非线性行为. ...
... [18 ]运用连续介质损伤力学建立了弹性徐变损伤分析模型,并未涉及高应力下材料塑性行为的影响. 黄海东等[19 ] 运用经典的单轴应力应变关系(Hongnestad模型)探讨了混凝土非线性徐变效应的分析方法,而单轴应力应变曲线并不能完整描述混凝土材料的非线性行为. ...
混凝土徐变损伤演变方程及其在非线性徐变理论中的应用
2
1989
... 对于非线性徐变理论,现有的研究方法主要有3类:一类是直接通过高应力下的单轴受力徐变试验,建立模拟徐变特性的流变模型[12 -13 ] ;另一类是以低应力下的单轴徐变特性为基础,建立徐变应变和应力之间的非线性函数关系[14 -17 ] ;还有一类是采用损伤力学的方法来建立高应力下混凝土的非线性徐变本构方程[18 -19 ] . 前2类方法均是从单轴常应力作用下的徐变试验出发,很难将其运用到复杂空间应力状态下的徐变效应分析;第三类方法把非线性徐变产生的原因归结为高应力下的材料损伤演化,在实际工程中得到广泛运用,但已有研究成果也存在一定不足. 如李兆霞等[18 ] 运用连续介质损伤力学建立了弹性徐变损伤分析模型,并未涉及高应力下材料塑性行为的影响. 黄海东等[19 ] 运用经典的单轴应力应变关系(Hongnestad模型)探讨了混凝土非线性徐变效应的分析方法,而单轴应力应变曲线并不能完整描述混凝土材料的非线性行为. ...
... [18 ]运用连续介质损伤力学建立了弹性徐变损伤分析模型,并未涉及高应力下材料塑性行为的影响. 黄海东等[19 ] 运用经典的单轴应力应变关系(Hongnestad模型)探讨了混凝土非线性徐变效应的分析方法,而单轴应力应变曲线并不能完整描述混凝土材料的非线性行为. ...
混凝土结构非线性徐变计算方法研究
2
2014
... 对于非线性徐变理论,现有的研究方法主要有3类:一类是直接通过高应力下的单轴受力徐变试验,建立模拟徐变特性的流变模型[12 -13 ] ;另一类是以低应力下的单轴徐变特性为基础,建立徐变应变和应力之间的非线性函数关系[14 -17 ] ;还有一类是采用损伤力学的方法来建立高应力下混凝土的非线性徐变本构方程[18 -19 ] . 前2类方法均是从单轴常应力作用下的徐变试验出发,很难将其运用到复杂空间应力状态下的徐变效应分析;第三类方法把非线性徐变产生的原因归结为高应力下的材料损伤演化,在实际工程中得到广泛运用,但已有研究成果也存在一定不足. 如李兆霞等[18 ] 运用连续介质损伤力学建立了弹性徐变损伤分析模型,并未涉及高应力下材料塑性行为的影响. 黄海东等[19 ] 运用经典的单轴应力应变关系(Hongnestad模型)探讨了混凝土非线性徐变效应的分析方法,而单轴应力应变曲线并不能完整描述混凝土材料的非线性行为. ...
... [19 ]运用经典的单轴应力应变关系(Hongnestad模型)探讨了混凝土非线性徐变效应的分析方法,而单轴应力应变曲线并不能完整描述混凝土材料的非线性行为. ...
混凝土结构非线性徐变计算方法研究
2
2014
... 对于非线性徐变理论,现有的研究方法主要有3类:一类是直接通过高应力下的单轴受力徐变试验,建立模拟徐变特性的流变模型[12 -13 ] ;另一类是以低应力下的单轴徐变特性为基础,建立徐变应变和应力之间的非线性函数关系[14 -17 ] ;还有一类是采用损伤力学的方法来建立高应力下混凝土的非线性徐变本构方程[18 -19 ] . 前2类方法均是从单轴常应力作用下的徐变试验出发,很难将其运用到复杂空间应力状态下的徐变效应分析;第三类方法把非线性徐变产生的原因归结为高应力下的材料损伤演化,在实际工程中得到广泛运用,但已有研究成果也存在一定不足. 如李兆霞等[18 ] 运用连续介质损伤力学建立了弹性徐变损伤分析模型,并未涉及高应力下材料塑性行为的影响. 黄海东等[19 ] 运用经典的单轴应力应变关系(Hongnestad模型)探讨了混凝土非线性徐变效应的分析方法,而单轴应力应变曲线并不能完整描述混凝土材料的非线性行为. ...
... [19 ]运用经典的单轴应力应变关系(Hongnestad模型)探讨了混凝土非线性徐变效应的分析方法,而单轴应力应变曲线并不能完整描述混凝土材料的非线性行为. ...
钢管混凝土轴心受压短柱徐变模型研究
2
2010
... 除此之外,轴压圆CFST短柱核心混凝土应力状态具有明显的三向受压特征,因此,其徐变特性还具有明显的三维特性[20 -23 ] . ...
... 目前关于多轴不同应力水平作用下的徐变规律研究还不成熟,没有直接可供借鉴的预测模型,本文拟通过引入徐变泊松比的概念,把单轴徐变规律拓展到多轴应力状态下,文献[20 ]、[34 ]采用了类似的方法. ...
钢管混凝土轴心受压短柱徐变模型研究
2
2010
... 除此之外,轴压圆CFST短柱核心混凝土应力状态具有明显的三向受压特征,因此,其徐变特性还具有明显的三维特性[20 -23 ] . ...
... 目前关于多轴不同应力水平作用下的徐变规律研究还不成熟,没有直接可供借鉴的预测模型,本文拟通过引入徐变泊松比的概念,把单轴徐变规律拓展到多轴应力状态下,文献[20 ]、[34 ]采用了类似的方法. ...
Long-term deflections in cracked reinforced concrete flexural members
2
2010
... 参数a i τ )与λ i [21 ] 确定: ...
... 混凝土的收缩徐变会使CFST柱产生内力重分配. 在众多的分析方法中,逐步递推分析方法能够较为方便的处理这一复杂过程,且能与现有通用有限元程序相结合[21 -22 ] ,其关键在于任意时间步Δt i
PC箱梁桥三维徐变效应精细化分析
1
2013
... 混凝土的收缩徐变会使CFST柱产生内力重分配. 在众多的分析方法中,逐步递推分析方法能够较为方便的处理这一复杂过程,且能与现有通用有限元程序相结合[21 -22 ] ,其关键在于任意时间步Δt i
PC箱梁桥三维徐变效应精细化分析
1
2013
... 混凝土的收缩徐变会使CFST柱产生内力重分配. 在众多的分析方法中,逐步递推分析方法能够较为方便的处理这一复杂过程,且能与现有通用有限元程序相结合[21 -22 ] ,其关键在于任意时间步Δt i
混凝土结构三维徐变的有限元计算方法
1
2009
... 除此之外,轴压圆CFST短柱核心混凝土应力状态具有明显的三向受压特征,因此,其徐变特性还具有明显的三维特性[20 -23 ] . ...
混凝土结构三维徐变的有限元计算方法
1
2009
... 除此之外,轴压圆CFST短柱核心混凝土应力状态具有明显的三向受压特征,因此,其徐变特性还具有明显的三维特性[20 -23 ] . ...
RILEM draft recommendation: TC-242-MDC multi-decade creep and shrinkage of concrete: material model and structural analysis
2
2015
... 为准确分析高应力下轴压圆CFST短柱徐变效应,本文基于混凝土弹塑性理论和连续损伤介质力学,提出一种新的高应力水平下的轴压圆CFST柱三维非线性徐变效应分析理论框架. 该框架首先包括均匀约束条件下的混凝土塑性损伤本构模型,用以模拟高应力作用下混凝土塑性和损伤演化;其次是CFST三维非线性徐变分析模型和相应的数值分析方法. 最后,本研究基于徐变预测B4模型[24 ] ,结合通用有限元软件ABAQUS,二次开发计算程序,通过不同应力水平下的CFST短柱徐变试验,验证所提方法的可靠性. ...
... 本文所涉及到的参数计算结果如表3 所示. 参数q 2 ~q 4 的取值与混凝土配合比、养护温度等相关,计算方法详见文献[24 ]. ...
A plas-tic-damage model for concrete
2
1989
... Lubliner等[25 -26 ] 提出的混凝土塑性损伤本构模型因为具有概念清晰、简便易用等优点,在实际工程中得到广泛应用,该本构模型主要包括Lubliner屈服准则、Drucker-Prager塑性流动准则、损伤演化与硬化准则等,主要适用于低围压应力下的混凝土结构弹塑性行为分析. 对轴压圆CFST柱而言,环向围压已经影响到混凝土的力学行为,对低围压下的塑性损伤本构模型进行合理修正,以适用于均匀约束条件下混凝土的弹塑性行为分析,不失为一种便捷有效的方法. ...
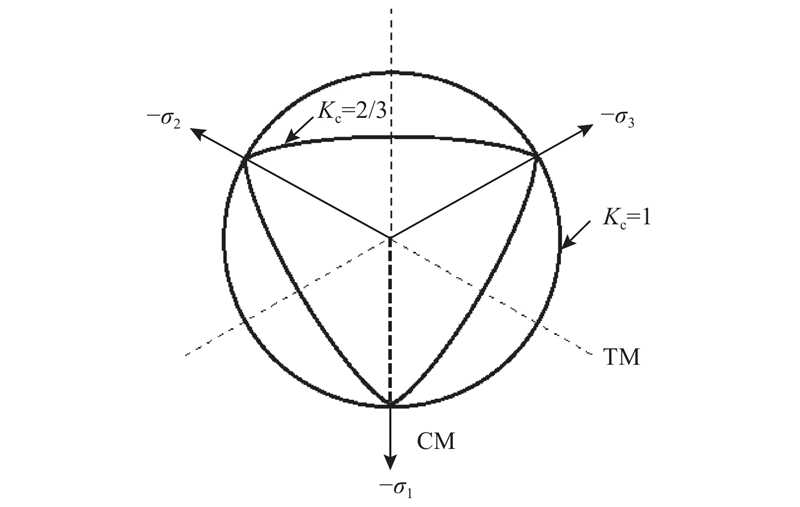
... 式中: $\tilde\varepsilon^{\rm p} $ x 〉=(|x |+x )/2;I 1 、J 2 分别为第一应力张量不变量和第二偏应力张量不变量; ${{{\bar{{\sigma }}}}_{\max }}$ ${{\bar \sigma }}$ c 为混凝土黏聚力;参数α 、β 由混凝土单轴拉压强度和双轴等压强度确定,具体过程可参见文献[26 ];在文献[25 ]、[26 ]中,参数γ 通过拉子午线(tensile meridian, TM)与压子午线(compression meridian, CM)来确定,这种方法对于轴压CFST柱而言,存在着无法避免的缺陷[27 ] ,详细阐述如下. ...
Plastic-damage model for cyclic loading of concrete structures
7
1998
... Lubliner等[25 -26 ] 提出的混凝土塑性损伤本构模型因为具有概念清晰、简便易用等优点,在实际工程中得到广泛应用,该本构模型主要包括Lubliner屈服准则、Drucker-Prager塑性流动准则、损伤演化与硬化准则等,主要适用于低围压应力下的混凝土结构弹塑性行为分析. 对轴压圆CFST柱而言,环向围压已经影响到混凝土的力学行为,对低围压下的塑性损伤本构模型进行合理修正,以适用于均匀约束条件下混凝土的弹塑性行为分析,不失为一种便捷有效的方法. ...
... 式中: $\tilde\varepsilon^{\rm p} $ x 〉=(|x |+x )/2;I 1 、J 2 分别为第一应力张量不变量和第二偏应力张量不变量; ${{{\bar{{\sigma }}}}_{\max }}$ ${{\bar \sigma }}$ c 为混凝土黏聚力;参数α 、β 由混凝土单轴拉压强度和双轴等压强度确定,具体过程可参见文献[26 ];在文献[25 ]、[26 ]中,参数γ 通过拉子午线(tensile meridian, TM)与压子午线(compression meridian, CM)来确定,这种方法对于轴压CFST柱而言,存在着无法避免的缺陷[27 ] ,详细阐述如下. ...
... ]、[26 ]中,参数γ 通过拉子午线(tensile meridian, TM)与压子午线(compression meridian, CM)来确定,这种方法对于轴压CFST柱而言,存在着无法避免的缺陷[27 ] ,详细阐述如下. ...
... 因ζ 通常取0.1[26 ] , ${\left[ {{{\left( {\zeta {\sigma _{{\rm{t}}0}}\tan \psi } \right)}^2} + 3{J_2}} \right]^{1/2}} \approx \sqrt {3{J_2}} $
... 根据文献[26 ],引入损伤因子d ,应力张量σ ε
... 由于0>σ 1 =σ 2 >σ 3 ,由式(30)可得, $r\left( {{\hat{ \sigma }}} \right)$ 26 ],通常 ${s_{\rm{t}}} = 1$ ${s_{\rm{c}}} = 0$
... 式中:d c 的计算方法可参见文献[34 ]. 根据文献[26 ],混凝土的屈服面演化规律(强化准则),依然通过等效塑性应变 ${{\tilde{ \varepsilon }}^{{\rm p}}}$
Yield criterion in plastic-damage models for concrete
3
2010
... 式中: $\tilde\varepsilon^{\rm p} $ x 〉=(|x |+x )/2;I 1 、J 2 分别为第一应力张量不变量和第二偏应力张量不变量; ${{{\bar{{\sigma }}}}_{\max }}$ ${{\bar \sigma }}$ c 为混凝土黏聚力;参数α 、β 由混凝土单轴拉压强度和双轴等压强度确定,具体过程可参见文献[26 ];在文献[25 ]、[26 ]中,参数γ 通过拉子午线(tensile meridian, TM)与压子午线(compression meridian, CM)来确定,这种方法对于轴压CFST柱而言,存在着无法避免的缺陷[27 ] ,详细阐述如下. ...
... 由上述分析可以得出,参数γ 同时决定了应力空间的屈服面的开口形状和开口角度,而参数γ 仅与参数K c 有关. 因此,在选取合适的参数K c 来确定屈服面的形状后,就可能使屈服面无法具有合适的开口角度,而开口形状往往对于混凝土的弹塑性计算而言更加重要[27 -28 ] ,这就是Lubliner屈服准则的主要缺陷所在. ...
... 对于轴压圆CFST短柱而言,参数γ 应由tanφ cm 来确定[27 ] . 因核心混凝土处于三向受压,混凝土抗压强度显著提高[28 ] : ...
Investigation into Lubliner yield criterion of concrete for 3D simulation
2
2012
... 由上述分析可以得出,参数γ 同时决定了应力空间的屈服面的开口形状和开口角度,而参数γ 仅与参数K c 有关. 因此,在选取合适的参数K c 来确定屈服面的形状后,就可能使屈服面无法具有合适的开口角度,而开口形状往往对于混凝土的弹塑性计算而言更加重要[27 -28 ] ,这就是Lubliner屈服准则的主要缺陷所在. ...
... 对于轴压圆CFST短柱而言,参数γ 应由tanφ cm 来确定[27 ] . 因核心混凝土处于三向受压,混凝土抗压强度显著提高[28 ] : ...
1
... 由Mohr-Coulomb准则[29 ] 可得 ...
1
... 内摩擦角φ 可按文献[30 ]、[31 ]的方法计算: ...
Identification of material parameters for Drucker-Prager plasticity model for FRP confined cir-cular concrete columns
1
2011
... 内摩擦角φ 可按文献[30 ]、[31 ]的方法计算: ...
Finite element modelling of concrete-filled steel stub columns under axial compression
2
2013
... 准确分析混凝土的塑性变形,关键在于获取合理的膨胀角[32 ] . Wang等[33 ] 研究了超高性能混凝土的塑性膨胀角与环向套箍应力之间的关系,但并未考虑材料损伤演化的影响,显著低估了构件的塑性变形. 本文在文献[33 ]的基础上,考虑材料损伤演化的影响,重新推导膨胀角的计算方法. ...
... 在无可靠试验数据的前提下,可采用文献[32 ]建议的塑性膨胀角计算公式: ...
Constitutive model for confined ultra-high strength concrete in steel tube
2
2016
... 准确分析混凝土的塑性变形,关键在于获取合理的膨胀角[32 ] . Wang等[33 ] 研究了超高性能混凝土的塑性膨胀角与环向套箍应力之间的关系,但并未考虑材料损伤演化的影响,显著低估了构件的塑性变形. 本文在文献[33 ]的基础上,考虑材料损伤演化的影响,重新推导膨胀角的计算方法. ...
... 研究了超高性能混凝土的塑性膨胀角与环向套箍应力之间的关系,但并未考虑材料损伤演化的影响,显著低估了构件的塑性变形. 本文在文献[33 ]的基础上,考虑材料损伤演化的影响,重新推导膨胀角的计算方法. ...
ABAQUS混凝土损伤因子取值方法研究
3
2013
... 式中:d c 的计算方法可参见文献[34 ]. 根据文献[26 ],混凝土的屈服面演化规律(强化准则),依然通过等效塑性应变 ${{\tilde{ \varepsilon }}^{{\rm p}}}$
... 目前关于多轴不同应力水平作用下的徐变规律研究还不成熟,没有直接可供借鉴的预测模型,本文拟通过引入徐变泊松比的概念,把单轴徐变规律拓展到多轴应力状态下,文献[20 ]、[34 ]采用了类似的方法. ...
... 选用ABAQUS软件对试件进行有限元模拟,混凝土和钢管分别采用实体单元C3D8、C3D8I,钢管与混凝土交界面法向采用“硬接触”模拟,切向采用摩擦罚函数模拟,界面摩擦系数取0.25[41 ] . 假定垫板为不变形刚体,垫板与钢和混凝土的连结采用绑定约束. 由于无该试件受压全过程荷载位移曲线实测数据,膨胀角按式(24)进行计算,试验I与试验II试件的膨胀角分别为27.5°与34.1°,其他参数计算参见文献[34 ]. 有限元网格模型如图4 所示. 文献[9 ]与[38 ]的实测应变与分析结果对比如图5 所示,图中T表示试验组. ...
ABAQUS混凝土损伤因子取值方法研究
3
2013
... 式中:d c 的计算方法可参见文献[34 ]. 根据文献[26 ],混凝土的屈服面演化规律(强化准则),依然通过等效塑性应变 ${{\tilde{ \varepsilon }}^{{\rm p}}}$
... 目前关于多轴不同应力水平作用下的徐变规律研究还不成熟,没有直接可供借鉴的预测模型,本文拟通过引入徐变泊松比的概念,把单轴徐变规律拓展到多轴应力状态下,文献[20 ]、[34 ]采用了类似的方法. ...
... 选用ABAQUS软件对试件进行有限元模拟,混凝土和钢管分别采用实体单元C3D8、C3D8I,钢管与混凝土交界面法向采用“硬接触”模拟,切向采用摩擦罚函数模拟,界面摩擦系数取0.25[41 ] . 假定垫板为不变形刚体,垫板与钢和混凝土的连结采用绑定约束. 由于无该试件受压全过程荷载位移曲线实测数据,膨胀角按式(24)进行计算,试验I与试验II试件的膨胀角分别为27.5°与34.1°,其他参数计算参见文献[34 ]. 有限元网格模型如图4 所示. 文献[9 ]与[38 ]的实测应变与分析结果对比如图5 所示,图中T表示试验组. ...
Nonlinear creep, Poisson's ratio, and creep-damage interaction of concrete in compression
1
2002
... 单轴应力下的徐变泊松比是指在轴向应力作用下,横向徐变与轴向徐变之比. 当在多轴应力状态下,不同主应力方向的泊松比μ cp, i 还与应力状态有关[35 -37 ] ,可表达为 ...
1
... 单轴应力下的徐变泊松比是指在轴向应力作用下,横向徐变与轴向徐变之比. 当在多轴应力状态下,不同主应力方向的泊松比μ cp, i 还与应力状态有关[35 -37 ] ,可表达为 ...
3
... 付学宝等[9 , 38 ] 分别进行了不同应力水平作用下的轴压圆CFST短柱徐变试验,为便于描述,简记为试验I与试验II. 各试件尺寸、加载荷载、应力水平等如表1 所示,D 为圆柱体试件外径;T 为钢管厚度;h 为时间高度;F 为试验荷载大小;n c 表示混凝土应力水平,为核心混凝土的初始应力和圆柱体抗压强度平均值之比. ...
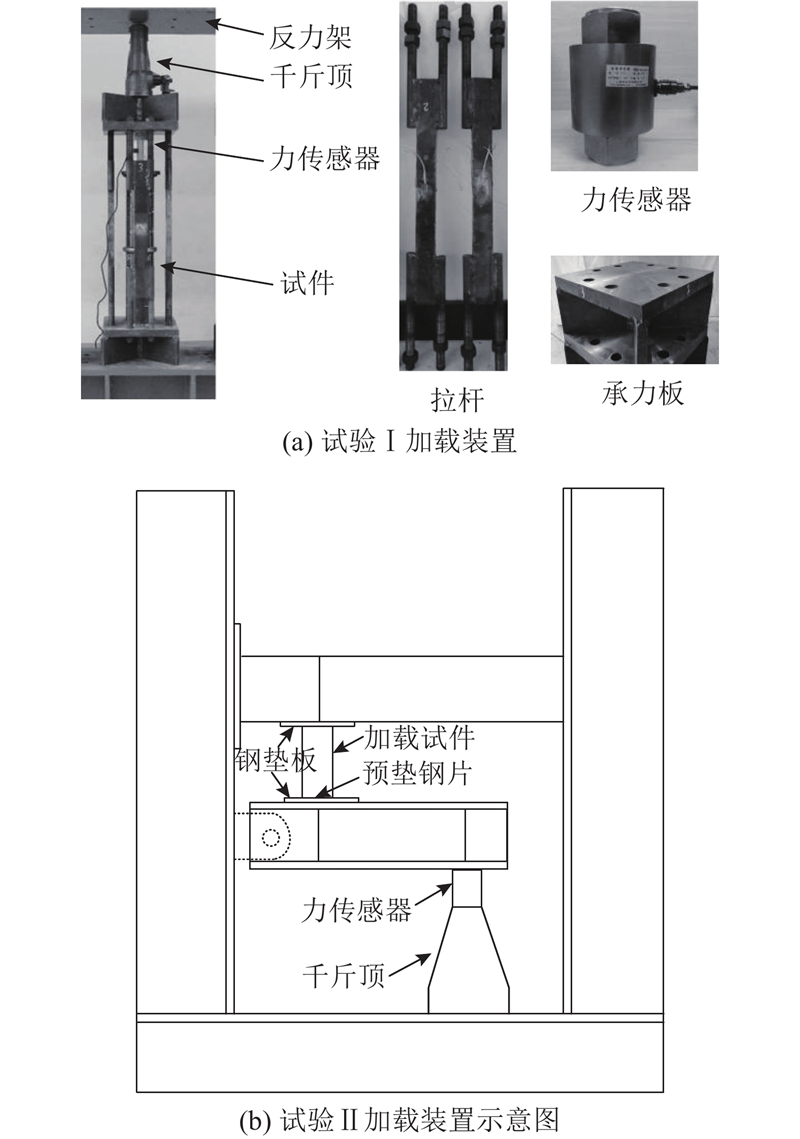
... 核心混凝土和钢管材料参数如表2 所示. f ck 表示Φ 150×300 mm圆柱体试块抗压强度标准值;f y 表示钢管屈服强度;E c 代表混凝土弹性模量,E s 代表钢管弹性模量. 试验在试验室内进行,室内温度相对恒定. 应变测点均位于试件中部. 试验加载方案如图3 所示,均通过千斤顶与力传感器配合加载,当徐变引起的千斤顶卸载超过1%时进行补载. 另外,在文献[38 ]中,为避免杠杆加载引起荷载偏心,在试件底面预垫了薄钢片. ...
... 选用ABAQUS软件对试件进行有限元模拟,混凝土和钢管分别采用实体单元C3D8、C3D8I,钢管与混凝土交界面法向采用“硬接触”模拟,切向采用摩擦罚函数模拟,界面摩擦系数取0.25[41 ] . 假定垫板为不变形刚体,垫板与钢和混凝土的连结采用绑定约束. 由于无该试件受压全过程荷载位移曲线实测数据,膨胀角按式(24)进行计算,试验I与试验II试件的膨胀角分别为27.5°与34.1°,其他参数计算参见文献[34 ]. 有限元网格模型如图4 所示. 文献[9 ]与[38 ]的实测应变与分析结果对比如图5 所示,图中T表示试验组. ...
3
... 付学宝等[9 , 38 ] 分别进行了不同应力水平作用下的轴压圆CFST短柱徐变试验,为便于描述,简记为试验I与试验II. 各试件尺寸、加载荷载、应力水平等如表1 所示,D 为圆柱体试件外径;T 为钢管厚度;h 为时间高度;F 为试验荷载大小;n c 表示混凝土应力水平,为核心混凝土的初始应力和圆柱体抗压强度平均值之比. ...
... 核心混凝土和钢管材料参数如表2 所示. f ck 表示Φ 150×300 mm圆柱体试块抗压强度标准值;f y 表示钢管屈服强度;E c 代表混凝土弹性模量,E s 代表钢管弹性模量. 试验在试验室内进行,室内温度相对恒定. 应变测点均位于试件中部. 试验加载方案如图3 所示,均通过千斤顶与力传感器配合加载,当徐变引起的千斤顶卸载超过1%时进行补载. 另外,在文献[38 ]中,为避免杠杆加载引起荷载偏心,在试件底面预垫了薄钢片. ...
... 选用ABAQUS软件对试件进行有限元模拟,混凝土和钢管分别采用实体单元C3D8、C3D8I,钢管与混凝土交界面法向采用“硬接触”模拟,切向采用摩擦罚函数模拟,界面摩擦系数取0.25[41 ] . 假定垫板为不变形刚体,垫板与钢和混凝土的连结采用绑定约束. 由于无该试件受压全过程荷载位移曲线实测数据,膨胀角按式(24)进行计算,试验I与试验II试件的膨胀角分别为27.5°与34.1°,其他参数计算参见文献[34 ]. 有限元网格模型如图4 所示. 文献[9 ]与[38 ]的实测应变与分析结果对比如图5 所示,图中T表示试验组. ...
Statistical comparisons of creep and shrinkage prediction models using RILEM and NU-ITI databases
1
2015
... 收缩徐变预测模型均选用Bazant教授提出的B4模型,一是因为该模型考虑因素较为全面,具有较高的精度[39 ] ;二是因为该模型把徐变分为干燥徐变与基本徐变,收缩分为干燥收缩与自收缩,而干燥徐变与干燥收缩有关,当不计干燥徐变与干燥收缩时,能够契合CFST基本不与外界发生湿度交换的特殊使用环境. 同时,对于自收缩变形的计算,因为混凝土自生水化反应会消耗一部分水分,混凝土湿度取85%[40 ] . 值得注意的是,数据观测是从28 d龄期开始,而此时自收缩变形已基本完成,因此模型计算结果要剔除自收缩引起的徐变变形后,才能与试验数据对比. ...
Moisture movement in early ages concrete under cement hydration and environmental drying
1
2016
... 收缩徐变预测模型均选用Bazant教授提出的B4模型,一是因为该模型考虑因素较为全面,具有较高的精度[39 ] ;二是因为该模型把徐变分为干燥徐变与基本徐变,收缩分为干燥收缩与自收缩,而干燥徐变与干燥收缩有关,当不计干燥徐变与干燥收缩时,能够契合CFST基本不与外界发生湿度交换的特殊使用环境. 同时,对于自收缩变形的计算,因为混凝土自生水化反应会消耗一部分水分,混凝土湿度取85%[40 ] . 值得注意的是,数据观测是从28 d龄期开始,而此时自收缩变形已基本完成,因此模型计算结果要剔除自收缩引起的徐变变形后,才能与试验数据对比. ...
Numerical analysis of recycled aggregate concrete-filled steel tube stub columns
1
2016
... 选用ABAQUS软件对试件进行有限元模拟,混凝土和钢管分别采用实体单元C3D8、C3D8I,钢管与混凝土交界面法向采用“硬接触”模拟,切向采用摩擦罚函数模拟,界面摩擦系数取0.25[41 ] . 假定垫板为不变形刚体,垫板与钢和混凝土的连结采用绑定约束. 由于无该试件受压全过程荷载位移曲线实测数据,膨胀角按式(24)进行计算,试验I与试验II试件的膨胀角分别为27.5°与34.1°,其他参数计算参见文献[34 ]. 有限元网格模型如图4 所示. 文献[9 ]与[38 ]的实测应变与分析结果对比如图5 所示,图中T表示试验组. ...