随着高速公路、铁路不断提速以及城市地铁、高架桥等各种基础设施的不断完善,交通荷载引发的地基振动问题日益突出,更加引起社会各界的关注。尤其是我国东部、南部等沿海地区广泛分布着含水率高、承载能力低、模量低、易发生较大沉降的软黏土,在交通荷载作用下易产生过大地基振动,影响道路服役性能及旅客乘车安全。
早在20世纪50年代,Sneddon等[1-2]率先对匀速移动荷载作用下的弹性半空间动力响应问题展开研究,首次将Fourier变换应用于求解该问题,并得到积分解。Eason [3]采用积分变换法,针对匀速移动荷载作用下半无限均质各向同性弹性介质的位移与动应力响应问题进行了研究。以上研究的共同点是采用单相弹性介质模拟地基土体,忽略天然土体中存在的孔隙水,因此从该角度而言,饱和半空间土体模型与单相弹性土体模型相比具有明显的优势。Biot作为饱和土动力学理论的奠基者,率先提出动力控制方程,并将地基模拟为饱和多孔弹性介质[4-5]。Siddharthan等[6]通过近似求解Biot动力方程,研究了成层半空间土体的动力响应。Cai等[7]研究了移动矩形荷载作用下,饱和半空间土体动力响应的三维问题,通过半解析法详细分析了荷载移动速度、土体渗透系数等因素对土体位移、加速度、超静孔压等动力响应的影响。蔡袁强等[8]采用半解析法研究了移动条形荷载作用下上覆弹性板饱和两相介质的动力响应问题,分析表明弹性梁刚度会较大程度地影响地基位移和孔压等响应。Cai等[9]采用解析法研究了交通荷载作用下饱和半空间上覆路面系统的动力响应,得到了路面-地基系统的振动速度及动应力分布。通过建立三维道路系统模型,曹志刚等[10]采用半解析法研究了车辆荷载作用下高速公路的动力响应问题,经数值计算发现荷载移动速度、土体渗透系数以及板的刚度是影响道路系统位移响应的主要因素。Ai等[11]考虑了横向各向同性、介质厚度、分层特性、加载速度和荷载深度等影响因素,开展了移动荷载作用下横观各向同性多层介质的动力响应研究,结果表明垂直位移随介质厚度的增加而增大。Feng等[12]采用三维半解析方法针对具有软弱饱和夹层的成层地基动力响应开展研究,研究表明饱和夹层的渗透性和边界条件对孔隙压力的分布产生影响,且夹层厚度对地基谐振频率影响较大。
在实际工况中,不平顺路面会明显加剧交通荷载产生的地基振动,给路面结构带来附加破坏,严重影响道路服役性能。以上文献未考虑不平顺路面这一因素。Cai等[13]研究了交通荷载作用下不平顺路面-饱和地基系统的动力响应,详细分析了由车辆轴重荷载和不平顺路面产生的动力荷载引起的饱和地基土体中的应力和孔隙水压响应,并绘制了土体单元总应力路径和有效应力路径图。Liu等[14]采用移动单元法研究高速列车荷载作用下饱和地基表层的动力响应,并详细讨论了列车速度、弹性模量、土体渗透性、铁路不平顺、透水边界等因素的影响。Qian等[15]采用Fourier积分变换和传播矩阵法求解了在不平顺路面引发的车辆动力荷载作用下饱和多孔半空间的三维动应力解析解,研究表明在车速较低及土体刚度较大工况下,车辆动力荷载会对地基动应力响应产生较大影响。
一般而言,各层土体性质截然不同的成层地基比均匀地基更符合实际工程情况。地基土体的变化结合不平顺路面引发的车轮-路面动力荷载的作用,会引起地基振动响应特性发生显著改变,而目前缺乏此类研究。因此,有必要开展不平顺路面对交通荷载引起的成层地基振动影响研究。
通过建立交通荷载-不平顺路面-双层地基耦合模型,本文主要研究不平顺路面对高速交通荷载引起的成层地基振动的影响。交通荷载分为车辆自身轴重荷载与不平顺路面引发的车轮-路面相互作用动力荷载。采用Kirchhoff薄板理论模拟路面系统,采用单相弹性介质理论与Biot饱和两相介质理论模拟地基上、下层土体。通过Fourier变换求解控制方程,分析并对比轴重荷载和动力荷载对成层地基土体竖向加速度、竖向动应力及超静孔压响应的影响。
1. 模型建立
所建立的交通荷载-不平顺路面-双层地基耦合模型,如图1所示,
图 1
图 1 交通荷载-不平顺路面-双层地基耦合模型
Fig.1 Traffic load-uneven pavement-double-layered ground coupling model
忽略土颗粒的压缩性及土体自重,地基下层土体采用Biot[5]提出的饱和土体控制方程:
饱和土体本构关系为
式中:
忽略土体自重的线弹性介质动力方程为
式中:上、下标e表示弹性介质(elastic medium),
土体的应力、应变关系为
式中:
用Kirchhoff薄板理论来描述刚性路面系统,其控制微分方程[16]为
式中:
其中,
假设薄板与弹性地基土体之间为光滑接触条件,则
假设弹性层与饱和半空间之间为透水边界,则弹性土体与饱和半空间土体之间的边界条件(
车辆运动微分方程[18]为
式中:
车辆轮对和路面之间的弹簧与阻尼器可视为Hertzian接触弹簧[19],其刚度为
其中,i为虚数单位,
式中:不平顺路面幅值A=10 mm,波长λ0=0.8~333.3 m.
假设车轮与路面始终保持接触,则依据式(24)可求得不平顺路面引发的车轮-路面动力荷载
式中:
定义对时间
由以上分析可知,交通荷载作用下,成层地基中的上层弹性土体与下层饱和土体的竖向正应力表达式分别为
式中:
2. 数值计算分析
表 1 交通荷载-不平顺路面-双层地基耦合模型中的交通荷载参数
Tab.1
| 车辆整体参数 | 车轮与转向架参数 | |||||||
| | | | | | | | | |
| 404.36 | 4.15 | 0.32×0.22 | 0.50×0.35 | 2 060 000 | 370 000 | 900 | 600 | |
表 2 交通荷载-不平顺路面-双层地基耦合模型中的地基土层参数
Tab.2
| 弹性土体参数 | 饱和土体参数 | |||||||||
| | | | | | | | | | | |
| 1×106~1×108 | 2 | 1 089.6 | 0.35 | 1×107 | 1816 | 0.4 | 0.35 | 1.2×108 | 1.22×106 | |
式中:
2.1. 模型验证
图 2
图 2 土体竖向正应力与剪切应力计算结果与已有文献的对比
Fig.2 Comparisons of soil vertical normal stress and shear stress between present work and existing work
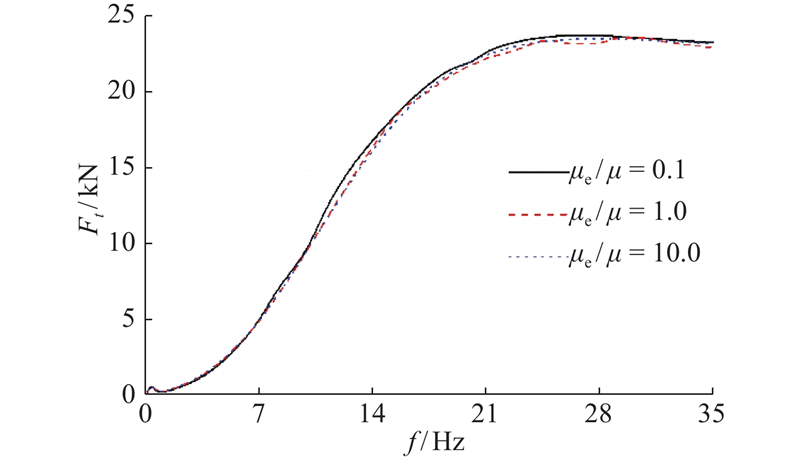
2.2. 车轮-路面动力荷载随激振频率的变化
将交通荷载分为两部分:车辆因自身轴重引发的荷载(简称“轴重荷载”)与不平顺路面引发的车轮-路面相互作用动力荷载(简称“动力荷载”).在本文所有算例中,车辆质心初始位置均位于
图 3
图 3 车轮-路面动力荷载随激振频率的变化
Fig.3 Changes of wheel-pavement dynamic loading against excitation frequency.
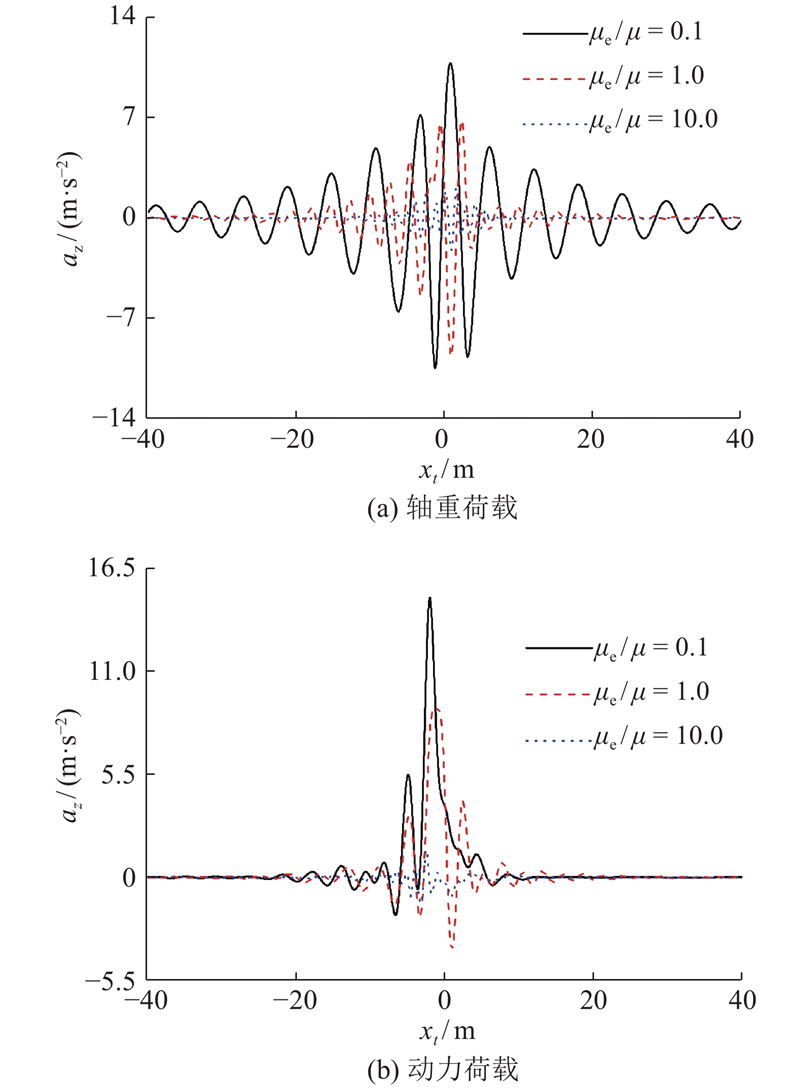
2.3. 交通荷载对地基土体竖向加速度的影响
图 4
图 4
地基
Fig.4
Time-history curves for vertical acceleration of subsoil at position of
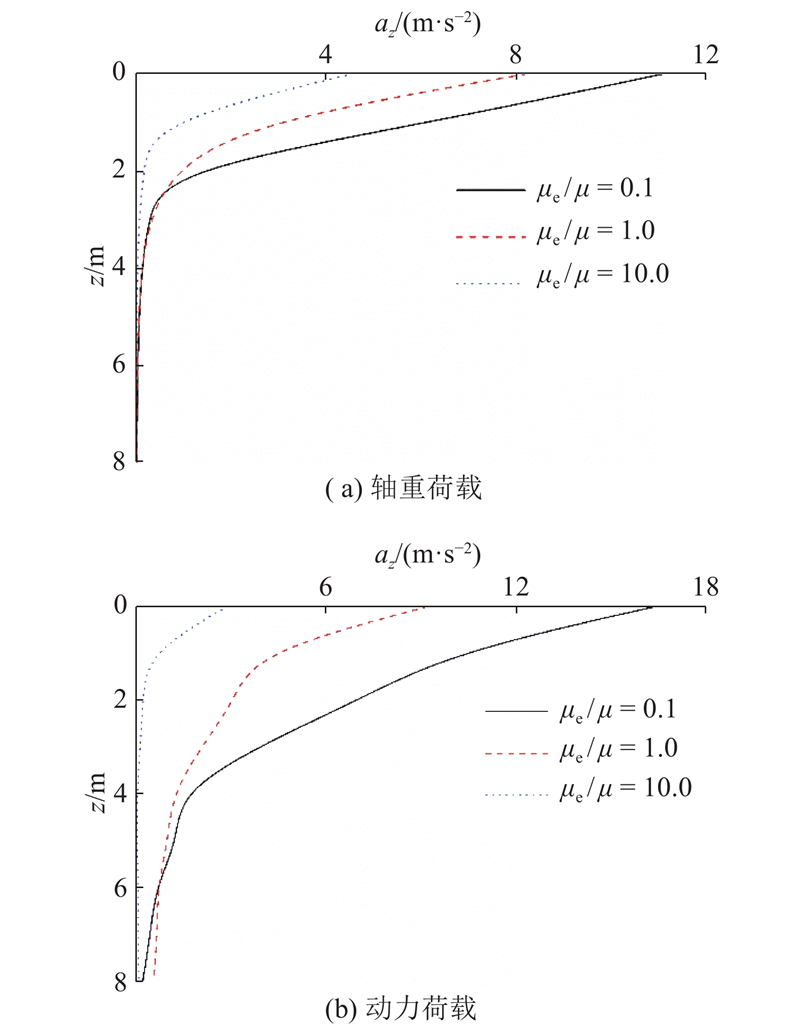
图 5
图 5 地基土体竖向加速度响应随地基深度的变化
Fig.5 Changes of subsoil vertical acceleration responses against ground depths
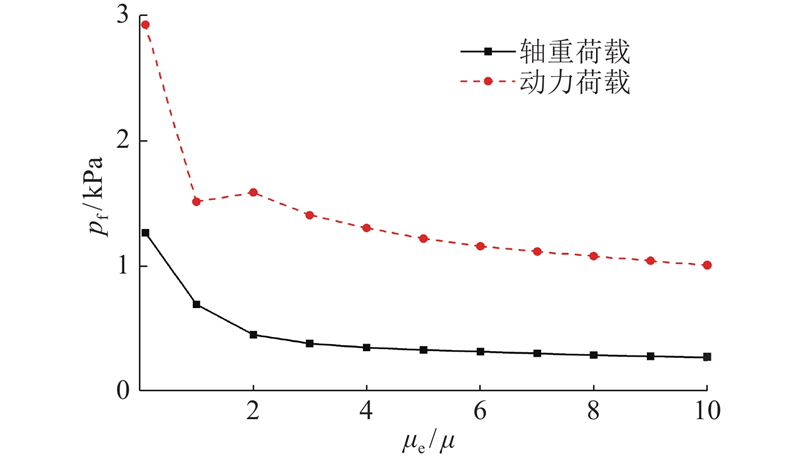
如图6所示为地基表层土体在轴重荷载和动力荷载作用下的竖向加速度(
图 6
图 6 地基表层土体竖向加速度响应随地基上、下层土体剪切模量之比的变化
Fig.6 Change for vertical acceleration responses of surface subsoil against ratio of shear modulus of upper and lower soil
2.4. 交通荷载对地基土体竖向正应力的影响
图 7
图 7
地基
Fig.7
Time-history curves for vertical stress of subsoil at position of
图 8
图 8 地基土体竖向正应力响应随地基深度的变化
Fig.8 Changes of subsoil vertical stress responses against ground depths
如图9所示为地基表层土体在轴重荷载和动力荷载作用下的竖向正应力(
图 9
图 9 地基表层土体竖向正应力响应随地基上、下层土体剪切模量之比的变化
Fig.9 Changes for vertical stress responses of surface subsoil against ratio of shear modulus of upper and lower soil
2.5. 交通荷载对地基饱和土体超静孔压的影响
图 10
图 10 地基饱和土体超静孔压响应随地基深度的变化
Fig.10 Changes of excess pore water pressure responses of saturated subsoil against ground depths
图 11
图 11
地基
Fig.11 Changes of excess pore water pressure of the subsoil at depth of 2.5 m against ratio of shear modulus of upper and lower soil
3. 结 论
(1)地基表层土体的竖向加速度响应随地基上、下层土体剪切模量之比增大而减小;当上层土体模量较小时,动力荷载对地表加速度响应贡献较大;当上层土体模量增大后,轴重荷载引起的振动响应更大,但动力荷载影响仍不可忽略。
(2)地基表层土体的竖向正应力响应随
(3)交通荷载作用下地基土体竖向加速度与竖向正应力响应随地基深度快速衰减,在地基深度3 m以下范围动力响应趋于稳定。
(4)交通荷载作用下饱和地基超静孔隙水压随上、下层土体剪切模量之比的增大而减小,且动力荷载引发的饱和地基超静孔隙水压大于轴重荷载,可见动力荷载对饱和地基超静孔压响应的影响极大。
参考文献
The stress produced by a pulse of pressure moving along the surface of a semi-infinite solid
[J].DOI:10.1007/BF02843720 [本文引用: 1]
The stresses produced in a semi-infinite solid by a moving surface force
[J].DOI:10.1016/0020-7225(65)90038-8 [本文引用: 1]
Mechanics of deformation and acoustic propagation in porous media
[J].DOI:10.1063/1.1728759 [本文引用: 1]
Theory of propagation of elastic waves in a fluid saturated porous solid. I. Low frequency range
[J].DOI:10.1121/1.1908239 [本文引用: 2]
Moving load response of layered soil. I: Formulation; Ⅱ: Verification and application
[J].DOI:10.1061/(ASCE)0733-9399(1993)119:10(2052) [本文引用: 2]
Steady state responses of poroelastic half-space soil medium to a moving rectangular load
[J].
移动荷载下上覆弹性板饱和地基的动力响应
[J].
Response of beams on poroelastic half-space soil medium to moving load
[J].
Dynamic response of pavements on poroelastic half-space soil medium to a moving traffic load
[J].
移动车辆荷载作用下路面的动力响应
[J].
Dynamic response of pavement subjected to moving traffic load
[J].
3D dynamic response of a transversely isotropic multilayered medium subjected to a moving load
[J].DOI:10.1002/nag.v42.4 [本文引用: 1]
Three‐dimensional dynamic response of ground with a poroviscoelastic interlayer to a harmonic moving rectangular load
[J].DOI:10.1002/nag.v41.7 [本文引用: 1]
Dynamic responses of a saturated poroelastic half-space generated by a moving truck on the uneven pavement
[J].DOI:10.1016/j.soildyn.2014.10.014 [本文引用: 2]
Dynamic response of water saturated subgrade surface layer under high speed train using moving element method
[J].DOI:10.21595/jve.2017.18187 [本文引用: 1]
Influence of pavement roughness on dynamic stresses in saturated subsoil subjected to moving traffic loading
[J].DOI:10.1061/(ASCE)GM.1943-5622.0001097 [本文引用: 1]
Dynamic response of plate on viscous Winkler foundation to moving loads of varying amplitude
[J].DOI:10.1016/S0141-0296(03)00066-X [本文引用: 2]
Three‐dimensional steady‐state response of a railway system on layered half‐space soil medium subjected to a moving train
[J].DOI:10.1002/nag.v33:4 [本文引用: 1]
An efficient algorithm for dynamic analysis of bridges under moving vehicles using a coupled modal and physical components approach
[J].DOI:10.1006/jsvi.1997.1459 [本文引用: 1]
Normal vibrations and friction under harmonic loads: Part I—Hertzian contacts
[J].DOI:10.1115/1.2920607 [本文引用: 1]
Dynamic responses of a poroelastic half-space from moving trains caused by vertical track irregularities
[J].DOI:10.1002/nag.v35.7 [本文引用: 1]
Surface vibration due to a sequence of high speed moving harmonic rectangular loads
[J].DOI:10.1016/S0267-7261(02)00034-9 [本文引用: 1]
重型汽车荷载作用下简支梁桥的动力反应分析
[J].DOI:10.3969/j.issn.1674-0610.2005.02.016 [本文引用: 1]
Analysis of dynamic responses of simply supported girder bridge under heavy moving vehicles
[J].DOI:10.3969/j.issn.1674-0610.2005.02.016 [本文引用: 1]
A half-space saturated poro-elastic medium subjected to a moving point load
[J].DOI:10.1016/j.ijsolstr.2006.05.020 [本文引用: 3]