薄壳在包括土木建筑、航天航空、机械电子等在内的工程科技领域有着广泛应用,如穹顶、航天器、舰艇以及工业设备与产品的外壳等. 壳体造型多为复杂曲面,受力后将同时发生面内位移和横向位移,整体的薄膜状态和弯曲状态相互耦合,需要同时分析,这使得薄壳的力学求解通常比较复杂. 早期均通过建立微分方程来获得其解析解[1],但面对非线性问题时就非常困难,因而目前主要是根据虚功或能量变分原理建立弱形式的等效积分方程,并借助数值方法来求出一组离散解. 但面对实际工程中不断出现的一些复杂动力问题,尤其是同时涉及到壳体结构的大变形、大转动、屈曲、碰撞、破坏等高度非线性的力学行为时,许多传统方法常由于计算量和数值稳定等方面的局限性而求解困难[2-3]. 因此,亟需发展力学描述与计算列式更为简洁且能够有效处理薄壳动力强非线性问题的数值分析方法.
有限单元法是当前薄壳非线性分析中最常用的数值方法. 依据不同的几何描述、壳体理论、插值函数及各异的处理技巧,已开发了诸多有限元列式,大致可将其分为两类[4]:一类是直接建立于壳体理论平衡方程的等效积分弱形式,如DKT单元[5]、BWC单元[6]、BST单元[7]、ANCF单元[8]、IGAS单元[9]等;另一类是通过在连续体单元上强制引入壳体理论的运动假设建立壳单元(即基于连续体(CB)的壳),如MITC4单元[10]、HL单元[11]等. 对于前者,当涉及到非线性问题时,由于理论上的限制,要建立与壳单元变分弱形式等效的控制方程会有本质上的困难;而后者通过CB方法建立壳单元离散方程,比较直观,适用于任意壳体的大变形问题,但由于采用的是等效R-M运动假设,可能出现剪切和薄膜自锁现象,需要引入设置缩减积分或假设应变场等特殊技巧才能够完成分析[12].
有别于传统分析力学架构下的计算方法,有限质点法是基于向量式力学理论提出的面向工程结构复杂行为的新型数值分析方法[13]. 该方法采取多质点离散的物理分析模式,根据牛顿定律通过追踪质点的运动轨迹来获得结构整体的运动和变形情况,动力和几何非线性描述是该方法的本质特征;各质点运动方程相互独立,不涉及刚度矩阵的集成和求逆,也不需要迭代求解,避免了方程病态或刚度矩阵奇异而造成的数值求解困难,在结构复杂非线性问题分析中具有优势和灵活性. 目前该方法已被应用于机构运动、接触碰撞、结构屈曲、倒塌破坏、固体大变形、膜结构找形、结构多尺度精细化等结构复杂行为的分析[14-15],均取得了较好的效果. 同时,有许多学者同样基于向量式力学和数值计算相结合的概念发展了向量式有限元方法[16],开发了包括DKT壳单元在内的众多类型单元,对薄壳的弹塑性本构、碰撞和穿透等问题进行了初步研究[17-18].
本文将通过理论推导、程序编制及算例,进一步发展通用的有限质点法薄壳动力非线性行为的分析框架,完善此类方法的计算理论体系. 首先介绍薄壳的有限质点法基本理论和控制方程,推导有限质点法处理薄壳纯变形和质点内力(矩)计算公式;然后根据有限质点法的计算特点对薄壳质点的转动惯量、时间步长和阻尼等关键参数取值及质点控制方程的数值求解提出合理可行的处理策略;同时利用经典的J2流动理论处理薄壳平面应力弹塑性问题,建立算法的具体实现步骤;最后通过算例的模拟和分析,检验方法的正确性和有效性.
1. 有限质点法薄壳计算理论
有限质点法采用标准化向量式力学分析架构,可同时求解结构体系受力后的位置变化与几何变形,其基本概念包括:1)点值描述;2)途径单元;3)刚体运动和纯变形分离的物理模式处理;4)基于牛顿第二定律的强形式广义质点运动控制方程. 关于有限质点法的基本思想详见文献[13],这里结合薄壳理论仅简单介绍其要点.
1.1. 离散质点模型
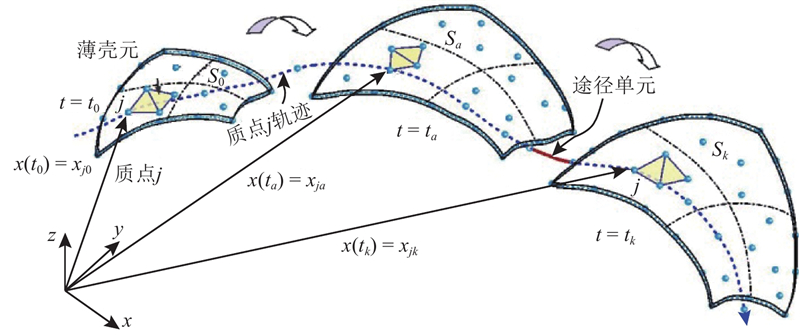
薄壳属于退化三维固体模型,应同时考虑薄膜刚度和弯曲刚度的影响. 有限质点法将薄壳离散为一组具有空间平动与转动自由度的质点集合,质点间由一系列具备描述面内外变形能力的薄壳元相连. 薄壳中所有物理量均由各个质点的点值描述. 薄壳元没有质量,仅用于表示质点间相互作用,随质点运动发生变形,由此产生的内力反作用于相连质点.
如图1所示,假设一薄壳构件经历一个连续变形和运动过程,从初始时刻t0的构形S0经中间时刻(
图 1
图 1 薄壳离散质点群模型及任一质点的运动情况
Fig.1 Shell model built by discrete particles group and motion of arbitrary particle
1.2. 质点运动方程
有限质点法从物理角度考虑,认为所有质点均处于动平衡状态,在每个途径单元(如ta≤t≤tb)内的运动都遵循牛顿第二定律,且控制方程独立. 薄壳中的质点运动是广义的,对于壳面上任一质点j,其运动变量包括沿坐标轴方向的3个平动自由度和绕轴旋转的3个转动自由度,对应3个坐标方向的质点力和力矩,因此薄壳质点运动控制方程式可分为点的平动公式和点的转角公式. 前者用于求解中面内变形引起的质点位置改变(可直接利用薄膜质点空间运动方程[19]进行求解),后者用于求解面外弯曲变形引起的质点截面转动.
根据经典薄壳理论,质点截面转动只产生弯曲变形而没有壳面内扭转,因此需要转换到质点的切平面坐标系下建立其转动控制方程. 如图2所示,令坐标平面
图 2
图 2 质点转动计算的局部切平面坐标系
Fig.2 Local tangent plane of a particle for rotation calculation
式中:
其中,
质点内力矩来自于质点转动引起的壳元弯曲变形,可通过其相连壳元的节点等效内力矩
式中:nc为质点j相连薄壳元个数.
质点外力矩包括作用在质点上的集中力矩
阻尼力矩可写成瑞利比例阻尼的形式根据壳体黏滞特性计算:
其中,质量阻尼力矩
Ij为质点j在全域坐标系下的惯性矩阵;刚度阻尼力矩
其中,am和as为阻尼参数,
绕
式中:Nj为质点j相邻质点数;
式中:
1.3. 质点内力计算推导
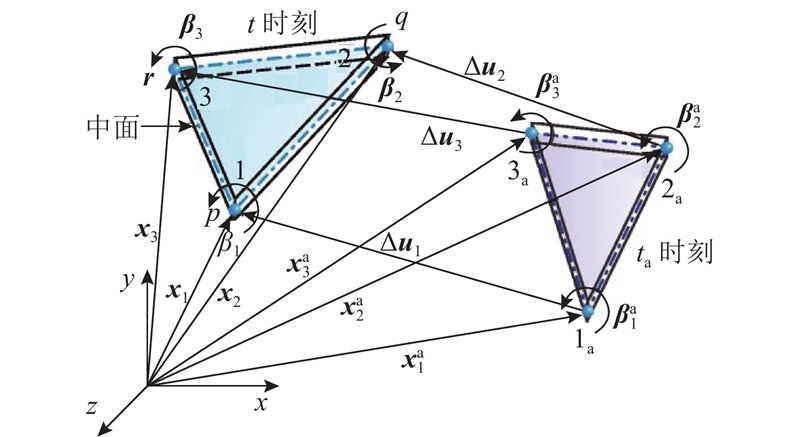
如图3所示,三节点薄壳元(厚度为h)的空间位置和几何构形由位于中面内的3个节点(编号i=1,2,3)确定,每个节点包含3个平动自由度和3个转动自由度. 节点(i=1,2,3)与质点(I=p,q,r)刚性联结,ta和t时刻节点位置向量和转动向量分别记作
图 3
图 3 三节点薄壳元的空间运动描述
Fig.3 Description of spatial motion of three-node shell element
壳面质点内力(矩)仅与相连壳元的纯变形相关,所涉及到的应变、应力物理量均通过节点的纯变形量计算,因此需要对Δui和
式中:ηi和
与传统有限元法不同,式(4)~(6)求出的节点变量是变形位移而非全位移. 内插函数包含刚体模式,将其用于描述薄壳元内的变形分布时,需要将对应于刚体运动模式自由度的3个多余节点变量舍去. 薄壳元经历逆向刚体运动后,处于虚拟位置上的各个节点与ta时刻基础架构位置共面,因此与弯曲元刚体模式相关的3个面外位移分量已被完全扣除,剩下的节点变形转角分量均为独立变量. 为了与膜元部分合算内力,这里仍参照T3薄膜元的处理方式,在壳元基础架构上定义一组变形坐标
令
对于
另外2个变形坐标方向上的刚体转动分量则由θop转换而来,即
于是,式(7)中节点变形转角分量可具体表示如下:
遵循经典板壳理论不考虑面内扭转刚度的基本假设,计算中可忽略
1)
2) 绕
为了描述壳元内的变形和应力,引入传统有限元中的BCIZ平板元形函数作为内插函数,但节点变量仅考虑6个独立转角量
式中:
根据途径单元内小变形假设,应力和应变可采用工程应力和微应变形式,无需引用复杂应力率和应变率公式,本构关系可由材料试验直接给出. 利用
式中:
式中:
不考虑
式中:Aa为ta时刻的薄壳元面积,ha为ta时刻的薄壳元厚度.
虽然这里内力求解过程中不生成刚度矩阵而无法直接计算刚度阻尼,但考虑到刚度阻尼本质上源于材料黏性效应[21],因此阻尼力(矩)也可作为附加内力(矩)通过等效积分来计算得到,即
式(14)、(15)中应力、应变均随位置变化,直接积分较为不便,可借助数值方法进行求解. 对于弹性和弹塑性问题,可分别采用沿厚度方向的2点Gauss积分方案和5点Labatto积分方案,中面内则分别采用三角形3点和7点高斯积分方案.
式(12)和(13)只能求出部分节点力分量
上述薄壳面内、外变形内力的等效节点力
最后,按照薄壳元节点与质点的对应关系,将上述fi和mi反组集到节点i所连接的质点上.
2. 关键参数取值
2.1. 质点广义质量
如上文所述,薄壳所有质量均由质点承担,要求离散质点的质量分布收敛于实际情况. 与变形相对应,薄壳质点的广义质量有两部分,即点的平动质量Mj和转动惯量Ij. 前者的计算与薄膜质点质量的计算方法相同[19];后者把质点视为具有一定形状的均布质量截面,通过组集质点及其相连壳元均匀分配的等效转动惯量得到,即
等效转动惯量
图 4
惯性力矩的转动虚功可表示为
式中:
由此可得局部坐标系下节点1的截面等效转动惯量矩阵为
式中:
2.2. 临界步长与时间积分
有限质点法采用显式直接积分法求解运动方程,以避免复杂迭代和收敛问题. 考虑数值稳定与物理精度两方面约束以及冲击振动中材料变形的影响,本文采用变时间步长法[4],其临界步长满足
式中:
其中,E、ν和ρ分别为材料的弹性模量、泊松比和密度;
其中,As为壳元面积,Li(i=1,2,3)为边长.
利用中央差分格式,可将质点的速度和加速度写成位移和时间的表达式,代入式(1)后可得各时间步质点j切平面内沿独立转动自由度方向的转角和转速分别为(为表示方便,省略下标j)
式中:
实际计算中为保证一定余量,将初始步长Δt0在临界步长基础上折减,即
2.3. 阻尼系数
根据瑞利比例阻尼的定义知阻尼比ξi与圆频率ωi的关系[4]:
对于固定的阻尼比值,am和as是随频率变化的. 作为一种近似,通常可由所关心频率范围上、下限的阻尼比(一般由实验方法或经验确定),根据式(21)得到联立方程定出am和as,作为该频率段的系数使用. 需要指出,ωi的选取与主导振频有关,对于多数低频响应占主导的动力学问题,计算时可只取最低几阶频率范围,而对于冲击等问题则必须考虑激发的高频响应,具体取值可通过结构自由振动数值模拟试验确定. 另外,刚度阻尼主要对高频起作用,而且若as过大,临界步长会大大缩短,因此对于低频动力问题也可忽略刚度阻尼而通过适当提高am方式来考虑总阻尼力或阻尼力矩中as的影响.
3. 材料非线性问题
基于经典J2塑性理论[22],讨论平面应力回退映射算法及其在本文方法中的实现步骤.
3.1. 应力修正
为满足壳面内平面应力状态的限制条件,特别构建应力和应变二维子空间,相应的应力、应变矢量可表示为
根据J2理论流动准则和硬化律,利用向后Euler差分法可得t时刻塑性回退映射各状态量如下:
式中:
将式(22)~(24)代入本构方程
可得到如下参量更新公式:
式中:
由式(22)~(26)可知,各状态量的塑性修正值均取决于
式中:
由于
式中:U为正交矩阵,
式中:
式(28)可利用Newton法局部迭代求解得到
3.2. 算法步骤
上述基于平面应力J2流动理论的塑性应力更新算法在本文方法中的具体实现步骤如下.
1)由各积分点ta−t时段内的平面应变增量
2)将t时刻的应力
若
3)利用回退映射算法的应力修正过程如下.
a)设迭代初始值:i=0,
b)在第i次迭代时由式(27)检查屈服条件,如果函数值
c)利用式(28)由
计算塑性流动因子
d)将
4)更新当前时刻的状态量:
本文方法的质点控制方程内力项(
4. 程序编制及算例
基于前文理论计算公式推导及相关参数的取值策略,同时引入弹塑性应力修正的处理,采用C++语言在Visual Studio平台实现计算分析程序的编写和运行.
整个有限质点法分析程序的实现流程分成前处理、计算求解和后处理. 前处理包括结构模型信息读入(如位置、材料、几何等)和初始分析参数设置(如步长、约束等). 后处理主要是输出计算结果. 求解部分由2层循环构成:外层按时间步循环,内层包含点值循环和单元循环. 点值循环调用该步的内、外力(矩)和阻尼力(矩)等信息采用显式积分求解运动方程获得并更新质点位移(转角)和速度(转速);单元循环通过虚拟运动计算壳元纯变形并获得内力(矩),然后集成到相对应的质点上,并把结果返回给点值循环供下一步质点运动方程积分计算使用. 材料非线性等特殊情况处理可在内层循环中作为单独的计算模块接入,在每次循环中对单元或质点状态作判断,然后调用相应模块. 下面通过若干典型算例分析验证理论推导和所编制程序的有效性和正确性.
4.1. 扁球壳受突加均布面荷载作用
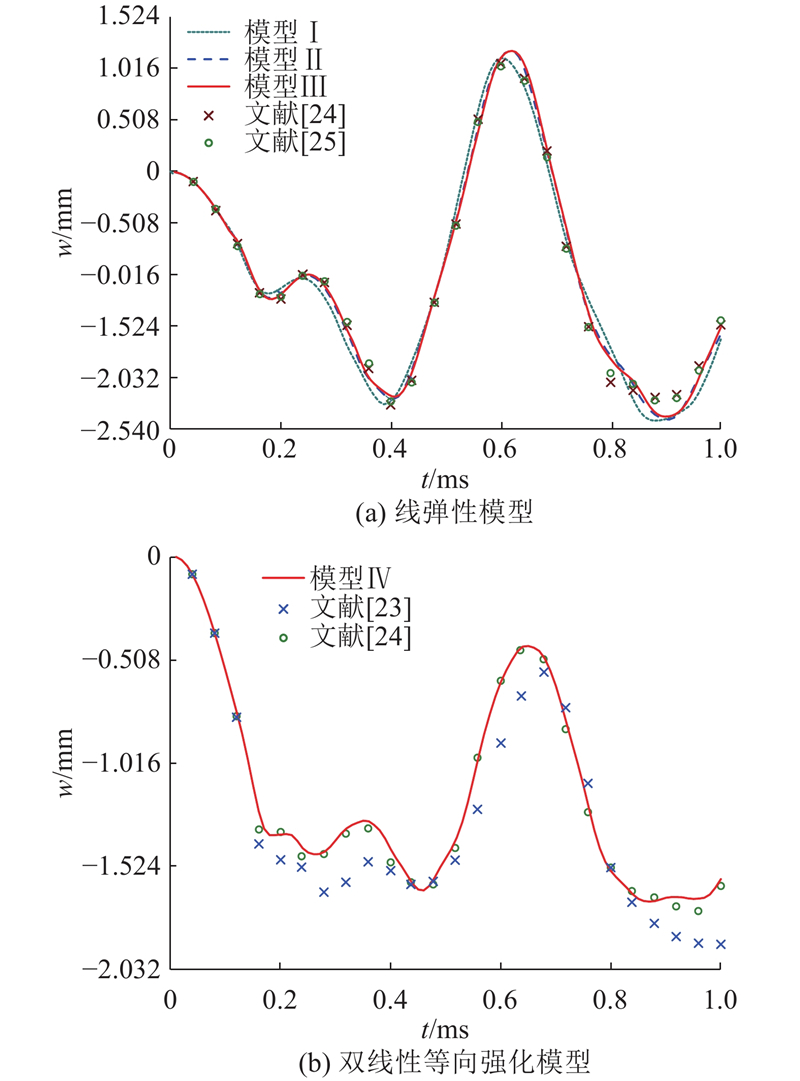
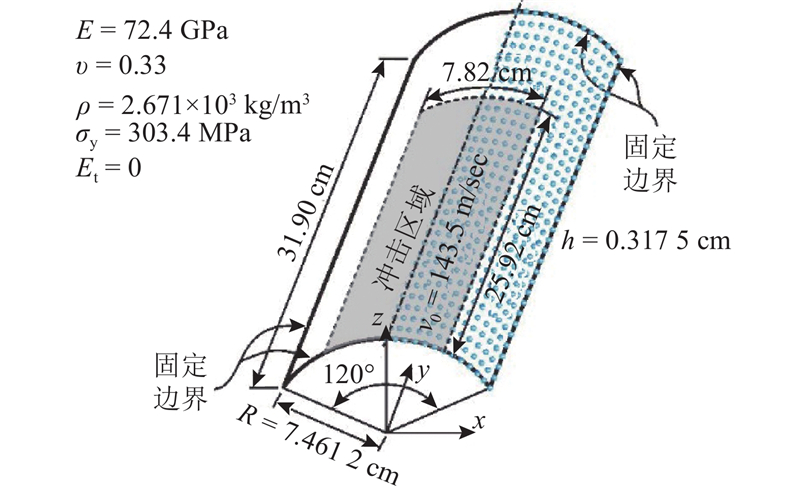
受持续均布压力作用的扁球壳结构是传统薄壳非线性分析中的经典算例[23],常用来验证算法的正确性. 扁球壳周边固定约束,从t=0时刻起,上表面施加恒定均布荷载p=6.137 MPa(为方便与文献对比,这里采用英制单位),作用时间为1 ms,不考虑阻尼效应. 几何尺寸、约束条件、材料性质及受力情况如图5所示. 图中,R为扁球壳半径,α为弧度,h为厚度,E为材料弹性模量,v为泊松比,ρ为密度,σy为屈服应力,Et为切线模量。利用对称性条件,只取1/4部分进行计算. 壳体材料模型考虑线弹性和双线性等向强化弹塑性2种情况. 采用质点数分别为127、469和631的3种离散模型(记作模型Ⅰ ~ Ⅲ,见图6)进行计算,检验算法的收敛性.
图 5
图 5 扁球壳模型:几何、边界及材料性质
Fig.5 Geometry, constraints and material of spherical dome
图 6
图 7
图 7 扁球壳受突加均布荷载作用下的顶点竖向位移时程
Fig.7 History of central deflection of spherical dome under impulse pressure
表 1 扁球壳中心顶点处的竖向位移比较
Tab.1
4.2. 柱面曲壳受瞬时冲击作用
图 8
图 8 受冲击作用柱面曲壳:几何、材料与载荷作用
Fig.8 Geometry, material and loading condition of cylindrical panel under impulse loading
图 9
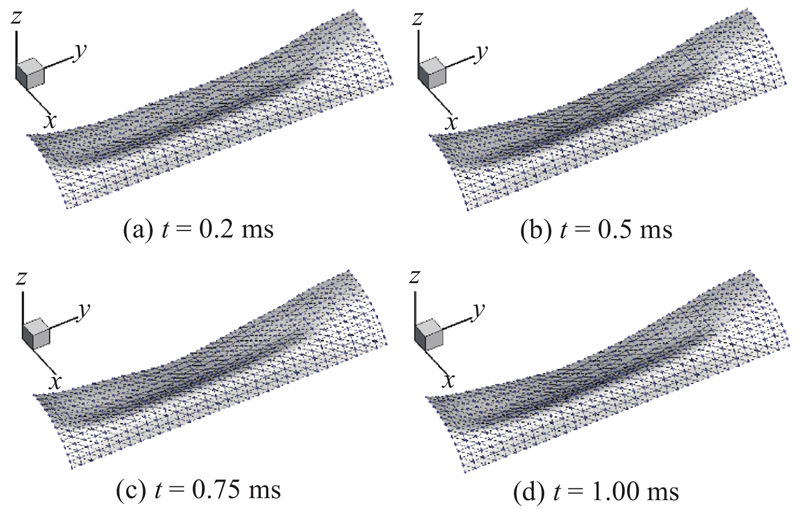
图 9 受冲击后不同时刻的柱面壳形态
Fig.9 Snap shots of cylindrical panel motion after impacting
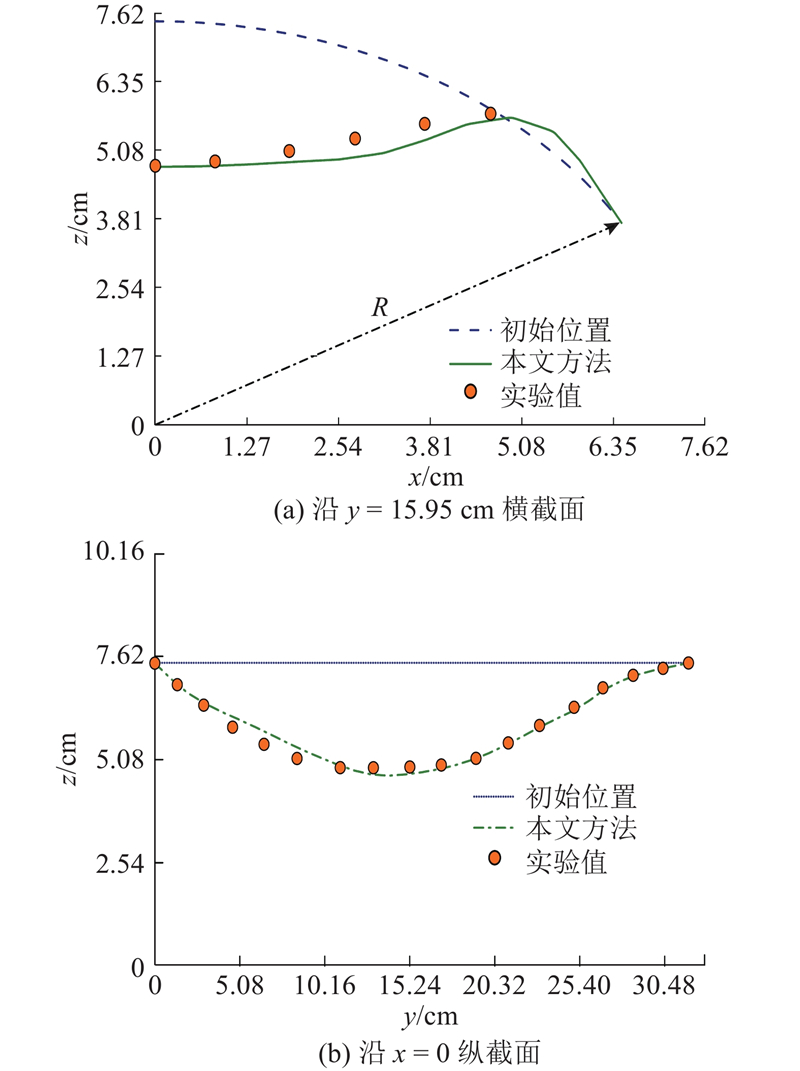
图 10
图 10 柱面曲壳的最终剖面形状与试验结果比较(t=1.0 ms)
Fig.10 Final profiles of panel at time of 1.0 ms obtained from proposed method and experimentally
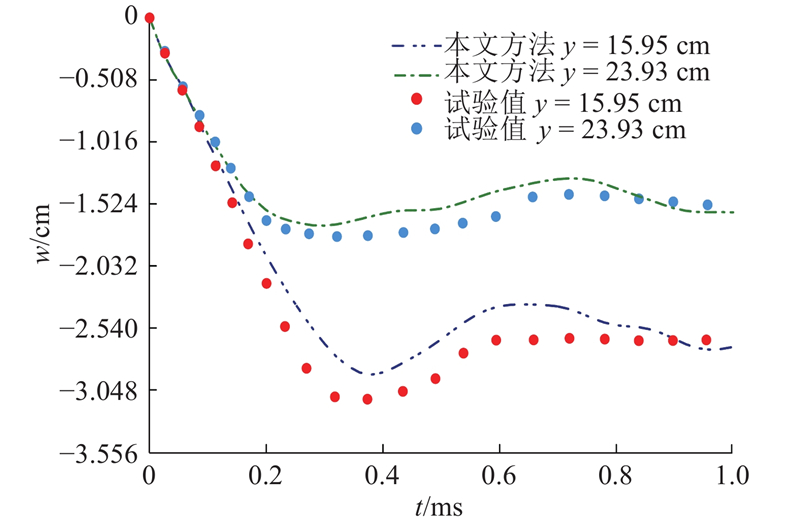
图 11
图 11 柱面曲壳纵轴线上位于y=15.95 cm和y=23.93 cm两点的竖向位移时程曲线
Fig.11 Time history curves of vertical displacements for two points at y=15.95 cm and y=23.93 cm along longitudinal axis
4.3. 薄壁方管受轴向撞击作用
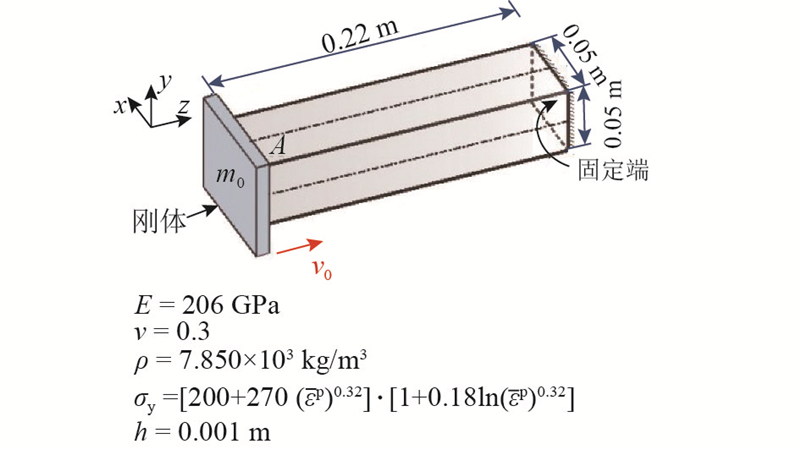
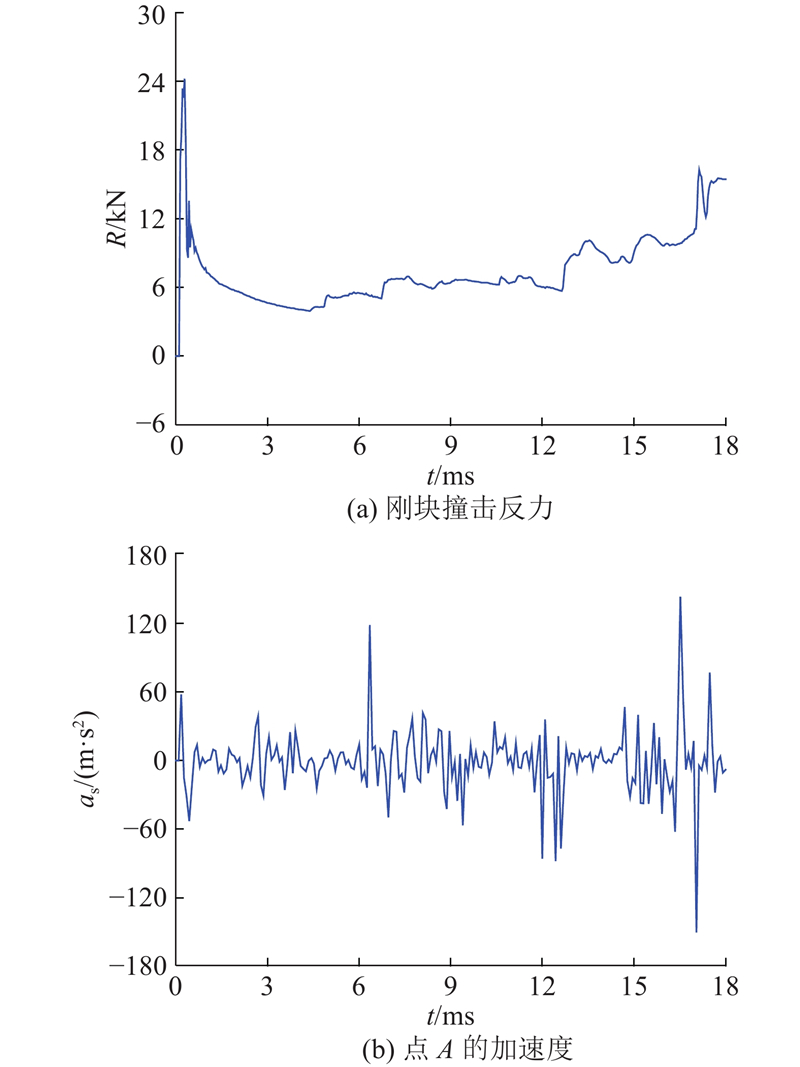
薄壁金属方管具备良好的耗能特性,在结构抗震和汽车防撞吸能盒设计中都有广泛应用. 以如图12所示几何尺寸和材料的薄壁方管为例,将其一端固定,另一端用一大质量刚体块沿轴向撞击,刚块质量m0=800 kg,撞击速度v0=9.5 m/s. 由于惯性,撞击会导致管壁产生连续动力屈曲,并伴随波浪式卷曲折叠的传播与扩展. 该过程包括了材料大变形、动力屈曲、碰撞接触等多种强非线性行为,也是检验动力学算法可靠性的典型算例[28-29]. 为减少计算量,只取方管的1/4对称部分分析,各侧面布置129×31个离散质点,模拟时长共18 ms. 对于管壁皱曲过程中的自接触现象,采用显式拉格朗日乘子法[4]求出接触力并反向施加到相应范围的质点上. 管体材料的应力-应变关系符合Johnson-Cook模型,计入撞击后的应力硬化和应变率效应影响,满足混合强化法则并取参数β=0.5.
图 12
图 12 薄壁方管受刚块撞击:几何尺寸、材料与约束条件
Fig.12 Geometry, material and constraints of thin-wall rectangular tube subjected to rigid-body impact
采用以上模型计算得到刚块撞击反力R随时间变化情况及管端部一点A处的纵向加速度az时程曲线分别如图13(a)和(b)所示,图中的一系列峰值点对应着管体受撞击后发生的连续多次屈曲现象. 图14给出了撞击后动力屈曲演化过程中t=3.5、9.6、12.8、17.4 ms方管的变形情况. 可以看到,管端被撞击后承受的冲击力迅速增大,使其靠近刚块一端进入塑性状态,并导致约t=3.5 ms第1层波状皱曲出现并形成塑性铰;之后,由于管壁皱曲,能量被吸收,同时方管刚度减小,刚块撞击反力也有所降低;但随着皱曲扩展,撞击应力波回弹,同时波浪式翻卷的管壁之间发生挤压,接触力逐渐增大,皱曲部位继续产生塑性应变强化,因此刚块反力又呈现出一定的上升趋势;最终,撞击能量通过管壁连续屈曲形式被完全吸收,在各个侧面上形成4层明显的波状皱曲. 图15还给出了第4层皱曲发生后(约t=13.4 ms)管壁内外两侧的等效塑性应变云图,最大值分别为1.348和1.502,表明此时已产生较大塑性变形.
图 13
图 14
图 14 受撞击后不同时刻的方管形态
Fig.14 Deformed shape of box tube at different moments after impacting
图 15
图 15 t=13.4 ms时方管壁表面的等效塑性应变分布
Fig.15 Equivalent plastic strain distribution on tube walls at time of 13.4 ms
算例结果表明,尽管管壁材料已产生极大变形,但本文方法仍然实现了对撞击后全过程的有效模拟. 整个计算中没有额外设置特殊技巧或进行人工参数的修正,也没有出现因强非线性行为而导致的数值不稳定现象,反映出本文方法的良好性能.
5. 结 语
本文将有限质点法应用于求解薄壳结构的动力非线性问题. 构造了具有大转动大变形分析能力的薄壳离散计算模型,建立了质点和壳元的基本控制方程与计算公式,并对质点转动惯量、临界时间步长等关键参数取值问题提出了合理可行的处理策略. 针对薄壳质点位移及壳元变形与内力均按照面内拉压和面外弯扭两部分进行拆分和组合,并着重推导了与面外弯扭刚度相对应的质点内力(矩)计算公式,给出了质点切平面外转角变步长显式时间积分式. 与直接构建高阶的等参曲面壳元相比,这种组合内力分块计算方式简单,运算量小,也避免了因剪切自锁和零能模态等问题而带来的求解困难. 此外,还在质点内力求解模块引入了基于J2塑性理论的平面应力通用本构积分算法,建立了算法的具体实现步骤,可用于分析理想弹塑性、混合应力强化、率相关塑性等多种材料模型. 通过多个典型数值算例对本文方法进行了测试,并将模拟结果与相关文献的数值和试验结果进行了对比,表明该方法从理论到程序均能有效求解考虑薄壳几何与材料大变形的爆破冲击、撞击等动力非线性问题,且具有较高精度.
有限质点法不对结构的线性和非线性运动变形加以区别,也不存在非线性迭代的概念,而采取统一的分析模式. 另外,质点在内力和外力作用下,其运动状态是永恒的,质点控制方程的解本身就是结构的动力响应,其动力分析过程更加真实结构的行为过程. 这些特点使得非线性和动力分析在有限质点法中成为一种自然的过程. 因而该方法在薄壳结构动荷载下的强非线性行为计算中有很大的优势和灵活性,给薄壳研究中的这类问题求解提供了新的思路和强有力的解决方法.
参考文献
A Study of three-node triangular bending elements
[J].
Advances in one-point quadrature shell elements
[J].DOI:10.1016/0045-7825(92)90100-X [本文引用: 1]
Non-linear explicit dynamic analysis of shells using the BST rotation-free triangle
[J].DOI:10.1108/02644400210439119 [本文引用: 1]
Dynamic analysis of membrane systems undergoing overall motions, large deformations and wrinkles via thin shell elements of ANCF
[J].
An isogeometric solid-like shell element for nonlinear analysis
[J].DOI:10.1002/nme.v95.3 [本文引用: 1]
A continuum mechanics based four-node shell element for general non-linear analysis
[J].DOI:10.1108/eb023562 [本文引用: 1]
Nonlinear finite element analysis of shells: Part I. three-dimensional shells
[J].DOI:10.1016/0045-7825(81)90121-3 [本文引用: 1]
Higher-order MITC general shell elements
[J].
结构复杂行为分析的有限质点法研究综述
[J].
Review of the finite particle method for complex behaviors of structures
[J].
基于有限质点法的多尺度精细化分析
[J].
Multi-scale fine analysis based on the finite particle method
[J].
考虑Cowper-Symonds黏塑性材料本构的向量式有限元三角形薄壳单元研究
[J].
Study on triangular thin-shell element of vector form intrinsic finite element considering Cowper-Symonds viscoplastic constitutive model
[J].
薄壳结构碰撞、断裂和穿透行为的向量式有限元分析
[J].
Collision-contact, crack-fracture and penetration behavior analysis of thin-shell structures based on vector form intrinsic finite element
[J].
An efficient numerical shape analysis for light weight membrane structures
[J].DOI:10.1631/jzus.A1300245 [本文引用: 3]
Problems encountered from the use (or misuse) of Rayleigh damping
[J].DOI:10.1002/(ISSN)1096-9845 [本文引用: 1]
Finite element formulations for large deformation dynamic analysis
[J].DOI:10.1002/(ISSN)1097-0207 [本文引用: 4]
Advances in the formulation of the rotation-free basic shell triangle
[J].DOI:10.1016/j.cma.2004.07.039 [本文引用: 4]
Nonlinear dynamic analysis of shells with the triangular element TRIC
[J].
Experimental and theoretical studies of explosive-induced large dynamic and permanent deformations of simple structures
[J].DOI:10.1007/BF02326708 [本文引用: 2]
A simple triangular curved shell element
[J].DOI:10.1108/eb023574 [本文引用: 1]
Crashworthiness of aluminum/CFRP square hollow section beam under axial impact loading for crash box application
[J].