离心泵在石油化工、电力、纸浆造纸、通用工业、工业锅炉给水和核电系统辅助供水方面得到广泛应用,约占各类泵总量的70%,年均耗电量超过总发电量的10%. 对离心泵进行效率优化不仅对提高离心泵性能具有重大意义,也能产生巨大的社会效益和经济效益. 目前已有大量基于水力损失模型的离心泵结构优化,如杨军虎等[1]基于水利损失模型优化叶片出口安放角、叶片数从而提高离心泵的效率. 高江永[2]利用水力损失模型进行多变量优化设计,对优化后的离心泵进行损失预测并研究多变量对效率的影响大小和排序. 聂松辉等[3]将水力损失模型作为优化计算模型并以无驼峰、无过载的理论不等式作为约束条件对离心泵进行水力效率优化. 在以上文献中,水力损失模型及优化约束条件公式都是在设计工况点下的半经验半理论推导公式,优化方法简单快速,设计周期短,但是无法研究离心泵在其他工况点的水力效率,公式中系数的选择与修正均依据大量优秀水泵模型,与离心泵过流部件的几何形状密切相关.
此外,目前已有大量国内外学者利用近似模型来优化各类水泵性能,如王春林等[4]建立二次响应面(quadratic response surface function,RSF)近似模型对旋流泵效率、高效区宽度和无驼峰性能进行优化设计,王文杰等[5]利用克里金响应面(Kriging response surface function,KRG)近似模型在2个工况点优化离心泵的叶片进口冲角、包角及出口安放角3个参数以提高效率. Bellary等[6-7]提出利用近似模型分别对工业离心泵和电子潜水泵的叶片进出口安放角进行效率优化设计. Heo等[8]以离心泵的叶片数、叶片进出口安放角和叶轮后盖板轮廓形状为设计变量,对比使用3种近似模型进行效率优化. 谈明高等[9]针对数值模拟法和水力损失法对离心泵性能预测的精度进行数值量化比较. 王丹[10]以蜗壳内水力损失和叶轮摩擦损失之和的极小值作为目标函数进行结构优化. 马艺等[11]在传统的离心泵无过载设计公式的基础上,提出据速度系数法,可以较准确地推导中比转速多级离心泵无过载叶轮设计公式. 张宇等[12]基于拉丁超立方抽样、计算流体动力学(computational fluid dynamics,CFD)数值模拟和克里金响应面插值等方法,以离心泵性能参数中的效率和必须汽蚀余量为优化目标,采用二代非劣排序遗传算法(non-dominated sorting genetic algorithm II, NSGA-II)在设计域上求解离心泵性能多目标优化问题. 目前随着CFD分析技术的高速发展和近似模型代理函数响应能力的提高,有必要对水力损失法和近似模型法的计算精度进行量化比较,以指导离心泵优化方法的选择. 综上,对离心泵效率的优化,主要有水力损失法和近似模型法2种优化方法,前者基于半理论半经验公式结合优化算法对离心泵进行优化设计,后者将CFD分析技术与近似模型相结合进行离心泵优化设计. 2种方法的研究均独立进行,未进行过计算精度和有效性的比较.
以中开多级(multistage dual,MSD)离心泵优化设计为例,基于水力损失模型进行设计变量灵敏度分析,选择出关键设计变量;分别利用水力损失、完全二次响应面、径向基高斯响应面(radial basis Gaussian response surface function,RBF)和克里金响应面4种近似模型优化该离心泵的关键设计变量;通过遗传算法确定单级离心泵设计工况点下的关键设计变量Pareto最优解,得到工作性能较好的叶轮.
1. MSD离心泵设计变量分类
1.1. 优化设计方案
MSD中开多级(10级)离心泵的设计要求如下:体积流量qV=100 m3/h,扬程H=80 m(每级),转速n=2 950 r/min,配套电机的额定输出功率Pr=355 kW,通过计算得到比转速
图 1
离心泵的设计变量较多,主要有叶片数Z、叶轮进口直径
1.2. 离心泵变量范围
表 1 多级泵设计变量取值范围
Tab.1
| 设计变量 | 范围 |
| Z | [3, 7] |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
1.3. 设计变量的灵敏度分析
式中:
蜗壳的水力损失包括流道摩擦损失
式中:
水力损失为
水力损失模型中的扬程表达式为
式中:Ht为理论扬程.
水力效率
式中:
图 2
图 2 单变量对单级离心泵外特性值的影响曲线
Fig.2 Effect curve of univariate on external characteristic values of singlestage centrifugal pump
灵敏度
式中:f1为某设计变量在单调区间内增加2%后单级离心泵的效率或扬程,f0为各设计变量均为默认值时单级离心泵的效率或扬程.
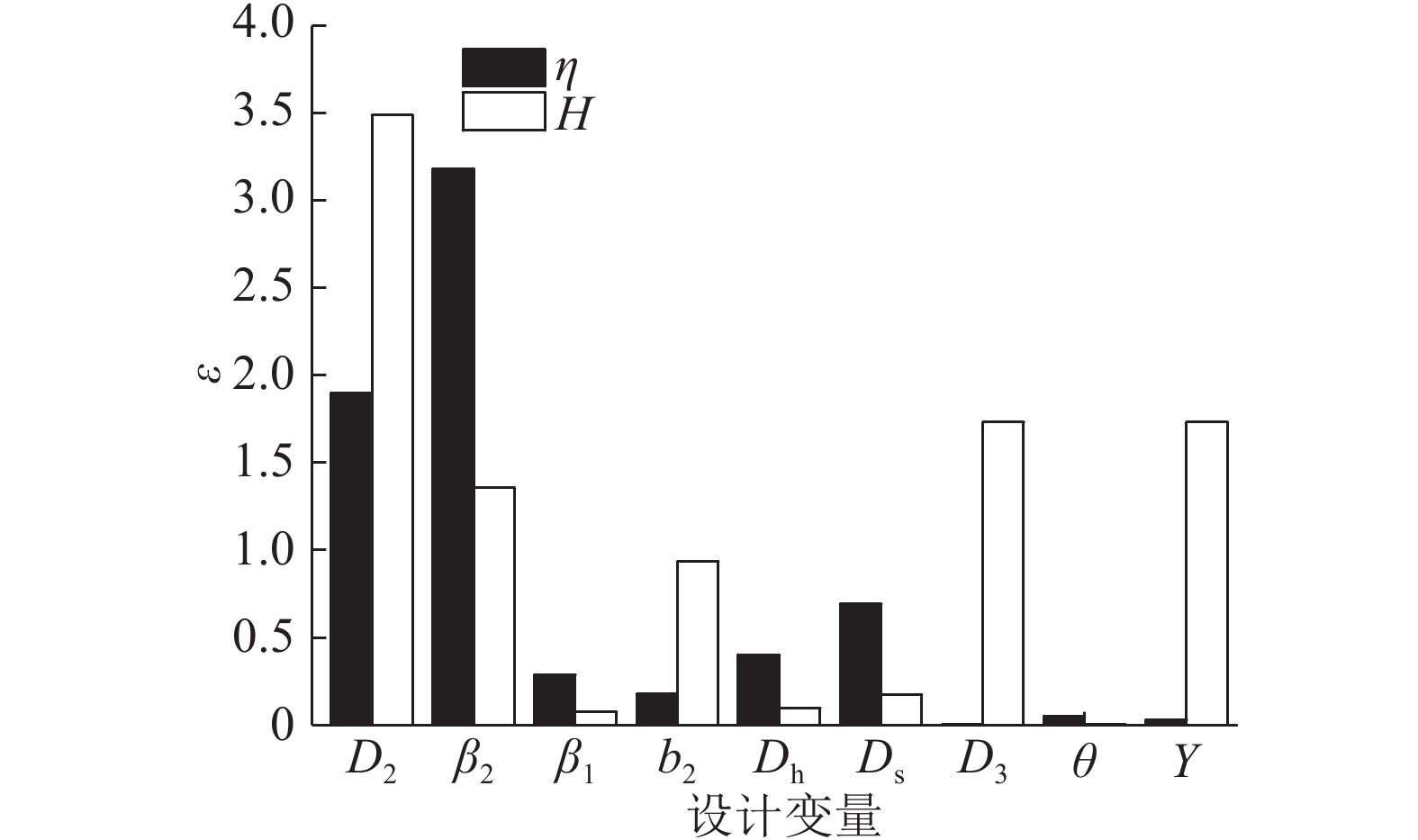
由图3可知,
图 3
图 3 离心泵设计变量灵敏度分析
Fig.3 Sensitivity analysis for design variables of centrifugal pump
2. MSD离心泵近似模型建立
2.1. 离心泵CFD数值仿真试验
若选择的离心泵设计变量较多,则近似模型的建立需要大量样本数,消耗较大的计算时间与人力物力. 若合理选择关键设计变量,在合理充分的样本数下,运用近似模型可以对离心泵性能进行多目标优化,如最高效率、高效区宽度、抗汽蚀性能等. 对于
MSD中开单级离心泵数值模拟的计算域分为吸水室、叶轮、蜗壳和扩散管. 样本离心泵利用CFturbo、ICEM、Fluent进行CFD数值仿真,网格模型如图4所示. 湍流模型选择雷诺时均中的RNGk-ε模型,并设置速度入口和自由出流边界条件. 首先进行网格无关性验证,比较计算误差和计算时间的长短. 全局网格最大尺寸设为8 mm、最小网格尺寸设为0.5 mm、叶片的最大网格尺寸设为2 mm、内部交界面最大网格尺寸设为4 mm,调节网格质量保证网格质量达到0.4以上. 根据0.2qV、0.4qV、0.6qV、0.8qV、1.0qV、1.2qV、1.4qV、1.6qV、1.8qV、2.0qV、2.2qV、2.4qV共12个工况点的CFD数值仿真,计算分析得到各样本离心泵在对应工况点的扬程、轴功率和水力效率,并依此拟合MSD中开单级离心泵外特性曲线,从而计算
图 4
2.2. 基于3种近似模型的响应
应用RSF、RBF研究设计变量
响应面模型有效性检验标准采用均方根误差和决定系数:
式中:
根据设计变量可知,二次响应面模型分为含有10个未知参数的完全二次响应面模型和7个未知参数的不完全二次响应面模型. 响应函数分别为
式中:xi、xj(i, j=1, 2, 3)为样本点中关键设计变量;A1、A2为关键设计变量组成矩阵;C1、C2为二次响应面函数的系数矩阵.
径向基高斯响应面近似模型结构简单,训练简便,可以拟合任意非线性函数,所需样本数较少. 结构一般分为输入层、隐藏层和输出层,隐藏层神经元变换函数即径向基核函数表达式为
式中:r为欧氏距离;σ为自由参数;X、Xi为2个样本.
从训练集样本点中随机抽取n组设计变量作为高斯函数的中心,则径向基高斯响应面的输出表达式为
式中:
式中:
通过RBF得到的优化模型为
式中:D为关键设计变量x的1×n维高斯距离矩阵,
克里金响应面模型具有全局特性,用于在已知60组离心泵外特性值的基础上预测离心泵性能. 表达式由回归模型和高斯相关模型两部分组成:
式中:
式中:
式中:
2种二次响应面计算模型和径向基高斯响应面计算模型的均方根误差和决定系数如表2所示. 比较完全RSF与不完全RSF模型的均方根误差和决定系数,完全RSF模型拟合准确度较高,所以在后续计算模型中选择完全RSF模型进行运算,简称RSF. RSF、RBF的均方根误差接近0,决定系数接近1.0,说明2种近似模型的拟合准确度均较高.
表 2 响应面模型有效性检验
Tab.2
| 近似模型 | RMSE/% | R2/% | |||||
| H | P | η | H | P | η | ||
| 不完全RSF | 0.10 | 0.24 | 0.26 | 96.96 | 94.41 | 82.34 | |
| 完全RSF | 0.08 | 0.15 | 0.21 | 97.81 | 97.78 | 89.33 | |
| RBF | 0.10 | 0.22 | 0.25 | 97.19 | 95.46 | 84.20 | |
2.3. 3种近似模型精度验证
比较与验证构建的3种近似模型的预测精度,同样采用拉丁超立方取样方法在设计空间中建立3种不同近似模型的测试样本集,即对关键设计变量另抽取样本数目为20的测试集,并利用本研究采用的数值模拟方法求出测试点相应的离心泵外特性值. 将测试点设计变量代入完全二次响应面模型、径向基高斯响应面模型和克里金响应面模型中,得出离心泵外特性预测值,并与CFD数值模拟计算值进行对比.
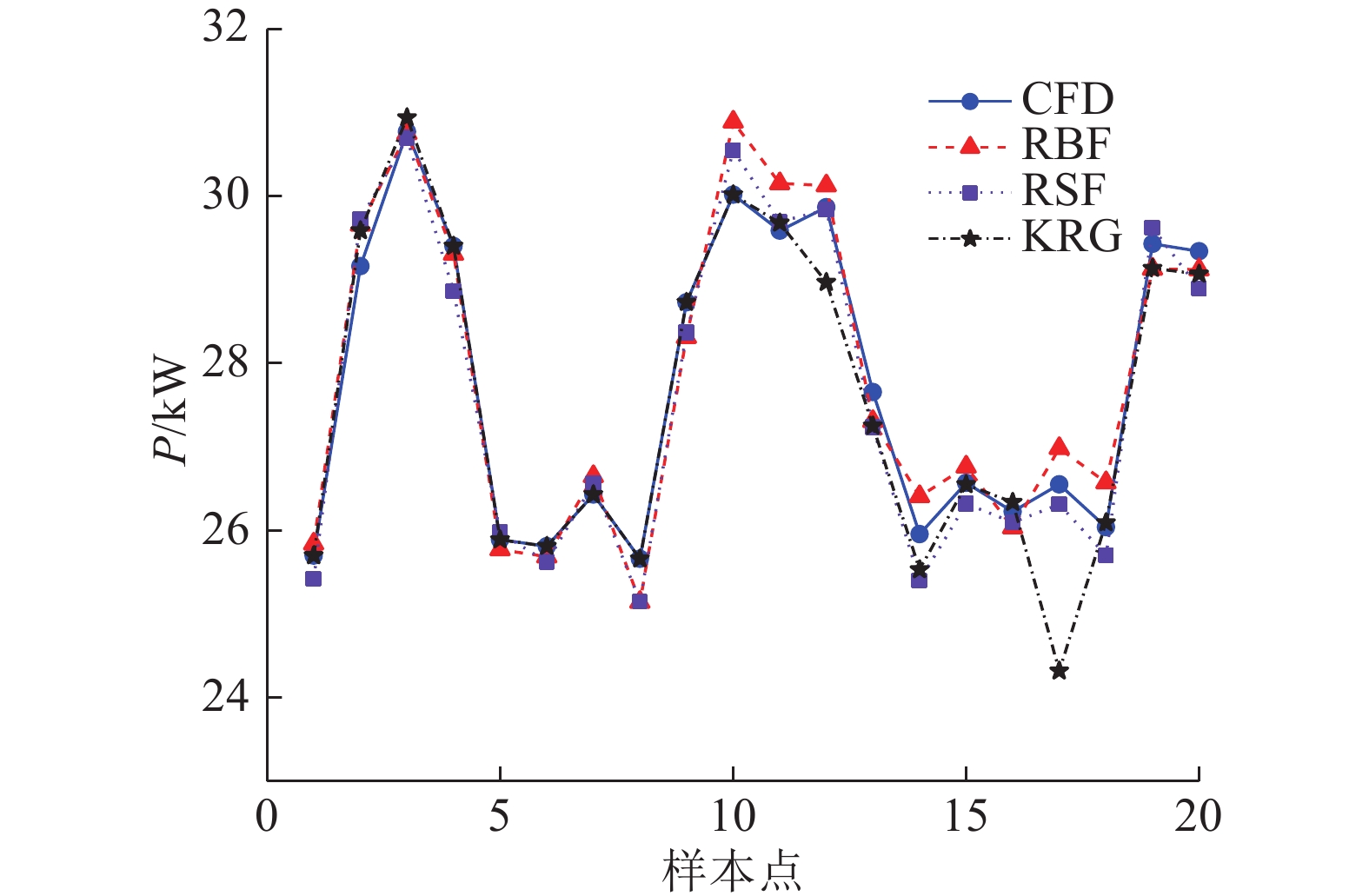
图 6
图 6 近似模型水力功率预测值与CFD数值计算结果对比
Fig.6 Comparison of approximate model predicted hydraulic power with CFD numerical calculation result
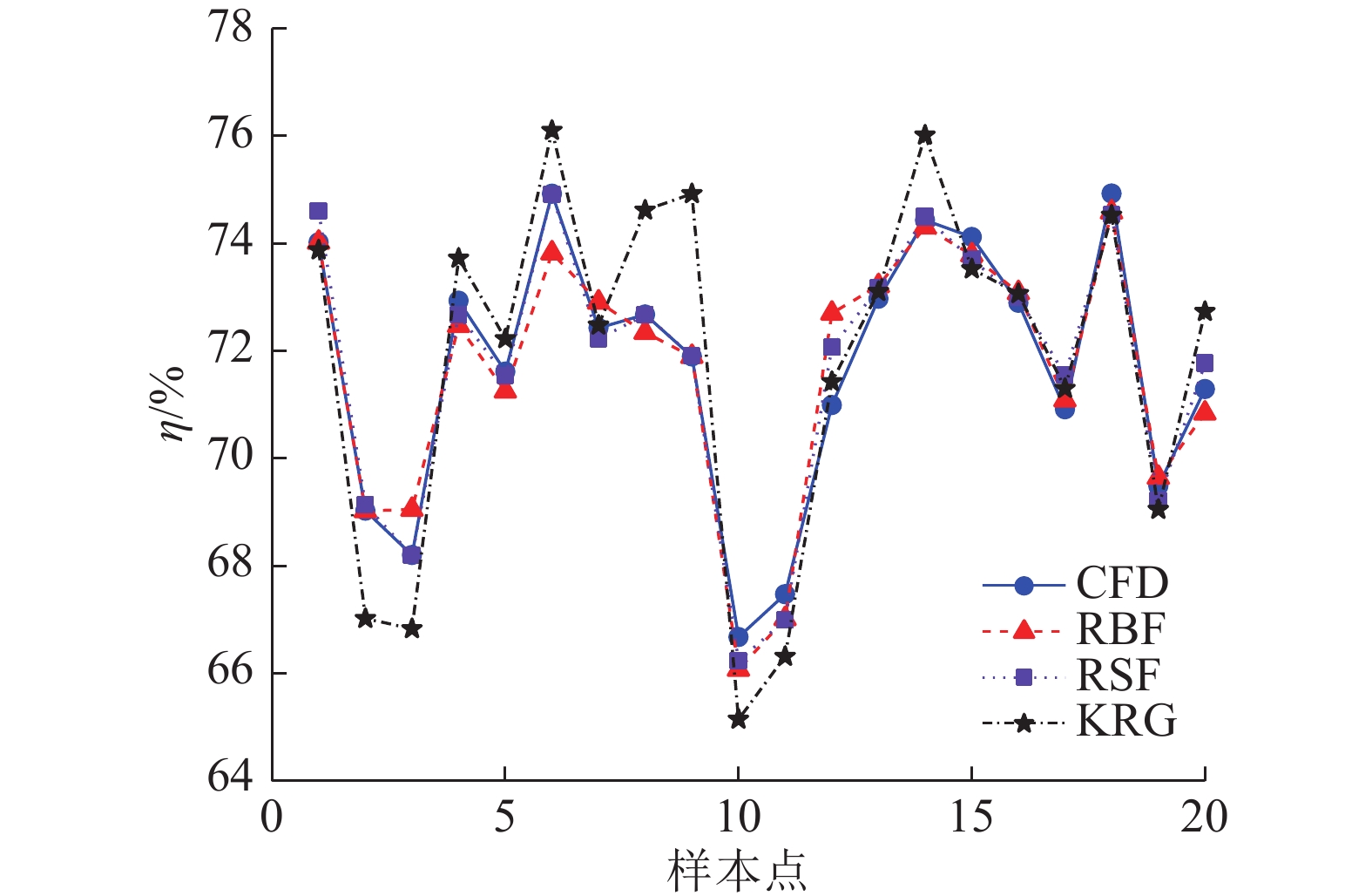
图 7
图 7 近似模型效率预测值与CFD数值计算结果对比
Fig.7 Comparison of approximate model predicted hydraulic power with CFD numerical calculation result
总的来说,3种近似模型对效率的预测精度低于其对扬程和水力功率的预测精度,主要原因是20组样本测试集的水力效率由公式计算得出,其计算结果误差由扬程和水力功率数值计算误差累积而成. 综合比较3种不同近似模型得出的离心泵外特性预测值与CFD数值模拟值,完全二次响应面模型预测精度最高,径向基高斯响应面模型预测精度次之,克里金响应面模型预测精度最低.
3. 模拟寻优结果分析
3.1. 二代非劣排序遗传算法
不同于单目标优化,多目标优化存在不唯一解,即存在被称为Pareto最优解集的最优解集合,其中元素被称为Pareto最优解或非支配解. Pareto最优解的定义如下:对于可行解
集合
3.2. 基于二代非劣排序遗传算法寻优
水力损失模型和二次响应面、径向基高斯响应面及克里金响应面近似模型3种不同近似模型的优化目标函数和变量分别为
式中:Hmax、ηmax分别为扬程和效率最大值.
针对单级离心泵的扬程,根据国家标准GB/T5657-2013《离心泵技术条件(Ⅲ类)》[17],离心泵扬程的规定容差系数为3%,所以定义单级离心泵的设计扬程
在本研究中,
3种不同近似模型的总效率为
式中:
针对以上水力损失(hydraulic loss, HLoss)模型和3种近似模型优化方案,通过遗传算法分别得到单级离心泵设计工况点下关键设计变量最优解,并经CFD仿真分析计算,结果如表3所示.
表 3 4种计算模型Pareto最优解及CFD数值模拟分析
Tab.3
| 模型 | D2/mm | b2/mm | β2/(°) | 模型理论计算值 | CFD仿真计算值 | 误差/% | ||||||||
| H/m | P/kW | η/% | H/m | P/kW | η/% | H | P | η | ||||||
| HLoss | 273.9 | 14.0 | 17.0 | 82.40 | 26.51 | 75.98 | 76.89 | 24.55 | 74.10 | 7.15 | 7.98 | 3.78 | ||
| RSF | 279.0 | 13.0 | 15.0 | 84.19 | 26.11 | 77.32 | 83.77 | 26.03 | 77.26 | 0.50 | 0.31 | 0.08 | ||
| RBF | 277.0 | 14.5 | 15.0 | 83.13 | 26.30 | 75.85 | 83.09 | 26.00 | 76.63 | 0.50 | 1.15 | 1.02 | ||
| KRG | 275.0 | 15.5 | 15.0 | 84.06 | 26.69 | 75.02 | 82.13 | 25.98 | 75.81 | 2.35 | 2.73 | 1.04 | ||
3.3. 结果及分析
根据表3中4种优化计算模型最优关键设计变量、理论计算外特性值、相应的CFD数值模拟分析计算值和误差大小的对比分析,水力损失计算模型对于离心泵外特性值的计算准确度较低,利用理论公式计算得出的扬程、功率与CFD计算得出的扬程、功率相差较大,且CFD计算扬程不满足设计要求. 造成这样结果的原因为,水力损失模型是半经验半理论推导公式,其中系数的选取对计算结果有较大影响,同时修正系数又是根据统计规律给出的,须合理选择与考虑,且与过流部件的几何形状密切相关. 另外,在离心泵内部流场中容易产生旋涡流动,由旋涡流动造成的扬程和效率损失难以用理论公式推导进行准确计算. 因而,水力损失法较近似模型法虽具有一定的实用性,但是适用性往往较差. 在近似模型法中,CFD数值模拟分析得出的计算结果精度较高,其自身响应函数映射能力较强,因此与水力损失法相比,结果更加准确.
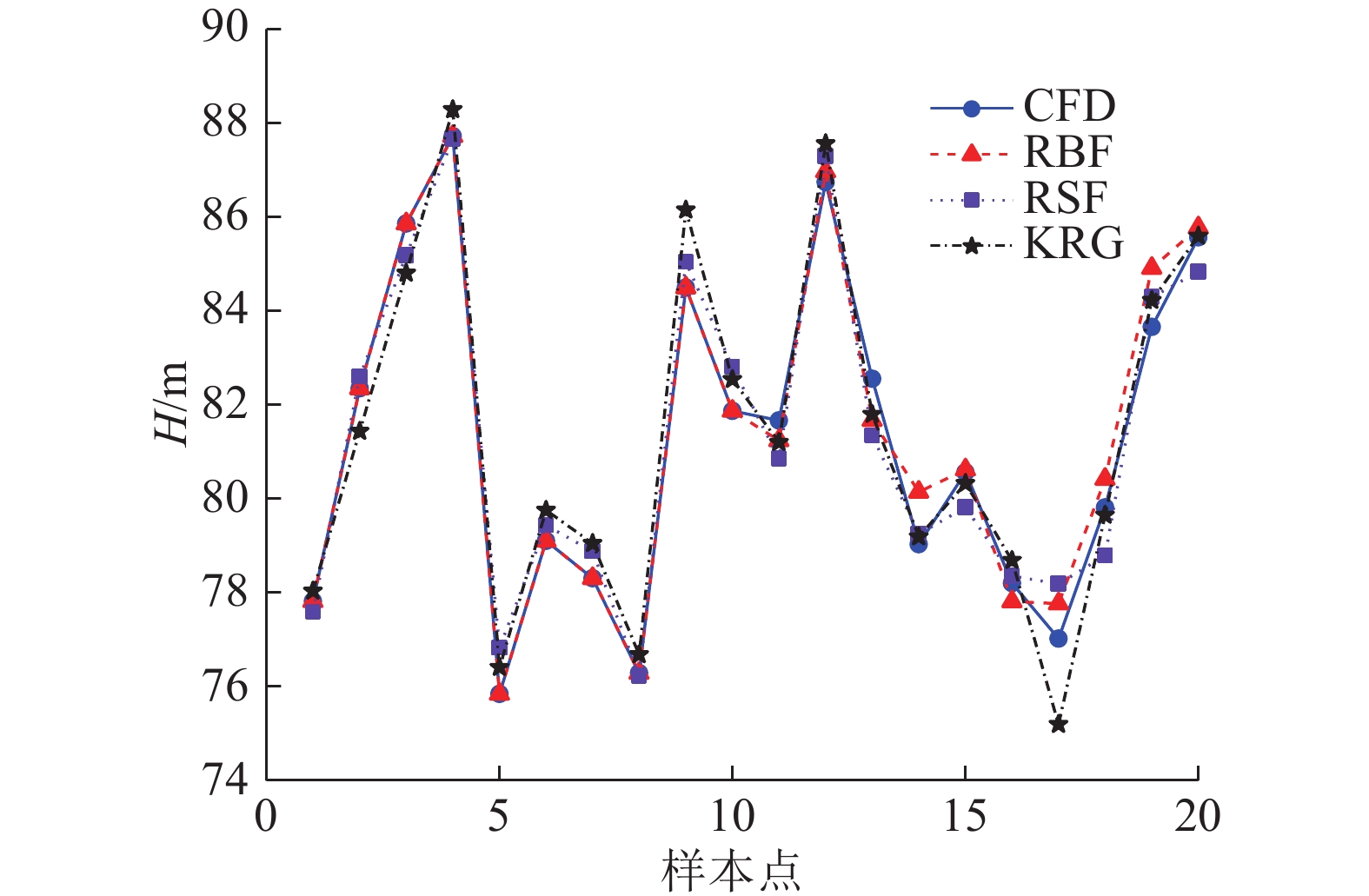
图 5
图 5 近似模型扬程预测值与CFD数值计算结果对比
Fig.5 Comparison of approximate model predicted head value with CFD numerical calculation result
图 8
图 8 叶轮1、2的单级离心泵全流量性能预测
Fig.8 Full flow performance prediction of singlestage centrifugal pump with impeller 1 and 2
通过RSF、RBF近似模型得到单级离心泵叶轮的设计结构参数并建立三维模型. 为了全面准确地预测单级离心泵在非设计工况即小流量和大流量工况下的工作性能,对单级离心泵内流场进行多工况CFD数值模拟分析,进而对拟合出的外特性曲线进行性能预测,结果如图8所示.
作
可见经优化后的叶轮高效区相对宽度较大.
针对MSD中开多级离心泵中所有叶轮的效率优化方法与本研究中单级离心泵效率优化方法是一致的. 基于叶轮1、2的首级叶轮优化效果,采用同样的方法进行次级叶轮优化,所有次级叶轮的结构参数一致,从而可以预测全流量下10级中开多级离心泵的整泵性能.
4. 结 论
基于水力损失模型进行单级离心泵设计变量灵敏度分析,分析结果与前人关于泵设计参数对性能影响的研究结果相符,凭此筛选出关键设计变量. 根据水力损失法和近似模型法并结合NSGA-Π遗传算法对单级离心泵的关键设计变量进行多目标优化,比较基于各模型的单级离心泵的内流场分析结果,选择确定基于RSF、RBF的叶轮1、2. 在设计流量下,叶轮1的扬程为83.77 m,效率为77.26%;叶轮2的扬程为83.09 m,效率为76.63%. 结合基于近似模型的离心泵效率优化方法和遗传算法可以提高离心泵的水力效率和高效区宽度. 利用该方法不仅可以准确预测扬程、功率、效率及高效区宽度,还可以预测速度场、压力场、漩涡等内部分布,即可以同时预测离心泵的内特性和外特性. 在小流量工况下,基于叶轮1的整台泵高效区范围大于基于叶轮2的整台泵高效区范围;在大流量工况下,基于叶轮1的整台泵高效区范围小于基于叶轮2的整台泵高效区范围. 所以对基于叶轮1的整台泵或者基于叶轮2的整台泵的开模制造须根据企业实际工作需求进行选择确定.
参考文献
基于水力损失计算的离心泵叶轮叶片出口安放角选择方法
[J].
Method for selecting centrifugal pump impeller outlet angle based on calculation of centrifugal pump impeller's hydraulic loss
[J].
基于遗传算法的离心泵优化设计
[J].
Optimization design of centrifugal pump based on genetic algorithm
[J].
基于响应面法的旋流泵优化设计
[J].
Optimization for vortex pump based on response surface method
[J].
基于Kriging模型和遗传算法的泵叶轮两工况水力优化设计
[J].
Two-point hydraulic optimization of pump impeller based on kriging model and neighborhood cultivation genetic algorithm
[J].
Effectiveness of meta-models for multi-objective optimization of centrifugal impeller
[J].
Application of computational fluid dynamics and surrogate-coupled evolutionary computing to enhance centrifugal-pump performance
[J].
High-efficiency design optimization of a centrifugal pump
[J].
离心泵水力损失的计算
[J].
Calculation of hydraulic loss in centrifugal pumps
[J].
中比转速无过载多级离心泵的叶轮设计方法
[J].
A novel design method for impeller of medium specific speed non-overload multistage centrifugal pump
[J].
基于克里金响应面元模型的离心泵水力性能多目标优化
[J].
Kriging based muti-objective optimization for hydraulic performance of centrifugal pump
[J].
Analysis of effect of impeller geometry including blade outlet angle on the performance of multi-pressure pumps: Simulation and experiment
[J].
Numerical investigation of the effect of number of blades on centrifugal pump performance
[J].