目前最常用的MRI磁体冷却方法是低温液体浸泡法,通过在磁体外围安装贮液槽,先后充注液氮和液氦将磁体冷却至液氦温区[4-6]. 该方法看似操作方便、结构简单,但因为磁体热容过大,每次冷却需数千升液氮和液氦[2],资源损耗较大,成本高昂. 为了减少低温液体用量,Hoenig[7]最早提出使用制冷机直接冷却磁体的方法,此后Watanabe等[8-11]、Iwasa等[12]、Giebeler等[13]、Jin等[14-17]、Anashkin等[18-19]、Dai等[20-22]均分别使用脉管制冷机等成功将磁体冷却至液氦温区. 但是由于制冷机在该温区冷量极低,此方法须磁体与制冷机距离较近,并通过金属带等机构以导热方式传递冷量从而减少冷量耗散,从而引入了引线焦耳热、运行振动以及电磁干扰等不利因素;此外冷量过小会导致磁体温度均匀性差、降温速率慢等问题. 因此,对于重达数吨的MRI磁体而言难以适用,目前多用于冷却小型低温超导磁体.
针对现有冷却方法的缺陷,基于自主研发的大冷量斯特林制冷机,提出MRI低温超导磁体冷却系统,可将磁体快速均匀冷却至60 K以下,之后再用少量液氦将其冷却至超导温度. 此方法可在保证磁体降温速率的前提下,完全取代传统冷却方法中的液氮浸泡过程并减少约50%的液氦用量,同时可消除制冷机对磁体的诸多不利影响. 通过建立数学物理模型并利用Matlab开展数值模拟,对系统进行参数分析和优化设计,预测冷却时间等性能参数.
1. 系统设计
如图1所示为基于大冷量斯特林制冷机的MRI低温超导磁体冷却系统流程示意图,主要部件包括待冷却MRI磁体、斯特林制冷机、低温风机、氦气瓶以及低温调控阀等. 图中,P、T分别代表压力、温度传感器. 系统主体采用真空绝热管串联各部件为环路,管内充注氦气,制冷机与MRI设备柔性连接且距离较远,可避免振动和电磁干扰等影响. 氦气作为冷量传递介质,从制冷机冷端换热器带走冷量并由低温风机驱动至磁体周围的环形流道内将磁体均匀冷却. 系统可根据功能分为以下4个单元. 1)制冷机单元,主要包括实验室自主研发的大冷量单级斯特林制冷机. 结构为曲柄连杆驱动的整体式同轴型,在液氮温区可提供超过1 kW冷量(输入电功率为11 kW),最低制冷温度低于40 K,具有冷量大、制冷效率高、制冷温区广、降温速率快、启动迅速、结构紧凑等优点[23-26]. 冷端换热器为管束式结构,如图2所示,在进出口处布置压力和温度传感器以实时监测氦气进出制冷机的状态参数. 2)动力控制单元,主要包括低温风机、低温调控阀、低温截止阀等,可提供氦气循环动力并实现质量流量控制,此单元须置于冷箱中以减小外界漏热. 3)补气单元,主要包括氦气瓶、补气电磁阀等,在冷却过程中可根据设定值向管路补气以保持氦气压力在一定范围内. 4)MRI单元,主要包括待冷却MRI磁体,磁体外流道接口可与管路对接,在出口处布置温度传感器以实时监测温度.
图 1
图 1 MRI低温超导磁体冷却系统示意图
Fig.1 Schematic diagram of cooling system for MRI low temperature superconducting magnet
图 2
2. 数学物理模型及数值计算
2.1. 假设条件
为了简化计算,进行以下假设:1)系统初始温度为室温300 K;2)冷却过程划分为长度小于10 min的时间微元,微元内的物理过程视为稳态;3)管路压降只考虑氦气的沿程阻力损失;4)根据真空绝热管漏热实验的测量结果,假设单位长度管路漏热率为1 W/m;5)氦气流经阀门的热力过程视为等焓过程;6)低温风机等设备绝热良好,忽略漏热;7)磁体外氦气流道横截面为工字型,将其划分为多块矩形截面流道处理.
2.2. 数学物理模型
基于上述假设条件,根据能量守恒以及连续性方程等建立系统各部件的数学物理模型.
2.2.1. 制冷机冷端换热器
能量守恒方程为
式中:qm_cin、qm_cout分别为制冷机冷端换热器进、出口氦气的质量流量,Kc为冷端换热器与氦气之间的传热系数,Ac为冷端换热器的总换热面积,ΔT1为氦气与冷端换热器壁面之间的对数传热温差,hcin、hcout分别为冷端换热器进、出口氦气的比焓,Qc为当前制冷温度下斯特林制冷机可输出的冷量.
冷端换热器的对流传热系数可由式(2)、(3)所示的Gnielinski传热关联式[27]求解,换热管壁厚为0.5 mm,忽略径向导热温差.
式中:Nu为努塞尔数,Re为流体雷诺数,Pr为流体普朗特数,d、l分别为流道当量直径和长度,Tf、Tw分别为流体、流道壁面温度,f为Darcy阻力系数.
斯特林制冷机的制冷量可近似视作制冷温度Tc的单值函数. 经实验测量和函数拟合,本台单级斯特林制冷机的制冷量与制冷温度之间存在如下函数关系:
2.2.2. 磁体
能量守恒方程为
式中:qm_Min、qm_Mout分别为磁体进、出口氦气的质量流量,KM为磁体与氦气之间的传热系数,AM为磁体的总换热面积,ΔT2为氦气与磁体的对数传热温差,hMin、hMout分别为磁体进、出口氦气的比焓,mM为磁体的总质量,cM为磁体的比热容,ΔTM为单位时间内磁体的温度变化量.
MRI设备的流道横截面积较大,氦气在其内部流速较低,处于层流充分发展状态,故对流传热系数可根据流道特征尺寸查表取值(矩形流道特征尺寸为长宽比)[28]. 为了便于计算不同长宽比结构的传热系数,根据表中数据可将努塞尔数拟合为关于长宽比R的多项式函数:
2.2.3. 低温风机
能量守恒方程为
式中:qm_fin、qm_fout分别为低温风机进出口氦气的质量流量;hfin、hfout分别为低温风机进出口氦气的比焓;Pf为风机输入电功率;ηf为风机的电功转化效率.
2.2.4. 循环管路
能量守恒方程为
式中:qm_tin、qm_tout分别为管段进出口氦气质量流量,htin、htout分别为管段进、出口氦气的比焓,Qt为单位长度管段漏热率,Lt为管段长度.
气体流动压降主要发生在循环管路中,依据以下流阻算式可以计算其数值[29]:
式中:δp为在60 K时氦气在每一循环周期内的压降,ρg为流体密度,g为重力加速度,λ为沿程损失系数,ug为流体平均流速. 其中,λ可根据雷诺数判定流动状态后选用以下算式得出:
式中:δ为管壁粗糙度. 对于光滑无缝钢管可近似取δ=0.01 mm. 当Re<2 300时,流体处于层流状态;当2 300<Re<80d/δ时,流体处于转捩过渡及湍流水力光滑管状态;当80d/δ<Re<4 160(d/(2δ))0.85时,流体处于水力光滑到水力粗糙的过渡状态;当Re>4 160(d/(2δ))0.85时,流体处于湍流水力粗糙管状态.
2.2.5. 低温调控阀
氦气流经调控阀的热力过程近似视为等焓过程:
式中:hvin、hvout分别为阀进出口氦气的比焓.
2.3. 计算逻辑
如图3所示为数值计算逻辑框图. 基于上述数学物理模型,以开启制冷机时系统完全处于室温状态作为初始条件,逐步迭代求解模型中建立的多元非线性方程组,依次解出每个时间微元内系统各部件及氦气的热物性参数. 迭代循环以磁体温度与设定降温目标点之间的大小关系为判据,总迭代次数与时间微元长度之积即为系统冷却时间.
图 3
3. 数值计算结果分析
如表1所示为已知参数条件,包括斯特林制冷机以及MRI等设备的部分几何和性能参数,此外实际安装空间以及设备承压能力等因素也对管路长度、充气压力等有所限制,如充气压力要求小于0.8 MPa.
表 1 Matlab数值计算程序输入参数
Tab.1
| 参数 | 数值 | 单位 |
| 铜基磁体质量 | 500 | kg |
| 铁基磁体质量 | 1 500 | kg |
| 磁体流道横截面积 | 0.3 | m2 |
| 磁体流道换热面积 | 6.1 | m2 |
| 制冷机换热管外径 | 2.5 | mm |
| 制冷机换热管数量 | 90 | − |
| 循环管路总长度 | 11 | m |
| 管路充气压力 | <0.8 | MPa |
3.1. 运行参数优化
冷却时间是系统的关键性能指标,决定冷却效率以及能耗大小. 为了尽可能缩短冷却时间,有必要对运行参数进行优化设计. 结果表明氦气的充气压力和流速对传热效率和压降损失影响显著,存在最优值使冷却时间最短.
3.1.1. 充气压力
图 4
图 5
图 5 充气压力对传热系数和压降的影响
Fig.5 Effect of charge pressure on heat transfer coefficient and pressure drop
3.1.2. 流速
图 6
氦气流速的影响作用同样是源于传热效率与压降2个方面,如图7所示为在充气压力恒定时流速对两者的影响效果. 一方面,氦气流速对制冷机冷端换热器以及MRI的对流传热系数有明显影响,当流速增加时(尤其当流动状态由层流转换为湍流时),对流传热系数明显增大,有效加快系统的冷却过程;另一方面,氦气流速对系统压降影响显著,在流速增加的同时压降会快速上升,对磁体冷却不利. 当充气压力增加时,曲线斜率升高,对冷却时间的影响作用增强.
图 7
图 7 流速对传热系数和压降的影响
Fig.7 Effect of flow rate on heat transfer coefficient and pressure drop
3.2. 系统参数分析
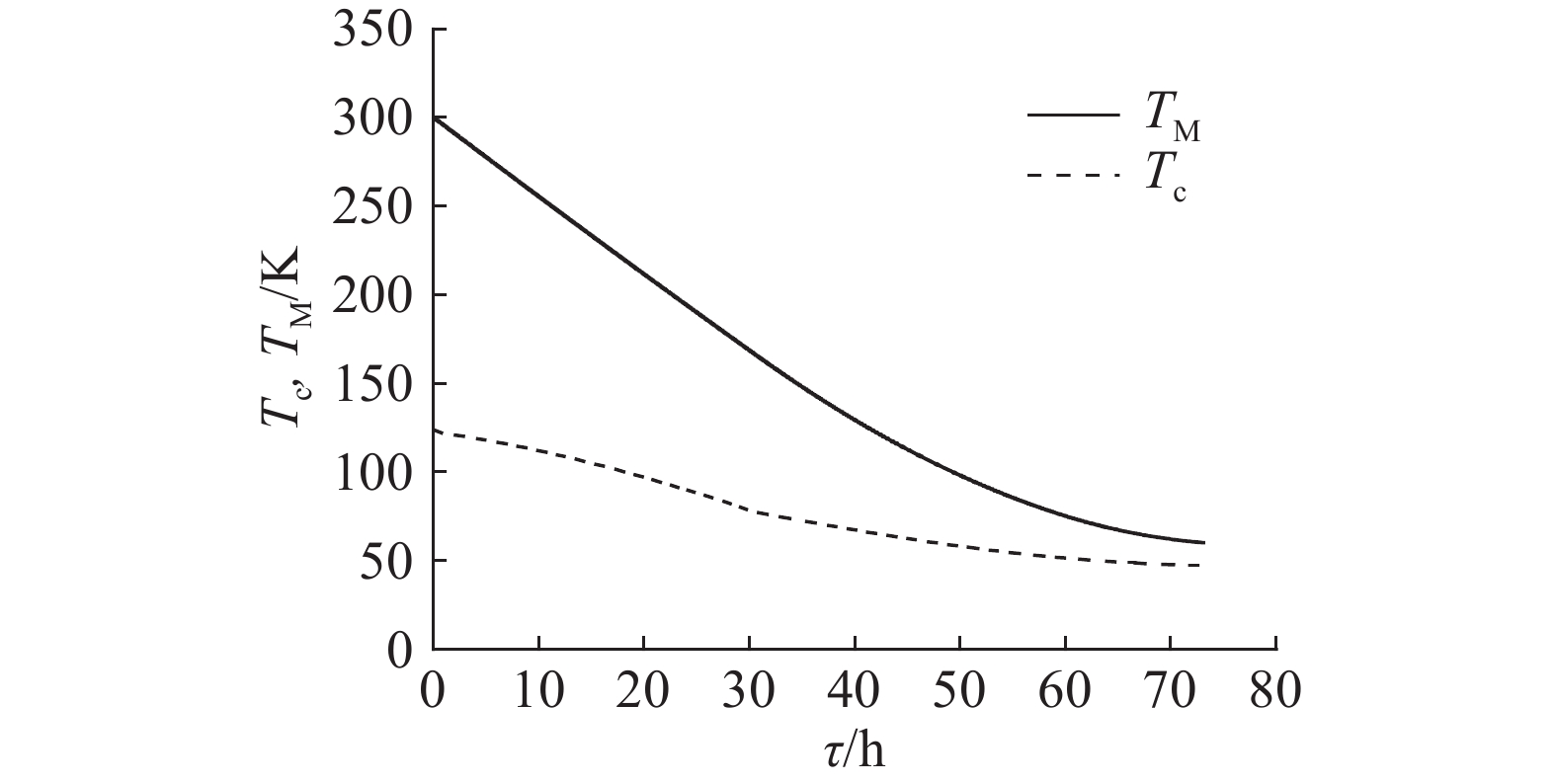
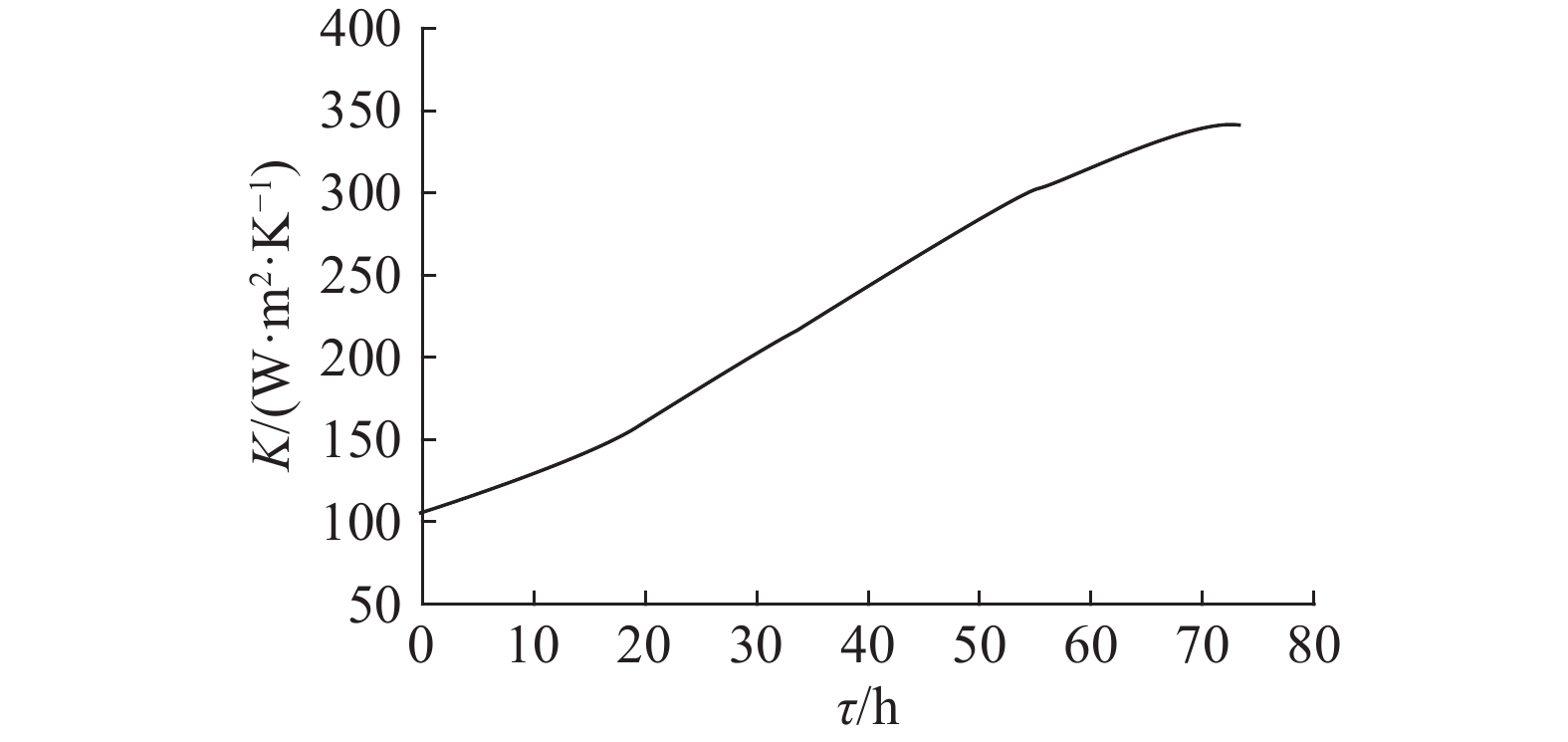
根据参数优化结果,以p=0.300 MPa、u=13 m/s为例分析冷却过程中的参数变化. 在此条件下,系统具有较高的磁体冷却效率,由室温冷却至目标温度60 K仅需73.08 h. 如图8所示为制冷机冷端温度和磁体温度的降温曲线. 图中,Tc为制冷机冷端温度,TM为MRI磁体温度. 由图可知:1)制冷机随冷端温度降低自身输出的冷量相应减少,磁体的降温速率逐渐放缓;2)在冷却初始阶段,磁体温度尚接近室温,而制冷机冷端温度已很快降至约120 K,温差大于100 K,表明制冷机冷端换热器效率不足. 如图9所示为冷却过程中制冷机冷端换热器的对流传热系数变化曲线,最大对流传热系数Kmax<350 W/(m2·K). 图9中,氦气温度越低黏度越小,导致雷诺数越大,所以对流传热系数会随冷却的进行持续增加直至极限值. 制冷机冷端换热对系统性能的影响较大,其效率过低会导致两方面的不利因素,其一是传热效率差,其二是制冷机持续运行于低温区,输出冷量不足.
图 8
图 9
图 9 冷却过程中制冷机冷端对流传热系数变化
Fig.9 Variation of convective heat transfer coefficient of cold end of cryocooler during cooling process
4. 结 论
(1)当前的斯特林制冷机最快可以在73.5 h内将质量为2 t的室温MRI磁体冷却至60 K以下,有较高的冷却效率;
(2)氦气充气压力以及流速对系统效率影响显著,对两者进行优化设计至关重要;
(3)制冷机冷端换热器的性能尚有提升空间,提高其效率可以提高冷却初始阶段制冷机的运行温区,增大冷量输出,减小冷量损耗,进一步加快磁体冷却;
(4)当前计算结果基于一维模型得出,为了更准确、深入地研究系统性能特性,后续须进一步展开数值模拟以及实验验证.
参考文献
MRI磁体技术的发展历程及展望
[J].DOI:10.3969/j.issn.1674-1633.2013.10.002 [本文引用: 1]
Development and recent progress of MRI magnet technology
[J].DOI:10.3969/j.issn.1674-1633.2013.10.002 [本文引用: 1]
超导MRI磁体无液氦改造探讨
[J].
The discussion of superconducting MRI magnet transformation without LHe
[J].
Development of a superconducting bulk magnet for NMR and MRI
[J].DOI:10.1016/j.jmr.2015.07.012 [本文引用: 1]
脉管制冷用于低温超导磁体冷却的可行性分析
[J].
Possibility of pulse tube refrigeration for low-temperature superconducting magnets
[J].
Advances in high power Stirling-type pulse tube cooler
[J].DOI:10.1109/TASC.2010.2041345 [本文引用: 1]
Design concepts for a mechanically refrigerated 13 K superconducting magnet system
[J].DOI:10.1109/TMAG.1983.1062538 [本文引用: 1]
Con-struction of the cryogen-free 23 T hybrid magnet
[J].DOI:10.1109/TASC.2002.1018492 [本文引用: 1]
A cryocooer-cooled 19 T superconducting magnet with 52 mm room temperature bore
[J].
Performance of a cryogen-free 30 T-class hybrid magnet
[J].
Experimental investigation of cooling capacity of 4 K GM cryocoolers in magnetic fields
[J].DOI:10.1016/j.phpro.2015.06.061 [本文引用: 1]
Solid-cryogen cooling technique for superconducting magnets of NMR and MRI
[J].DOI:10.1016/j.phpro.2012.06.303 [本文引用: 1]
A 5 T persistent current niobium-titanium magnet with a 4 K pulse tube cryocooler
[J].DOI:10.1088/0953-2048/17/5/009 [本文引用: 1]
Vertical access zero boil off frampable superconducting magnet system with horizontal field for semicon ductor crystal growth
[J].DOI:10.1109/TASC.2003.812856 [本文引用: 1]
Cool-down characteristic of conduction-cooled superconducting magnet by a cryocooler
[J].
Optimal cool-down time of a 4 K superconducting magnet cooled by a two-stage cryocooler
[J].DOI:10.1016/j.cryogenics.2011.10.002
Development of the active magnetic regenerative refrigerator operating between 77 K and 20 K with the conduction cooled high temperature superconducting magnet
[J].DOI:10.1016/j.cryogenics.2017.09.008 [本文引用: 1]
Cryogen-free HTS coil placed in a heat-exchange gas
[J].DOI:10.1016/S0011-2275(02)00037-1 [本文引用: 1]
Performance of nitrogen heat tubes in cooling down of superconducting magnets
[J].DOI:10.1016/j.phpro.2016.11.016 [本文引用: 1]
Tests on a 6 T conduction-cooled superconducting magnet
[J].DOI:10.1109/TASC.2006.873331 [本文引用: 1]
制冷机传导冷却的超导磁体冷却系统研究进展
[J].
Advance in cryogenic system of cryocooled super-conducting magnet
[J].
传导冷却型低温超导磁体系统的设计与实验
[J].DOI:10.3969/j.issn.1000-6516.2015.02.006 [本文引用: 1]
Design and experiment of conduction cooled superconducting magnet system
[J].DOI:10.3969/j.issn.1000-6516.2015.02.006 [本文引用: 1]
大功率斯特林制冷机的整机数值模拟
[J].DOI:10.3969/j.issn.1000-6516.2014.03.006 [本文引用: 1]
Numerical simulation of a high power Stirling cryocooler
[J].DOI:10.3969/j.issn.1000-6516.2014.03.006 [本文引用: 1]
液氮温区大冷量斯特林制冷机优化研究
[J].
Optimization study on high cooling capacity Stirling cryocooler working on liquid nitrogen temperature
[J].
New equations for heat mass transfer in turbulent pipe and channel flows
[J].
Laminar flow forced convection in ducts
[J].