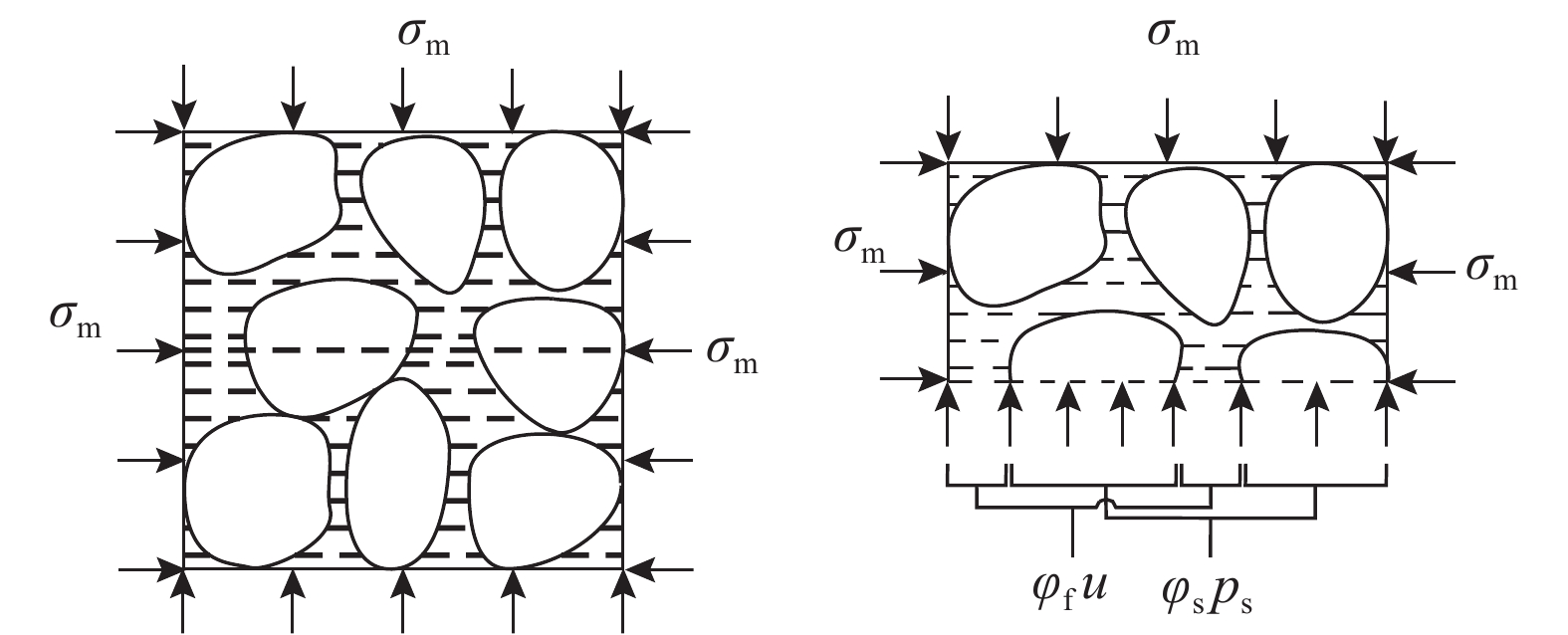
作为多孔介质的饱和岩土体是边坡、桥隧、道路、水利和海洋工程等领域构筑物地基和基础的天然结构材料，其工程性质直接影响构筑物及其围岩的正常使用和安全稳定. 岩土体的本构关系在岩土工程中具有重要意义，Terzaghi^[1]根据土工试验发现有效应力是决定饱和土固相变形与强度的唯一应力状态变量，有效应力原理成为土力学研究的理论基础；Biot^[2]指出当饱和多孔介质的固相基质变形（在土力学中称为土颗粒变形，在岩体力学中称为完整岩块变形）不能忽略时，采用Terzaghi有效应力来表征多孔固相力学特性会产生较大偏差，须对Terzaghi有效应力公式的孔压进行折减，该折减系数被称为Biot系数；Skempton^[3]将摩擦角、剪切抗力角、面积比以及固相基质体积模量和固体骨架体积模量等力学参数引入Biot系数公式，分别针对应力应变关系和强度问题提出2种不同的有效应力表达式；Mitchell^[4]提出考虑物理-化学作用的有效应力表达式，用于处理海底采油引起的地面沉降问题. 以上理论均采用单一的有效应力变量表征岩体变形，将固相基质体变形、摩擦角和物理-化学作用等影响因素归纳到有效应力公式中而得到形式不一的有效应力表达式，其使用条件不尽相同，普适性极大受限. 国内学者对Terzaghi有效应力的力学机理和适用性也进行了诸多深入研究^[5-8]，其中的明显差异促使陈愈炯^[9]整理分析前人众多试验数据资料，从试验的角度证明Terzaghi有效应力公式均适用于饱和砂土和黏土，黏土中的结合水不会对Terzaghi有效应力公式的有效性产生影响.

为了更深刻地认识有效应力，本研究从具有普适性的机械变形功以及饱和多孔介质混合物理论新视角出发，从理论角度重新探索Terzaghi有效应力原理的力学机理和适用范围，揭示饱和多孔介质力学的受力变形规律，以加深对Terzaghi有效应力原理的理解，推动饱和多孔介质本构理论的研究发展.

为了确保概念清晰和统一，防止歧义，首先对几个术语作如下解释. 1）饱和多孔介质作为混合物，是由互不混溶的固流两相混合而成的复杂介质，其中由多孔固相构成固相骨架，没有固相的孔隙由流相全部占有. 在饱和多孔介质中，固相和流相组分存在2种形态：一种是固流组分自身以单一物质形式客观存在的细观真实构形，简称为固相基质和流相基质；另一种是根据平均化理论^[10-11]，将固流组分按照体积分数平均化到整个混合物上的宏观连续构形，是理想化地充盈于整个混合物所占空间体积的形态，简称为固相或流相，其中，某组分的体积分数等于真实构形所占体积与整个混合物所占体积之比. 2）参照混合物理论，将组分的宏观连续构形发生的变形称为组分变形. Geertsma等^[12-13]将组分细观真实构形变形称为组分基质变形；组分体积分数变化所引起的变形称为组分体积分数变形. 3）以饱和土为例，在土力学中通常以“土颗粒”表示固相基质，以“孔隙水”表示流相基质，将平均化后的固相，即表观的“饱和土”占据的空间体积作为整个土体介质的参考构型，其变形称为固相变形；以饱和岩体为例，在岩体力学中通常以“完整岩块”表示固相基质，以“裂隙水”表示流相基质，以平均化后的固相，即表观的“饱和岩体”占据的空间体积作为整个岩体介质的参考构型，其变形称为固相变形. 土体和岩体的最大不同之处在于，土体可以忽略固相基质变形，而岩体须考虑固相基质变形. 应当特别注意区分固相与固相基质2个概念.

假定固流两相基质的变形可以忽略，根据土力学理论可知，固相体应变由孔隙比变化表征，而孔隙比的变化也是固相体积分数变化的另一种反映. 与土力学一致，以平均化后的固相作为饱和多孔介质的参考构形. 根据饱和多孔介质中固流两相的连续性条件可知，固相体积变化等于流相基质从固相中的流出体积，也等于饱和多孔介质的体积变化.

设孔隙比为e的饱和多孔介质单元体所受的总球应力为σ_m，流相基质所承受的球应力即孔压为u，将导致孔隙比变化的应力定义为有效应力 $ \sigma_{\rm{m}}^{'} $，并假定 $ \sigma_{\rm{m}}^{'} $的表达式未知. V为单元体体积，以平均化后的固相作为饱和多孔介质的参考构形，故固相的体积为V. 类似于结构力学中的虚位移分析^[14]，在σ_m作用下，假设单元体内孔隙比e发生大小为δe的虚孔隙变化，按照孔隙体应变定义，单元体的孔隙虚体应变增量为δε_p=δe/（1+e）. 由于不考虑固相基质的变形，单元体固相的虚体积变化量为δε_pV. 单元体受力变形如图1、2所示.

饱和多孔介质表观体积变形对应的总球应力所做的虚体积功为

(1) ${W_{{\sigma _{\rm{m}}}}}{\rm{ = }}{\sigma _{\rm{m}} }{\text δ} {\varepsilon _{\rm{p}}}V.$

有效应力导致孔隙比变化，所做的虚体积功为

(2) ${W_{{{\sigma '}_{\rm{\!\!\! m}}}}}{\rm{ = }}{\sigma '_{\rm{m}} }{\text δ} {\varepsilon _{\rm{p}}}V.$

流相基质压力u所做的虚体积功为

(3) ${W_u}{\rm{ = }}u{\text δ} {V_{\rm{f}}}.$

式中：δV_f为流相基质流出的体积. δV_f与固相体积变化量相等，即

(4) ${\text δ}{V_{\rm{f}}}{\rm{ = }}{\text δ}{\varepsilon _{\rm{p}}}V.$

根据虚功原理可知，对于满足变形协调的虚变形，外力所做虚功等于内力所做虚功，即

(5) ${W_{{\sigma _{\rm{m}}}}}{\rm{ = }}{W_{{{\sigma '}_{\rm{\!\!\!\! m}} }}} + {W_u}.$

将式（1）~（4）代入式（5），可得

(6) ${\sigma _{\rm{m}} }{\text δ} {\varepsilon _{\rm{p}}}V = {\sigma '_{\rm{m}} }{\text δ} {\varepsilon _{\rm{p}}}V + u{\text δ} {\varepsilon _{\rm{p}}}V.$

约去相同项δε_pV并整理，可得有效应力的表达式为

(7) ${\sigma '_{\rm{m}} } = {\sigma _{\rm{m}} } - u.$

式（7）证明，当不考虑固流两相基质变形时，Terzaghi有效应力公式完全适用于饱和多孔介质，无须对其进行修正.

对于存在流相基质渗流的情况，设固流两相基质的速度矢量分别为v_s、v_f，流相体积分数为 $ \varphi_{{\rm{f}}} $. 以固相作为饱和多孔介质的参考构形，则流相基质相对固相基质现时位置的扩散速度为

(8) ${{w}_{\rm{f}}} = {{v}_{\rm{f}}} - {{v}_{\rm{s}}}.$

当固流两相基质的变形可以忽略时，对于空间中体积为V的任意固定单元体，其内部的固流两相基质总体积变化量为零. 假设A为单元体的表面积，dA为A界面上的面元，n为该面元单位法向上的方向矢量，有^[15]

(9) $\int_A {\left[ {{\varphi _{\rm{f}}}{{v}_{\rm{f}}} + \left( {1 - {\varphi_{\rm{f}}}} \right){{v}_{\rm{s}}}} \right]} \cdot {n} {\rm{d}}A = 0.$

对式（9）进行高斯转换，并结合式（8），可得

(10) $\begin{split} \int_V {{\rm{div}}\; \left[ {{\varphi_{\rm{f}}}{{v}_{\rm{f}}} + \left( {1 - {\varphi_{\rm{f}}}} \right){{v}_{\rm{s}}}} \right]} {\rm{d}}V = \int_V {{\rm{div}}\; \left( {{\varphi_{\rm{f}}}{{w}_{\rm{f}}} + {{v}_{\rm{s}}}} \right)} {\rm{d}}V = 0. \end{split}$

由于被积函数连续，而单元体又是任取的，因此式（10）要成立须满足被积函数恒等于零，即

(11) ${\rm{div}}\; \left( {{\varphi_{\rm{f}}}{{w}_{\rm{f}}} + {{v}_{\rm{s}}}} \right) = {\rm{div}}\; \left( {{\varphi_{\rm{f}}}{{w}_{\rm{f}}}} \right) + {\rm{di}}{{\rm{v}}\;_{}}{{v}_{\rm{s}}} = 0.$

在一般的岩土工程渗流问题中，实际分析和计算采用表观的出逸流速 $ {{w}}_{\rm{f}}^{'} = {{\varphi}}_{{\rm{f}}}{{w}}_{{\rm{f}}}$. 饱和多孔介质体积应变率为E′=div v_s. 孔隙流体在介质中所受到的单位体积摩擦阻力矢量f=grad u. 单位时间单元体所受外力做功包括体积变形功W₁及渗流水压力功W₂，结合式（11）有

(12) ${W_1} = \int_V {{\sigma _{\rm{m}} }E'} { \rm{d}}V = \int_V {{\sigma _{\rm{m}} }{\rm{di}}{{\rm{v}}\;_{}}{{v}_{\rm{s}}}} {\rm{d}}V,$

(13) $\begin{split} {W_2} = & \int_A {u{{{w}}_{\rm{f}}^{'}} \cdot } {n}\;{\rm{d}}A = \int_V {{\rm{div}}\;\left( {u{\varphi_{\rm{f}}}{{w}_{\rm{f}}}} \right)} {\rm{d}}V = \\ & \int_V {u{\rm{div}}\;\left( {{\varphi_{\rm{f}}}{{w}_{\rm{f}}}} \right)} {\rm{d}}V + \int_V ({{\rm{gra}}{{\rm{d}}\;_{}}u) \cdot \left( {{\varphi_{\rm{f}}}{{w}_{\rm{f}}}} \right)} {\rm{d}}V{\rm{ = }}\\ & \int_V {\left[ { - u{\rm{di}}{{\rm{v}}\;_{}}{{v}_{\rm{s}}} + ({\rm{gra}}{{\rm{d}}\;_{}}u) \cdot \left( {{\varphi_{\rm{f}}}{{w}_{\rm{f}}}} \right)} \right]} {\rm{d}}V. \end{split}$

在单位时间内单元体内力所做功包括有效应力做功W₃及流相基质所受摩擦阻力做功W₄，表达式分别为

(14) ${W_3} = \int_V {{{\sigma}_{\rm{m}}^{'} } E{\text{′}}} {\rm{d}}V = \int_V {{{\sigma}_{\rm{m}}^{'} }{\rm{di}}{{\rm{v}}\;_{}}{{{v}}_{\rm{s}}}} {\rm{d}}V,$

(15) ${W_4} = \int_V {{{f}} \cdot {{{{w}}}_{\rm{f}}^{'}}} {\rm{d}}V = \int_V ({{\rm{gra}}{{\rm{d}}_{}}\;u) \cdot \left( {{\varphi_{\rm{f}}}{{{w}}_{\rm{f}}}} \right)} {\rm{d}}V.$

根据功能原理有

(16) ${W_1} + {W_2} = {W_3} + {W_4}.$

将式（12）~（15）代入式（16），可得

(17) $\begin{split} & \int_V {{\sigma _{\rm{m}}}{\rm{di}}{{\rm{v}}\;_{}}{{v}_{\rm{s}}}} {\rm{d}}V + \int_V {\left[ { - u{\rm{di}}{{\rm{v}}\;_{}}{{v}_{\rm{s}}} + ({\rm{gra}}{{\rm{d}}\;_{}}u) \cdot \left( {{\varphi_{\rm{f}}}{{w}_{\rm{f}}}} \right)} \right]} {\rm{d}}V = \\ & \quad\quad \int_V {{{\sigma '}_{\rm{\!\!\! m}}}{\rm{di}}{{\rm{v}}\;_{}}{{v}_{\rm{s}}}} {\rm{d}}V + \int_V ({{\rm{gra}}{{\rm{d}}\;_{}}u) \cdot \left( {{\varphi_{\rm{f}}}{{w}_{\rm{f}}}} \right)} {\rm{d}}V.\qquad\quad\,\,\,\,\,\,(17) \end{split}$

即

(18) $ \int_V {\left( {{\sigma _{\rm{m}} } - u - {{\sigma '}_{\rm{\!\!\!\! m}} }} \right){\rm{di}}{{\rm{v}}\;_{}}{{{v}}_{\rm{s}}}} {\rm{d}}V = 0.$

同理，上式要成立须满足被积函数恒等于零，于是得到式（7）. 综上所述，当不考虑固流两相基质变形时，即使存在流相基质渗流，Terzaghi有效应力公式也完全适用于饱和多孔介质，无须对其进行修正.

假定饱和多孔介质的固流两相之间不存在化学反应等质量交换. 设α为组分名称变量，α $ \in \{{\rm s},\;{\rm f}\}$，s表示固相，f表示流相. ρ_rα为α组分真实密度，ρ_α= $\varphi $_αρ_rα为α组分相密度， $\varphi $_α为α组分体积分数. 对于饱和多孔介质，体积分数满足

(19) ${\varphi_{\rm{s}}} + {\varphi_{\rm{f}}} = 1.$

式中： $\varphi _{\rm s}$ 为固相体积分数.

设σ_sm、σ_fm分别为混合物理论中固流两相承受的Cauchy球应力； $ p_{\rm s} = \sigma_{\rm sm}/\varphi_{\rm s}$ 为固相基质承受的球应力，简称固相基质压力； $ u = \sigma_{\rm fm}/\varphi_{\rm f}$ 为流相基质承受的球应力，等于孔隙流体压力^[13]，简称流相基质压力或孔压。单元体受力如图3所示. 根据混合物理论有^[16]

(20) ${\sigma _{\rm{m}}} = {\sigma _{{\rm{sm}}}} + {\sigma _{{\rm{fm}}}} = {\varphi_{\rm{s}}}{p_{\rm{s}}} + {\varphi_{\rm{f}}}u.$

设在初始时刻t₀时，固相和流相组分所占的真实体积分别为V_rs0、V_rf0，体积分数分别为 $ \varphi_{{\rm{s}}0} $、 $ \varphi _{{\rm{f}}0}$，混合物的总体积为V₀=V_rs0+V_rf0. 按体积分数平均化后固相体积为 $ V_{{\rm{s}}0} = V_{{\rm{rs}}0}/\varphi_{{\rm{s}}0}$，流相体积为 $ V_{{\rm{f}}0} = V_{{\rm{rf}}0}/ \varphi_{{\rm{f}}0}$. 固流两相在各自应力的作用下在 $t$ 时刻体积分别变为V_s、V_f. 混合物中流相基质在多孔固相中存在渗流运动，部分流体从骨架孔隙中流入或流出，因此在t时刻V_s一般不等于V_f.

设固相体应变和流相体应变分别为ε_sv、ε_fv，由于变形前后的组分质量保持不变，即m_s=m_s0，m_f=m_f0. 由于混合物理论是按平均化后的组分体积来定义组分体应变的，有^[16]

(21) ${\varepsilon _{{\rm{sv}}}} = - \ln\; {{{(V_{\rm{s}}}}/{{V_{{\rm{s}}0}}}}) = - \ln\; \frac{{{{{m_{\rm{s}}}}/{{\rho _{\rm{s}}}}}}}{{{{{m_{{\rm{s}}0}}}/{{\rho _{{\rm{s}}0}}}}}} = \ln\; {{{(\rho _{\rm{s}}}}/{{\rho _{{\rm{s}}0}}}}),$

(22) ${\varepsilon _{{\rm{fv}}}} = - \ln \;{{{(V_{\rm{f}}}}/{{V_{{\rm{f}}0}}}}) = - \ln \;\frac{{{{{m_{\rm{f}}}}/{{\rho _{\rm{f}}}}}}}{{{{{m_{{\rm{f}}0}}}/{{\rho _{{\rm{f}}0}}}}}} = \ln\; ({{{\rho _{\rm{f}}}}/{{\rho _{{\rm{f}}0}}}}).$

式中：ρ_s0、ρ_f0分别为初始时刻固相、液相密度.

将 $ \rho_{{\rm{s}}} = \varphi_{{\rm{s}}} \rho_{{\rm{rs}}}$、 $ \rho_{{\rm{f}}} = \varphi_{{\rm{f}}} \rho_{{\rm{rf}}}$、 $ \varphi_{{\rm{s}}} = 1/(1+e)$ 分别代入式（21）~（22），可得

(23) $ \begin{split} {\varepsilon _{{\rm{sv}}}} = & \ln\; ({\rho _{\rm{s}}}/{\rho _{{\rm{s0}}}} )= \ln \;[({\varphi_{\rm{s}}}{\rho _{{\rm{rs}}}})/({\varphi_{{\rm{s}}0}}{\rho _{{\rm{rs}}0}}) ]= \\ & - \ln \;[(1 + e)/(1 + {e_0})] + \ln \;({\rho _{{\rm{rs}}}}/{\rho _{{\rm{rs}}0}}), \end{split}$

(24) $\begin{split} {\varepsilon _{{\rm{fv}}}} = & \ln \;({\rho _{\rm{f}}}/{\rho _{{\rm{f0}}}}) = \ln \;[ \left( {{\varphi_{\rm{f}}}{\rho _{{\rm{rf}}}}} \right)/\left( {{\varphi_{{\rm{f}}0}}{\rho _{{\rm{rf}}0}}} \right)]{\rm{ = }}\\ & \ln \;({\varphi_{\rm{f}}}/{\varphi_{{\rm{f}}0}}) + \ln \;({\rho _{{\rm{rf}}}}/{\rho _{{\rm{rf}}0}}). \end{split}$

式中：ρ_rs0、ρ_rf0分别为初始时刻固相、液相真实密度.

根据式（23），将固相体积分数变化引起的固相体应变定义为固相体积分数应变，表达式^[17]为

(25) ${\varepsilon _{{\rm{sf}}}} = - \ln \;[{{\left( {1 + e} \right)}/{\left( {1 + {e_0}} \right)}}] = \ln \;[{{\left( {1 + {e_0}} \right)}/{\left( {1 + e} \right)}}].$

设固流两相基质真实构形的初始体积V_rs0、V_rf0，在真实应力作用下变化为V_rs、V_rf. 若以压为正，根据连续介质力学理论，固流两相基质体应变的表达式^[18]分别为

(26) ${\varepsilon _{{\rm{rsv}}}} = - \ln \; ({{{V_{{\rm{rs}}}}}/{{V_{{\rm{rs}}0}}}}) = \ln\; ({{{\rho _{{\rm{rs}}}}}/{{\rho _{{\rm{rs}}0}}}}),$

(27) ${\varepsilon _{{\rm{rfv}}}} = - \ln\; ({{{V_{{\rm{rf}}}}}/{{V_{{\rm{rf}}0}}}}) = \ln\; ({{{\rho _{{\rm{rf}}}}}/{{\rho _{{\rm{rf}}0}}}}).$

联立式（23）、（25）、（26），可得

(28) ${\varepsilon _{{\rm{sv}}}} = {\varepsilon _{{\rm{sf}}}} + {\varepsilon _{{\rm{rsv}}}}.$

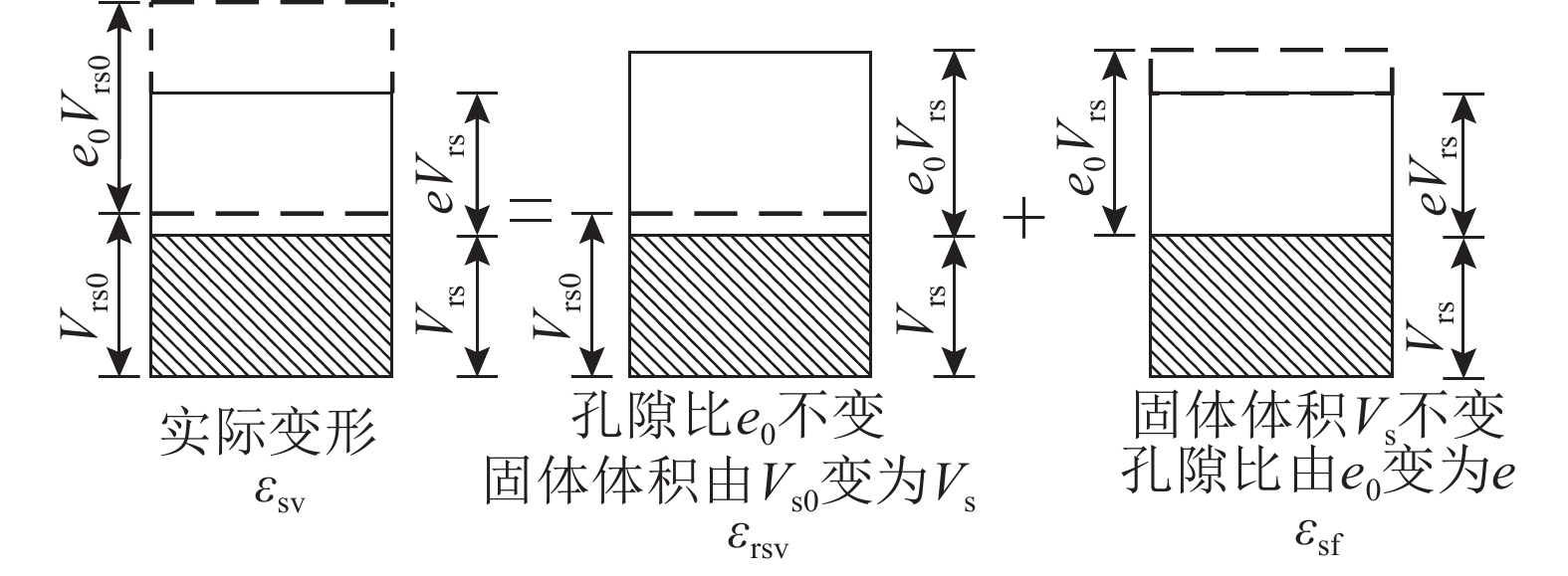
根据式（25）、（26）、（28），固相体应变可分解为固相基质体应变和固相体积分数应变，如图4所示.

对式（21）~（27）求时间的导数，可得

(29) $\mathop \varepsilon \limits^.{_{\rm{sf}}}= - {{\mathop e\limits^. }/{\left( {1 + e} \right)}},$

(30) $\mathop \varepsilon \limits^. {_{{{\rm{sv}}}}} = {\mathop \varphi \limits^. {_{\rm{s}}}}/{\varphi_{\rm{s}}} + {\mathop \rho \limits^. { _{\rm{rs}}}}/{\rho _{{\rm{rs}}}} = - \mathop e\limits^. /\left( {1 + e} \right) + {\mathop \rho \limits^. {_{\rm{rs}}}}/{\rho _{{\rm{rs}}}},$

(31) $\begin{split} \mathop \varepsilon \limits^.{_{{{\rm{fv}}}}} = & {\mathop \varphi \limits^. {_{\rm{f}}}}/{\varphi_{\rm{f}}} + {\mathop \rho \limits^. {_{\rm{rf}}}}/{\rho _{{\rm{rf}}}} = \mathop e\limits^. /\left[ {e(1 + e)} \right] + {\mathop \rho \limits^. {_{\rm{rf}}}}/{\rho _{{\rm{rf}}}} = \\ & {\varphi_{\rm{s}}}\mathop e\limits^. /\left[ {{\varphi_{\rm{f}}}(1 + e)} \right] + {\mathop \rho \limits^. { _{\rm{rf}}}}/{\rho _{{\rm{rf}}}}, \end{split}$

(32) $\mathop \varepsilon \limits^.{_{{{\rm{rsv}}}}} = {{{{\mathop \rho \limits^. }_{{\rm{rs}}}}}/{{\rho _{{\rm{rs}}}}}},$

(33) $\mathop \varepsilon \limits^.{_{{{\rm{rfv}}}}} = {{{{\mathop \rho \limits^. }_{{\rm{rf}}}}}/{{\rho _{{\rm{rf}}}}}}.$

由式（28）、式（30）~（33）可得

(34) $\mathop \varepsilon \limits^.{_{{{\rm{sv}}}}} = \mathop \varepsilon \limits^.{_{{{\rm{sf}}}}} + \mathop \varepsilon \limits^.{_{{{\rm{rsv}}}}} ,$

(35) $\mathop \varepsilon \limits^.{_{{{\rm{fv}}}}} = - \varphi _{{\rm{s}}}\mathop \varepsilon \limits^.{_{{{\rm{sf}}}}}/\varphi_{{\rm{f}}} + \mathop \varepsilon \limits^.{_{{{\rm{rfv}}}}} .$

根据混合物理论^{[13, 16]}，饱和多孔介质体积变形功率为固、流相组分Cauchy球应力与体应变率乘积之和. 根据固相基质压力的定义有固相Cauchy球应力 $ \sigma _{{\rm{sm}}} = \varphi_{{\rm{s}}} p_{{\rm{s}}}$；根据孔隙流体压力的定义有流相Cauchy球应力 $ \sigma_{{\rm{fm}}} = \varphi_{{\rm{f}}}u $，所以总体积变形功率表达式为

(36) $\mathop W\limits^. = {\varphi_{\rm{s}}}{p_{\rm{s}}}\mathop \varepsilon \limits^.{_{{{\rm{sv}}}}} + {\varphi_{\rm{f}}}u\mathop \varepsilon \limits^.{_{{{\rm{fv}}}}} .$

将式（34）、（35）代入式（36），并利用式（19）、（20），可得

(37) $\begin{split} \mathop W\limits^. = & {\varphi_{\rm{s}}}{p_{\rm{s}}}\mathop \varepsilon \limits^.{_{{{\rm{sv}}}}} + {\varphi_{\rm{f}}}u\mathop \varepsilon \limits^.{_{{{\rm{fv}}}}} = \\ & {\varphi_{\rm{s}}}{p_{\rm{s}}}\left( {\mathop \varepsilon \limits^.{_{{{\rm{sf}}}}} + \mathop \varepsilon \limits^.{_{{{\rm{rsv}}}}} } \right) + {\varphi_{\rm{f}}}u\left( { - {\varphi_{\rm{s}}}\mathop \varepsilon \limits^.{_{{{\rm{sf}}}}} /{\varphi_{\rm{f}}} + \mathop \varepsilon \limits^.{_{{{\rm{rfv}}}}} } \right) = \\ & {\varphi_{\rm{s}}}{p_{\rm{s}}}\mathop \varepsilon \limits^.{_{{{\rm{rsv}}}}} + {\varphi_{\rm{f}}}u\mathop \varepsilon \limits^.{_{{{\rm{rfv}}}}} + {\varphi_{\rm{s}}}{p_{\rm{s}}}\mathop \varepsilon \limits^.{_{{{\rm{sf}}}}} - \left( {1 - {\varphi_{\rm{f}}}} \right)u\mathop \varepsilon \limits^.{_{{{\rm{sf}}}}} = \\ & {\varphi_{\rm{s}}}{p_{\rm{s}}}\mathop \varepsilon \limits^.{_{{{\rm{rsv}}}}} + {\varphi_{\rm{f}}}u\mathop \varepsilon \limits^.{_{{{\rm{rfv}}}}} + \left( {{\varphi_{\rm{s}}}{p_{\rm{s}}} + {\varphi_{\rm{f}}}u - u} \right)\mathop \varepsilon \limits^.{_{{{\rm{sf}}}}} = \\ & {\varphi_{\rm{s}}}{p_{\rm{s}}}\mathop \varepsilon \limits^.{_{{{\rm{rsv}}}}} + {\varphi_{\rm{f}}}u\mathop \varepsilon \limits^.{_{{{\rm{rfv}}}}} + \left( {{\sigma _{\mathop{\rm m}\nolimits} } - u} \right)\mathop \varepsilon \limits^.{_{{{\rm{sf}}}}} . \end{split}$

式（37）表明，固流两相所受的基质压力与基质体应变为功共轭对；应力σ_m−u与固相体积分数应变为功共轭对. 定义与固相体积分数应变成功共轭对的应力为有效应力 $ \sigma_{\rm{m}}^{'}$，则有 $ \sigma_{\rm{m}}^{'}$=σ_m−u，即为Terzaghi有效应力. 将 $ \sigma_{\rm{m}}^{'}$=σ_m−u代入式（37），可得

(38) $\mathop W\limits^. = {\varphi_{\rm{s}}}{p_{\rm{s}}}\mathop \varepsilon \limits^.{{_{{\rm{rsv}}}}} + {\varphi_{\rm{f}}}u\mathop \varepsilon \limits^.{{_{{\rm{rfv}}}}} + {\sigma '_{\rm{m}}}\mathop \varepsilon \limits^.{{_{{\rm{sf}}}}} .$

式（38）表明，饱和多孔介质混合物的总体积变形功等于固流两相基质体积变形功与固相体积分数变形功之和.

假定饱和多孔介质单位质量的变形功由3个部分组成，第1部分是固相单位密度内所含的固相细观变形引起的变形功W_rs，只与ε_rsv相关；第2部分是流相单位质量内所含的流相细观变形引起的变形功W_rf，只与ε_rfv相关；第3部分是固相单位密度内所含的固相体积分数变化引起的变形功W_sf，只与ε_sf有关. 根据混合物理论^{[13, 16]}，有

(39) $\mathop W\limits^. = {\rho _{\rm{s}}}\mathop W\limits^.{ {{_{{\rm{rs}}}}} } + {\rho _{\rm{f}}}\mathop W\limits^.{ {{_{{\rm{rf}}}}} } + {\rho _{\rm{s}}}\mathop W\limits^.{{{_{{\rm{sf}}}}} } .$

将式（39）代入式（38），并利用公式 $\;\rho _{{\rm{s}}} = \varphi_{{\rm{s}}} \rho_{{\rm{rs}}}$ 和 $\;\rho _{{\rm{f}}} = \varphi_{{\rm{f}}} \rho_{{\rm{rf}}}$，根据变量ε_rsv、ε_rfv、ε_sf相互独立的性质，通过求偏导处理，可得

(40) ${{{p_{\rm{s}}}}/{{\rho _{{\rm{rs}}}}}} = {{\partial {W_{{\rm{rs}}}}}/{\partial {\varepsilon _{{\rm{rsv}}}}}},$

(41) ${u/{{\rho _{{\rm{rf}}}}}} = {{\partial {W_{{\rm{rf}}}}}/{\partial {\varepsilon _{{\rm{rfv}}}}}},$

(42) ${{\sigma {'_{\rm{m}}}}/{{\rho _{\rm{s}}}}} = {{\partial {W_{{\rm{sf}}}}}/{\partial {\varepsilon _{{\rm{sf}}}}}}.$

将式（21）、（26）~（28）代入式（40）~（42），可得

(43) ${p_{\rm{s}}} = {\rho _{{\rm{rs0}}}}\exp \;({\varepsilon _{{\rm{rsv}}}})\left[ {{{\partial {W_{{\rm{rs}}}}}/{\partial {\varepsilon _{{\rm{rsv}}}}}}} \right],$

(44) $u = {\rho _{{\rm{rf0}}}}\exp \;({\varepsilon _{{\rm{rfv}}}})\left[ {{{\partial {W_{{\rm{rf}}}}}/{\partial {\varepsilon _{{\rm{rfv}}}}}}} \right],$

(45) $\sigma {'_{\rm{m}}} = {\rho _{{\rm{s0}}}}\exp\; ({\varepsilon _{{\rm{rsv}}}})\exp\; ({\varepsilon _{{\rm{sf}}}})\left[ {{{\partial {W_{{\rm{sf}}}}}/{\partial {\varepsilon _{{\rm{sf}}}}}}} \right].$

式中：ρ_rs0、ρ_rf0、ρ_s0为常量. 式（43）、（44）表明，固相基质体应变唯一地决定固相基质压力；流相基质体应变唯一地决定流相基质压力即孔压，反之亦然. 式（42）表明，固相体积分数应变唯一地决定固相单位密度的Terzaghi有效应力，反之亦然. 式（45）进一步表明，Terzaghi有效应力本身须根据固相体积分数应变和固相基质体应变两者共同决定，其中固相体积分数应变为主要因素. 在小应变条件下，当方程中存在比 $\varphi $_α $-\varphi $_α0、e₀$- e $、 $\rho$_α $-\rho$_α0、 $\rho$_rα $-\rho$_rα0低一阶的无穷小量时， $\varphi $_α $-\varphi $_α0、e₀$- e $、 $\rho$_α $-\rho$_α0、 $\rho$_rα $-\rho$_rα0作为高次项可以略去，因此在小应变条件下，由式（20）、（28）、（35）可得

(46) ${\sigma _{\rm{m}}} = {\varphi_{{\rm{s}}0}}{p_{\rm{s}}} + {\varphi_{{\rm{f}}0}}u,$

(47) ${\varepsilon _{{\rm{sv}}}} = {\varepsilon _{{\rm{sf}}}} + {\varepsilon _{{\rm{rsv}}}},$

(48) ${\varepsilon _{{\rm{fv}}}} = - {{{\varphi_{{\rm{s0}}}}{\varepsilon _{{\rm{sf}}}}}/{{\varphi_{{\rm{f0}}}}}} + {\varepsilon _{{\rm{rfv}}}}.$

同时，在小应变条件下，当方程中存在比 $\varphi $_α $-\varphi $_α0、 $e_0-e$、 $\rho$_α $-\rho$_α0、 $\rho$_rα $-\rho$_rα0高阶的无穷小量时，可将式（49）~（51）进行泰勒展开，并略去高阶无穷小量：

(49) ${\varepsilon _{{\rm{sf}}}} = - \ln \; [\left( {1 + e} \right)/\left( {1 + {e_0}} \right)] \approx \left( {{e_0} - e} \right)/\left( {1 + {e_0}} \right),$

(50) ${\varepsilon _{{\rm{rsv}}}} = \ln \;({\rho _{{\rm{rs}}}}/{\rho _{{\rm{rs0}}}} ) \approx \left( {{\rho _{{\rm{rs}}}} - {\rho _{{\rm{rs}}0}}} \right)/{\rho _{{\rm{rs}}0}},$

(51) ${\varepsilon _{{\rm{rfv}}}} = \ln \; ({\rho _{{\rm{rf}}}}/{\rho _{{\rm{rf0}}}}) \approx \left( {{\rho _{{\rm{rf}}}} - {\rho _{{\rm{rf}}0}}} \right)/{\rho _{{\rm{rf}}0}}.$

式（49）与不考虑固相基质体应变（即不考虑土颗粒体应变）的饱和土力学的固相变形公式^[19]一致. 同时在小应变条件下，ε_rsv、ε_rfv、ε_sf均可视为无穷小量，故有exp （ε_rsv）≈1，exp （ε_rfv）≈1，exp （ε_sf）≈1，式（43）~（45）可改写为

(52) ${p_{\rm{s}}} = {{\partial ({\rho _{{\rm{rs0}}}}{W_{{\rm{rs}}}})}/{\partial {\varepsilon _{{\rm{rsv}}}}}},$

(53) $u = {{\partial ({\rho _{{\rm{rf0}}}}{W_{{\rm{rf}}}})}/{\partial {\varepsilon _{{\rm{rfv}}}}}},$

(54) $\sigma {'_{\rm{m}}} = {{\partial ({\rho _{{\rm{s0}}}}{W_{{\rm{sf}}}})}/{\partial {\varepsilon _{{\rm{sf}}}}}}.$

式（52）~（54）表明，在小应变条件下，固相基质体应变唯一地决定固相基质压力；流相基质体应变唯一地决定流相基质压力. 固相体积分数应变唯一地决定Terzaghi有效应力，反之亦然. 式（47）表明固相体应变等于固相体积分数应变和固相基质体应变之和，因此固相体应变由Terzaghi有效应力和固相基质压力两者共同决定. 特别地，若忽略固流两相基质的体应变，如饱和土，则有ε_rsv=0、ε_rfv=0、ε_sf=ε_sv，固相单位密度的内能W_s等于固相体积分数变化引起的内能W_sf，固相体应变等于固相体积分数应变，它们直接取决于Terzaghi有效应力。联立式（38）、（39），可得

(55) $\mathop W\limits^. = {\rho _{{\rm{s0}}}}\mathop W\limits^.{{_{{\rm{sf}}}}} = {\sigma '_{\rm{m}}} \mathop \varepsilon \limits^.{{_{{\rm{sf}}}}} = {\sigma '_{\rm{m}}} \cdot \mathop \varepsilon \limits^.{{_{{\rm{sv}}}}} .$

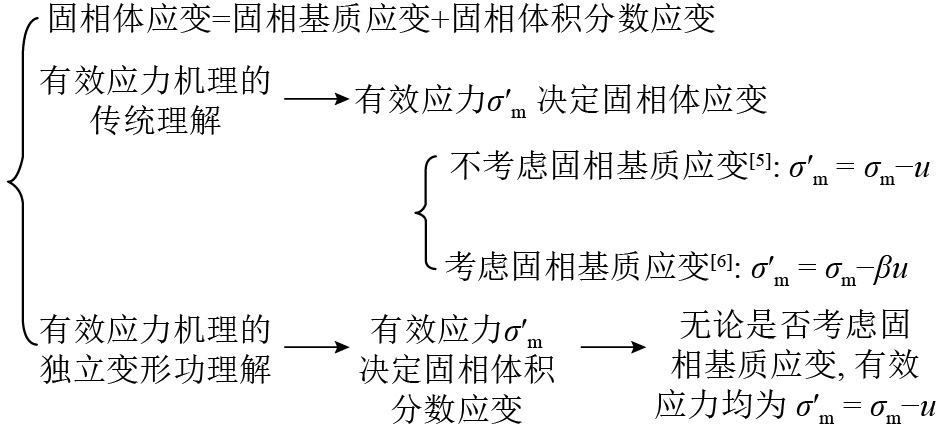
综上所述，完备的饱和多孔介质本构方程除须确定固相应变外，还须同时确定流相应变. 由式（47）~（48）、式（52）~（54）可知，须采用固相基质体应变、固相体积分数应变和流相基质体应变这3个应变变量（或固相基质压力、Terzaghi有效应力和孔隙流体压力这3个应力变量）才能反映小应变条件下饱和多孔介质的全部受力变形性质，如图5所示. 图中，β为Biot系数.

（1）当忽略固流两相基质体应变时，利用机械功原理证明Terzaghi有效应力公式适用性. 在证明过程中，并未针对特定形态和接触状况的固流两相基质，故Terzaghi有效应力公式对包括含结合水的饱和黏土在内的所有饱和土均适用. 这与陈愈炯^[9]的结论一致.

（2）将饱和多孔介质的固相体应变分为固相基质体应变和固相体积分数应变两部分，将有效应力视为固相体积分数应变的功共轭量，由此得到的有效应力公式与Terzaghi有效应力表达式一致，它是具有固定表达式的应力状态变量.

（3）在小应变的条件下，当饱和多孔介质中固流两相基质和固相体积分数的变化作用相互独立时，固相体积分数应变唯一地决定于Terzaghi有效应力. 基于此，Terzaghi有效应力无须根据研究对象和工况进行修正.

（4）把固相单位质量的Terzaghi有效应力视为改变固相体积分数应变的应力，要比传统地把它视为改变固相体应变的应力更能揭示其力学机理. 后种情况仅当忽略固相基质体应变时成立.

（5）同时考虑固相基质压力、Terzaghi有效应力和孔隙流体压力这3个应力变量方能完备地建立饱和多孔介质本构模型.