浙江大学学报(工学版)

浙江大学学报(工学版), 2019, 53(4): 811-818 doi: 10.3785/j.issn.1008-973X.2019.04.023

工程力学

二维十字排列椭圆孔声子晶体带隙研究

高楠,, 李剑, 鲍荣浩,, 陈伟球

Study of band gaps of two-dimensional phononic crystals with criss-crossed elliptical holes

GAO Nan,, LI Jian, BAO Rong-hao,, CHEN Wei-qiu

通讯作者: 鲍荣浩，男，副教授. orcid.org/0000-0002-4442-9533. E-mail： brh@zju.edu.cn

收稿日期: 2018-01-19  

Received: 2018-01-19  

作者简介 About authors

高楠（1994—），女，硕士生，从事声子晶体的研究.orcid.org/0000-0002-4943-7217.E-mail：21624008@zju.edu.cn , E-mail：21624008@zju.edu.cn

摘要

采用有限元及实验方法，研究二维十字排列椭圆孔声子晶体中弹性波传播的带隙以及人为引入的夹杂对带隙的调控. 当声子晶体薄板沿板厚方向均匀施加面内激励时，将激发面内的动力响应，对应于平面应力状态. 基于逆向思维，针对二维十字排列椭圆孔声子晶体薄板，建立平面有限元模型，计算该模型沿晶格ΓX方向的波动传输特性，分析孔洞长短轴之比、孔隙率和线缺陷等因素对带隙及弹性波传播特性的影响. 制作与计算模型同尺寸的声子晶体试样进行传输特性实验，测试结果与有限元仿真结果吻合. 结果表明，带隙的宽度随着椭圆孔长短轴比例的增加而增大，可以通过引入合适的线缺陷来反向调控声子晶体的带隙.

关键词： 声子晶体 ; 十字排列椭圆孔 ; 带隙 ; 弹性波调控

Abstract

The band gaps of elastic wave in two-dimensional phononic crystals with criss-crossed elliptical holes and the tunability of band gaps induced by the artificially introduced inclusions were analyzed through finite element method and experimental method. When the in-plane excitation is uniformly applied along the thickness of a thin phononic crystal plate, the dynamic response of the plate can be approximated as a plane-stress problem. Thin phononic plates with elliptical holes arrayed in a criss-cross pattern were analyzed with a two-dimensional finite element model based on the contrarian thinking in order to calculate the wave transmission along the ΓX direction of the reciprocal lattice. The effects of the ratio of major axis to minor axis, the porosity of holes, and the artificially introduced line defects on the band gaps and the wave propagation characteristics were systematically analyzed. The testing samples with the same dimensions as the numerical models were produced to conduct the transmission experiments. The numerical results accorded well with the experimental results. Results show that the width of band gap enlarges with the increasing of the ratio of major axis to minor axis, and the band gap can be reversely controlled by the insertion of line defects.

Keywords： phononic crystal ; criss-crossed elliptical hole ; band gap ; elastic wave control

PDF (1910KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

高楠, 李剑, 鲍荣浩, 陈伟球. 二维十字排列椭圆孔声子晶体带隙研究. 浙江大学学报(工学版)[J], 2019, 53(4): 811-818 doi:10.3785/j.issn.1008-973X.2019.04.023

GAO Nan, LI Jian, BAO Rong-hao, CHEN Wei-qiu. Study of band gaps of two-dimensional phononic crystals with criss-crossed elliptical holes. Journal of Zhejiang University(Engineering Science)[J], 2019, 53(4): 811-818 doi:10.3785/j.issn.1008-973X.2019.04.023

声子晶体是一种周期复合材料，当声波在其中传播时，可能在某些频率范围内会快速衰减，形成所谓的带隙（band gap）. Sigalas等[1]在研究三维周期点阵结构中弹性波的传播时，首次从理论上证明了带隙的存在. Kushwaha等[2]在研究二维周期复合材料时，借用物理学中的光子晶体，提出弹性波传播中声子晶体的概念.

近年来，具有周期性质的多孔声子晶体受到越来越广泛的关注. 研究表明，孔洞的几何参数对多孔声子晶体的带隙特性有着重要的影响. 例如，Mohammadi等[3]研究圆孔声子晶体板中圆孔半径对整体带隙特性的影响，发现带隙宽度随孔隙率的增大而变宽. Reinke等[4]通过在固/固声子晶体板中开孔的方式，增大了原系统的带隙宽度. Wang等[5]在均匀固体中引进局域共振单元的设计，通过改变共振单元的结构几何参数来调控带隙特性.

目前，计算声子晶体能带结构的方法主要有传递矩阵法[6-7]、平面波展开法[1-2]、多重散射法[8-9]、时域有限差分法[10-11]和有限元方法[12-13]等. 随着声子晶体结构设计的复杂化，有限元法将是最有效也是最有潜力的分析手段[12-13]. 目前，商用有限元软件COMSOL已经开发了带隙和传输谱的专用计算模块. 黄屹澜等[14]基于ABAQUS平台，开发用于分析软声子晶体变形对弹性波传播特性影响的计算模块. 另外，实验扮演着十分重要的角色. 比如，Martinez-Sala等[15]首次从实验角度证实了弹性波带隙的存在；Yang等[16-17]在这方面也作了许多工作.

为了达到宽带隙的目的，基于常规圆孔软材料受压屈曲变形导致构型改变后具有更丰富的带隙特征这一发现[18]，本文将圆孔结构的后屈曲构型简化为十字排列的椭圆孔结构并作为初始构型，探究该构型声子晶体的带隙特性. 具体以二维十字排列椭圆孔声子晶体薄板为例，采用有限元仿真及实验来考察方向带隙特性，讨论几何参数（包括孔洞长短轴之比及孔隙率）及引入线缺陷对声子晶体中弹性波传播的影响. 结合模态分析，进一步研究带隙变化的产生机理. 本文的研究为周期开孔声子晶体的设计和带隙调控提供了新的思路和参考.

1. 有限元模拟

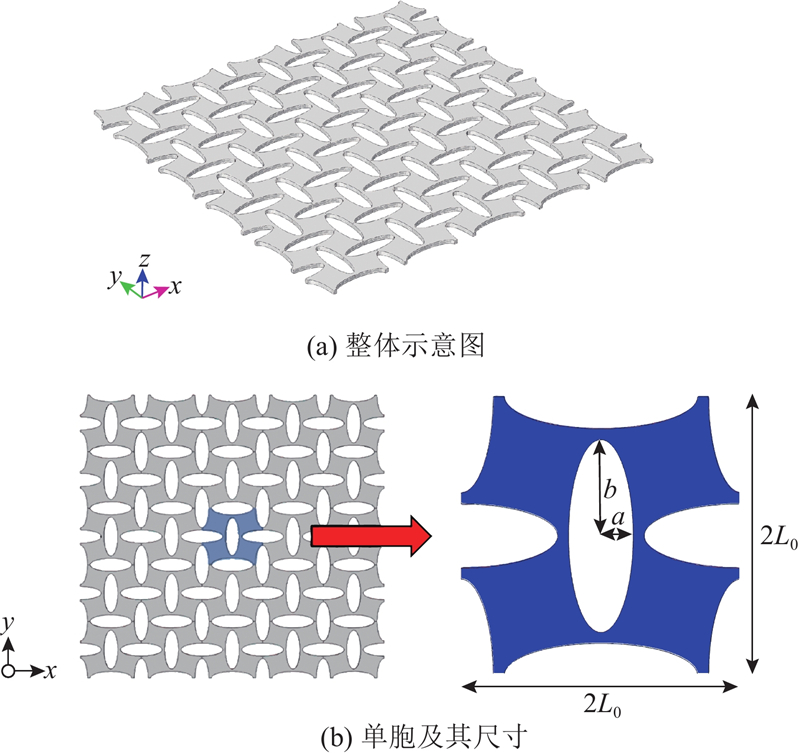
具有周期圆孔排列的软材料受到压缩荷载作用后将发生屈曲变形，屈曲后的构型之一类似于十字排列的椭圆孔周期结构；由于原有结构对称性的破坏，导致带隙特征发生较大的改变[18]. 后屈曲模态的定向诱导有一定的难度，容易受到结构初始几何缺陷、加载精度等的影响. 基于倒向思维，选用十字排列椭圆孔薄板结构作为研究对象，考察带隙特征. 十字排列椭圆孔薄板的整体结构如图1（a）所示，单胞如图1（b）所示，呈正方晶格排列. 计算模拟和实验测试都采用同一尺寸模型：板的厚度h=5 mm，单胞边长 $2{L_0}=96$ mm，在沿x和y方向上的单胞周期数均为5个. 记椭圆孔水平方向半轴长为a，竖直方向半轴长为b，则结构的孔隙率 $\phi $和椭圆孔长短轴之比κ如下.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   十字排列椭圆孔薄板结构

Fig.1   Thin plate with criss-crossed elliptical holes


$\phi = ab{\text{π}} /L_0^2\begin{array}{*{20}{c}} , &{} \end{array}\kappa = b/a.$
(1)

1.1. 周期结构能带计算

由于薄板在长、宽2个方向的尺寸均比厚度大得多，在考虑面内变形时可以认为薄板处于平面应力状态，应力−应变关系[19]为

${\sigma _{xx}} = \frac{E}{{1 - {\mu^2}}}\left( {\frac{{\partial {u_x}}}{{\partial x}} + \mu \frac{{\partial {u_y}}}{{\partial y}}} \right) = \alpha \frac{{\partial {u_x}}}{{\partial x}} + \beta \frac{{\partial {u_y}}}{{\partial y}},$
(2)

${\sigma _{yy}} = \frac{E}{{1 - {\mu ^2}}}\left( {\frac{{\partial {u_y}}}{{\partial y}} + \mu \frac{{\partial {u_x}}}{{\partial x}}} \right) = \beta \frac{{\partial {u_x}}}{{\partial x}} + \alpha \frac{{\partial {u_y}}}{{\partial y}},$
(3)

${\sigma _{xy}} = G\left( {\frac{{\partial {u_x}}}{{\partial y}} + \frac{{\partial {u_y}}}{{\partial x}}} \right).$
(4)

式中： ${\sigma _{ij}}$ 为应力张量； ${u_x}$ 和 ${u_y}$ 对应于x和y方向的位移分量； $E$ 为材料的弹性模量； $G$ 为切变模量； $\mu $ 为泊松比； $\alpha $ 和 $\beta $ 为材料常数，其表达式容易从式（2）、（3）获得. 相应的动力学控制方程为

$\rho \frac{{{\partial ^2}{u_x}}}{{\partial {t^2}}} = \frac{{\partial {\sigma _{xx}}}}{{\partial x}} + \frac{{\partial {\sigma _{xy}}}}{{\partial y}},$
(5)

$\rho \frac{{{\partial ^2}{u_y}}}{{\partial {t^2}}} = \frac{{\partial {\sigma _{yx}}}}{{\partial x}} + \frac{{\partial {\sigma _{yy}}}}{{\partial y}}.$
(6)

式中： $\rho $ 为密度， $t$ 为时间. 当结构中孔洞（散射体）沿x和y方向呈周期排列时，式（2）~（6）中的系数 $\alpha $、 $\beta $、 $G$、 $\rho $ 均为位置矢量 ${\boldsymbol{r}} = [x, y]$ 的周期函数.

当利用有限元方法求解带隙时，可以针对如图1（b）所示的一个单胞进行分析[18]. 单胞有限元网格剖分后，离散形式的特征方程为

$({{K}} - {\omega ^2}{{M}}){{U}} = {\bf{0}}.$
(7)

式中：U为节点位移的振幅矢量， $\omega $ 为振动或者弹性波传播的角频率，K为等效刚度矩阵，M为等效质量矩阵.

根据周期结构中平面波传播的Bloch定理可知，波场可以表示为

$\psi ({{r}}) = {{\rm{exp}}\,[ {{\rm{i}} ({{k}} \cdot {{r}})}]}{\psi _{{k}}}({{r}}).$
(8)

式中： ${\psi _{{k}}}({{r}})$ 为空间上周期函数，在平面应力情况下， ${{\psi}} = {[{u_x}, {u_y}]^{\rm{T}}}$， ${{k}} = {[{k_x}, {k_y}]^{\rm{T}}}$ 为波数矢量. 由式（8）可知，单胞在周期边界处须满足：

${{U}}({{r}} + {{a}}) = {{\rm{exp} }\,[{{\rm{i}} ({{k}} \cdot {{a}})}]}{{U}}({{r}}).$
(9)

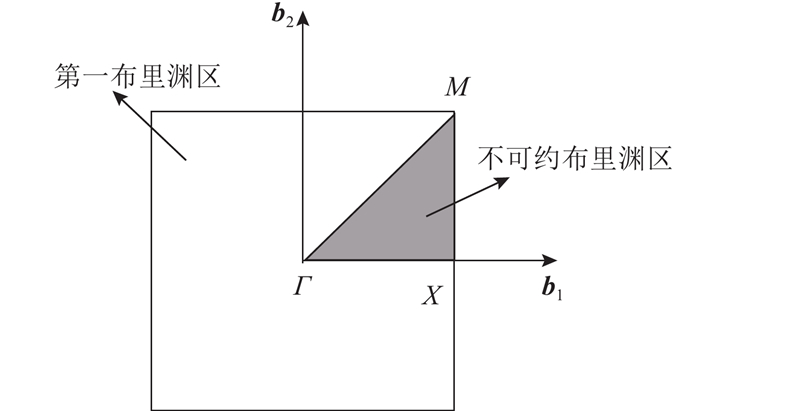
式中：a为晶格常数矢量. 联立式（7）、（9），可以在给定的波矢k下来求解特征频率；将频率反代入式（7），可以获得相对应的本征模态. 确定带隙位置时，只需将波矢k扫掠不可约Brillouin区边界，如图2所示. 图中，b1、b2为倒格子基矢量.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   正方晶格的第一布里渊区及不可约布里渊区

Fig.2   First Brillouin zone and irreducible Brillouin zone of squared lattice


使用商用有限元软件COMSOL Multiphysics 5.2a进行能带的有限元计算时，选择平面应力这一选项，和实验条件相对应；选择自由剖分的三角形网格，网格的大小满足收敛性要求；根据Bloch定理，在单胞的边界上施加Bloch条件. 相关材料参数如表1所示. 表中，ρ为密度，E为弹性模量.

表 1   试样材料参数

Tab.1  Mechanical properties of testing sample

材料 ρ/（g·cm−3） E/GPa μ
亚克力（PMMA） 1.18 2.7 0.4

新窗口打开| 下载CSV


当 $\phi = 50{{\text{%} }}$， $\kappa = 3.0$ 时，计算获得的二维十字排列椭圆孔薄板的能带结构，如图3所示. 图中，f为频率。可以发现，该声子晶体薄板在0~20 kHz频率下存在一条完全带隙（图中灰色部分），频率为8.01~15.10 kHz. 另外，在ΓX方向（对应空间上沿x方向）上有一条方向带隙（图中红色阴影部分），频率为7.55~15.20 kHz，稍宽于对应的完全带隙. 可见，基于倒向思维设计的十字排列椭圆孔薄板声子晶体在孔隙率较低时具有较宽的带隙.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

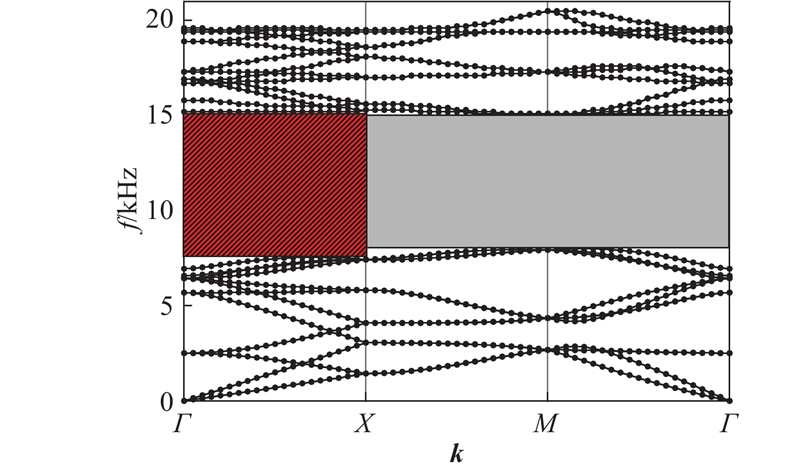
图 3   十字椭圆孔声子板的能带结构 $(\phi = 50{\text{%}}, \kappa = 3.0)$

Fig.3   Band structure of phononic plate with criss-crossed elliptical holes $(\phi = 50{\text{%}}, \kappa = 3.0)$


1.2. 有限尺寸传输特性的计算

为了与后续的实验结果进行对比，考察图1（a）所示的有限尺寸二维声子晶体薄板. 对应于能带图中ΓX方向的带隙作为测试目标，根据实验时实际激励及传感器接收的位置，在COMSOL中开展传输特性的有限元模拟. 整个声子晶体板采用自由边界，为了测试ΓX方向的传输特性，设定在一端边界中点施加沿x轴方向的单位位移激励，这相当于沿x方向对二维声子晶体薄板施加面内激励. 在另一端的中点处设置接收输出响应点，激励与接收响应的位置如图4所示.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   激励点与接收点位置示意图

Fig.4   Locations of incentive point and receiving point


将有限尺寸的传输谱计算结果与1.1节中针对无限尺寸声子晶体所获得的能带结构进行对比，如图5所示. 图中，T为传输率. 比较图5（a）、（b）可以发现，传输谱中衰减区域与ΓX方向带隙的位置和宽度吻合较好.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

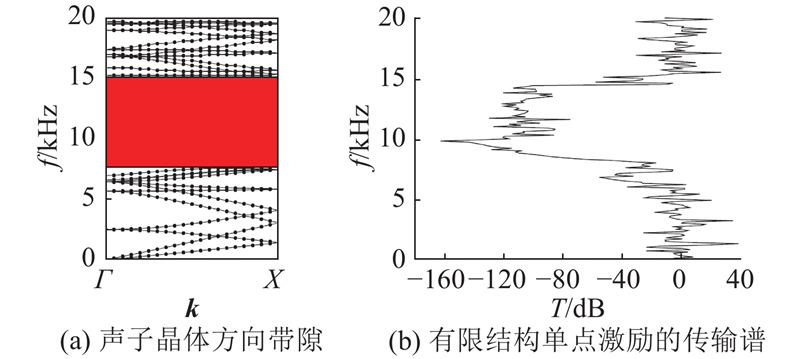
图 5   在ΓX方向上，声子晶体能带结构与传输谱对比

Fig.5   Comparison of band gap with transmission spectrum along ΓX direction


2. 实验研究

为了验证有限元仿真结果，设计相关的实验. 试样的几何尺寸和材料特性与有限元模型一致，试样采用激光切割加工，照片如图6所示.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   十字排列椭圆孔PMMA试样

Fig.6   PMMA sample with criss-crossed elliptical holes


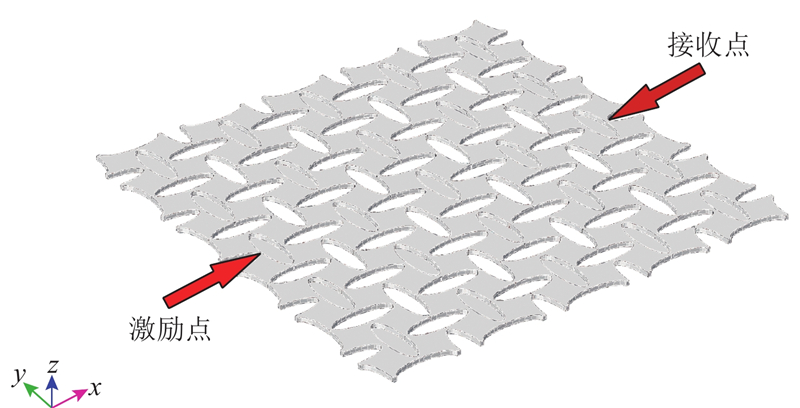
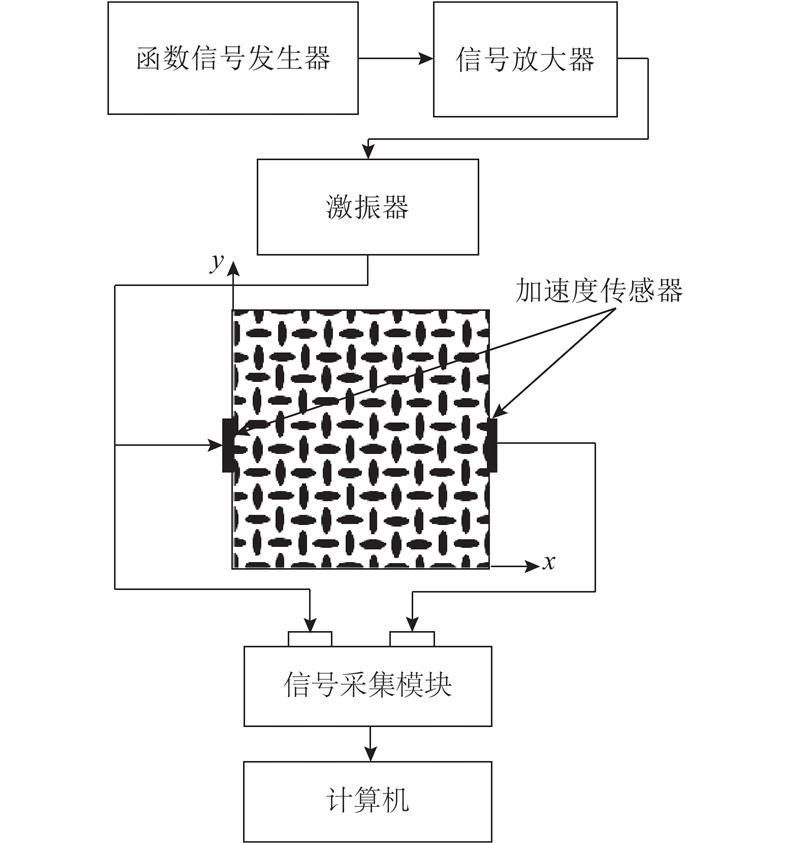
二维十字排列椭圆孔声子晶体带隙的实验测试系统及实景图分别如图7、8所示. 试样四角用吸盘固定在底座上，在其一端使用函数信号发生器及激振器（B&K公司4809型激振器），施加幅值为1 Vpp（Vpp为电压峰峰值）、沿x轴方向、频率为0~20 kHz的白噪声激励，这相当于沿着ΓX方向对二维声子晶体薄板结构进行纵向面内激励. 使用加速度传感器获得输入与输出信号，通过信号采集系统（B&K公司LAN-XI 3050型多功能输入模块）将模拟信号转换为数字信号，通过计算机完成数据的采集和分析（B&K公司的PULSE Labshop软件）. 在测试时，系统将瞬态透射时域信号进行快速傅里叶变换（FFT），获得信号的频谱. 通过对输入、输出信号的正则化处理，获得声子晶体ΓX方向的透射谱.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   波动测试系统示意图

Fig.7   Schema of wave propagation test system


图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   波动测试系统实景图

Fig.8   Wave propagation test setup


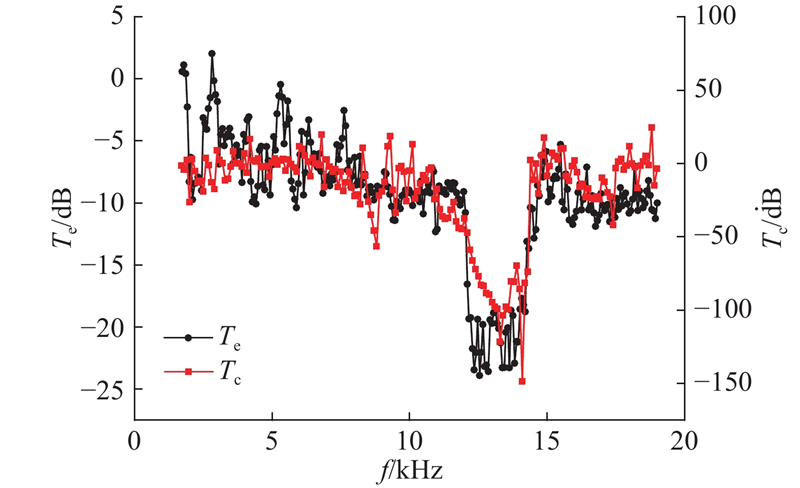
首先针对孔隙率为50%的呈正方晶格的圆孔声子晶体，开展实验测试，结果与仿真的对比如图9所示. 图中，Te、Tc分别为传输率的实验值和计算值. 可以看出，从透射谱中可以辨认出清晰的带隙，频率为12.2~14.8 kHz，这与有限元仿真结果吻合. 由于实验是输入电信号通过激振器给予试样以载荷激励，而有限元计算中采用了位移激励，两者传输谱的幅值不同.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   十字排列圆孔声子晶体ΓX方向透射谱实验与有限元结果对比 $(\phi = 50{\text{%}}, \;\kappa = 1.0)$

Fig.9   Transmission spectrum along ΓX direction by numerical method and experiment for phononic crystals with circular holes $(\phi = 50{\text{%}} ,\;\kappa = 1.0)$


3. 带隙特性的影响因素

3.1. 散射体（孔）几何参数对带隙特性的影响

对于十字排列椭圆孔结构，孔洞的几何参数对带隙特性会有显著的影响. 将孔隙率固定为ϕ=50%，改变孔洞的长短轴之比，通过有限元模拟及实验测试获得信号的频率响应特性曲线，如图10所示. 固定 $\kappa = 2$，改变ϕ，有限元模拟及实验测试结果的比较如图11所示.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   孔洞长短轴之比对ΓX方向带隙的影响

Fig.10   Effect of ratio of major axis to minor axis on band gap along ΓX direction


图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   结构孔隙率对ΓX方向带隙的影响

Fig.11   Effect of porosity on band gap along ΓX direction


对比图10、11所示的有限元仿真与实验结果可以看出，在相同孔隙率的情况下，孔洞的κ越大，带隙的起始频率越低，但带隙的终止频率几乎不变，导致带隙的宽度增大；在相同κ的情况下，ϕ越大，带隙的起始频率越低，带隙的终止频率几乎保持不变，因此带隙的宽度增大. 总之，对于十字排列椭圆孔声子晶体，ϕ越大，κ越大，越易在低频触发带隙，产生的带隙越宽. 与传统的圆孔声子晶体 $(\kappa = 1)$ 相比，十字排列椭圆孔结构 $(\kappa > 1)$ 更易产生较宽且处于低频的带隙.

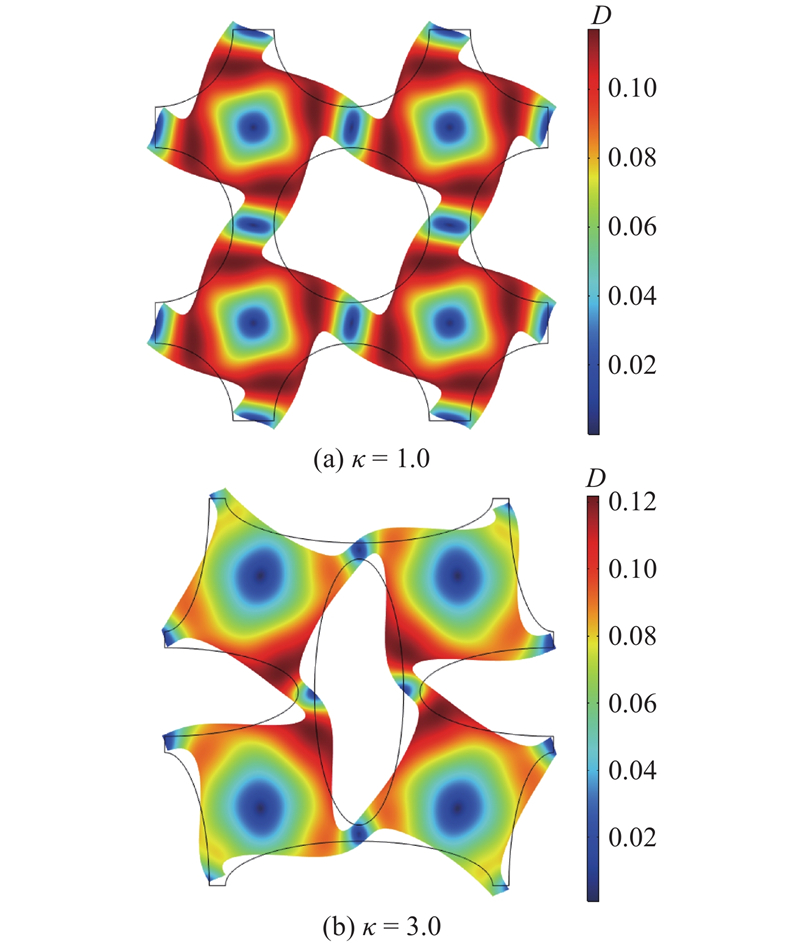
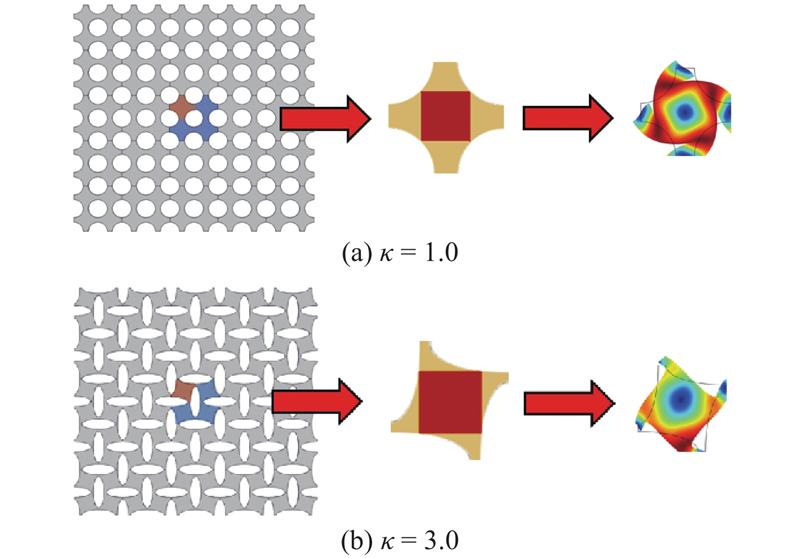
低频带隙的终止频率随着几何参数（长短轴之比、孔隙率）的变化甚微，触发带隙的起始频率会随着几何参数的变化而显著变化. 可见，孔几何参数对带隙的影响主要是对起始频率的影响. 在相同孔隙率的情况下，不同长短轴之比的十字交叉椭圆孔声子晶体在带隙的起始频率（下边界）处的波动模态如图12所示. 图中，D为波动位移. 分析带隙下边界处的模态图可以发现，可以将系统视作由质量块和不同粗细连接韧带组成的共振结构（见图13），波动模态可以看成是每个质量块绕其中心在板平面内的转动，转动频率与质量块的质量及连接韧带的刚度有关. 在相同孔隙率及相同单元尺寸的情况下，椭圆孔的长短轴之比越大，等效质量块的质量越大，连接韧带的刚度越小，从而导致共振频率和触发带隙的频率越低. 由于带隙上边缘频率基本保持不变，带隙的频率范围随着椭圆孔长短轴之比的增大而逐渐扩大.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   $\phi =50 {\text{%}}$ 时，不同长短轴之比带隙下边界的振动模态

Fig.12   Wave modes at lower edge of band gap with different ratios of major axis to minor axis when $\phi =50{\text{%}}$


图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   质量块-韧带等效结构示意图

Fig.13   Mass-ligament models


为了进一步观察二维十字排列椭圆孔声子晶体薄板带隙对波动传输特性的影响，图14给出带隙内、外2个频率点处薄板内波动位移分布. 图14（a）对应的频率点为5 kHz，位于带隙外，此时波动可以在薄板中传播，扰动分布在整个平面内；图14（b）对应的频率点为10 kHz，位于带隙内，此时在受激励点附近的波动幅度最大，在传播一定距离后会迅速衰减，导致弹性波无法在结构内传播.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   声子晶体薄板的波动位移分布

Fig.14   Contour plots of displacement for phononic crystal plate


3.2. 线缺陷对带隙的调控

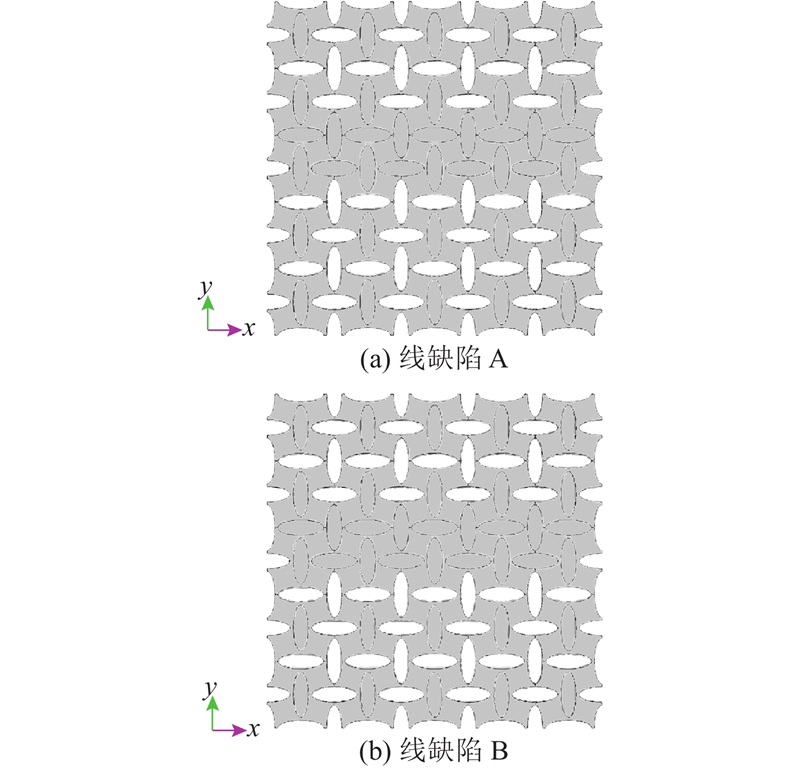
缺陷是指在理想周期结构声子晶体中引入对结构几何周期性的破坏，可以通过改变散射体的几何形状或尺寸、移走或添入散射体等方式来形成缺陷. 缺陷按照分布规律，可以分为点缺陷、线缺陷和面缺陷，它们的存在会对声子晶体的带隙特性产生重要的影响[20]. 研究在二维十字排列椭圆孔结构中，引入线缺陷来改变原有的带隙特性，从而实现对带隙的调控.

在ϕ=50%、κ=3.0的十字排列椭圆孔声子晶体薄板中，引入2种线缺陷，其中线缺陷A引入1排与基体同材料的夹杂，线缺陷B引入与基体同材料的2排夹杂，分别如图15（a）、（b）所示.

图 15

新窗口打开| 下载原图ZIP| 生成PPT

图 15   2种线缺陷

Fig.15   Two kinds of line defect


在对应实验中，通过在孔洞内插入与板相同厚度的PMMA椭圆柱来实现缺陷的引入. 分别对含A、B两种线缺陷的声子晶体薄板结构，开展传输谱的有限元计算及实验测量，结果如图16所示.

图 16

新窗口打开| 下载原图ZIP| 生成PPT

图 16   线缺陷对传输谱的影响

Fig.16   Effects of line defects on transmission


从图16可以看出，带隙的宽度随着引入缺陷的不同而发生变化，实验和计算结果吻合良好. 在未引入缺陷时，该结构在8~15 kHz下会发生明显的衰减，即产生较宽的带隙；当引入线缺陷A后，发生衰减的起始频率变大，发生衰减的频率范围减半，衰减强度变弱. 在未加缺陷的带隙范围内，例如10.1 kHz的频率下，引入缺陷A后，弹性波可以沿缺陷方向进行传播，如图17所示. 引入缺陷B后，原带隙特性几乎消失. 由此可见，线缺陷的引入破坏了结构原有的周期性，因而改变了原有的能带结构[17]. 在本例中，引入线缺陷A、B使得带隙宽度变窄，甚至使带隙消失，结果表明不同的线缺陷模式会导致不同的带隙调控结果. 通常利用软材料的大变形特性，通过机械加载实现对软材料声子晶体的带隙调控[21]. 对于硬材料多孔声子晶体，通过机械加载或偏场等方式对带隙的调控作用非常有限；通过添加夹杂引入线缺陷的方式，可以对带隙实现反向的大范围调控，为弹性波带隙的调控提供了一种新的方式. 只探索利用夹杂填充这一缺陷形式，以后将对其他缺陷形式作更多的研究比较，以期得到优化的调控方式.

图 17

新窗口打开| 下载原图ZIP| 生成PPT

图 17   10.1 kHz频率下，缺陷的引入对波传播的影响

Fig.17   Effects of defects on wave propagation under 10.1 kHz


4. 结　论

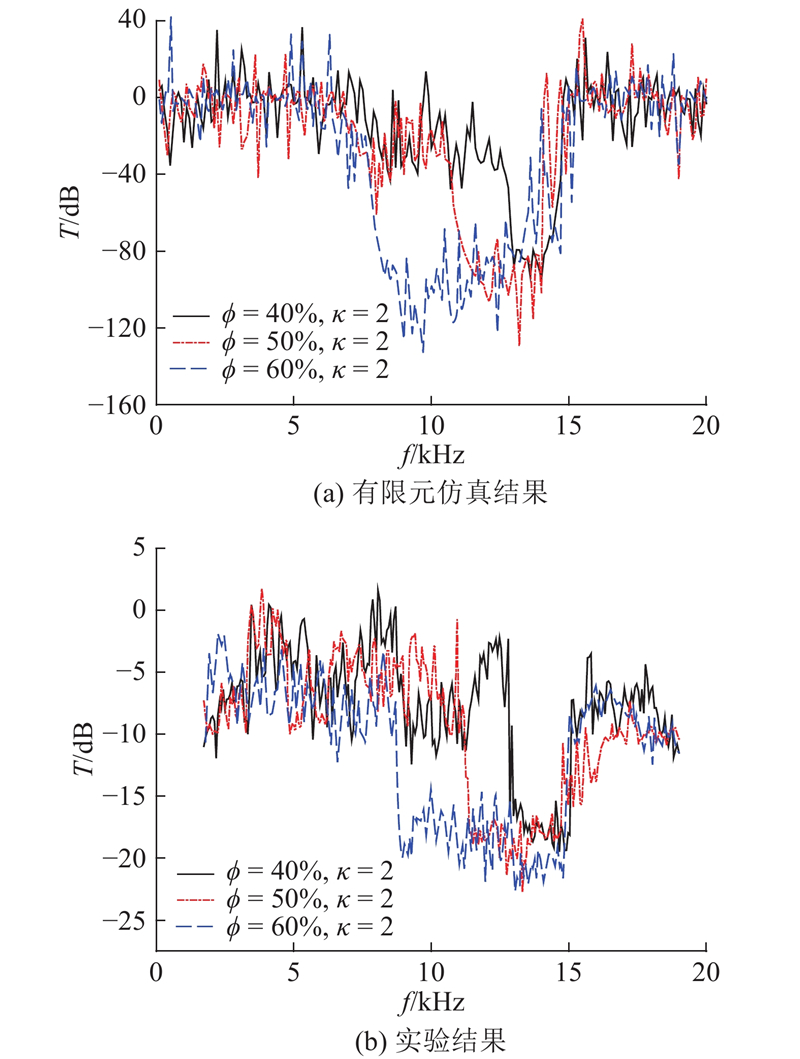
（1）对于二维十字排列椭圆孔声子晶体，ΓX方向带隙的宽度随着孔洞长短轴之比及孔隙率的增大而增大. 与传统研究的圆孔结构相比，二维十字排列椭圆孔结构可以获得更宽的低频带隙.

（2）带隙下边界的模态与共振单元的局域共振有关，在保持孔隙率和单元尺寸不变的情况下，随着椭圆孔长短轴半径比例的增加，该局域共振模态的频率不断降低，带隙上边界的位置基本保持不变，从而使得带隙的频率范围逐渐扩大.

（3）通过引入不同方式的线缺陷，可以改变结构中弹性波的传播特性，实现带隙的反向调控功能.

根据以上规律，改变二维十字排列椭圆孔声子晶体的几何参数及缺陷排布方式，能够设计出符合实际需要的声子晶体材料，为减振降噪的实际应用提供了重要的依据.

参考文献

SIGALAS M M, ECONOMOU E N

Elastic and acoustic wave band structure

[J]. Journal of Sound and Vibration, 1992, 158 (2): 377- 382

DOI:10.1016/0022-460X(92)90059-7      [本文引用: 2]

KUSHWAHA M S, HALEVI P, MARTÍNEZ G, et al

Theory of acoustic band structure of periodic elastic composites

[J]. Physical Review B, 1994, 49 (4): 2313- 2322

DOI:10.1103/PhysRevB.49.2313      [本文引用: 2]

MOHAMMADI S, EFTEKHAR A A, KHELIF A, et al

Complete phononic bandgaps and bandgap maps in two-dimensional silicon phononic crystal plates

[J]. Electronics Letters, 2007, 43 (16): 898- 899

DOI:10.1049/el:20071159      [本文引用: 1]

REINKE C M, SU M F, OLSSON R H, et al

Realization of optimal bandgaps in solid-solid, solid-air, and hybrid solid-air-solid phononic crystal slabs

[J]. Applied Physics Letters, 2011, 98 (6): 055405

[本文引用: 1]

WANG Y F, WANG Y S, SU X X

Large bandgaps of two-dimensional phononic crystals with cross-like holes

[J]. Journal of Applied Physics, 2011, 110 (11): 2059

[本文引用: 1]

DOWLING J P

Sonic band structure in fluids with periodic density variations

[J]. Journal of the Acoustical Society of America, 1992, 91 (5): 2539- 2543

DOI:10.1121/1.402990      [本文引用: 1]

SIGALAS M M, SOUKOULIS C M

Elastic-wave propagation through disordered and/or absorptive layered systems

[J]. Physical Review B, 1995, 51 (5): 2780

DOI:10.1103/PhysRevB.51.2780      [本文引用: 1]

AO X, CHAN C T

Complex band structures and effective medium descriptions of periodic acoustic composite systems

[J]. Physical Review B, 2009, 80 (23): 308- 310

[本文引用: 1]

LIU Z, CHAN C T, SHENG P, et al

Elastic wave scattering by periodic structures of spherical objects: theory and experiment

[J]. Physical Review B, 2000, 62 (4): 2446- 2457

DOI:10.1103/PhysRevB.62.2446      [本文引用: 1]

GARCIA-PABLOS D, SIGALAS M, FR M D E, et al

Theory and experiments on elastic band gaps

[J]. Physical Review Letters, 2000, 84 (19): 4349

DOI:10.1103/PhysRevLett.84.4349      [本文引用: 1]

SIGALAS M M, GARCÍA N

Theoretical study of three dimensional elastic band gaps with the finite-difference time-domain method

[J]. Journal of Applied Physics, 2000, 87 (6): 3122- 3125

DOI:10.1063/1.372308      [本文引用: 1]

MEAD D J

A general theory of harmonic wave propagation in linear periodic systems with multiple coupling

[J]. Journal of Sound and Vibration, 1973, 27 (2): 235- 260

DOI:10.1016/0022-460X(73)90064-3      [本文引用: 2]

LANGLET P, HLADKY‐HENNION A, DECARPIGNY J

Analysis of the propagation of plane acoustic waves in passive periodic materials using the finite element method

[J]. Journal of the Acoustical Society of America, 1995, 98 (5): 2792- 2800

DOI:10.1121/1.413244      [本文引用: 2]

黄屹澜, 高楠, 鲍荣浩, 等

周期结构后屈曲新算法及其应用

[J]. 计算力学学报, 2016, 33 (4): 509- 515

[本文引用: 1]

HUANG Yi-lan, GAO Nan, BAO Rong-hao, et al

A novel algorithm for post-buckling analysis of periodic structures and its application

[J]. Chinese Journal of Computational Mechanics, 2016, 33 (4): 509- 515

[本文引用: 1]

MARTÍNEZSALA R, SANCHO J, SÁNCHEZ J V, et al

Sound attenuation by sculpture

[J]. Nature, 1995, 378 (6554): 241

[本文引用: 1]

YANG C L, ZHAO S D, WANG Y S

Experimental evidence of large complete bandgaps in zig-zag lattice structures

[J]. Ultrasonics, 2017, 74: 99- 105

DOI:10.1016/j.ultras.2016.10.004      [本文引用: 1]

李建宝. 声子晶体带隙调控的数值与实验研究[D]. 北京: 北京交通大学, 2011.

[本文引用: 2]

LI Jian-bao. Numerical and experimental investigation on band gap engineering of phononic crystals [D]. Beijing: Beijing Jiaotong University, 2011.

[本文引用: 2]

BERTOLDI K, BOYCE M C

Mechanically triggered transformations of phononic band gaps in periodic elastomeric structures

[J]. Physical Review B, 2008, 77 (5): 439- 446

[本文引用: 3]

LANDAU L D, LIFSHITZ E M. Theory of elasticity [M]. Berlin: Springer, 1959.

[本文引用: 1]

温熙森, 温激鸿, 郁殿龙, 等. 声子晶体[M]. 北京: 国防工业出版社, 2009.

[本文引用: 1]

HUANG Y L, GAO N, CHEN W Q, et al

Extension compression-controlled complete band gaps in 2D Chiral square-lattice-like structures

[J]. Acta Mechanica Solida Sinica, 2018, 31 (1): 51- 65

DOI:10.1007/s10338-018-0004-z      [本文引用: 1]

/

〈 〉