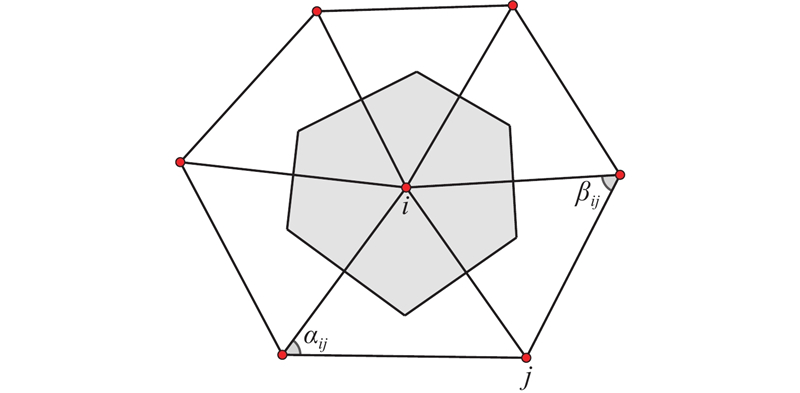
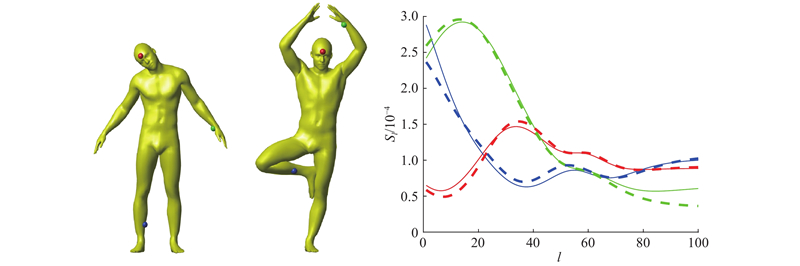
离散尺度的选取 离散小波尺度 ${t_j}$ ${L}$ ${\lambda _{\max }}$ J 确定. 最小和最大尺度分别为 ${t_J}{\rm{ = }}1/{\lambda _{\max }}$ ${t_1}{\rm{ = 2}}/{\lambda _{\min }}$ ${\lambda _{\min }} =$ $ {\lambda _{\max }}/u,$ $u > 0$ ${t_l}\;(l = 2, \cdots ,J - 1)$ $[{t_J},{t_1}]$ 图2 展示了位于模型同一点处的尺度函数和具有不同尺度的小波函数,其中J =7. 随着尺度 ${t_l}\;$ l 增大时),谱图小波在模型上的支撑域逐渐变小,这表示谱图小波具备自适应分析高频信息的能力. 事实上,当选定一组尺度 $\left\{ {{t_l}} \right\}_{l = 1}^J$ $F = \left\{ {{{\varphi }_i}} \right\}_{i = 1}^N$ $ \cup \left\{ {{{\psi }_{{t_l},i}}} \right\}_{l = 1,i = 1}^{J,N}$ $p = \mathop {\min }_{\lambda \in [0,{\lambda _{\max }}]} G(\lambda )$ $q = \mathop {\max }_{\lambda \in [0,{\lambda _{\max }}]} G(\lambda )$ $G(\lambda ){\rm{ = }}h{(\lambda )^2} + {\displaystyle\sum \nolimits _ {{l}}} {g{{({t_l}\lambda )}^2}} $ . 只有当p 和q 远离零时,才能保证信号f
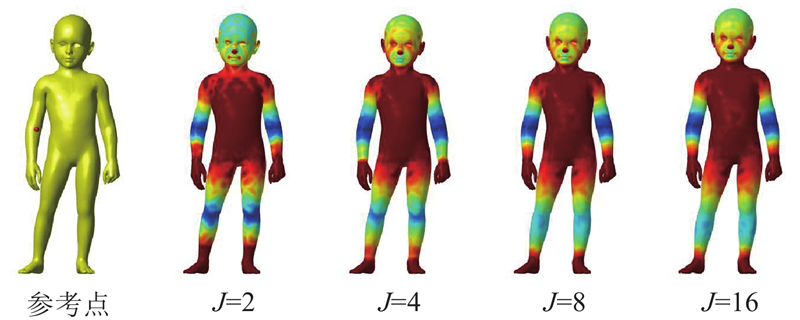
${\rm SGWD}(i) = \left( {{S_{{{\delta }_i}}}(i),{W_{{{\delta }_i}}}({t_1},i),{W_{{{\delta }_i}}}({t_2},i), \cdots ,{W_{{{\delta }_i}}}({t_J},i)} \right).$
[1]
BRONSTEIN A M, BRONSTEIN M M, OVSJANIKOV M. Feature-based methods in 3D shape analysis [M]//3D imaging, analysis and applications . London: Springer, 2012: 185–219.
[本文引用: 1]
[2]
SUN J, OVSJANIKOV M, GUIBAS L A concise and provably informative multi-scale signature based on heat diffusion
[J]. Computer Graphics Forum , 2010 , 28 (5 ): 1383 - 1392
[本文引用: 1]
[3]
AUBRY M, SCHLICKEWEI U, CREMERS D. The wave kernel signature: a quantum mechanical approach to shape analysis [C] // IEEE International Conference on Computer Vision Workshops . Barcelona: IEEE, 2011: 1626–1633.
[本文引用: 1]
[4]
BOSCAINI D, MASCI J, MELZI S, et al Learning class: specific descriptors for deformable shapes using localized spectral convolutional networks
[J]. Computer Graphics Forum , 2015 , 34 (5 ): 13 - 23
DOI:10.1111/cgf.2015.34.issue-5
[本文引用: 1]
[5]
SHUMAN D I, RICAUD B, VANDERGHEYNST P Vertex-frequency analysis on graphs
[J]. Applied and Computational Harmonic Analysis , 2016 , 40 (2 ): 260 - 291
DOI:10.1016/j.acha.2015.02.005
[本文引用: 1]
[6]
MELZI S, OVSJANIKOV M, ROFFO G, et al Discrete time evolution process descriptor for shape analysis and matching
[J]. ACM Transactions on Graphics (TOG) , 2018 , 37 (1 ): 4
[本文引用: 1]
[7]
LITMAN R, BRONSTEIN A M Learning spectral descriptors for deformable shape correspondence
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2014 , 36 (1 ): 171
DOI:10.1109/TPAMI.2013.148
[本文引用: 1]
[8]
BOSCAINI D, MASCI J, RODOLÀ E, et al Anisotropic diffusion descriptors
[J]. Computer Graphics Forum , 2016 , 35 (2 ): 431 - 441
DOI:10.1111/cgf.12844
[本文引用: 1]
[9]
HAMMOND D K, VANDERGHEYNST P, GRIBONVAL R Wavelets on graphs via spectral graph theory
[J]. Applied and Computational Harmonic Analysis , 2011 , 30 (2 ): 129 - 150
DOI:10.1016/j.acha.2010.04.005
[本文引用: 4]
[10]
KIM W H, PACHAURI D, HATT C, et al. Wavelet based multi-scale shape features on arbitrary surfaces for cortical thickness discrimination [C] // Advances in Neural Information Processing Systems . Doha: Curran Associates Inc, 2012: 1241–1249.
[本文引用: 1]
[11]
KIM W H, CHUNG M K, SINGH V. Multi-resolution shape analysis via non-euclidean wavelets: applications to mesh segmentation and surface alignment problems [C] // Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Portland: IEEE, 2013: 2139–2146.
[12]
KIM W H, ADLURU N, CHUNG M K, et al. Multi-resolutional brain network filtering and analysis via wavelets on non-Euclidean space [C] // International Conference on Medical Image Computing and Computer-Assisted Intervention . Berlin: Springer, 2013: 643–651.
[13]
ZHONG M, QIN H Sparse approximation of 3D shapes via spectral graph wavelets
[J]. The Visual Computer , 2014 , 30 (6-8 ): 751 - 761
DOI:10.1007/s00371-014-0971-0
[14]
TAN M, QIU A Spectral Laplace-Beltrami wavelets with applications in medical images
[J]. IEEE Transactions on Medical Imaging , 2015 , 34 (5 ): 1005 - 1017
DOI:10.1109/TMI.2014.2363884
[15]
LI C, HAMZA A B A multiresolution descriptor for deformable 3D shape retrieval
[J]. The Visual Computer , 2013 , 29 (6-8 ): 513 - 524
DOI:10.1007/s00371-013-0815-3
[本文引用: 1]
[16]
MEYER M, DESBRUN M, SCHRÖDER P, et al. Discrete differential-geometry operators for triangulated 2-manifolds [M]//Visualization and mathematics III . Berlin: Springer, 2003: 35–57.
[本文引用: 1]
[18]
BOGO F, ROMERO J, LOPER M, et al. FAUST: dataset and evaluation for 3d mesh registration [C] // IEEE Conference on Computer Vision and Pattern Recognition . Columbus: IEEE, 2014: 3794–3801.
[本文引用: 1]
[19]
ROBINETTE K M, DAANEN H. The CAESAR project: a 3d surface anthropometry survey [C] // International Conference on 3-D Digital Imaging and Modeling . Ottawa: IEEE, 1999: 380–386.
[本文引用: 1]
1
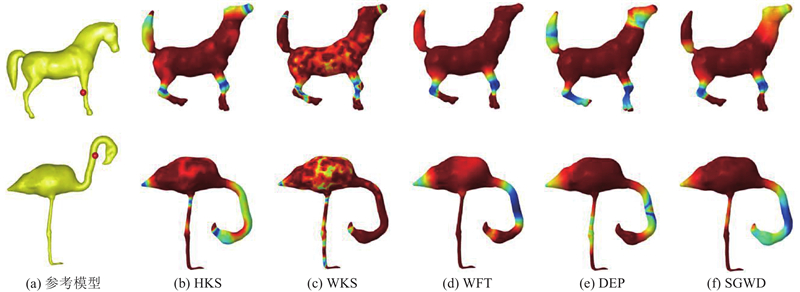
... 在实体动画、模型检索等有关三维形状分析和几何处理的许多应用中,模型匹配的准确性对算法起着至关重要的作用. 描述给定模型显著特征的主流方法之一是通过定义模型上各点的特征描述符,即编码该点邻域的多尺度形状信息和几何特征,实现模型整体几何特性的描述. 在众多建立点描述符的方法中,基于扩散几何的方法因具有许多显著的优点成为主流方法之一[1 ] . 其中建立点描述符的主要代表工作有热核签名(heat kernel signature,HKS)[2 ] 和波核签名(wave kernel signature,WKS)[3 ] . 从信号处理角度而言,这2种描述符具有统一的数学表达形式,均可以视为一组滤波器作用于拉普拉斯算子的特征值与特征向量. HKS源于一组低通滤波器的使用,主要分析模型的轮廓信息,因此无法实现模型之间点-点匹配时点的精确定位. WKS使用一组带通滤波器,能够获取模型更多的细节信息,实现了比HKS更准确的定位,但由于缺乏低通滤波器捕捉与模型轮廓相关的低频信息,匹配时容易产生大量的匹配噪声. Boscaini等[4 ] 利用多个几何向量的流形窗口傅里叶变换(WFT)[5 ] 系数,建立多尺度的点描述符. Melzi等[6 ] 通过模拟穿过网格点对之间所有路径的离散时间演化序列,创建多尺度的离散时间演化过程描述符(DEP). 此外,现阶段有许多工作根据不同的应用,利用机器学习建立三维模型点描述符[7 -8 ] . ...
A concise and provably informative multi-scale signature based on heat diffusion
1
2010
... 在实体动画、模型检索等有关三维形状分析和几何处理的许多应用中,模型匹配的准确性对算法起着至关重要的作用. 描述给定模型显著特征的主流方法之一是通过定义模型上各点的特征描述符,即编码该点邻域的多尺度形状信息和几何特征,实现模型整体几何特性的描述. 在众多建立点描述符的方法中,基于扩散几何的方法因具有许多显著的优点成为主流方法之一[1 ] . 其中建立点描述符的主要代表工作有热核签名(heat kernel signature,HKS)[2 ] 和波核签名(wave kernel signature,WKS)[3 ] . 从信号处理角度而言,这2种描述符具有统一的数学表达形式,均可以视为一组滤波器作用于拉普拉斯算子的特征值与特征向量. HKS源于一组低通滤波器的使用,主要分析模型的轮廓信息,因此无法实现模型之间点-点匹配时点的精确定位. WKS使用一组带通滤波器,能够获取模型更多的细节信息,实现了比HKS更准确的定位,但由于缺乏低通滤波器捕捉与模型轮廓相关的低频信息,匹配时容易产生大量的匹配噪声. Boscaini等[4 ] 利用多个几何向量的流形窗口傅里叶变换(WFT)[5 ] 系数,建立多尺度的点描述符. Melzi等[6 ] 通过模拟穿过网格点对之间所有路径的离散时间演化序列,创建多尺度的离散时间演化过程描述符(DEP). 此外,现阶段有许多工作根据不同的应用,利用机器学习建立三维模型点描述符[7 -8 ] . ...
1
... 在实体动画、模型检索等有关三维形状分析和几何处理的许多应用中,模型匹配的准确性对算法起着至关重要的作用. 描述给定模型显著特征的主流方法之一是通过定义模型上各点的特征描述符,即编码该点邻域的多尺度形状信息和几何特征,实现模型整体几何特性的描述. 在众多建立点描述符的方法中,基于扩散几何的方法因具有许多显著的优点成为主流方法之一[1 ] . 其中建立点描述符的主要代表工作有热核签名(heat kernel signature,HKS)[2 ] 和波核签名(wave kernel signature,WKS)[3 ] . 从信号处理角度而言,这2种描述符具有统一的数学表达形式,均可以视为一组滤波器作用于拉普拉斯算子的特征值与特征向量. HKS源于一组低通滤波器的使用,主要分析模型的轮廓信息,因此无法实现模型之间点-点匹配时点的精确定位. WKS使用一组带通滤波器,能够获取模型更多的细节信息,实现了比HKS更准确的定位,但由于缺乏低通滤波器捕捉与模型轮廓相关的低频信息,匹配时容易产生大量的匹配噪声. Boscaini等[4 ] 利用多个几何向量的流形窗口傅里叶变换(WFT)[5 ] 系数,建立多尺度的点描述符. Melzi等[6 ] 通过模拟穿过网格点对之间所有路径的离散时间演化序列,创建多尺度的离散时间演化过程描述符(DEP). 此外,现阶段有许多工作根据不同的应用,利用机器学习建立三维模型点描述符[7 -8 ] . ...
Learning class: specific descriptors for deformable shapes using localized spectral convolutional networks
1
2015
... 在实体动画、模型检索等有关三维形状分析和几何处理的许多应用中,模型匹配的准确性对算法起着至关重要的作用. 描述给定模型显著特征的主流方法之一是通过定义模型上各点的特征描述符,即编码该点邻域的多尺度形状信息和几何特征,实现模型整体几何特性的描述. 在众多建立点描述符的方法中,基于扩散几何的方法因具有许多显著的优点成为主流方法之一[1 ] . 其中建立点描述符的主要代表工作有热核签名(heat kernel signature,HKS)[2 ] 和波核签名(wave kernel signature,WKS)[3 ] . 从信号处理角度而言,这2种描述符具有统一的数学表达形式,均可以视为一组滤波器作用于拉普拉斯算子的特征值与特征向量. HKS源于一组低通滤波器的使用,主要分析模型的轮廓信息,因此无法实现模型之间点-点匹配时点的精确定位. WKS使用一组带通滤波器,能够获取模型更多的细节信息,实现了比HKS更准确的定位,但由于缺乏低通滤波器捕捉与模型轮廓相关的低频信息,匹配时容易产生大量的匹配噪声. Boscaini等[4 ] 利用多个几何向量的流形窗口傅里叶变换(WFT)[5 ] 系数,建立多尺度的点描述符. Melzi等[6 ] 通过模拟穿过网格点对之间所有路径的离散时间演化序列,创建多尺度的离散时间演化过程描述符(DEP). 此外,现阶段有许多工作根据不同的应用,利用机器学习建立三维模型点描述符[7 -8 ] . ...
Vertex-frequency analysis on graphs
1
2016
... 在实体动画、模型检索等有关三维形状分析和几何处理的许多应用中,模型匹配的准确性对算法起着至关重要的作用. 描述给定模型显著特征的主流方法之一是通过定义模型上各点的特征描述符,即编码该点邻域的多尺度形状信息和几何特征,实现模型整体几何特性的描述. 在众多建立点描述符的方法中,基于扩散几何的方法因具有许多显著的优点成为主流方法之一[1 ] . 其中建立点描述符的主要代表工作有热核签名(heat kernel signature,HKS)[2 ] 和波核签名(wave kernel signature,WKS)[3 ] . 从信号处理角度而言,这2种描述符具有统一的数学表达形式,均可以视为一组滤波器作用于拉普拉斯算子的特征值与特征向量. HKS源于一组低通滤波器的使用,主要分析模型的轮廓信息,因此无法实现模型之间点-点匹配时点的精确定位. WKS使用一组带通滤波器,能够获取模型更多的细节信息,实现了比HKS更准确的定位,但由于缺乏低通滤波器捕捉与模型轮廓相关的低频信息,匹配时容易产生大量的匹配噪声. Boscaini等[4 ] 利用多个几何向量的流形窗口傅里叶变换(WFT)[5 ] 系数,建立多尺度的点描述符. Melzi等[6 ] 通过模拟穿过网格点对之间所有路径的离散时间演化序列,创建多尺度的离散时间演化过程描述符(DEP). 此外,现阶段有许多工作根据不同的应用,利用机器学习建立三维模型点描述符[7 -8 ] . ...
Discrete time evolution process descriptor for shape analysis and matching
1
2018
... 在实体动画、模型检索等有关三维形状分析和几何处理的许多应用中,模型匹配的准确性对算法起着至关重要的作用. 描述给定模型显著特征的主流方法之一是通过定义模型上各点的特征描述符,即编码该点邻域的多尺度形状信息和几何特征,实现模型整体几何特性的描述. 在众多建立点描述符的方法中,基于扩散几何的方法因具有许多显著的优点成为主流方法之一[1 ] . 其中建立点描述符的主要代表工作有热核签名(heat kernel signature,HKS)[2 ] 和波核签名(wave kernel signature,WKS)[3 ] . 从信号处理角度而言,这2种描述符具有统一的数学表达形式,均可以视为一组滤波器作用于拉普拉斯算子的特征值与特征向量. HKS源于一组低通滤波器的使用,主要分析模型的轮廓信息,因此无法实现模型之间点-点匹配时点的精确定位. WKS使用一组带通滤波器,能够获取模型更多的细节信息,实现了比HKS更准确的定位,但由于缺乏低通滤波器捕捉与模型轮廓相关的低频信息,匹配时容易产生大量的匹配噪声. Boscaini等[4 ] 利用多个几何向量的流形窗口傅里叶变换(WFT)[5 ] 系数,建立多尺度的点描述符. Melzi等[6 ] 通过模拟穿过网格点对之间所有路径的离散时间演化序列,创建多尺度的离散时间演化过程描述符(DEP). 此外,现阶段有许多工作根据不同的应用,利用机器学习建立三维模型点描述符[7 -8 ] . ...
Learning spectral descriptors for deformable shape correspondence
1
2014
... 在实体动画、模型检索等有关三维形状分析和几何处理的许多应用中,模型匹配的准确性对算法起着至关重要的作用. 描述给定模型显著特征的主流方法之一是通过定义模型上各点的特征描述符,即编码该点邻域的多尺度形状信息和几何特征,实现模型整体几何特性的描述. 在众多建立点描述符的方法中,基于扩散几何的方法因具有许多显著的优点成为主流方法之一[1 ] . 其中建立点描述符的主要代表工作有热核签名(heat kernel signature,HKS)[2 ] 和波核签名(wave kernel signature,WKS)[3 ] . 从信号处理角度而言,这2种描述符具有统一的数学表达形式,均可以视为一组滤波器作用于拉普拉斯算子的特征值与特征向量. HKS源于一组低通滤波器的使用,主要分析模型的轮廓信息,因此无法实现模型之间点-点匹配时点的精确定位. WKS使用一组带通滤波器,能够获取模型更多的细节信息,实现了比HKS更准确的定位,但由于缺乏低通滤波器捕捉与模型轮廓相关的低频信息,匹配时容易产生大量的匹配噪声. Boscaini等[4 ] 利用多个几何向量的流形窗口傅里叶变换(WFT)[5 ] 系数,建立多尺度的点描述符. Melzi等[6 ] 通过模拟穿过网格点对之间所有路径的离散时间演化序列,创建多尺度的离散时间演化过程描述符(DEP). 此外,现阶段有许多工作根据不同的应用,利用机器学习建立三维模型点描述符[7 -8 ] . ...
Anisotropic diffusion descriptors
1
2016
... 在实体动画、模型检索等有关三维形状分析和几何处理的许多应用中,模型匹配的准确性对算法起着至关重要的作用. 描述给定模型显著特征的主流方法之一是通过定义模型上各点的特征描述符,即编码该点邻域的多尺度形状信息和几何特征,实现模型整体几何特性的描述. 在众多建立点描述符的方法中,基于扩散几何的方法因具有许多显著的优点成为主流方法之一[1 ] . 其中建立点描述符的主要代表工作有热核签名(heat kernel signature,HKS)[2 ] 和波核签名(wave kernel signature,WKS)[3 ] . 从信号处理角度而言,这2种描述符具有统一的数学表达形式,均可以视为一组滤波器作用于拉普拉斯算子的特征值与特征向量. HKS源于一组低通滤波器的使用,主要分析模型的轮廓信息,因此无法实现模型之间点-点匹配时点的精确定位. WKS使用一组带通滤波器,能够获取模型更多的细节信息,实现了比HKS更准确的定位,但由于缺乏低通滤波器捕捉与模型轮廓相关的低频信息,匹配时容易产生大量的匹配噪声. Boscaini等[4 ] 利用多个几何向量的流形窗口傅里叶变换(WFT)[5 ] 系数,建立多尺度的点描述符. Melzi等[6 ] 通过模拟穿过网格点对之间所有路径的离散时间演化序列,创建多尺度的离散时间演化过程描述符(DEP). 此外,现阶段有许多工作根据不同的应用,利用机器学习建立三维模型点描述符[7 -8 ] . ...
Wavelets on graphs via spectral graph theory
4
2011
... Hammond等[9 ] 类比于经典小波在频率域里的性质,基于谱图理论在图域上建立谱图小波变换(spectral graph wavelet transform,SGWT). 该小波继承了欧氏空间经典小波的许多性质,利用一组低通和高通滤波器实现图上信号的多频带分析. 该小波变换已广泛应用于多个三维模型处理领域,包括分片和校正、模型的稀疏表示和光滑、模型检索以及医学处理等[10 -15 ] . ...
... 经典小波由欧氏空间内的母小波函数伸缩平移获得,对于定义在三维曲面上的函数,没有直观自然的方式定义这些函数的伸缩和平移变换. 为了克服该问题,Hammond等[9 ] 类比经典小波在频率域里的滤波特性,基于谱图理论构建图域上的小波. 该小波具有很多与经典小波类似的性质,是分析图域空间信号的强有力工具. 为了充分利用三维模型的几何特征,利用拉普拉斯-贝尔特米算子的特征系统,基于谱图小波的框架构建更适合分析流形上信号的小波,称为谱图小波. ...
... 核函数的选取 在谱图小波工具箱(SGW_TOOLBOX)[9 ] 中提供了多种小波核函数,可以根据应用灵活的选择. 为了使各频率的影响相同,选取墨西哥帽小波核函数,在图4(c)中展示了具有不同尺度 ${t_l}$ $g(x) = x\exp\; ( - x)$
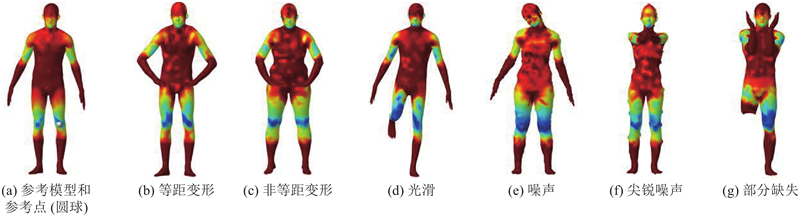
... 4)鲁棒性. 谱图小波理论[9 ] 保证了SGWD的鲁棒性. 图6显示了SGWD在经历了多种变形的模型上的鲁棒性. ...
1
... Hammond等[9 ] 类比于经典小波在频率域里的性质,基于谱图理论在图域上建立谱图小波变换(spectral graph wavelet transform,SGWT). 该小波继承了欧氏空间经典小波的许多性质,利用一组低通和高通滤波器实现图上信号的多频带分析. 该小波变换已广泛应用于多个三维模型处理领域,包括分片和校正、模型的稀疏表示和光滑、模型检索以及医学处理等[10 -15 ] . ...
Sparse approximation of 3D shapes via spectral graph wavelets
0
2014
Spectral Laplace-Beltrami wavelets with applications in medical images
0
2015
A multiresolution descriptor for deformable 3D shape retrieval
1
2013
... Hammond等[9 ] 类比于经典小波在频率域里的性质,基于谱图理论在图域上建立谱图小波变换(spectral graph wavelet transform,SGWT). 该小波继承了欧氏空间经典小波的许多性质,利用一组低通和高通滤波器实现图上信号的多频带分析. 该小波变换已广泛应用于多个三维模型处理领域,包括分片和校正、模型的稀疏表示和光滑、模型检索以及医学处理等[10 -15 ] . ...
1
... 采用最普遍的Meyer[16 ] 方法计算拉普拉斯-贝尔特米算子在三角网格X 上的离散形式,具体形式为 ...
Spectral mesh processing
1
2010
... 拉普拉斯矩阵L ${L}{{\phi }_k} =$ $ {\lambda _k}{{\phi }_k},\,\;k = 0,1, \cdots ,N - 1.$ ${{\phi }_k} = \left[{\phi _k}(i)\right] \in {\mathbb{{\bf{R}}}^N}$ . 事实上,L ${L^2}(X)$ [17 ] . 在实际计算中,求解L A −1 M ${M}{{\phi }_k} = \lambda {A}{{\phi }_k}$ . 由于L $\displaystyle\{ {\lambda _k}\} _{k = 0}^{N - 1}$ $0{\rm{ = }}{\lambda _0} < {\lambda _1} \leqslant \cdots \leqslant {\lambda _{N - 1}}$ . 对应的特征向量具有关于矩阵A
1
... 数据集 :实验采用FAUST[18 ] 和CAESAR[19 ] 这2个公共人体模型数据集,模型间点与点之间的准确对应已知. 这2个数据集中的模型因为存在非等距变形,且不同的对象间存在较大的差异,使得模型间点-点匹配非常具有挑战性. 其中FAUST包含10个不同的对象,且每个对象具有10个不同的姿势,共计100个模型,每个模型具有大约7 000个顶点. CAESAR 是最大的商业化人体模型数据集,包含超过4 500个对象且具有同一站立姿势的模型.选取fitted-mesh子数据集中的20个模型进行测试,每个模型大约具有6 000个顶点. ...
1
... 数据集 :实验采用FAUST[18 ] 和CAESAR[19 ] 这2个公共人体模型数据集,模型间点与点之间的准确对应已知. 这2个数据集中的模型因为存在非等距变形,且不同的对象间存在较大的差异,使得模型间点-点匹配非常具有挑战性. 其中FAUST包含10个不同的对象,且每个对象具有10个不同的姿势,共计100个模型,每个模型具有大约7 000个顶点. CAESAR 是最大的商业化人体模型数据集,包含超过4 500个对象且具有同一站立姿势的模型.选取fitted-mesh子数据集中的20个模型进行测试,每个模型大约具有6 000个顶点. ...