航空发动机叶轮超高周疲劳寿命预测方法

doi:10.3785/j.issn.1008-973X.2019.04.002

航空发动机叶轮超高周疲劳寿命预测方法

王延忠^,, 杨凯, 齐荣华, 陈燕燕, 李菲, 高浩

Ultra-high cycle fatigue life prediction method for aero engine impeller

WANG Yan-zhong^,, YANG Kai, QI Rong-hua, CHEN Yan-yan, LI Fei, GAO Hao

收稿日期: 2018-03-12

Received: 2018-03-12

作者简介 About authors

王延忠（1963—），男，教授，博导，从事抗疲劳制造研究.E-mail：yzwang63@126.com , E-mail：yzwang63@126.com

摘要

为了预测航空发动机叶轮的超高周疲劳寿命,以某型叶轮为研究对象，研究叶轮叶片在不同载荷状态下的应力和疲劳寿命. 建立叶轮的有限元模型，通过仿真分析叶轮叶片在离心、气动载荷作用下的应力变化情况；考虑叶轮叶片的表面状态，修正应力结果；基于位错偶极子模型及相关理论，建立TC4材料的超高周寿命预测模型；结合修正交变应力和寿命预测模型，实现了航空发动机叶轮的寿命预测. 对比分析现有模型和该模型下的寿命预测结果，结果表明：2种模型在低、高周范围内预测寿命的变化趋势一致；利用该模型有效解决了叶轮疲劳寿命的预测问题，预测值较贴近测试寿命；叶轮表面状态对疲劳寿命的预测结果影响较大，因为考虑了表面状态，寿命预测结果更贴近测试寿命值.

关键词： 航空发动机叶轮 ; 位错偶极子 ; 超高周疲劳 ; 寿命预测 ; 表面状态

Abstract

The stress and fatigue life of impeller of special equipment under different load conditions were analyzed in order to predict the ultra-high cycle fatigue life of aero-engine impellers. A finite element model of the impeller was established, and the stress changes of impeller blade which bears centrifugal and aerodynamic loads were simulated and analyzed. The results of further revise stress were achieved by considering surface state of impeller blade. An ultra-high cycle fatigue life prediction model for TC4 was established based on the dislocation dipole model and related theory. The service life for aero engine impeller was predicted by using the revised data and the prediction models. The service life predicted by existing model and the proposed model were compared. Results indicated that the changing of service life predicted by these two models showed the same trend in both low cycle and high cycle ranges. The problem of predicting the fatigue life of the impeller can be solved more effectively by the proposed model, and the predicted data was closer to the tested data. The surface state of the impeller had a greater impact on the prediction of fatigue life, because the predicted data was closer to the tested ones when considering the surface state.

Keywords： aero-engine impeller ; dislocation dipole ; ultra-high cycle fatigue ; life prediction ; surface state

PDF (1023KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王延忠, 杨凯, 齐荣华, 陈燕燕, 李菲, 高浩. 航空发动机叶轮超高周疲劳寿命预测方法. 浙江大学学报(工学版)[J], 2019, 53(4): 621-627 doi:10.3785/j.issn.1008-973X.2019.04.002

WANG Yan-zhong, YANG Kai, QI Rong-hua, CHEN Yan-yan, LI Fei, GAO Hao. Ultra-high cycle fatigue life prediction method for aero engine impeller. Journal of Zhejiang University(Engineering Science)[J], 2019, 53(4): 621-627 doi:10.3785/j.issn.1008-973X.2019.04.002

随着航空发动机性能的提升，发动机关键零部件的失效问题日益凸显. 作为航空发动机的关键传动件之一，叶轮的失效会对航空发动机造成非包容性破坏，引起灾难性后果^[1]. 开展航空发动机离心叶轮疲劳寿命预测方法研究具有重要的工程应用价值.

航空发动机压气机叶轮在工作时会承受离心载荷和高频气动载荷，实际的疲劳寿命会达到10⁸周次及以上^[2]. 该周次范围内的疲劳被称为超高周疲劳（very high cycle fatigue，VHCF，也称为ultra-high cycle fatigue或Gigacycle）^[3]. 由于实际工程的需求，材料的超高周疲劳性能受到广泛的关注，而且随着超声疲劳试验机的诞生，超高周疲劳研究得到广泛的开展^[4].

Neppiras^[5]研究黄铜和铝合金的超高周疲劳性能，首次绘制了10⁸周循环下的S-N曲线. Zhao等^[6]发现Ti-6Al-4V合金在空气和NaCl溶液中表现出的超高周特性不同，在NaCl溶液中会出现较低的疲劳极限. Xu等^[7]在研究AA2198-T8合金时发现，该合金在较低的应力幅值下疲劳寿命达到10⁹次，存在耐力疲劳极限，且此时的裂纹模式具有鱼眼特征. Xu等^[7-11]认为在超高周疲劳阶段，材料可能拥有第2个疲劳极限，但对第二疲劳极限表现形式的描述不一致. 这种现象可能是因材料受样件形状、载荷特征等因素影响导致的. 发展至今，超高周疲劳领域已经累积了大量的研究成果，但没有形成完善的超高周疲劳理论. 此外，在20 kHz的高频载荷作用下，材料的内摩擦会使样件温度急剧上升，因此在相关试验过程中，会通过压缩空气或液体对样件进行冷却，这与工程中零件的受载形式有一定的差异；相关超高周成果是否适用于工程实践，需要进一步的研究^[12].

在寿命模型方面，现有常用的寿命模型在多数情况下只能预测低、高周寿命^[13-15]. 部分模型^[16-17]结合材料的超高周疲特征劳和现有的理论基础，对现有模型进行修改，实现了超高周寿命的预测，但模型的适用性需要更多工程应用的检验. 零件的表面状态作为影响零件寿命的重要因素，在模型的使用过程中没有得到充分的体现，需要进一步的改进.

本文提出航空发动机叶轮超高周预测方法. 通过有限元方法，计算离心叶轮的交变应力；根据加工后的叶片表面状态对交变应力进行修正，获得修正交变应力；根据位错偶极子模型，提出针对TC4材料的超高周寿命预测模型；将修正交变应力代入模型，获得航空发动机叶轮的疲劳寿命. 对比分析不同情况下的疲劳寿命，发现使用该方法获得的寿命预测值与叶轮测试寿命较贴近.

1. 叶轮疲劳寿命预测及计算方法

叶轮疲劳寿命的预测流程如下：1）对叶轮进行静态结构分析，选择应力监测点，通过瞬态结构分析提取监测点应力变化数据；2）通过应力集中系数仿真模型，获取不同粗糙度对应的应力集中系数，根据应力集中系数和残余应力作用系数修正交变应力；3）使用雨流法处理修正交变应力，利用建立的寿命预测模型进行寿命预测.

1.1. 研究对象及工况简介

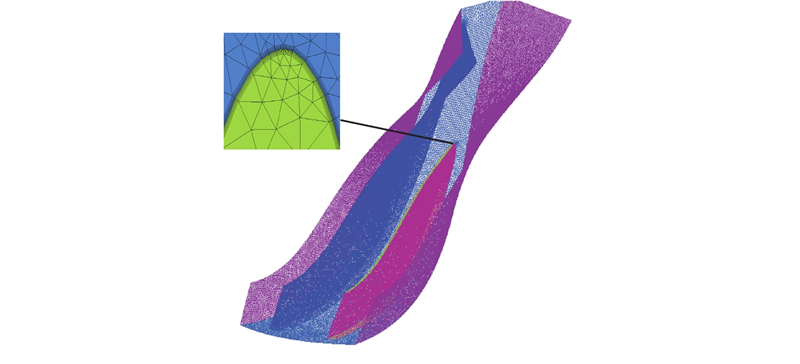
选取国内某型号涡轮轴发动机叶轮作为研究对象，如图1所示. 叶轮材料为TC4，主要的设计参数包括：设计转速为45 000 r/min，质量流量为3.25 kg/s，压比为1.9，叶片个数为11，分流叶片个数为11. 当叶轮进入工作状态，为发动机提供压缩空气时，转速保持45 000 r/min（设计转速）不变.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1 某型号离心叶轮

Fig.1 Certain type of centrifugal impeller

1.2. 交变应力的提取

经调研可知，该叶轮的疲劳失效部位为分流叶片前缘. 通过CFX15.0，求解作用在分流叶片上的气动载荷；通过ANSYS15.0，分析分流叶片在离心载荷、气动载荷作用下的应力状况.

1.2.1. 叶轮疲劳寿命计算模型及网格划分

叶轮疲劳寿命的计算模型如图2所示. 如图2（a）所示为气动载荷求解模型，通过单通道流场来模拟整圈流场，计算域包含大、小叶片各一个，叶轮后接等面积无叶片扩压器；如图2（b）所示为分流叶片模型.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2 叶轮疲劳寿命计算模型

Fig.2 Fatigue life calculation model for impeller

使用ICEM15.0软件完成叶轮及流道的非结构网格划分，流道与叶片在交界面上使用相同的网格节点. 为了满足湍流模型的计算要求，在机匣和叶片表面进行加密处理，如图3所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3 叶轮有限元模型

Fig.3 Finite element model of impeller

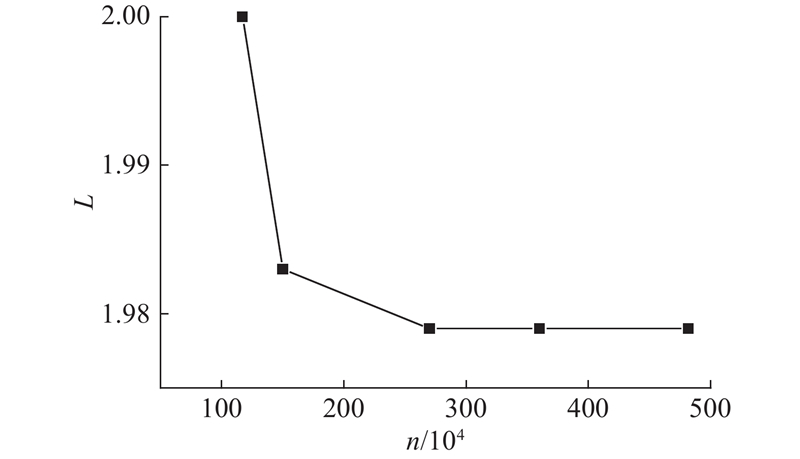
由于通道中存在复杂的激波反射和激波附面层干扰，在流体计算中，网格数量往往对数值模拟结果存在较大的影响. 为了保证数值模拟结果的可信度，对流道模型进行网格无关分析，如图4所示. 图中，n为网格数量，L为总压比. 从图4可见，出入口总压比在初始时随着网格数量的增加而减小，网格数量达到270万后，总压比不再变化，可以认为270万的网格数量能够满足数值计算的要求. 选取约270万的加密方案，对叶片流道进行加密.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4 总压比随网格数量变化图

Fig.4 Total pressure ratio curve with number of grids

1.2.2. 气动载荷求解设置

湍流模型选用 $k - \varepsilon $ 模型，进口湍流度为5%. 稳态计算时，平流项选择High Resolution，湍流模拟方法选择First Order. 瞬态计算时，空间上使用二阶迎风格式进行离散，时间上采用二阶向后Euler格式进行离散.

进口给定总压和总温，出口给定流量，具体参数参照叶轮的设计参数. 工作介质为理想气体. 固体壁面为绝热、光滑无滑移壁面，其中机匣表面绝对速度为0，其他壁面相对速度为0. 收敛判据为均方根残差<10⁻⁵，进、出口质量流量差<1%.

1.2.3. 静态结构分析设置和瞬态结构分析设置

通过ANSYS软件的静态结构分析模块，分析分流叶片在气动、离心载荷作用下的静态应力分布. 约束载荷情况如下：1）在叶片根部添加固定约束；2）对分流叶片施加45 000 r/min的惯性力；3）对分流叶片表面施加气动载荷，气动载荷由CFX稳态计算获取.

通过ANSYS软件的瞬态结构分析模块，分析分流叶片在气动离心载荷作用下的应力变化情况，计算时间为2.66×10⁻³s，计算360步. 约束载荷情况如下：1）在叶片根部添加固定约束；2）对分流叶片施加45 000 r/min的惯性力；3）每个分析步施加与之相对应的气动载荷，气动载荷由CFX瞬态计算获取.

1.3. 交变应力的修正

零件表面质量会显著影响零件的疲劳寿命，因此在寿命计算过程中考虑了残余应力、表面粗糙度以及显微硬度这3个对寿命有显著影响的表面特征量. 残余应力和表面粗糙度主要影响叶轮叶片的交变应力，显微硬度对交变应力的影响较小. 本文通过残余应力和表面粗糙度对交变应力进行修正，显微硬度会以参数的形式出现在寿命预测模型中.

表面粗糙度对疲劳应力的影响主要体现在应力集中上，残余应力对交变应力的影响主要体现在平均应力上^[18]，因此建立交变应力的修正公式如下：

(1) ${\delta _{\rm{R}}} = {K_{\rm{t}}}(\delta + m{\delta _{\rm{r}}}).$

式中：δ_R为修正后的交变应力，K_t为应力集中系数，δ为计算所得的交变应力，m为残余应力作用系数，δ_r为残余应力.

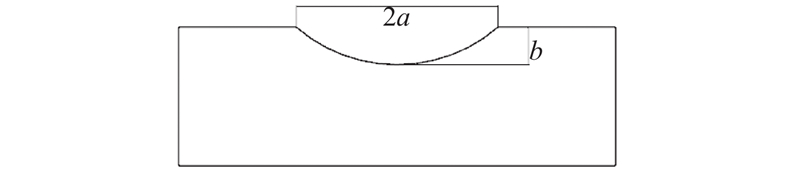
由式（1）可知，修正交变应力须确定残余应力作用系数m和应力集中系数K_t. 结合叶轮材料的热处理，选择残余应力作用系数为0.57^[19]. 为了求解应力集中系数，结合磨粒流加工特性，建立仿真模型如图5所示.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5 应力集中系数模型

Fig.5 Model of stress concentration coefficient

整体模型为一平板，平板的上缘有一圆弧缺口，平板两侧施加p=100 MPa的均布拉伸载荷. 图5中，2a为缺口宽度，b为缺口深度，R为磨粒的等效半径. 三者之间存在如下关系：

(2) ${a^2} + {(R - b)^2} = {R^2}.$

采用应力集中系数的计算公式如下：

(3) ${K_{\rm{t}}} = {\delta _{\max }}/{\delta _{\rm{n}}}.$

式中：K_t为应力集中系数，δ_max为最大Mises应力，δ_n为净截面名义应力.

1.4. 疲劳寿命的预测

根据Mura等^[20]提出的位错偶极子模型可知，假定发生超高周疲劳时，滑移带应力和摩擦应力存在如下关系：

(4) $f = \eta \delta.$

式中： $\delta $ 为垂直于剪切面的应力， $\eta $ 为摩擦因子，f为摩擦应力.

每单元厚度每次位错存储的应变能增能量 $\Delta U$ 可以表示为

(5) $\Delta U = \frac{{{\text{π}}(1 -\nu ){{(\Delta \tau - \eta \Delta \delta )}^2}{d^2}}}{{2 G }}.$

式中： $\nu $ 为泊松比； $\Delta \tau $（ $\Delta \delta $）为最大循环切应力（垂直应力）和最小循环切应力（垂直应力）之差；d为晶粒尺寸； $G$ 为切变模量， $G = E/[2\left( {1 + \nu } \right)]$，其中E为弹性模量.

当单位面积位错偶极子存储的应变能增量等于断裂能W_s时，空间偶记子的位错次数是裂纹萌生过程中裂纹的循环次数（疲劳寿命），能量等式如下：

(6) $2N{}_{\rm{i}}\Delta U = 4d{W_{\rm{s}}}.$

式中：N_i为裂纹循环次数.

联立式（5）、（6），可得

(7) ${N_{\rm{i}}} = \frac{{4G {W_{\rm{s}}}}}{{{\text{π}}(1 -\nu ){{(\Delta \tau - \eta \Delta \delta )}^2}d}}.$

根据裂纹萌生过程中能量的变化可知，萌生过程中裂纹萌生尺寸满足下式^[21-22]：

(8) $c = 0.002\;5{\left( {\frac{d}{h}} \right)^2}\frac{{{\gamma _{\rm{s}}}}}{G }.$

式中： $c$ 为裂纹长度， ${\gamma _{\rm{s}}}$ 为裂纹表面能，h为滑移带宽度.

当 ${\gamma _{\rm{s}}} = {W_{\rm{s}}}$ 时，联立式（7）、（8），可得

(9) $\left( {\Delta \tau - \eta \Delta \delta } \right)N_{\rm{i}}^{1/2} = {\left[ {\frac{{1\;600c{G^2}}}{{{\text{π}} d(1 - \nu )}}} \right]^{1/2}}\left(\frac{h}{d}\right).$

对于多晶体材料的疲劳裂纹萌生，载荷应力幅和滑移面的切应力幅满足如下关系：

(10) $\Delta \delta = M\Delta \tau. $

式中：M为晶粒最佳方向上测得的泰勒因子. 式（10）可以转化为

(11) $N_{\rm{i}}^{\rm{\alpha }} = \frac{1}{{k\Delta \delta }}{\left[ {\frac{{1\;600c{M^2}{G ^2}}}{{{\text{π}} d(1 - \nu )}}} \right]^{1/2}}\left(\frac{h}{d}\right).$

式中： $\alpha $ 为疲劳寿命指数，取决于位错塞积能及滑移的不可逆程度；k为应力转换系数；h为滑移带宽度； $\alpha $、k和h均由拟合得到.

参照Murakami等^[23]的疲劳极限理论，可以将裂纹萌生的应力幅作如下变换：

(12) $\Delta \delta = {{2{\delta _{\rm{a}}}}}/[((1-R_{\rm s})/2)\,^\beta]. $

式中： ${\delta _{\rm{a}}}$ 为应力幅值；R_s为应力比； $\beta $ 为修正系数， $\beta = 0.226 + {\rm HV} \times {10^{ - 4}}$，其中HV为维氏硬度.

联立式（11）、（12），可得疲劳寿命预测模型为

(13) $\begin{split} N_{\text{i}}^\alpha =& \left( {k{{\left[ {\left( {1 - R_{\rm s}} \right)/2} \right]}^\beta }/{\delta _{\text{a}}}} \right)\times\\&{\left[ {1\;600c{M^2}{G^2}/[d{{\pi }}(1 - \nu )]} \right]^{1/2}}\left( {h/d} \right). \end{split} $

将修正后的交变应力代入对应模型，可以获得相应的疲劳寿命.

2. 计算结果与讨论

2.1. 模型对比分析

该理论现有模型^[24]如下：

(14) $N_{\rm{i}}^{\rm{\alpha }} = \frac{1}{A}{\left[ {\frac{{1\;600c{M^2}{G^2}}}{{d{\text{π}} (1 -\nu )}}} \right]^{1/2}}\left(\frac{h}{d}\right).$

式中：A= $2{\delta _{\rm a}}/{\left[ {(1 - R_{\rm s})/2} \right]^\beta } - 2M_{\rm k}$，其中M_k为疲劳极限.

本文提出的模型如下：

(15) $N_{\text{i}}^\alpha = \frac{{k{{[\left( {1 - R_{\rm s}} \right)/2]}^\beta }}}{{{\delta _{\text{a}}}}}{\left[ {\frac{{1\;600c{M^2}{G^2}}}{{d{\text{π}}(1 - \nu)}}} \right]^{1/2}}\left( {\frac{h}{d}} \right).$

为了更直观地了解两模型的区别，对模型进行拟合，拟合数据如表1所示. 表中，N_f为疲劳寿命. 选取TC4参数为：M=2，E=111 GPa， $\nu $=0.34，d=10 mm，c=15.7 μm，HV=319 kgf/mm². 使用1stOpt软件，开展模型的拟合，拟合结果如表2所示.

表 1 TC4疲劳寿命数据^[24]

Tab.1 Fatigue life data of TC4

R_s	δ_a/MPa	M_k/MPa	N_f
−1	750	553	35 700
−1	725	553	135 600
−1	700	553	127 300
−1	675	553	168 950
−1	650	553	739 300
−1	625	553	2 173 600

新窗口打开| 下载CSV

表 2 疲劳寿命模型的参数拟合

Tab.2 Parameter fitting of fatigue life model

拟合参数	现有模型	本文模型
$\alpha $	0.255 1	0.035 4
h	0.021 3	—
kh	—	0.003 7

新窗口打开| 下载CSV

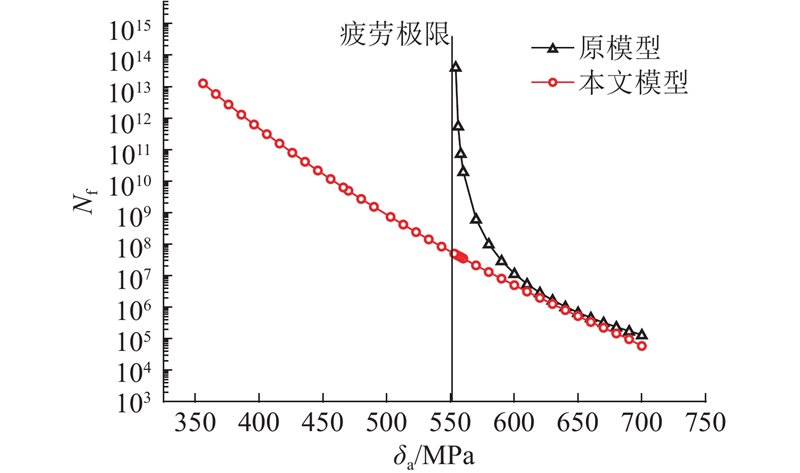
现有模型和本文模型的对比如图6所示. 可以看出，当R_s=−1时，存在如下情况：1）原模型虽然能够进行超高周寿命预测，但是当应力靠近疲劳极限值时，预测寿命趋于无穷，这和现有的超高周疲劳研究成果不一致，本文模型不存在该情况，理论上没有疲劳极限的限制；2）当交变应力低于疲劳极限时，原模型无法完成对疲劳寿命的预测，本文模型不存在该情况；3）在低、高周范围内，两模型的预测寿命随应力变化的趋势一致.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6 2种模型的疲劳寿命预测结果对比图

Fig.6 Comparison of fatigue life predicted by two models

引起现有模型和本文模型区别的原因是在模型推导过程中，两者采用了不同的摩擦应力的计算方法. 原模型认为在疲劳过程中摩擦应力为定值，在模型（14）中以疲劳极限相关量的形式体现. 当计算应力靠近疲劳极限时，预测寿命会惩罚性地贴近无穷，这不符合实际情况. 该模型无法对低于疲劳极限的应力进行寿命预测，难以满足实际需求. 本文模型假定在超高周范围内，摩擦应力和垂直于剪切面的应力成线性关系，使得模型（15）在计算贴近疲劳极限应力的寿命时，没有惩罚性操作，模型能够对低于疲劳极限的应力进行预测.

2.2. 叶轮受载分析

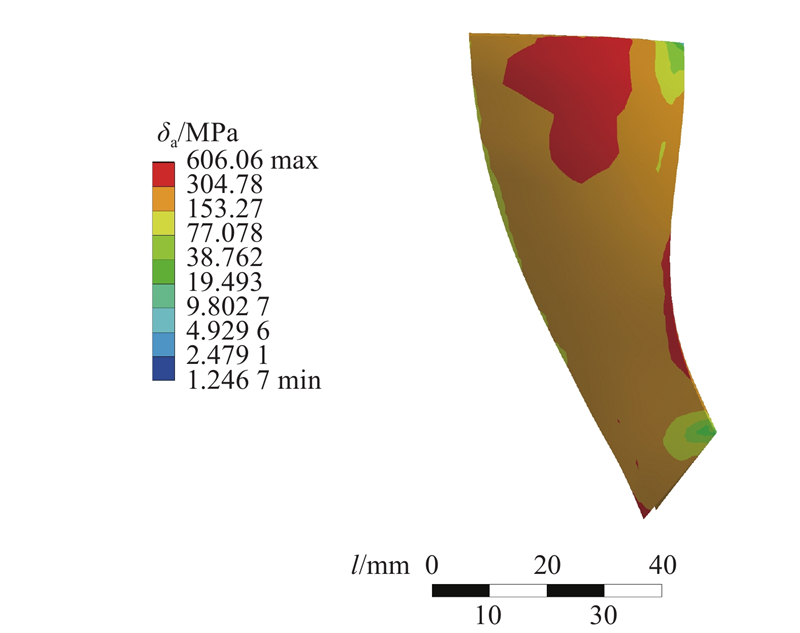
如图7所示为分流叶片静态结构分析的计算结果. 图中，l为叶片长度. 可以看出，此时分流叶片内应力较大的部位有2个，分别为叶片前缘和叶片外缘. 经了解可知，该叶轮在进行疲劳测试时，裂纹出现位置在分流叶片前缘中部附近，因此选取该区域内静态应力最大的点为最大应力监测点.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7 叶片静态分析应力结果

Fig.7 Static analysis stress result of blade

通过对分流叶片进行瞬态结构分析，获得应力监测点的主应力变化情况，如图8所示. 可以看出，应力监测点的第一主应力在数值上远远大于第二、三主应力，第一主应力的方向在叶片所在平面内. 选择第一主应力作为叶轮寿命预测的计算应力.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8 叶片瞬态分析结果

Fig.8 Transient analysis result of blade

2.3. 交变应力修正

该叶轮磨粒流工艺采用的磨粒为14目，因此R选为675 μm. 磨粒流表面粗糙度R_z和R_a的比值约为7^[25]，可以建立表面粗糙度R_a和b的相应关系. 如图9所示为不同表面粗糙度对应的应力集中系数. 可以看出，在一定范围内，应力集中系数随着粗糙度的增大呈现逐渐增大的趋势，应力集中系数变化不大，结合叶轮粗糙度检测结果，选取1.1作为叶轮应力集中系数.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

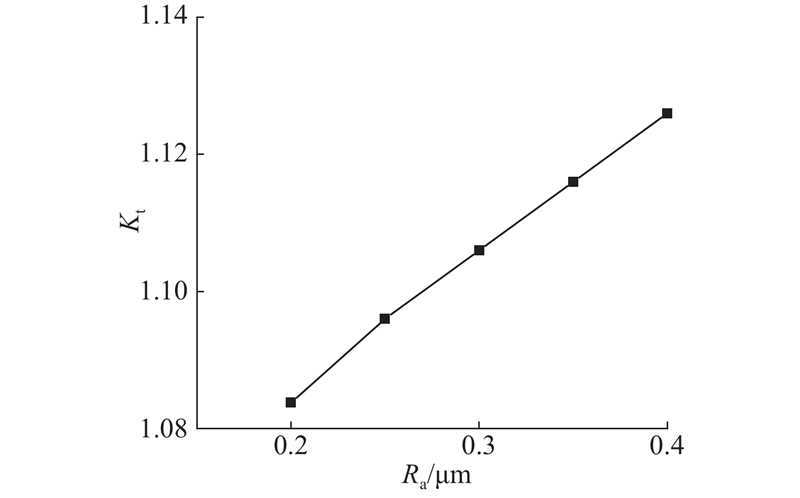
图 9 粗糙度和应力集中系数的关系曲线

Fig.9 Relationship between roughness and stress concentration coefficient

根据分流叶片残余应力检测结果，取−600 MPa作为本文的修正残余应力. 将应力集中系数、残余应力以及计算交变应力代入式（1），获得修正交变应力，如图10所示.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10 修正交变应力

Fig.10 Modified fatigue stress

2.4. 预测寿命分析

利用雨流法处理获得的应力数据，修正前交变应力的应力比约为0，应力幅值约为446 MPa；修正后交变应力的应力比约为−0.65，应力幅值约为490 MPa. 根据叶轮硬度检测结果，得到加工前、后零件的显微硬度分别约为320和379 kgf/mm². 将相应数值代入模型，得到相应的预测寿命，如表3所示.

表 3 寿命预测结果

Tab.3 Life prediction results

寿命预测前提条件	原模型	本文模型
不考虑表面质量	—	1.38×10⁸
考虑表面质量	—	3.59×10⁸

新窗口打开| 下载CSV

由于计算应力和修正应力幅值较小，在代入原模型时，式（14）第1项出现负值，无法获得寿命预测结果.

将计算应力代入本文模型，获得预测寿命为1.38×10⁸，等效寿命约为51 h. 将修正应力代入模型，获得预测寿命为3.59×10⁸，等效寿命约为132 h. 已知该叶轮通过台架试验获得的测试寿命约为200 h.

可以看出，通过该方法获得的预测寿命和叶轮测试寿命较贴近；表面状态对叶轮的寿命预测有较大的影响，考虑表面质量获得的预测寿命更接近叶轮的测试寿命.

3. 结　论

（1）建立航空发动机疲劳寿命预测模型，该模型在低、高周范围内与现有模型的预测寿命变化趋势一致，能够实现现有模型不能完成的超高周疲劳寿命预测.

（2）使用该模型计算某型号离心叶轮的疲劳寿命为3.59×10⁸，对应叶轮寿命约为132 h，和该叶轮实际测试得到的寿命较接近. 研究发现，叶轮的表面状态对寿命的预测影响很大，考虑表面完整性后得到的预测寿命会更接近叶轮的实际测试寿命.

（3）结合低频疲劳试验数据和现有的疲劳理论，对现有的疲劳模型进行修正. 将现有的低、高周疲劳成果向超高周疲劳领域进行拓展，为超高周疲劳寿命理论的丰富和工程化应用打下夯实的基础.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

毛鹏程. 离心压缩机叶轮断裂失效分析[D]. 大连: 大连理工大学, 2016: 2–8.