随着我国电网规模的不断扩大,尤其是长距离、高电压直流的电网建设,使得电力系统稳定性的分析和控制变得更加复杂,电网中低频振荡事件屡有发生,已成为危及电力系统安全运行及影响电网输送能力的关键问题[1-3]. 及时抑制低频振荡对整个电网安全稳定运行具有重要意义. 电力系统稳定器(power system stabilizer,PSS)因其物理概念清晰,模型结构简单,整定调试方便,已被公认为是抑制低频振荡最经济有效的方法. 传统的PSS能只针对特定振荡模态起作用,增加系统阻尼,提高系统稳定性,但是在多机系统(大区域电网)中则存在多个不同的振荡模态,且这些模态相互影响[4]. 采用传统方法设计的PSS可能在增大某一特定模态阻尼的同时会对另一个机电振荡模态起到反作用[5-7],恶化其他模态的阻尼,使整个系统的总阻尼变弱. 因此,在多机电力系统中独立设计性能优良的PSS并不一定总能保持良好的控制效果,只有对系统中所有PSS的参数进行统一协调和优化,才能使系统整体的控制效果达到最佳,提高系统总的阻尼比和鲁棒性[8-10]. 随着网架的不断扩大,区域间的振荡模式逐渐成为系统低频振荡的主导模式,使得基于广域信号的控制策略渐渐取代了只有本地信号的控制策略,这样最佳配置地点的选择和广域控制信号的选取就成为首要问题[11]. 总之,随着广域PSS的广泛应用,多个PSS之间的交互影响和协调成为当前研究的一个热点.
本文提出一种基于BA的多目标广域阻尼控制器协调设计方法. 运用BA中蝙蝠种群的多样性使得算法在迭代寻优过程中保持持续优化的能力,目标函数选取机电振荡模态的实部和阻尼比,将多机PSS参数优化问题归结为带不等式约束的多目标优化问题,并以多个运行方式验证此方法的鲁棒性.
1. 电力系统稳定器的数学模型
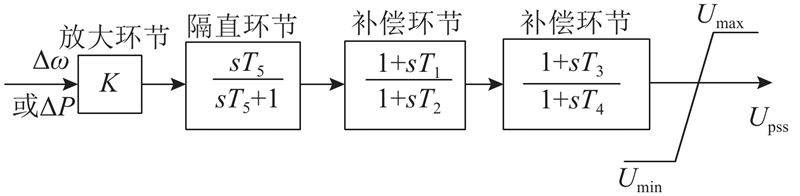
作为一种附加励磁控制技术,PSS在低频振荡抑制方面得到了广泛的应用,能够有效提高电力系统的动态稳定性,数学模型结构如图1所示. Δw为角速度增量,ΔP为功率增量,K、T1、T3为待优化的参数,其余的PSS参数均取经验值:T5=10 s,T2=T4=0.05 s. 该模型由放大环节、隔直环节、超前一滞后补偿环节以及限幅环节构成. 输出
图 1
图 1 常规电力系统稳定器(PSS)数学模型
Fig.1 Conventional power system stabilizer (PSS)mathematical model
2. 广域PSS协调控制目标分析
目标函数的选择直接决定着广域PSS设计的性能. 构造以阻尼比和特征值实部2个目标来改善系统阻尼及特征根分布,具体描述为
式中:
图 2
图 2
目标函数
Fig.2 Expected region of objective function J in complex plane
寻优的最终目的是保证在各种运行状况下
式中:i = 1,2,··· ,n;n为配置广域PSS的个数;
3. 蝙蝠算法的步骤及算法对比分析
3.1. 蝙蝠算法的步骤
(1)BA参数的初始化:给定蝙蝠种群的初始数量n,进化的代际数
(2)在解空间中对蝙蝠的位置
(3)进行算法终止条件的判断(是否满足搜索精度
(4)为了提高蝙蝠种群的多样性,引入周期函数来替代固定的系数值:
式中:Wave为引入的周期函数,
如果蝙蝠进入随机运动过程,则位置更新如下:
其中,
(5)计算蝙蝠的适应度并更新全局最优解;
(6)检查终止条件以决定返回(4)或终止程序以输出最佳结果.
3.2. 算法对比分析
分别采用蝙蝠算法和粒子群算法(particle swarm optimization,PSO)对2个测试函数(
每种智能算法均运行25次,并计算最优解的平均值如表1所示. 计算参数设值如下:BA的初始种群数目
表 1 蝙蝠算法(BA)与粒子群算法(PSO)的计算结果对比
Tab.1
| 测试函数 | PSO | BA | |||
| x* | t/s | x* | t/s | ||
| f (x,y) | 6.110 4×10−4 | 0.452 8 | 3.223×10−7 | 0.210 4 | |
| g (x,y) | 8.322 5×10−4 | 0.507 4 | 3.825×10−7 | 0.238 5 | |
4. 广域协调控制策略流程
(1)设置BA的相关初始化参数,确定多目标的优化值,并制定BA的终止准则;
(2)对开环电力系统用辨识算法进行特征值分析,得到全部的机电振荡模式,并通过计算留数矩阵,选择最优广域控制回路;
(3)确定优化参数的个数及约束条件并进入BA迭代循环,随机产生蝙蝠的初始位置,计算当前最优解,然后对电网闭环振荡响应曲线采用较强抗噪性能的COV-TLS-ESPRIT算法进行辨识分析[15],采样间隔为0.01 s,得到当前的阻尼比和特征根实部,并计算目标函数,更新PSS参数. 在满足终止准则条件下,使得目标函数达到最小值;
(4)在变异机制的作用下,蝙蝠跳出当前最优位置,在周围继续寻找最优解,若无则返回该位置;若找到最优解,则对最优解进行更新;
(5)判断是否满足终止条件,若不满足,则返回(3);若满足,则输出最优解(PSS参数),并在(2)中得到的最优控制回路中设置这些最优参数,使得整个系统实现广域协调控制. 基于多目标BA的广域协调控制流程图如图3所示.
图 3
图 3 多目标蝙蝠算法(BA)的广域协调控制流程图
Fig.3 Wide-area coordinated control flow chart of multi-target BA
5. 算例分析
5.1. 四机两区域互联测试系统
1)运行方式Ⅰ:额定运行方式,区域1向区域2通过2条联络线输送有功功率;
2)运行方式Ⅱ:区域1和区域2的负荷水平均为1 350 MW;
3)运行方式Ⅲ:区域1和区域2的负荷水平分别为1 150和1 650 MW.
在运行方式Ⅰ下对发电机G1的励磁参考电压在1 s时刻施加持续时间为0.2 s、幅值为0.05的脉冲干扰,可得到未安装PSS时的开环振荡模式,如表2所示. 其中,
表 2 未安装PSS时的开环振荡模式(运行方式I)
Tab.2
| 振荡模式 | 特征值 | ζ / % | f / Hz | 主导机组 |
| 1 | −0.629 ± j7.368 | 0.084 | 1.173 | G1 |
| 2 | −0.605 ± j7.218 | 0.083 | 1.149 | G3 |
| 3 | 0.032 ± j3.995 | −0.012 | 0.636 | G2,G3 |
考虑到控制器间的协调配置及相互影响,选取以下2种控制器配置方案.
1)方案A:每次只单独优化一台PSS参数,并选择在G1、G2、G3处分别安装3台本地PSS,反馈信号均取自本地转速角速度信号,以提高本地振荡模式的阻尼比;
2)方案B:安装3台PSS进行广域协调控制. 前2台PSS分别安装在发电机G1和G3上,并分别以输出转速作为反馈信号对2个局部振荡模式进行抑制;第3台以G3的输出转速作为广域信息反馈给G2的PSS,形成一条广域控制回路.
表 3 采用BA优化后的PSS参数(方案A)
Tab.3
| 发电机 | K | T1/s | T2/s |
| G1 | 20.12 | 0.211 | 0.102 |
| G2 | 20.32 | 0.203 | 0.101 |
| G3 | 20.24 | 0.216 | 0.101 |
表 4 采用BA优化后的广域PSS参数(方案B)
Tab.4
| 发电机 | K | T1/s | T3/s |
| G1 | 17.504 | 0.914 | 0.266 |
| G3 | 19.382 | 0.117 | 0.819 |
| G2,G3(广域) | 11.935 | 0.819 | 0.142 |
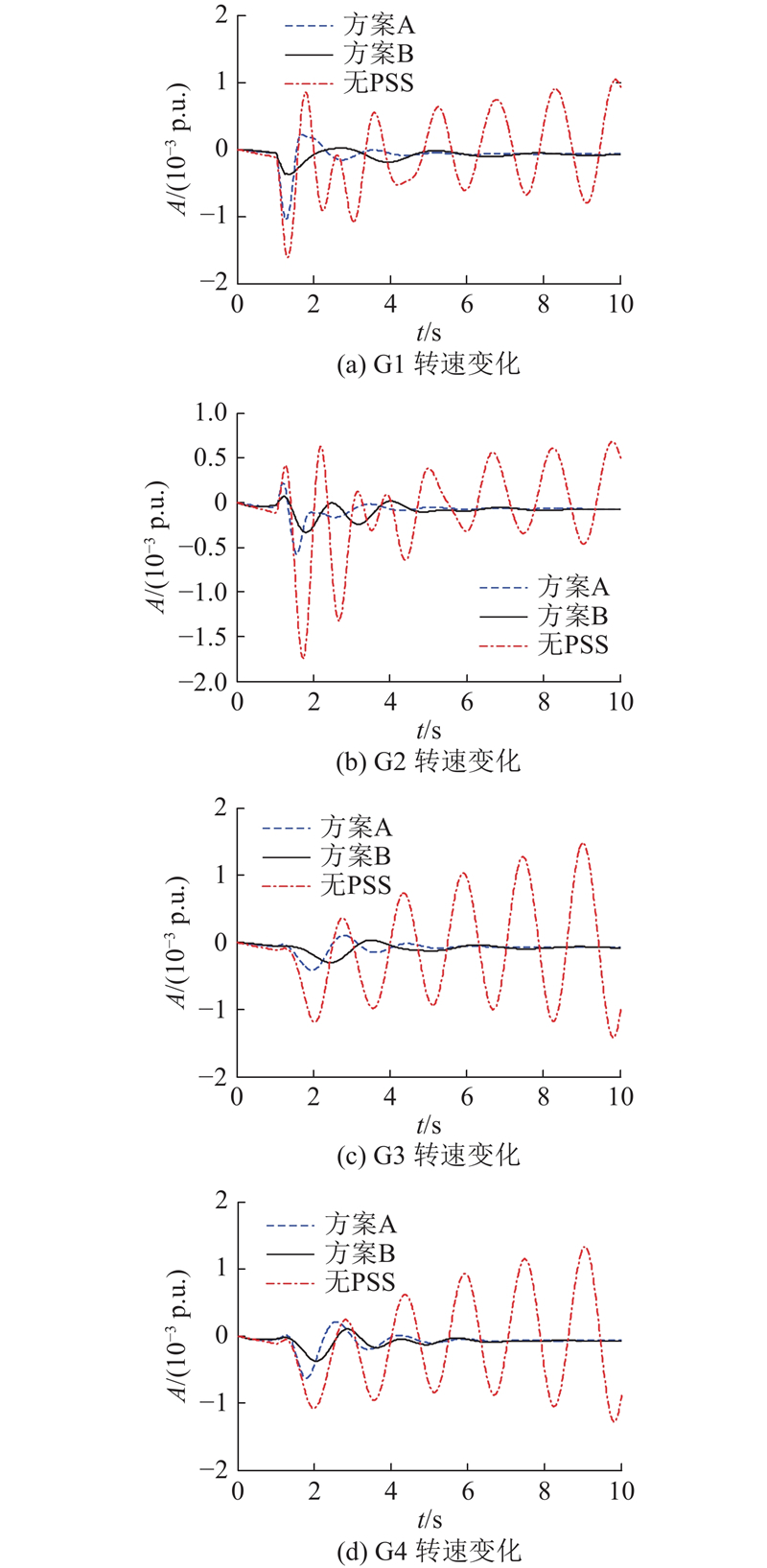
图 4
图 4 小干扰下发电机G1~G4的转速变化信号曲线
Fig.4 Signal curve for Speed change of generators G1 to G4 under disturbance
图 5
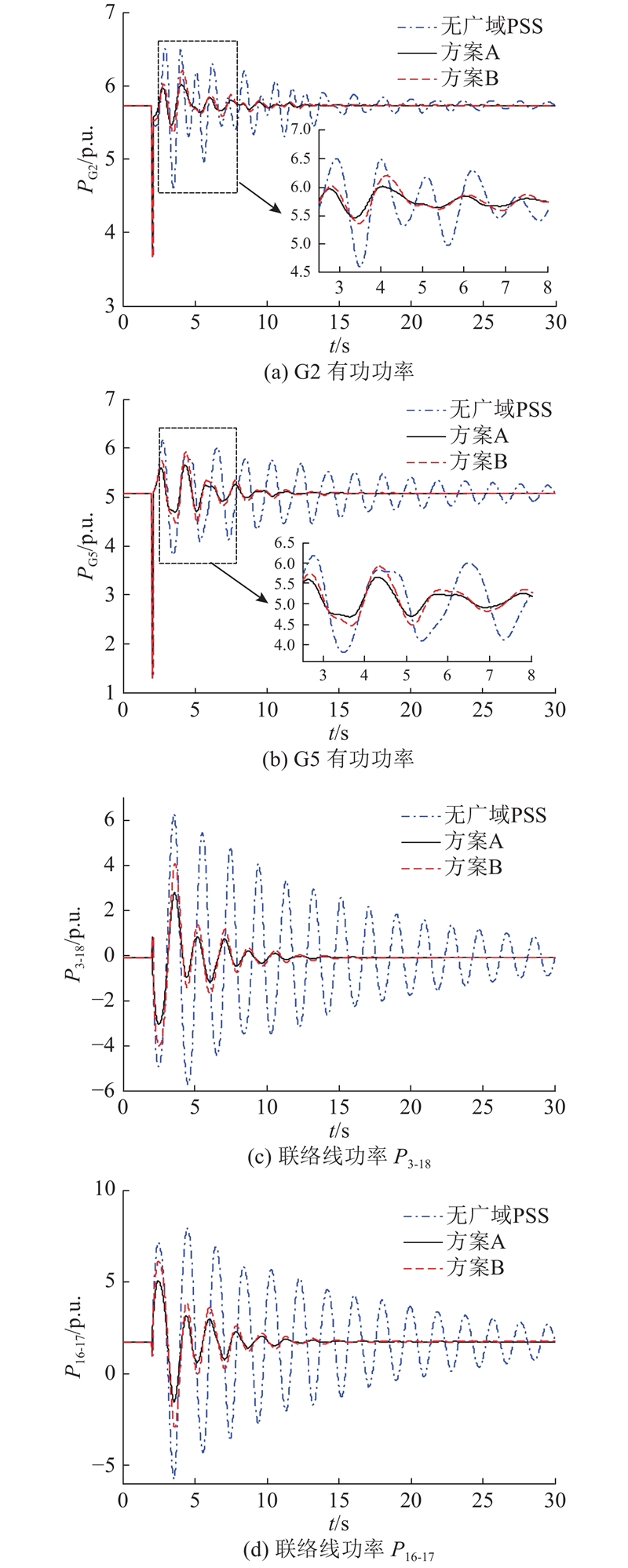
在未安装PSS的情况下,系统的振荡呈发散态势;在加装PSS后系统的振荡均得到了很好的抑制. 采用方案A对系统加装3台单独设计的本地PSS后,系统振荡的阻尼比得到有效的提高,但是对区域间振荡的抑制效果有限;采用方案B对系统加装广域协调设计的PSS后,区域间振荡得到了有效抑制,前两摆的超调量较方案A小.
图 6
图 6 短路故障下发电机G1~G4的转速变化信号曲线
Fig.6 Signal curve for speed change of generators G1 to G4 under short-circuit fault
图 7
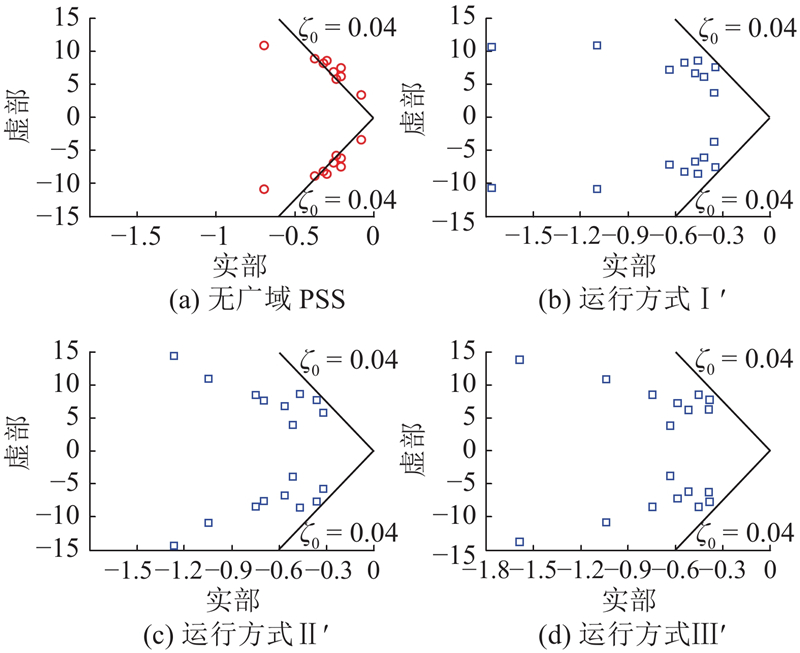
如图8所示为3种典型运行方式下无PSS时和按照方案B安装PSS时系统的机电模式特征值在复平面的分布图. 可以看出,在开环状态下(无PSS),3种典型的运行方式的机电模式均靠近虚轴,甚至已经进入右半平面,此时系统已不稳定或临界稳定;在闭环状态下(按照方案B安装PSS),3种典型运行方式的机电模式特征值已全部进入优化的目标区域,说明运用BA配置的方案B能够有效地将系统特征值移动到期望区域.
图 8
图 8 系统安装PSS前、后的机电模式特征值分布
Fig.8 Distribution of eigenvalues with or without PSS
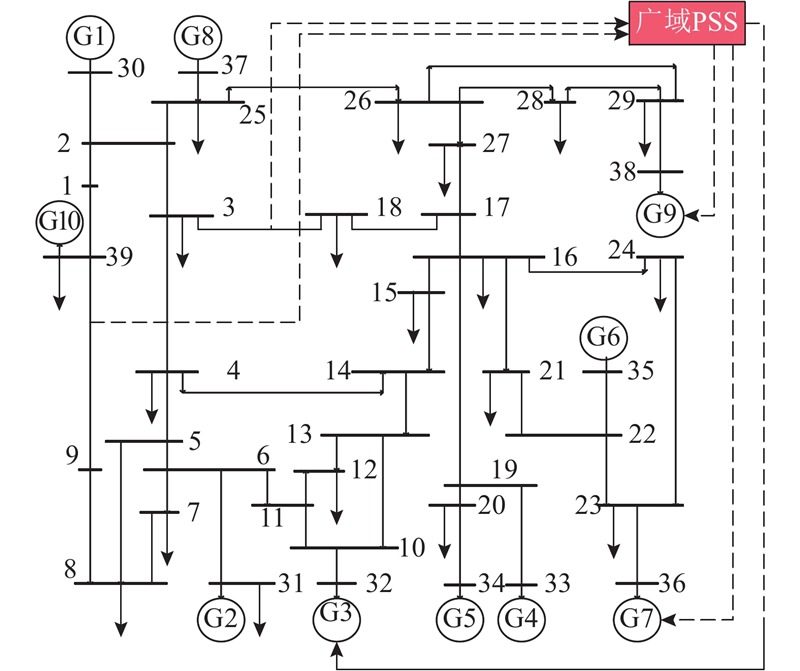
5.2. 新英格兰典型系统
图 9
表 5 未加入PSS时新英格兰系统的机电模式特征值
Tab.5
| 振荡模式 | 运行方式Ⅰ′ | 运行方式Ⅱ′ | 运行方式Ⅲ′ | |||||
| 特征值 | ζ/% | 特征值 | ζ/% | 特征值 | ζ/% | |||
| 1 | −0.077 2 ± j3.404 9 | 2.266 9 | −0.072 4 ± j3.285 2 | 2.204 0 | −0.021 3 ± j3.080 2 | 0.690 9 | ||
| 2 | −0.237 1 ± j5.779 3 | 4.098 5 | −0.201 5 ± j5.595 7 | 3.598 4 | −0.167 1 ± j5.542 6 | 3.012 8 | ||
| 3 | −0.209 1 ± j6.216 3 | 3.361 4 | −0.190 5 ± j5.903 8 | 3.224 6 | −0.260 6 ± j5.917 3 | 4.399 5 | ||
| 4 | −0.252 5 ± j6.855 4 | 3.680 8 | −0.285 1 ± j6.681 1 | 4.263 6 | −0.183 2 ± j6.225 4 | 2.941 6 | ||
| 5 | −0.208 6 ± j7.476 6 | 2.788 8 | −0.197 1 ± j7.455 1 | 2.643 3 | −0.199 5 ± j7.484 5 | 2.665 0 | ||
| 6 | −0.319 9 ± j8.131 1 | 3.931 0 | −0.320 7 ± j8.129 2 | 3.941 4 | −0.313 9 ± j8.017 6 | 3.912 7 | ||
| 7 | −0.297 2 ± j8.618 3 | 3.446 7 | −0.298 5 ± j8.596 5 | 3.470 7 | −0.289 4 ± j8.487 2 | 3.407 3 | ||
| 8 | −0.372 0 ± j8.841 2 | 4.203 8 | −0.372 5 ± j8.841 1 | 4.209 1 | −0.347 9 ± j8.779 1 | 3.959 4 | ||
| 9 | −0.694 5 ± j10.855 5 | 6.384 6 | −0.694 3 ± j10.851 2 | 6.385 2 | −0.690 1 ± j10.811 7 | 6.370 0 | ||
表 6 新英格兰系统模态分析结果
Tab.6
| 振荡模式 | 类型 | f/Hz | 参与机组 |
| 1 | 区间 | 0.542 | (G10)vs(G1,G2,G3,G4, G5,G6,G7,G8,G9) |
| 2 | 区间 | 0.912 | (G4,G5,G6,G7)vs(G2,G3), (G1,G8,G9) |
| 3 | 区间 | 0.988 | (G2,G3) vs (G1,G8,G9) |
| 4 | 本地 | 1.091 | (G4) vs (G5,G6,G7) |
| 5 | 本地 | 1.190 | (G9) vs (G1,G8) |
| 6 | 本地 | 1.294 | (G2) vs (G3) |
| 7 | 本地 | 1.372 | (G4) vs (G5) |
| 8 | 本地 | 1.407 | (G6) vs (G7) |
| 9 | 本地 | 1.728 | (G1) vs (G8) |
表7给出了3个区间模式下最大可控性的PSS安装位置和最大可观性的广域输入信号. 其中
表 7 广域输入信号与PSS安装位置
Tab.7
| 模式 | PSS安装位置 (最大可控性) | 广域输入信号 (最大可观性) |
| 1 | G9 | |
| 2 | G7 | |
| 3 | G3 | |
采用以下2种控制方案。方案A:P9-39和P3-18共同作为广域PSS控制器的输入;方案B:P3-18作为广域PSS控制器的唯一输入。同时,方案A和B的输出均控制G3、G7、G9. 广域PSS控制器的输入、输出信号,如图9中虚线所示. 计算目标函数的期望区域,其中
表 8 BA优化后广域PSS参数(方案A)
Tab.8
| 发电机 | K | T1/s | T3/s |
| G3 | 14.975 | 0.391 | 0.253 |
| G7 | 13.203 | 0.530 | 0.363 |
| G9 | 20.323 | 0.169 | 0.054 |
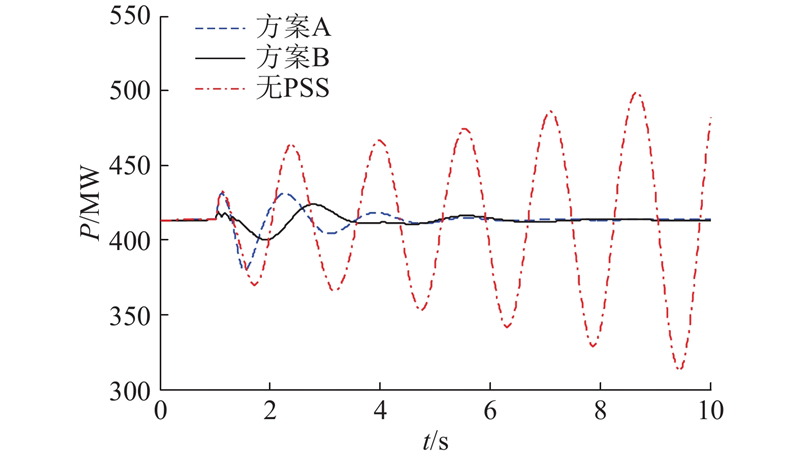
在运行方式Ⅰ′条件下,联络线17-18中段在2 s发生三相短路故障,2.06 s故障切除,采用2种控制方案优化设计的广域PSS与系统未加入广域PSS时的仿真结果对比如图10所示. 未安装广域PSS控制器时,系统发生低频振荡,且30 s后仍不能平息;运用BA设计的广域PSS进行协调控制后,方案A和方案B均能够有效抑制发电机和联络线上的功率振荡,使振荡在数秒内得以稳定;方案A比方案B的控制效果好,说明较多的广域测量信息在控制上效果更好.
图 10
图 10 发电机与联络线功率的响应曲线(运行方式I′)
Fig.10 Response curves of generator and tie-line power (Operation mode I′)
为了进一步验证本文方法的适应性,在运行方式Ⅱ′条件下,发生相同故障时的仿真曲线如图11所示. 可以明显看到采用所提方法设计的广域PSS在运行方式改变后依然能够增大系统的阻尼,使系统在受扰动后重新回到稳定状态. 同理,在运行方式Ⅲ′条件下也可得到相同结论,说明所提方法是一种对不同运行方式具有一定的鲁棒性的广域协调控制策略.
图 11
图 11 发电机与联络线功率的响应曲线(运行方式II′)
Fig.11 Response curves of generator and tie-line power (Operation mode II′)
图 12
图 12 3种运行方式下系统的机电模式特征值分布图
Fig.12 Eigenvalue distribution of electromechanical mode under three operation modes
6. 结 论
(1)蝙蝠算法简单易实现,在寻优中具有较好的收敛性和准确性,能够寻找到全局最优点,具有较强的搜索能力.
(2)在目标函数中采用多个目标进行优化,考虑了PSS参数变化对机电模式特征值的综合影响,通过调节不同目标的权重来改善特征根的分布;
(3)算例仿真表明:该方法能够对电网进行广域优化协调控制,在抑制区域间振荡模式上,考虑广域控制策略要比本地控制效果更好;同时,较多的广域测量信息在控制上效果较好.
(4)该方法是一种对系统运行方式变化具有良好适应性和鲁棒性的广域PSS参数优化方法,适用于广域PSS参数的协调设计,也可用于PSS和FACTS阻尼控制器的协调设计.
参考文献
基于广域响应的电力系统暂态稳定控制技术评述
[J].
Review on power system transient stability control technologies based on PMU/WAMS
[J].
多重扰动下的跨区电网低频振荡研究
[J].DOI:10.3969/j.issn.1000-6753.2014.02.035
Research on low frequency oscillation of interconnected power grid based on multiple disturbances
[J].DOI:10.3969/j.issn.1000-6753.2014.02.035
大规模互联电网低频振荡分析与控制方法综述
[J].
A survey on analysis on low frequency oscillation in large-scale interconnected power grid and its control measure
[J].
基于阻尼转矩分析法的多广域阻尼控制器多模态交互影响分析
[J].
Interaction of multiple wide-area damping controllers based on DTA method
[J].
考虑交互作用的多阻尼控制器独立设计的控制环选择
[J].DOI:10.3969/j.issn.1000-6753.2016.04.019 [本文引用: 1]
Control loops selection for independent design of multiple damping controllers with interactions considered
[J].DOI:10.3969/j.issn.1000-6753.2016.04.019 [本文引用: 1]
多机电力系统广泛配置PSS的可行性研究
[J].
Study on the feasibility of wide usage of PSS in multi-machine power system
[J].
PSS控制过程中的借阻尼现象与负阻尼效应
[J].
Borrow damping phenomena and negative damping effect of PSS control
[J].
Improved model-free adaptive wide-area coordination damping controller for multiple-input-multiple-output power systems
[J].DOI:10.1049/iet-gtd.2016.0069 [本文引用: 1]
Wide-area robust coordination approach of HVDC and FACTS controllers for damping multiple interarea oscillations
[J].DOI:10.1109/TPWRD.2012.2190830
计及广域信号多时滞影响的电力系统附加鲁棒阻尼控制
[J].
Additional robust damping control of wide-area power system with multiple time delays considered
[J].
A coordinated design of PSSs and UPFC-based stabilizer using genetic algorithm
[J].DOI:10.1109/TIA.2014.2305797 [本文引用: 1]
Bat algorithm: a novel approach for global engineering optimization
[J].DOI:10.1108/02644401211235834 [本文引用: 1]
Capacity configuration optimisation for stand-alone micro-grid based on an improved binary bat algorithm
[J].DOI:10.1049/joe.2017.0696 [本文引用: 1]
An optimized K-means clustering technique using bat algorithm
[J].
考虑噪声的电力系统低频振荡辨识方法
[J].
Low frequency oscillation identification method of power system considering its noise
[J].
基于包络线拟合的低频振荡性质在线判别
[J].DOI:10.7500/AEPS20131022005 [本文引用: 1]
On-line identification of low-frequency oscillation properties based on envelope fitting
[J].DOI:10.7500/AEPS20131022005 [本文引用: 1]