点群选取是地图综合的重要组成部分,指在地图比例尺缩小的过程中从原始点群中抽取含有一定数量点的子集合,其目的是在点数目减少的情况下尽量正确表达点群的整体信息[1].
点群选取的相关算法已比较成熟,具有代表性的有基于Voronoi图及加权Voronoi图的点群选取算法[2-4]. 以上算法利用普通Voronoi图或加权Voronoi图表示点群的辐射范围,并以此为依据计算点群的选取概率,进而进行点的取舍. 其中用到的Voronoi图均将平面视为均匀空间,并假设任意2点可以通过1条直线或曲线直接相连[1, 4-7]. 但在实际地理空间中,各种地理要素之间的相互联系发生于网络路径,传统Voronoi图剖分忽略了点群之间的连接与通达是沿着道路网的路径距离的事实;不仅如此,已有算法均没有顾及相关道路对点群辐射范围的影响,而现实生活中,点群的辐射范围往往与其周边道路是紧密相关的,关联道路的通达程度及道路等级等都会影响点群的辐射范围.
1. 点群选取算法流程
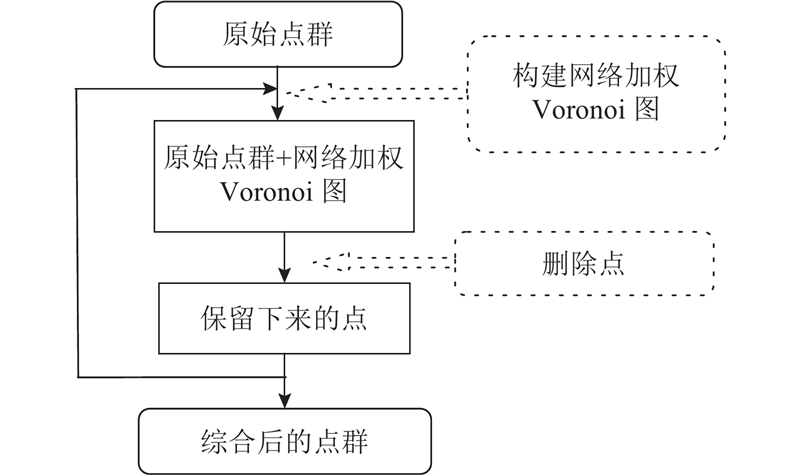
算法主要由两部分组成:1)构建原始点群的网络加权Voronoi图;2)以网络加权Voronoi图为基础,提出“同心圆”算法进行点的删除. 其主要流程如图1所示.
图 1
图 1 基于网络加权Voronoi图的点群选取算法流程图
Fig.1 Flowchart of point cluster selection algorithm based on weighted network Voronoi diagram
2. 点群选取算法描述
2.1. 网络加权Voronoi图的构建
城市空间通达、连接是沿着道路网伸展的,在此基础上对网络空间进行Voronoi图划分,即构建网络加权Voronoi图,是分析点群辐射范围的重要步骤. 本研究参考Ai等[12]提出的水流扩展思想构建点群的网络加权Voronoi图,下面对其构建过程进行描述.
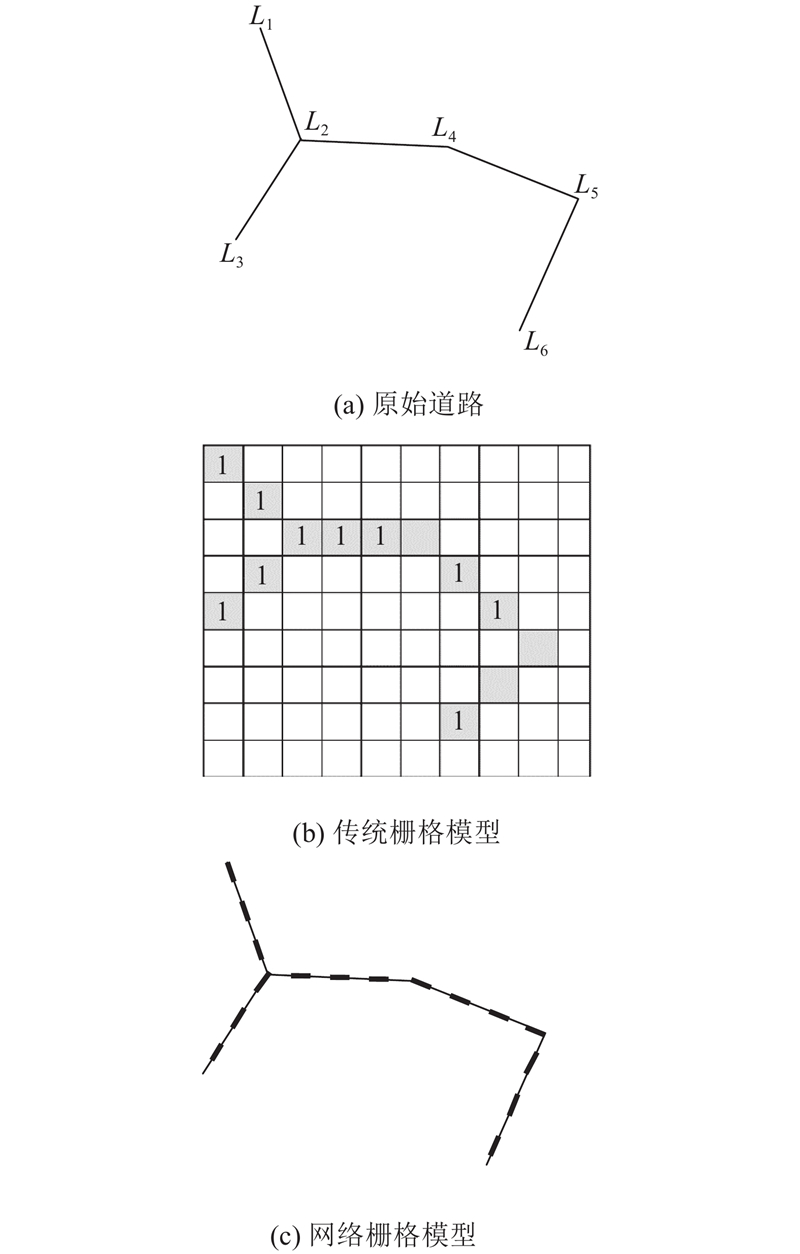
2.1.1. 网络图栅格化
图 2
图 3
2.1.2. 扩展操作
图 4
1)点的权重越大,以其为发生元的支流的扩展速度越快:
式中:LB为该支流方向上的扩展步长,k1为权重为1的发生元在弧段上的扩展步长,W(p)表示该点的权重函数.
2)扩展过程中相应的弧段权重越高,其上经过的支流扩展速度越快:
式中:k2为权重为1的道路段上支流的扩展步长,W(x)表示该弧段所在道路段的权重函数.
3)扩展过程会受弧段方向的制约,表现为支流只能沿着弧段的方向扩展:
式中:k3表示栅格单元长度,F(P1,P2)为判断支流方向P1与道路段通达方向P2是否一致的函数(若一致,则此函数值为1;若否,则为0).
2.1.3. 生成网络加权Voronoi图
综上所述,网络加权Voronoi图的生成步骤(见图5)如下.
图 5
1)网络图栅格化. 将道路网按照道路交叉点划分为不同的网络弧段,然后对弧段进行网络栅格化处理.
2)初始化发生元. 将距离点群距离最近的栅格单元定义为扩展操作的初始发生元.
3)网络扩展:以初始发生元为起始弧段,以点群权重、相关联弧段权重及弧段方向为依据,沿着对应的弧段方向向外扩展一定步长,并更新栅格标识属性.
4)判断当前发生元,若其为扩展栅格,则继续沿着对应方向向外扩展,直至发生元的所有邻近栅格均为占有栅格.
2.2. 点的删除
2.2.1. 点群选取中各类信息保持策略
点群综合的关键在于综合后的点群能够较好地保持原始点群的各类信息. 为了在充分顾及点群权重的基础上,保证原始点群信息的正确传输,算法采取了如下策略.
1)统计信息:采用开方根定律确定因比例尺变化而综合后的点的数目[16].
式中:N0为原始点群数目;N′为综合后的点群数目;M0为原始地图比例尺分母;M′为目标比例尺分母.
2)专题信息:将点的权值作为点群选取的基本依据. 通过分析,将以下2个因素设为点群重要性衡量指标,并将其作为点群权重衡量指标,即:
图 6
图 6 点群的网络加权Voronoi多边形及其扩展弧段
Fig.6 Weighted network Voronoi polygons and extended segments of point cluster
式中:Pi1表示点在点群中的网络Voronoi多边形面积所占比,Ai为第i点的网络Voronoi多边形面积.
b)点群的扩展弧段总长度. 一方面,在网络扩展过程中,点及其相关道路网的权重决定了网络扩展速度,而网络扩展速度直接影响着扩展弧段总长度. 因此,点群对应的扩展弧段总长度可以在一定程度上反映点群及其相关道路网的重要性程度;另一方面,道路网局部密度也会对网络扩展结果产生影响,而这种局部密度差异也可以通过点的扩展弧段总长度反映出来. 如图6所示,点P2所在局部区域道路网密度明显高于点P1所在道路网局部密度,导致在同样的扩展速度下,点P2对应的网络Voronoi多边形面积小于点P1对应的网络Voronoi多边形面积,这种局部密度差异可以用“由点P2扩展的弧段总长度大于点P1”来表示. 点群的扩展弧段总长度不仅能够反映点群的重要性程度,还可以作为网络扩展过程中道路网局部密度差异的一种表现. 因此,将点群的扩展弧段总长度作为其权重衡量的另一指标:
式中:Pi2表示点在点群中的扩展弧段总长度所占比,li为第i点的扩展弧段总长度.
在以上2个点群权重衡量指标的基础上,算法遵循“网络Voronoi多边形面积越大或其扩展弧段总长度越长,其所对应的点越容易保留”的规则进行点群选取. 并将点群分为3种类型:高等级必须保留(Ⅰ型:对应的网络Voronoi多边形面积较大或者扩展弧段总长度较大)、低等级直接舍弃(Ⅱ型:对应的网络加权Voronoi图面积及扩展弧段总长度都较小)以及介于两者之间参与选取竞争(Ⅲ型)[18].
式中:mi'为点i的相对密度,mi为点i的绝对密度,mi=1/Ai.
2.2.2. 点的删除
(1)根据式(1)开方根定律[9]求得综合过程中预删除点的数目:
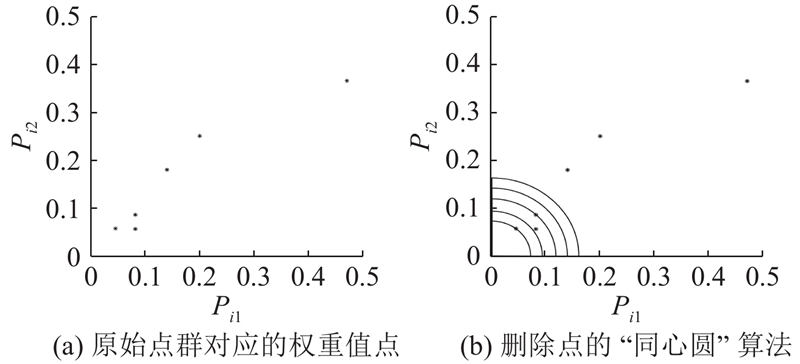
(2)利用式(5)、(6)求得点群中所有点的Pi1及Pi2. 将其对应标示在以Pi1为横坐标,Pi2为纵坐标的平面直角坐标系中(见图7(a)),并将其称为权重值点. 此时权重值越小的点(Ⅱ型点)越靠近坐标原点,因此采用以原点为圆心作1/4同心圆的方法,依次选取权重值较小的点,对其进行邻近关系判断和删除操作,本文称其为“同心圆”法.
图 7
图 7 删除点的“同心圆”算法
Fig.7 Method of ‘concentric quadrants’ in point deletion process
(3)以坐标原点为原点,以权重值点与坐标原点距离的最小值为初始半径在坐标系中画1/4圆,将位于圆弧上的权重值点对应的点标记为“删除”,并“固定”其多边形邻居点.
(4)以平面坐标系中权重值点之间的最小平面距离为增量,更新半径值,以原点为圆心在坐标系内作1/4同心圆(如图7(b)所示),对于其圆弧上以及其与前一次的同心圆构成的圆环内的“自由”点,若其所有邻居点均没有被标记为“删除”,则将其标记为“删除”并“固定”其所有邻居点. 比较n与被标记为“删除”的点的个数,若n值较大,则重复4);若两者相同,则转至6);否则转至5).
(5)将4)中添加了 “删除”标记的点改为 “自由”,将这些点按照网络Voronoi多边形面积降序排序,依次对位于队列尾端的点进行判别并添加“删除”标记,并对其网络加权Voronoi多边形邻居添加“固定”标记,直至标记为“删除”的点的总个数等于n时转6);
(6)在原始点群中删除被标记为“删除”的点,剩余点群则为选取后的结果,算法结束.
3. 实验与讨论
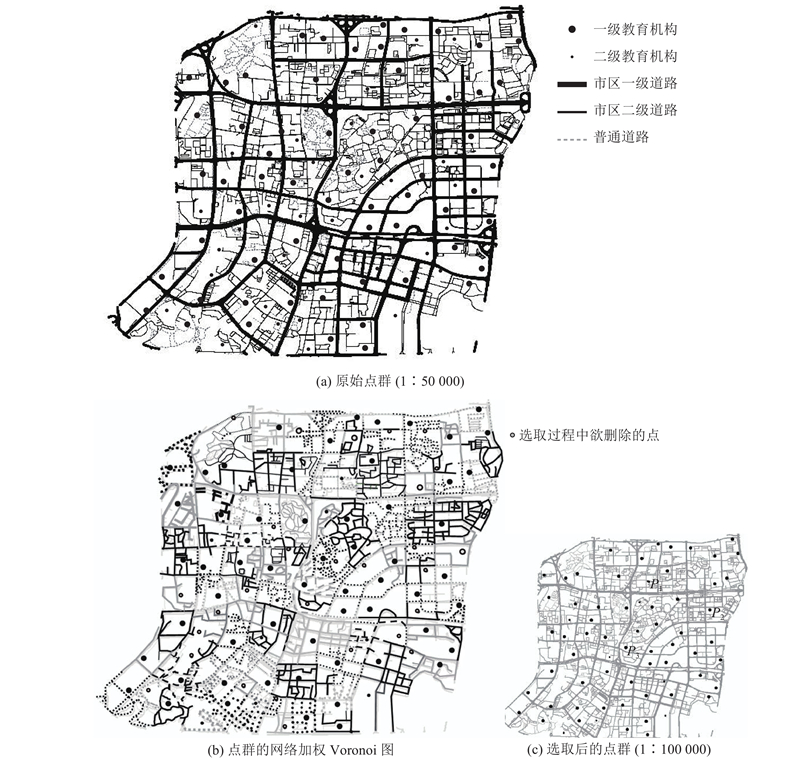
选取深圳市某区域96个教育机构进行实验,其中,按照规模大小将其分为一级教育机构63个,二级教育机构33个;参与分析的道路网络由3级共4 652条道路段组成,其中市区一级道路2 217段,市区二级道路1 765段,一般道路670段. 原始地图比例尺为1∶50 000(见图8(a)),目标比例尺为1∶100 000.
图 8
图 8 基于网络加权Voronoi图的点群选取实验
Fig.8 Experiment of point cluster selection based on weighted network Voronoi diagram
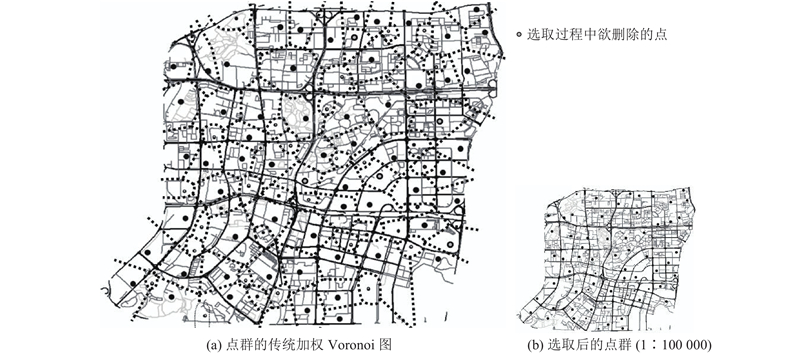
如图9所示为利用传统加权Voronoi图(multiplicatively weighted Voronoi diagram,MWVD)对同样的点群数据进行实验的结果.
图 9
图 9 基于传统加权Voronoi图(MWVD)的点群选取实验
Fig.9 Experiment of point cluster selection based on multipcatively weighted Voronoi diagram (MWVD)
算法对2组实验过程中原始点群各类信息的保持程度进行了计算,其中,各类信息的传输评价标准如下.
1)统计信息:
式中:Ng为综合后点的数目,No为按照开方根定律应该保留的点的数目,Ds越小,统计信息传输越好.
2)专题信息:
式中:
3)拓扑信息:
式中:
4)度量信息:
其中,Pg为综合后的点群分布边界多边形面积,Po为综合前的原始点群分布边界多边形面积,Dm越小,密度信息传输越好.
根据式(8)~(11),得到2组实验中各类信息的传输程度量化表示如表1所示.
表 1 实验中各类信息的传输程度
Tab.1
| 算法 | Ds | Dth(归一化后) | Dtp | Dm/% |
| 基于MWVD的点群选取算法 | 1.00 | 0.062 | 1.563 | 1.324 |
| 本文点群选取算法 | 0.21 | 0.154 | 1.612 | 1.483 |
根据以上实验及表1可以得出:
1)基于网络加权Voronoi图的选取算法,较好地保持了原始点群的各类信息,尤其是对于统计信息与专题信息的保持与传输明显优于传统算法;在点群拓扑信息的保持策略中,由于网络加权Voronoi多边形邻居点较Voronoi多边形邻居点更符合实际地理空间特征,提出的算法对于点群拓扑信息保持程度优于传统算法,但为了更好地展示算法,实验所选点群的分布比较均匀,空间拓扑关系比较简单,从表1可以看出,这种优势不太明显;在点群度量信息的传输中,由于采用了相对密度保持策略,而利用网络加权Voronoi图与Voronoi图对于相对密度的影响区别不大,提出的算法与传统算法在度量信息的保持程度上差别不大,但由于网络加权Voronoi多边形面积较Voronoi多边形面积更能代表点群的辐射范围大小,提出的算法更具现实意义.
2)将网络加权Voronoi多边形面积及扩展弧段总长度作为衡量点群权重的两大指标引入点群选取,充分顾及了点群重要性、相关道路网权重及道路网局部密度对点群选取结果的影响.
3)网络加权Voronoi图的引入,使得点群选取算法既考虑了地理实体的空间分布等几何属性,又顾及了相关道路等级等非几何属性,使得选取结果更加合理.
4)基于网络加权Voronoi图的算法顾及到了点群关联道路的连通性,使得连通性较好的道路相关联的点具有较大的辐射范围,与实际情况比较吻合.
5)提出的点群选取算法利用“同心圆”方法解决了点群删除过程中的多因子集成问题,算法思路简单,较好地解决了点群的取舍问题.
4. 结 语
本文提出的基于网络加权Voronoi图的点群综合算法以网络路径代替传统的欧式距离,融入了相关道路段的权重、方向等因素;在点的删除过程中,综合了点对应的网络加权Voronoi多边形面积及扩展弧段总长度对点的重要性的影响;在此基础上,提出了“同心圆”方法,较好地解决了2种因子影响下的点群取舍问题. 综合后的点群较好地保持了原始点群的各类信息;较好地顾及了点群权重、点群分布位置及点群相关联道路属性特征,综合结果更加符合实际地理空间特征.
参考文献
利用层次Voronoi图进行点群综合
[J].
Point group generalization method on hierarchical Voronoi diagram
[J].
基于Voronoi图的点群目标普适综合算法
[J].DOI:10.3969/j.issn.1006-8961.2005.05.017 [本文引用: 1]
A generic algorithm for point cluster generalization based on Voronoi diagrams
[J].DOI:10.3969/j.issn.1006-8961.2005.05.017 [本文引用: 1]
地图点群综合的加权Voronoi算法
[J].
A MWVD-based algorithm for point cluster generalization
[J].
An algorithm for point cluster generalization based on the Voronoi diagram
[J].DOI:10.1016/j.cageo.2007.07.008 [本文引用: 2]
基于Kohonen网络的点群综合研究
[J].
Points group generalization based on Konhonen Net
[J].
基于邻近图的点群层次聚类方法的研究
[J].
Hierarchical clustering method of group of points based on the neighborhood graph
[J].
两种地图点群综合算法的比较
[J].DOI:10.3969/j.issn.1006-7949.2015.06.010 [本文引用: 1]
Comparison of two point cluster generalization algorithms
[J].DOI:10.3969/j.issn.1006-7949.2015.06.010 [本文引用: 1]
Generalized network voronoi diagrams: concepts, computational methods, and applications
[J].DOI:10.1080/13658810701587891 [本文引用: 1]
基于局部聚类的网络Voronoi图生成方法研究
[J].
A method for integrating network Voronoi and spatial clustering
[J].
基于网络Voronoi图的大规模多仓库物流配送路径优化
[J].
Large scale multi-depot logistics routing optimization based on network Voronoi diagram
[J].
网络加权Voronoi图的动态构建
[J].
The dynamic construction of network weighted Voronoi diagram
[J].
Generation of constrained network Voronoi diagram using linear tessellation and expansion method
[J].DOI:10.1016/j.compenvurbsys.2015.02.001 [本文引用: 1]
水流扩展思想的网络空间Voronoi图生成
[J].
Algorithm for constructing network Voronoi diagram based on flow extension ideas
[J].
点云曲面空间网格化加密求交算法
[J].
Intersection algorithm of point cloud surface by spatial mesh and refinement
[J].
The principles of selection
[J].DOI:10.1179/caj.1966.3.1.10 [本文引用: 1]
基于约束Delaunay三角网的线, 面群目标分布边界计算
[J].DOI:10.3969/j.issn.1006-7949.2015.05.009 [本文引用: 1]
Computation of the boundaries of linear/polygonal groups based on constrained Delaunay triangulation
[J].DOI:10.3969/j.issn.1006-7949.2015.05.009 [本文引用: 1]
顾及道路目标Stroke特征保持的路网自动综合方法
[J].
A method of road network generalization considering stroke properties of road object
[J].
Qualitative measures for spatial information of maps
[J].DOI:10.1080/13658810210149416 [本文引用: 2]