物体和物体之间的联系构成网络,这样的联系无处不在,网络是一种灵活而通用的数据结构. 在现实世界中,许多类型的数据都可以抽象成网络,如社交网络、公路网络、万维网、物联网、生物网络、语言网络等. 对网络进行分析可以提取有价值的信息,其中一个重要的问题就是如何对数据进行表示. 网络表示学习给网络分析任务带来极大的便利,也是网络原始数据和网络应用任务的桥梁[1].
已有研究主要针对同构网络,对异构信息网络的相关研究较少.本文针对异构信息网络中节点和节点间链接关系类型不同的特点,选取典型的异构信息例子,对异构信息网络中节点相似性大小进行建模,利用深度学习提取复杂特征的特点,对传播概率矩阵进行降维,研究基于传播概率矩阵的异构信息网络表示学习算法在分类、聚类、可视化上的效果.
1. 基于传播概率矩阵的异构信息网络表示学习模型
1.1. 相关定义
基于传播概率矩阵的异构信息网络表示学习(heterogeneous information network representation learning based on transition probability matrix,HINtpm)的相关定义如下.
定义1 异构信息网络(heterogeneous information network,HIN):给定一个图
图 1
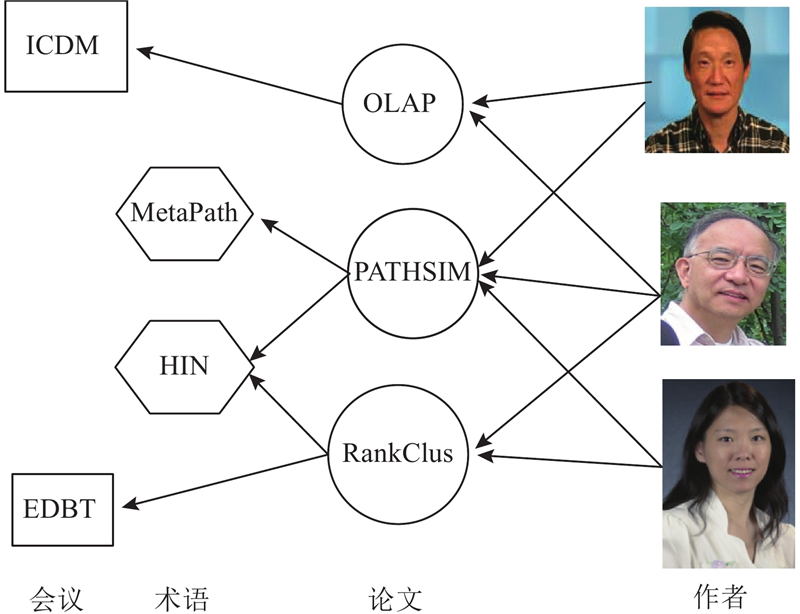
图 1 典型异构信息网络(HIN)举例:DBLP
Fig.1 Example of typical heterogeneous information network (HIN): DBLP (digital bibliography & library project)
定义2 异构信息网络模式(HIN Schema):给定一个HIN G=(V,E),映射函数
图 2
定义3 元路径Meta Path:给定HIN G=(V,E),元路径Path是定义在网络模式TG=(L,R)上的:
定义4 邻接矩阵W:在图G中,对于一个无权重的无向图而言,仅当顶点Vi和顶点Vj之间存在一条边时Wij=1,否则Wij=0.
定义5 度数矩阵D是一个对角矩阵,矩阵每一行对角线上的值均为邻接矩阵W每一行的和,其余值为0.
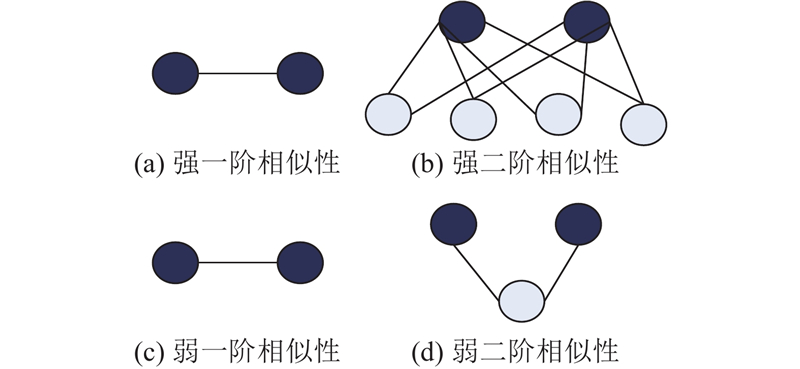
定义6 一阶相似性:在同构信息网络中,一阶相似性由直接相连的节点决定,权重越大,节点越相似.
定义7 二阶相似性:在同构信息网络中,二阶相似性由相邻节点共同邻居的个数来决定,共同邻居数量越多,认为相邻的2个节点相似性越高.
1.2. 基于传播概率矩阵的相似性计算
同构信息网络上节点的相似性可通过共同邻居个数、传播概率矩阵等来计算,但是该计算方法忽略了对象和链接间类型的细微区别. 因为异构信息网络中节点和链接具有多样性,所以在异构信息网络中不能直接应用同构网络中的相似性规则. 即使是相同的对象,在不同的元路径下语义也不同,而不区分语义地评价相似性是没有意义的,且不是所有节点间的相似性大小都有意义和可解释的.
异构信息网络中节点相似性大小可以通过元路径来计算,因此可以用元路径上节点传播概率矩阵的相似性度量来表示节点相似性大小. 然而,多数应用场景都是寻找网络中相似的对等对象,即对象类型相同,如寻找领域内相似的作者,寻找风格相似的演员,或者寻找功能相同和受欢迎程度相似的产品. 同种类型的对象间的关系是对称的, HINtpm算法限定于对称的元路径.
利用元路径来计算节点相似性的算法还有PathSim[22],可以捕捉到对等对象之间的细微之处,为对称路径给定一对称的元路径P. 对于同类型对象x和y之间的PathSim定义如下:
式中:
为了计算节点相似性,给定一条如式(1)所示的元路径. 定义Wij为li、lj的邻接矩阵,则元路径上的可交换矩阵可由邻接矩阵相乘得到:
例如DBLP数据集中选取元路径A-P-C-P-A(如图3所示),其中A代表作者,P代表论文,C代表会议. WAP表示A、P的邻接矩阵,则可交换矩阵:
图 3
根据定义5,可得度数矩阵:
其中,K为同构网络中节点的邻接矩阵,|K|=m=n.
将式(5)改进为适合异构信息网络的度数矩阵:
式中:M为可交换矩阵,例如元路径为A-P-C-P-A. 假设在邻接矩阵Wij中,从顶点li到顶点lj的传播概率是成比例的,则适合异构信息网络的传播概率矩阵为
图 4
图 4 同构信息网络中的一阶、二阶相似性
Fig.4 First-order and second-order similarity of homogeneous information network
将同构信息网络中一阶相似性、二阶相似性推广到异构信息网络中节点的一阶相似性、二阶相似性. 定义异构信息网络节点一阶相似性大小为异构信息网络中元路径上相邻的同类型的节点间的传播概率大小.定义异构信息网络节点二阶相似性大小为异构信息网络中元路径上间隔一个同类型的节点间的传播概率大小.
1.3. 深层神经网络
深度学习采用非线性的激活函数,使得深度学习算法能提取非线性的复杂特征,正好可以用来提取传播概率矩阵中的非线性的特征,达到降维的目的.
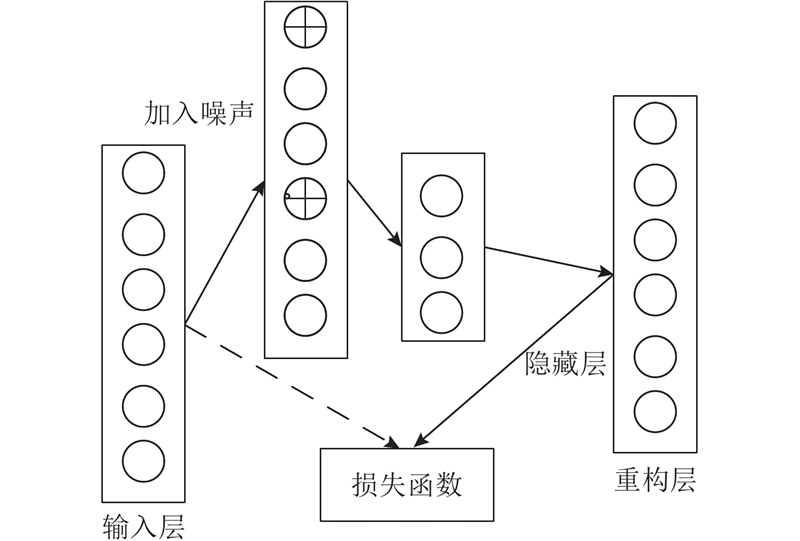
自动编码器能自动提取输入数据中的特征,是一种无监督的学习算法,使用反向传播算法,并让目标值等于输入值. 自动编码器分为2个部分:编码和解码. 在编码阶段,将输入数据通过函数
式中:
其中,
损失函数采用平方差,即输入层和重构层实例差值的平方:
式中:a为实例总数. 模型HINtpm采用的是降噪自动编码,即在输入的数据加上噪声以使训练的数据接近测试数据,增加降噪自动编码器的鲁棒性,防止过拟合.
使用的激活函数为ReLU:
降噪自动编码器模型如图5所示。
图 5
综上,完整HINtpm算法的流程如下.
输入 HIN G=(V,E).
1. 得到邻接矩阵
2. 计算可交换矩阵:
3. 计算度数矩阵:
4. 计算概率矩阵
5. 一阶相似性:S1=S;计算二阶相似性:S2=S1S1T,计算传播概率矩阵St=S1+S2。
用降噪自动编码器对St进行降维。设置降噪自动编码器学习率learningrate=0.001,隐藏层维度为128,每批训练向量大小batchsize=64.
输出 网络节点的向量表示.
2. 实验结果与分析
2.1. 数据集和HINtpm参数设置
(1)DBLP数据集.
从DBLP数据集中抽取一个子网络,子网络中有1 586位作者以及这些作者的10 353篇论文,其中的论文来自18个会议;作者来自4个领域:Data Base数据库、Information Retrieval信息检索、Data Mining数据挖掘、Machine Learning机器学习.
(2)AMiner数据集.
实验时,从AMiner中抽取一个子网络. 子网络包括来自4个不同领域的4 000位作者,75 184篇论文.
(3)HINtpm参数设置.
降噪自动编码器隐藏层的维度为128维,即所得节点表示的维度为128维. 实验中,在2个数据集上选取的元路径都为A-P-C-P-A,由于是对作者进行分类聚类,根据经验认为,在相同领域上发表论文数量越多的作者为同个类别的可能性更大.
2.2. 对比的节点特征量表示算法
(1)DeepWalk.
受到自然语言word2vec的启发,Perozzi等于2014年提出DeepWalk[20]. DeepWalk在网络中截断随机游走得到很多序列,这些序列相当于自然语言中的句子,然后对序列中的节点对用层级softmax和Skip-gram进行概率建模,使序列似然概率最大,通过随机梯度下降学习参数. 实验中,使用默认参数设置,例如窗口大小w=5,随机游走序列长度t=40,节点表示的维度为128.
(2)Node2vec.
Node2vec[21]定义了2个参数p和q,使随机游走在BFS和DFS中达到一个平衡,能保留节点局部和宏观的信息,具有很高的适应性. 实验中使用默认参数设置,p=q=1.0,所得节点表示的维度为128.
(3)Metapath2vec.
Metapath2vec通过元路径的方式来指导随机游走,构造节点的邻居节点集合,然后基于异质的skip-gram模型得到节点的向量表示. 节点表示维度为128,邻居节点大小为7,随机游走序列长度为150,负抽样大小为5.
2.3. 分类实验效果与分析
表 1 不同算法在DBLP数据集上的分类准确率
Tab.1
| 算法 | R=10% | R=20% | R=30% | R=40% | R=50% | R=60% | R=70% | R=80% | R=90% |
| DeepWalk | 0.655 0 | 0.713 9 | 0.754 8 | 0.743 9 | 0.780 7 | 0.768 0 | 0.788 4 | 0.795 6 | 0.786 2 |
| Node2vec | 0.653 5 | 0.735 5 | 0.764 4 | 0.772 7 | 0.783 1 | 0.761 7 | 0.781 5 | 0.786 2 | 0.817 6 |
| Pathsim | 0.790 2 | 0.816 8 | 0.827 5 | 0.826 7 | 0.824 5 | 0.833 1 | 0.833 4 | 0.830 2 | 0.888 1 |
| Metapath2vec | 0.866 2 | 0.896 9 | 0.888 4 | 0.896 0 | 0.897 6 | 0.907 1 | 0.911 8 | 0.920 1 | 0.880 5 |
| HINtpm | 0.893 6 | 0.914 3 | 0.926 7 | 0.929 8 | 0.929 9 | 0.937 1 | 0.949 6 | 0.944 3 | 0.941 5 |
| HINtpm0 | 0.897 3 | 0.925 3 | 0.935 3 | 0.926 1 | 0.938 1 | 0.945 0 | 0.945 2 | 0.939 0 | 0.968 6 |
表 2 不同算法在AMiner数据集上的分类准确率
Tab.2
| 算法 | R=10% | R=20% | R=30% | R=40% | R=50% | R=60% | R=70% | R=80% | R=90% |
| DeepWalk | 0.858 4 | 0.873 0 | 0.888 5 | 0.898 4 | 0.907 4 | 0.910 6 | 0.915 2 | 0.910 0 | 0.902 5 |
| Node2vec | 0.888 6 | 0.914 6 | 0.923 0 | 0.930 4 | 0.940 4 | 0.944 6 | 0.943 7 | 0.932 8 | 0.935 0 |
| pathsim | 0.954 4 | 0.965 8 | 0.997 17 | 0.971 5 | 0.972 1 | 0.974 8 | 0.979 2 | 0.980 0 | 0.982 5 |
| Metapath2vec | 0.898 5 | 0.928 5 | 0.935 2 | 0.937 6 | 0.935 2 | 0.939 9 | 0.940 5 | 0.953 9 | 0.944 0 |
| HINtpm | 0.947 5 | 0.961 4 | 0.960 3 | 0.963 7 | 0.961 0 | 0.963 8 | 0.969 7 | 0.975 4 | 0.984 3 |
| HINtpm0 | 0.963 6 | 0.967 6 | 0.969 7 | 0.976 8 | 0.976 7 | 0.975 6 | 0.983 5 | 0.985 9 | 0.985 0 |
2.4. 聚类实验效果与分析
聚类所用算法为K-Means,如表3所示为不同算法得到的节点表示的聚类效果,用NMI进行评价.
表 3 不同算法在DBLP和AMiner数据集上的标准化互信息(NMI)对比
Tab.3
| 算法 | NMI-DBLP | NMI- AMiner |
| DeepWalk | 0.483 4 | 0.781 8 |
| Node2vec | 0.499 0 | 0.831 5 |
| Metapath2vec | 0.570 7 | 0.595 8 |
| pathsim | 0.334 1 | 0.600 4 |
| HINtpm | 0.612 9 | 0.831 7 |
| HINtpm0 | 0.608 6 | 0.802 0 |
从表3可知,HINtpm算法得到的节点表示的聚类效果总体而言优于DeepWalk、Node2vec、Metapath2vec得到的节点表示的聚类效果.实验证明,HINtpm算法得到的节点表示可以用于异构信息网络聚类应用任务.
2.5. 可视化实验效果与分析
图 6
图 6 不同算法在AMiner数据集上的可视化效果
Fig.6 Visual effect of different algorithms on database AMiner
DeepWalk和Node2vec算法没有考虑到异构信息网络中节点和边类型的多样性,在异构信息网络上不适用。从前面的实验结果可知,HINtpm算法能学习到异构信息网络中节点和边类型的不同.
3. 结 语
本文介绍了一种基于概率传播矩阵的异构信息网络的表示学习算法,利用异构信息网络元路径上节点传播概率来表示节点相似性大小,然后对于得到的传播概率矩阵通过自动编码器的降维得到网络的节点表示. 实验证明:对比DeepWalk、Node2vec、metapath2vec算法,提出的HINtpm算法考虑了异构信息网络中节点的相异性,能很好地学习到异构信息网络中节点的表示,学习到的异构信息网络的节点表示在不同训练集比例下的节点分类准确率上有3%~24%的提升,在聚类NMI上有0~13%的提升. 但是,在本算法的计算过程中,随着节点数量的增加,矩阵维度线性增加;由于矩阵是整个直接存储在计算机内存中,计算机内存以节点数量的平方增加.
参考文献
网络表示学习综述
[J].
Network representation learning: an overview
[J].
Nonlinear dimensionality reduction by locally linear embedding
[J].DOI:10.1126/science.290.5500.2323 [本文引用: 1]
Word2Vec
[J].DOI:10.1017/S1351324916000334 [本文引用: 1]
PathSim: meta path-based top-K similarity search in heterogeneous information networks
[J].