不确定因素普遍存在于复杂装备优化设计过程中,工况载荷、结构几何尺寸的不确定可能导致装备结构性能的改变,因此优化设计过程必须合理考虑不确定因素的影响[1]. 国内外研究人员分别从概率可靠性优化、区间集合理论等方面对优化设计过程中存在的不确定进行了研究.
概率可靠性优化方面:Seshadri等[2]研究了设计参数的概率分布,采用密度匹配及高斯核估计方法求解翼型不确定设计问题. Lin等[3]利用传统的可靠性系数方法及改进的可靠性系数处理优化设计过程中的概率约束问题. Deb等[4]将传统的可靠性概念与进化算法相结合,阐述了进化算法在可靠性求解中的应用. Sinha[5]采用近似矩与可靠性指数方法,利用遗传算法计算了车辆耐撞性及乘员安全的优化问题. 概率可靠性分析需要足够的样本数据以得到设计变量的准确概率分布情况,在实际工程问题中,样本数据的获取十分复杂,样本数据的缺失使得设计变量参数分布与真实结果存在较大误差,进而影响概率可靠性分析方法的优化计算结果.
区间集合理论方面:姜潮[6]提出了一种改进的区间可能度方法,根据区间的位置关系将区间可能度归纳为6种不同的情况. Cheng等[7-9]在改进的区间可能度方法基础上,提出了区间约束违反度的概念,并构建了一种直接求解非线性区间优化的方法,因而不需要将其先转换为确定性优化问题. Jiang等[10-11]对混合不确定模型进行了研究,采用随机分布处理不确定性,将分布函数中的一些关键参数以区间表征并构造2种混合可靠性模型,对概率转换过程进行单调性分析,最终采用2种有效的算法来求解2种混合可靠性模型,实现区间不确定问题的求解. 区间集合理论优化方法主要采用嵌套优化方法处理不确定目标函数及约束函数,通过迭代寻优获取最优设计变量. 工程设计领域中优化设计模型通过复杂的数值计算过程获取,模型求解耗时长,并且区间扩张现象[12]在优化求解过程中会使结果保守失真. 为解决上述问题,Jiang等[13]提出一种基于IP-GA的双层嵌套优化算法,将区间不确定优化转化为确定性优化. 张德全等[14]针对分布参数为区间的一类随机不确定问题,提出了一种求解时变可靠性的区间PHI2方法,可以获得结构在设计周期内的时变可靠性区间. Jiang等[15]针对随机和区间变量的混合不确定优化问题,将具有足够信息的不确定参数以随机分布形式表征,对另外信息有限的不确定参数则给出其变化区间,建立了混合可靠度等效模型并构造了具有高效率收敛性能的求解算法. Han等[16]通过引入响应面方法提出了一种新的混合可靠性方法,通过使用二次多项式和修正的轴向实验设计方法构建极限状态函数的响应面模型,并利用高效解耦方法求解近似混合可靠性问题,并通过更新策略提高响应面模型的精度,进而保证可靠性分析精度. Lim等[17]采用Akaike信息准则(Akaike information criterion, AIC)及极大似然函数确定不确定变量的分布参数,并对白车身及发动机车架进行了优化. Peng 等[18-19]针对随机不确定变量、区间不确定变量的混合优化问题,采用AIC及证据理论确定区间变量的边界,利用Kriging模型对混合不确定优化问题进行建模. Sankararaman等[20-21]利用贝叶斯定理以及极大似然估计对稀疏混合不确定变量的分布进行估计. 由于区间集合理论方法的区间扩张现象引发计算结果失真现象,设计结果一般存在较多的冗余,采用嵌套优化方法处理区间扩张问题计算的可靠性指标与失效概率等较为准确,但存在计算迭代次数多、计算周期长的问题,优化计算过程要同时考虑区间扩张和嵌套优化造成的影响.
为解决数据缺失造成的稀疏混合不确定变量优化问题,提出一种基于Chebyshev逼近的稀疏混合不确定变量优化方法. 使用极大似然估计及贝叶斯信息准则确定稀疏混合不确定变量的最合适的分布,求取稀疏混合不确定变量的分布参数;基于Chebyshev逼近功能函数,获取多项式在区间变量上的极值,利用改进的HL-RF算法进行迭代求解,获取稀疏混合不确定变量的优化问题的可靠度指标及失效概率. 最后将提出的方法应用于高速压力机滑块的优化设计.
1. 稀疏混合不确定变量的量化
1.1. 稀疏混合不确定变量分布估计
不确定变量的量化是优化设计的前提,不确定变量包括随机不确定变量和认知不确定变量. 随机不确定变量一般可以采用常用的概率分布直接进行量化,采用等概率正态变换、Rosenblatt变换等将非正态分布的随机不确定变量转化为等效的独立正态分布变量. 当变量之间存在统计相关并且非正态分布时,也可采用Rosenblatt变换将其转换为独立的正态随机分布.
认知不确定变量由于统计数据的缺乏,不能以概率分布形式直接对其进行量化,常用区间分析、模糊集理论、证据理论和可能性理论等研究认知不确定变量. 如果变量包含离散采样点与区间变量,如
其中L和U为区间变量的下界与上界,称此类离散点与区间混合的设计变量为稀疏混合不确定变量,采用区间分析方法,令
存在的区间扩张现象会使计算结果失真,工程结构优化设计领域则表现为材料冗余、资源浪费. 对于包含离散变量及区间变量的稀疏混合不确定问题,合理估计离散点及区间变量从属的分布类型并确定其最合适的分布参数,是避免区间扩张现象导致计算结果失真的有效方法.
采用极大似然估计方法估计稀疏混合不确定变量分布参数值,将工程设计领域常用的概率分布作为候选分布,首先令稀疏混合不确定变量属于分布θ,分布参数为
从而相互独立的p个离散点yi(i=1,2,
在区间
在相互独立区间
综合式(1)~(4),在给定分布θ下,Y关于参数
求取似然函数
式中:
式中:num()为求
工程设计领域中常用分布有均匀分布、正态分布、对数正态分布、极值分布等,可以根据
1)正态分布:
式中:
2)均匀分布:
式中:bu为上界,bl为下界.
3)极值I型分布:
式中:
4)对数正态分布:
式中:u为对数均值,
5)F分布:
式中:
6)威布尔分布:
式中:s1为位置参数.
7)指数分布:
8)伽马分布:
式中:
1.2. 稀疏混合不确定变量概率密度
分别以不同分布类型估计Y的参数,计算其信息损失量,并选用Y的最合适的分布,进一步构造Y在其最合适的分布θ下对分布参数
由贝叶斯定理[22]获取不确定分布参数
稀疏混合不确定变量Y的概率密度函数采用非参数的全概率形式的函数表示:
由式(18)可以获取稀疏混合不确定变量Y的全概率形式密度函数,将稀疏混合不确定变量转化为具体的概率分布形式,采用一次二阶矩方法(first order second moment method,FOSM)求解含有稀疏混合不确定变量的结构可靠度问题.
2. Chebyshev响应逼近
根据式(19)获取递归形式的Chebyshev多项式:
定义在区间[−1,1]上的连续函数可以展开成Chebyshev级数为
式中:
式中:p为下标i1,i2,
式中:xj为插值点,xj=cos θj,θj=(2j−1)π/(2n+2),j=1,2,
多维Chebyshev多项式的插值点个数为(n+1)k,维数较高时,插值点对应系数计算量则会急剧增长,而采用n+1个插值点即可有效逼近
式(26)作为对包含稀疏混合不确定变量的响应函数的逼近多项式,采用一次二阶矩方法FOSM即可求解对应的可靠性指标与失效概率.
3. 稀疏混合不确定问题可靠性计算
采用Chebyshev多项式逼近含稀疏混合不确定变量的响应函数,并根据区间运算法则获取响应的极值函数,然后采用改进的HL-RF算法迭代求解获取的极值函数,获取稀疏混合不确定问题的可靠性指标及失效概率. 含有稀疏混合不确定变量的可靠度指标计算过程如下.
1)根据稀疏混合不确定变量Y,分别构建不同分布θi下关于相应参数
2)根据最适合的分布类型θ*及其对应参数
3)固定稀疏混合不确定变量为xs,令区间变量中a=Ymin,b=Ymax,xk为Chebyshev多项式在[−1,1]上的第k个采样点,其中:
对应的yk在区间[a,b]上采样点取值为
4)利用改进的HL-RF算法,将随机不确定变量与稀疏混合不确定变量的概率分布参数通过等概率正态变换、Rosenblatt变换等转化为满足独立的正态分布形式的变量,代入步骤3)获取的极值响应函数,通过式(27)~(29)迭代计算求解可靠度指标β与对应的变量U,获取最优的β*和U*,然后利用式(30)求解可靠度指标和失效概率.
令
4. 数值实例与压力机滑块设计实例
4.1. 稀疏混合不确定的数值实例
含有稀疏混合不确定的Rosenbrock公式[25]表示为
式中:x∈[−1,1],y∈{−1,−0.869,−0.502,−0.178,0.212 8,0.68,0.95,1,[−0.8,−0.4],[−0.3,0.2],[0.32,0.65],[0.70,0.92]}. 对应于8种分布的BIC值分别为8.900,13.255,14.640,12.240,10.591,12.000,11.240和12.400,选用BIC值最小的正态分布作为稀疏混合不确定变量y的最合适的分布类型,均值为0.2,标准差为0.3,即y~N(0.2,0.3),令n=3,将其按照本文方法展开的逼近多项式为
采用区间分析方法[26]获取Rosenbrock公式的展开多项式为
将区间分析方法与本文方法分别展开成3次多项式的逼近误差,误差计算结果ε如图1所示. 利用区间运算法则,式(32)与式(33)在区间x∈[−1,1]的下界和上界分别为
图 1
图 1 区间分析方法与Chebyshev逼近的误差对比
Fig.1 Error comparison between interval analysis method and Chebyshev approximation
Rosenbrock原函数根据区间运算法则获取的下界和上界为
将式(34)~(36)的下界作为功能函数分别代入改进的HL-RF算法中求取可靠度指标β、失效概率Pf以及失效概率与Rosenbrock函数的相对误差δ,如表1所示,可见本文方法获取的逼近多项式可靠度指标和最大失效概率更接近Rosenbrock原函数的相关指标.
表 1 数值算例可靠性分析对比
Tab.1
| 对比方法 | β | Pf | δ/% |
| 区间分析方法 | −0.65 | 0.742 2 | 1.41 |
| 本文方法 | −0.676 4 | 0.750 6 | 0.29 |
| Rosenbrock精确解 | −0.683 | 0.752 8 | — |
4.2. 高速压力机滑块优化设计实例
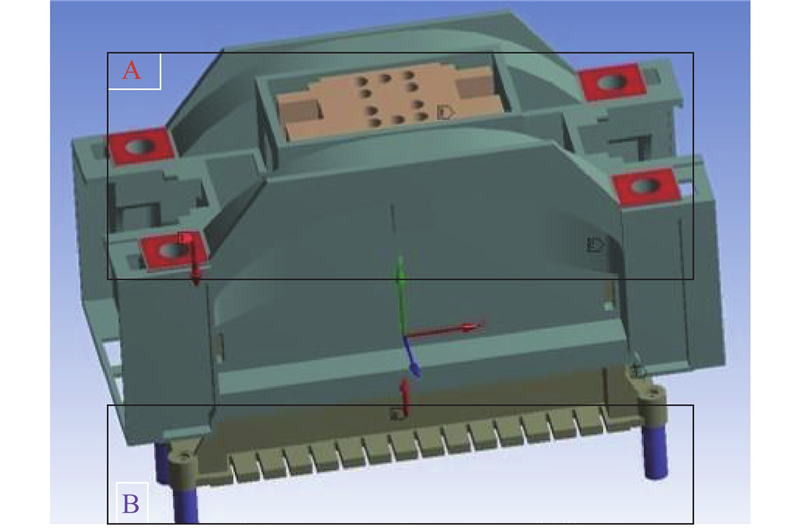
某型号宽台面超精密高速压力机滑块机构如图2所示,该滑块机构主要包括滑块、销钉、连杆、主轴和横梁等结构. 影响滑块刚度的主要变量有连杆间距x1、x2以及滑块高度x3,压力机滑块材料为HT300. 由于材料及加工工艺存在偏差,弹性模量E(x4)和泊松比v(x5)分别服从正态分布,根据该宽台面精密高速压力机的设计考核要求,极限状态函数要求最大质量m不大于1 300 kg,且当对滑块施加800 kN作用力时,最大应力σmax不大于58.5 MPa,根据此类宽台面超精密高速压力机滑块机构设计需求,压力机滑块优化函数构造如下:
图 2
图 2 宽台面超精密高速压力机及滑块数字样机
Fig.2 Digital prototype of wide table top ultra-precision high speed press machine and slider
表 2 分布类型及分布参数最优解
Tab.2
| 分布 | 参数1 | 参数2 | BIC值 |
| θ1:正态分布 | 600 | 5 | 29.34 |
| θ2:均匀分布 | 520 | 687 | 35.45 |
| θ3:极值I型分布 | 622 | 9 | 38.36 |
| θ4:对数正态分布 | 6.42 | 2.48 | 33.82 |
| θ5:F分布 | 5 | 2 | 42.23 |
| θ6:威布尔分布 | 590 | 85 | 27.25 |
| θ7:指数分布 | 600 | — | 38.56 |
| θ8:伽马分布 | 600 | 1.58 | 36.85 |
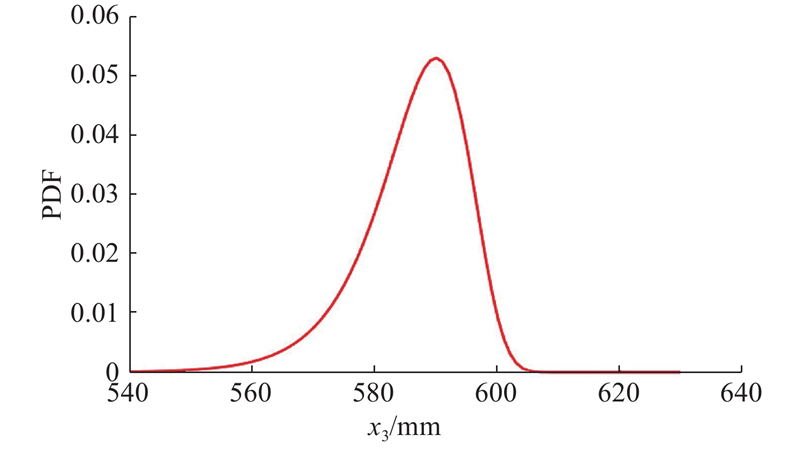
图 3
图 3 威布尔条件下变量x3的概率密度分布
Fig.3 Probability density distribution of variable x3 under Weibull conditions
获取采样点,对于变量x1、x2、x4、x5,采用下式获取采样点:
式中:i=1,2,4,5,ai和bi分别为第i个变量的边界值,取n=58,获得n+1=59组变量并将其重新排列,利用有限元仿真获取每组变量的质量与最大应力,变量最高次数为5次,构建式(37)中关于滑块功能函数g1与g2的Chebyshev逼近多项式如式(39)所示,将式(39)代入式(37)中,并采用改进的HL-RF算法迭代求解,求解结果如表3所示.
表 3 宽台面超精密高速压力机滑块设计优化对比
Tab.3
| 最优设计变量 | β | Pf | 设计目标 | |
| 区间分析 方法 | x1=412 mm | 1.982 | 0.023 | |
| x2=266 mm | m=1 287 kg, Pmax=53.48 MPa | |||
| x3=572 mm | ||||
| E=1.45×105 MPa | ||||
| v=0.25 | ||||
| 本文方法 | x1=366 mm | 2.10 | 0.018 | |
| x2=272 mm | m=1 201 kg, Pmax=53.44 MPa | |||
| x3=564 mm | ||||
| E=1.44×105 MPa | ||||
| v=0.24 |
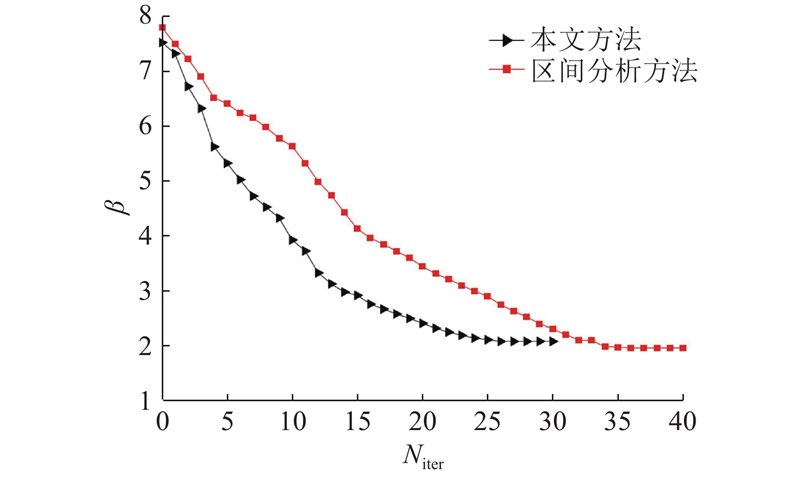
由图4 (图中Niter为迭代次数)可见,在对功能函数的迭代计算过程中,所提方法迭代30次即可收敛,对比方法仍然采用区间分析方法[26],迭代39次才能收敛. 由于所提方法与对比方法在迭代中采用同样的改进HL-RF算法以及NSGA-II算法,每次迭代耗时接近,所提方法的迭代效率较区间分析方法有了明显提高;此外,所提方法获取的可靠度指标为2.10,大于对比方法的1.982,因此所提方法求取的滑块参数比区间分析方法更加可靠. 如表3所示为采用区间分析方法[26]以及所提方法对功能函数迭代求解后的设计变量值、可靠度指标β、失效概率指标Pf. 分别将2种方法获取的设计变量构建数字样机并进行仿真分析,对滑块油缸接触部件及底座接触部件施加载荷,如图5所示,A框内端面为施加载荷区域,对4个端面施加800 kN的载荷并约束B框内的支撑杆,求解仿真分析结果目标值如表3所示,在功能函数满足设计需求情况下,采用本文方法最优解构建的数字样机较区间分析方法质量下降86 kg.
图 5
图 4
图 4 Chebyshev逼近及区间分析方法的可靠性求解迭代过程
Fig.4 Iterative process for reliability analysis using Chebyshev approximation and interval analysis method
5. 结 论
(1)本文提出了一种稀疏混合不确定变量量化方法,将稀疏混合不确定变量采用极大似然估计、贝叶斯信息准则来估计其分布类型及分布参数,以确定的概率分布形式表示稀疏混合不确定变量,便于后续设计过程中可靠度指标及失效概率求解.
(2)建立了一种基于Chebyshev逼近优化的响应边界求解方法. 针对产品设计中不确定变量计算结果失真问题,功能函数使用Chebyshev逼近并将稀疏混合不确定变量作为未知参数,获取Chebyshev多项式在已知区间变量的极值,采用改进的HL-RF算法对功能函数迭代求解,获取功能函数的可靠性指标、失效概率及对应的设计变量最优解.
(3)将提出的方法应用于高速压力机关键部件滑块的优化设计,与传统的区间分析方法对比,在满足设计需求的条件下,本文提出的方法获取的最优设计变量构造的数字样机质量更轻,并且应力分布改善,有利于滑块的轻量化和刚度保持设计.
参考文献
Reliability sensitivity estimation of nonlinear structural systems under stochastic excitation: a simulation-based approach
[J].
A density-matching approach for optimization under uncertainty
[J].
A modified reliability index approach for reliability-based design optimization
[J].
Reliability-based optimization using evolutionary algorithms
[J].DOI:10.1109/TEVC.2009.2014361 [本文引用: 1]
Reliability-based multi-objective optimization for automotive crashworthiness and occupant safety
[J].
Direct reliability-based design optimization of uncertain structures with interval parameters
[J].
Stochastic finite elements of discretely parameterized random systems on domains with boundary uncertainty
[J].
Robust optimization of uncertain structures based on normalized violation degree of interval constraint
[J].
Structural reliability analysis based on random distributions with interval parameters
[J].
A hybrid reliability approach based on probability and interval for uncertain structures
[J].
A sequential nonlinear interval number programming method for uncertain structures
[J].DOI:10.1016/j.cma.2008.04.027 [本文引用: 1]
时变可靠性的区间PHI2分析方法
[J].
The interval PHI2 analysis method for time dependent reliability
[J].
A new reliability analysis method for uncertain structures with random and interval variables
[J].DOI:10.1007/s10999-012-9184-8 [本文引用: 1]
Response-surface-based structural reliability analysis with random and interval mixed uncertainties
[J].DOI:10.1007/s11431-014-5581-6 [本文引用: 1]
Reliability-based design optimization of an automotive structure using a variable uncertainty
[J].DOI:10.1177/0954407015606825 [本文引用: 1]
Unified uncertainty representation and quantification based on insufficient input data
[J].DOI:10.1007/s00158-017-1722-4 [本文引用: 1]
Hybrid reliability analysis with uncertain statistical variables, sparse variables and interval variables
[J].
Likelihood-based representation of epistemic uncertainty due to sparse point data and/or interval data
[J].DOI:10.1016/j.ress.2011.02.003 [本文引用: 1]
Distribution type uncertainty due to sparse and imprecise data
[J].DOI:10.1016/j.ymssp.2012.07.008 [本文引用: 1]
Counterexamples to parsimony and BIC
[J].DOI:10.1007/BF00053369 [本文引用: 2]
A Chebyshev interval method for nonlinear dynamic systems under uncertainty
[J].DOI:10.1016/j.apm.2012.09.073 [本文引用: 1]
Interval multi-objective optimization of structures based on radial basis function, interval analysis, and NSGA-Ⅱ
[J].