目前被称作“第3次工业革命”^[1]的“3D打印技术”在建筑行业正引起广泛的关注. 在研究的过程中发现，“建筑3D打印”的主要关键点是喷头结构和材料性质^[2]，其中打印喷头可以通过旋转的单螺杆机构来提高水泥浆体的挤出效率；材料的性质主要取决于水灰及添加剂之间的配比量，根据不同配比下所表现的不同流体性质，浆体主要分为牛顿流体和非牛顿流体. 其中对于牛顿流体的研究已经成熟，而对于非牛顿流体的研究正引起广泛关注. 然而在非牛顿流体的研究中，使用传统的计算流体力学方法（如有限单元法、有限差分法等）存在算法复杂、对复杂边界处理能力不足从而影响计算精度等缺点，使用格子玻尔兹曼方法（lattice Boltzmann method，LBM）进行模拟是一种行之有效的方法^[3-4].

Aharonov等^[5]将松弛时间与黏度联系起来，将LBM应用到非牛顿流体的研究中. Boek等^[6]将LBM应用于管道流量试验中，对单相非牛顿流体流动进行研究，发现仿真结果与理论结果吻合较好. Malaspinas等^[7]使用局部分析法研究幂律流体，发现其稳定性与幂律指数有重要的关系. d'Humières^[8]在三维空间里对MRT-LBM模型进行了详尽的描述，并通过模拟对角型腔流的流动证明了该方法的稳定性和效率；Chai等^[9]提出了用于广义牛顿流体的MRT-LBM模型，并通过与解析解的比较和一些报告的数值结果进行验证，进一步证明了该法的稳定性及精确性. Fallah等^[10]利用MRT-LBM模型研究了旋转圆柱的流动场，并将模拟结果与之前的实验和数值数据进行比较，分析了转筒速度对流场速度分布的影响.

打印喷头输送的是不可压缩的黏塑性水泥浆，而水泥浆其黏性大、易黏连使输送受阻，因此为保证水泥浆输送的平稳性和连续性，研究水泥浆在螺槽中的流动情况十分必要. 鉴于水泥浆的黏度是变化的，本文在多松弛参数格子玻尔兹曼方法（multiple-relaxation-time lattice Boltzmann method，MRT-LBM）的基础上提出一种修正方法，使分析结果更加精确和稳定. 采用修正后的MRT-LBM模型对水泥浆在喷头中的流动情况进行模拟，分析水泥浆体的速度分布. 最后借助泊肃叶流验证所提模型的精确性和稳定性，通过对比解析解对修正后的MRT-LBM模型进行详细说明.

在水泥3D打印过程中，由于水泥浆体从喷头挤出到打印平台这段时间里没有模具维持挤出的形状，要求水泥浆体能迅速凝结硬化且具备一定的强度，同时要保证水泥浆体在喷头里具备一定的流动性. 建筑3D打印中常用的材料组成为普通硅酸盐水泥材料、骨料（粗砂、细砂等）以及一些辅助成型的添加剂（减水剂、速凝剂、引气剂等）^[11-12]. 实验中所用成型材料主要为普通硅酸盐水泥（52.5型江南小野田水泥）、直径为1 mm的普通黄沙、水、减水剂（聚羧酸）和速凝剂（十八水硫酸铝）；按照1∶1.2∶0.4∶0.001∶0.12的比例配制水泥浆体. 通过此配比来确定水泥浆体的流变方程.

大量研究发现，当室温、添加剂、水灰质量比不同时，水泥浆体的流体性质也不相同^[13]. 总体而言，水泥浆体主要有4种流变模型：宾汉流体、Herschel-Bulkley流体、幂律流体和牛顿流体；在室温为20 °C、水灰质量比为0.4~0.6时呈现出明显的幂律特性^[14]. 为了获取水泥浆体的流变模型，利用德国BRABENDER公司生产的Lab-Station W50EHT-3zone型转矩流变仪进行实验测试，实验温度为室温20 °C. 分别采用上述4种流变模型进行拟合，并通过拟合相关系数R²判断模型是否可作为水泥浆体的流变模型；通过对比4种流变模型的拟合程度发现幂律流体的拟合系数R²=0.984 3. 宾汉流体、Herschel-Bulkley流体和牛顿流体的拟合相关系数R²则比较低，通过进一步的流变曲线拟合得出水泥浆体的流变方程：

(1) $\tau = 1.667\;{\dot \gamma ^{0.578}}.$

式中：τ为切应力， $\dot \gamma $ 为剪切速率.

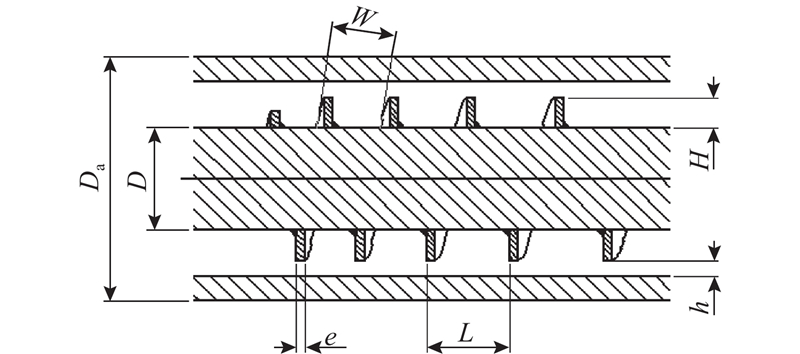
在打印过程中，水泥浆体流经如图1所示的螺旋槽区域；其中，h为螺杆与套筒的间隙，H为螺旋槽深度，W为螺槽宽度，L为节距，D为螺杆管径，D_a为螺筒管直径，e为螺棱的宽度.

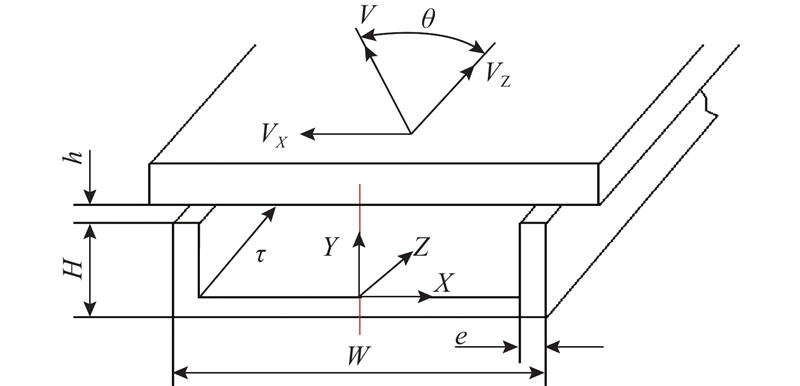
为研究水泥浆体在螺槽内的流动情况，上述结构可以进一步简化为螺槽展开模型. 由于螺杆是在套筒内以恒定转速N转动，根据运动的相对性，假设螺杆静止，将套筒以相同速度反转，进而将整个螺杆展开，即形成一个方腔. 其中Z方向为螺槽展开后指向出口方向，Y方向为螺杆径向方向，X方向为垂直螺棱方向，各部分运动关系、相应的坐标及尺寸关系如图2所示. 图中，θ为螺旋角，v为流动速度在侧棱壁面上的分量，τ为流体驱动力。

MRT-LBM模型的控制方程^[15]为

(2) $\begin{split} {{f}}\Big( {{r}} + &{{ { e} }_i}\delta t, {{r}} + \delta t \Big) - {{f}}\Big( {{{r}}, t} \Big) = \\ -& {{{M}}^{ - 1}}\bar {{S}}{{M}}\left[ {{{f}}\left( {{{r}}, t} \right) - {{{f}}^{\rm eq}}\left( {{{r}}, t} \right)} \right]. \end{split} $

式中： ${{f}}\left( {{{r}}, t} \right)$ 为密度分布函数， ${f^{\rm eq}}\left( {r, t} \right)$ 为平衡态分布函数，r为一个格子节点，t为时间， $\Delta t$ 为时间步长； ${{ e} _i}$ 为单位速度；M为变换矩阵，通过M可得到矩空间：

$ \varrho \left( {{{r}}, t} \right) = {{M}}{{f}}\left( {{{r}}, t} \right),\;{\varrho ^{\rm eq}}\left( {{{r}}, t} \right) = {{M}}{{{f}}^{\rm eq}}\left( {{{r}}, t} \right); $

碰撞松弛矩阵 $\overline {{S}} $ 为对角矩阵，

(3) $\overline {{S}} = {\rm diag}\left( {{s_0}, {s_1}, {s_2}, {s_3}, {s_4}, {s_5}, {s_6}, {s_7}, {s_8}} \right). $

令s₀=s₃=s₅=0，s₇、s₈是与运动黏度系数有关的因子，令s₇=s₈=1/τ；s₁是与体积黏性有关的元素，令s₁=s₂=1.35、s₄=s₆=1.12.

与Boltzmann方程碰撞项的近似模型（Bhatnagar-Gross-Kross，BGK）一样，MRT模型的演化过程也分为碰撞步和迁移步2个部分. 但不同于BGK模型，MRT模型的碰撞步在矩空间中执行，其方程为

(4) ${{{f}}^ + }\left( {{{r}}, t} \right) = {{f}}\left( {{{r}}, t} \right) - {{{M}}^{ - 1}}\overline {{S}} \left[ {\varrho \left( {{{r}}, t} \right) - {\varrho ^{\rm eq}}\left( {{{r}}, t} \right)} \right]. $

式中： ${{{f}}^ + }\left( {{{r}}, t} \right)$ 为碰撞后的密度分布函数. MRT模型的迁移步是在速度空间中进行，其方程为

(5) ${{f}}\left( {{{r}} + {{{e}}_i}\;\delta t, t + \delta t} \right) = {{{f}}^ + }\left( {{{r}}, t} \right). $

MRT模型除了在矩空间进行交换，还在速度空间进行交换. 因此，通过Chapman-Enskog扩展理论，可以得到运动黏度 $\mu $ 的数学模型：

(6) $\mu = \rho \nu = \rho c_{\rm s}^2\left( {\frac{1}{{{s_8}}} - \frac{1}{2}} \right)\delta t.$

式中： $\nu $ 为动力黏度； $c_{\rm s}^{}$ 为格子声速；也可以得到密度 $\rho $ 和速度 $u$ 的数学模型，即：

(7) $\rho = \sum\limits_{i = 0}^8 {{f_i}\left( {r, t} \right)},\;\; \rho u = \sum\limits_{i = 0}^8 {{c_i}{f_i}\left( {r, t} \right)} .$

式中：c_i为速度向量，f_i为密度分布函数，i=0, 1, ···，8，对应8个方向。

鉴于剪切速率或速度梯度的变化会影响到运动黏度的变化，在处理运动黏度时，需要建立一种合适的差分格式. 有限差分法繁琐复杂，而使用LBM可以简化求解过程. 例如：BGK模型中的应变率张量 ${{{S}}_{\alpha \beta }}$ 可以通过在每个节点上进行局部计算得到^[16]：

(8) $\begin{split} {{{S}}_{\alpha \beta }} = & - \frac{1}{{2\rho c_{\rm s}^2{\tau _{\rm BGK}}{\Delta t}}} \\ & \left[ {\sum\limits_{i = 0}^8 {{{{e}}_{i\alpha }}{{{e}}_{i\beta }}\left[ {{{{f}}_i}\left( {{{r}}, t} \right) - {{{f}}_j}^{\rm eq}\left( {{{r}}, t} \right)} \right]} } \right]. \end{split} $

在MRT模型中，通过下式可以得到应变速率张量^[17-18]：

(9) $\begin{aligned} {{{S}}_{\alpha \beta }} = & - \frac{1}{{2\rho c_{\rm s}^2{\Delta t}}} \\ & \left[ {\sum\limits_{i = 0}^8 {{{{e}}_{i\alpha }}{{{e}}_{i\beta }}\sum\limits_{j = 0}^8 {{{\left( {{{{M}}^{ - 1}}\bar {{S}} {{M}}} \right)}_{ij}}\left( {{{{f}}_j}\left( {{{r}}, t} \right)-} \right.} } } \right. \left. { \left. {{{f}}_j^{\rm eq}\left( {{{r}}, t} \right)} \right)} \right]. \end{aligned} $

由上文可知，对于非牛顿流体模型的仿真，在应用过程中影响MRT-LBM的主要因素为局部松弛时间，也可以理解为MRT-LBM主要受与应力张量和应变张量有关的黏度的影响. 对于常见的非牛顿流体，其应力张量 ${{{\sigma}} _{ij}}$ 和应变张量D_ij的关系与牛顿流体的关系是类似的，即 ${{{\sigma}} _{ij}} = 2\mu {{{D}}_{ij}}$. 对非牛顿流体中广泛使用的幂律流体来说，局部剪切速率 $\dot \gamma $ 的大小与应变张量有关，即 $\dot \gamma = \sqrt {{{{D}}_{ij}}{{{D}}_{ij}}} $. 但是使用LBM直接分析幂律流体存在一定困难，这是因为在剪切变稀型流体中，当剪切率为0时，有效黏度为无穷大；而在剪切增稠型流体中，当剪切率为0时，有效黏度为0. 事实上许多非牛顿流体只在一定剪切率内表现出幂律特性，在这个范围之外黏度是恒定的. 因此这里对幂律流体模型提出一种修正MRT-LBM模型，即分段幂律模型：

(10) $\nu \left( {\dot \gamma } \right){ { = }}\frac{{\mu \left( {\dot \gamma } \right)}}{\rho }{ { = }}\left\{ \begin{array}{l} \!\!m\dot \gamma _0^{\left( {n - 1} \right)},\; \dot \gamma \leqslant {{\dot \gamma }_0} ;\\ \!\! m{{\dot \gamma }^{\left( {n - 1} \right)}},\; {{\dot \gamma }_0} \leqslant \dot \gamma \leqslant {{\dot \gamma }_\infty } ;\\ \!\!m\dot \gamma _\infty ^{\left( {n - 1} \right)}, \;\dot \gamma \leqslant {{\dot \gamma }_\infty }. \end{array} \right.$

式中：m为流体黏度系数，n为幂律指数，γ₀为截断的幂律流体模型中的低剪切速率，γ_∞为高剪切速率.

鉴于MRT-LBM可以在有限的动力黏度范围内精确地模拟黏性流体，当松弛时间 $\tau \leqslant 0.5$ 时（运动黏度变得很小），此方法变得不稳定^[19]；当松弛时间 $\tau \geqslant 1.0$ 时（运动黏度变得较大），模拟精度也会随之变得很差^[20]. 由此可以看出，过小或过大的动力黏度都会造成模拟精度变差或使得稳定性变差. 很显然，在剪切变稀形流体中黏度的最大值与零剪切率对应，在剪切增稠型流体中黏度最小值与零剪切率对应.

由前文可知，可将螺杆结构展开成矩形腔体，转换成研究水泥浆体在矩形腔体里的流动可以使问题简化. 对螺杆展开图（见图2），采用D2Q9模型，这里只对上表面设置速度，速度方向为y=H处的x方向，其余壁面的速度设为0. 结合喷头的扫描速度和水泥浆体的凝固时间确定整个流动区域的大小，矩形面的各处尺寸为W=24 mm，H=12 mm，考虑到打印过程的实际情况，将螺杆的旋转速度设为40 r/min，螺杆的导程角θ=20°. 利用相似运动原理，取雷诺数Re为关键准则数进行量纲转换，从而得到仿真模型中的各个参数. 通过上文分析可知，黏度是影响精度与稳定性的主要参数，因此最后通过修正黏度对模拟过程进行精度的调节.

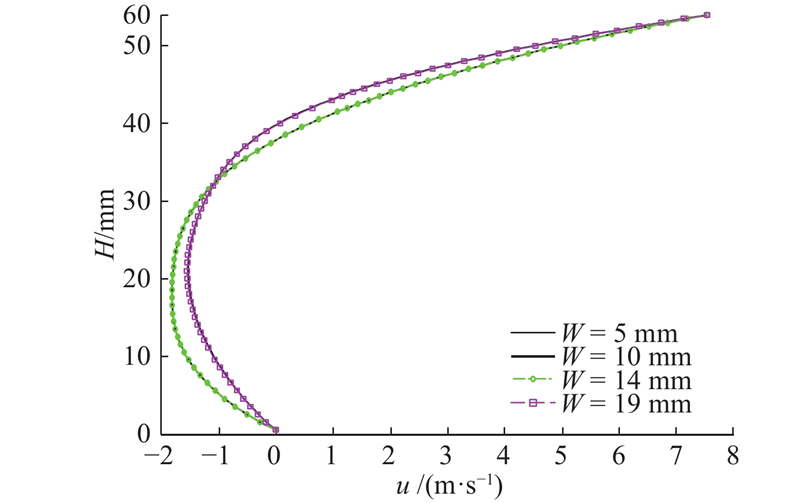
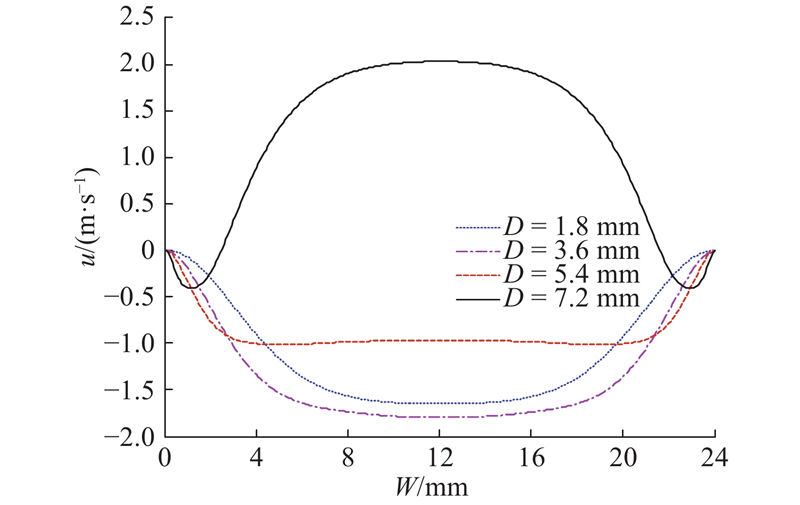
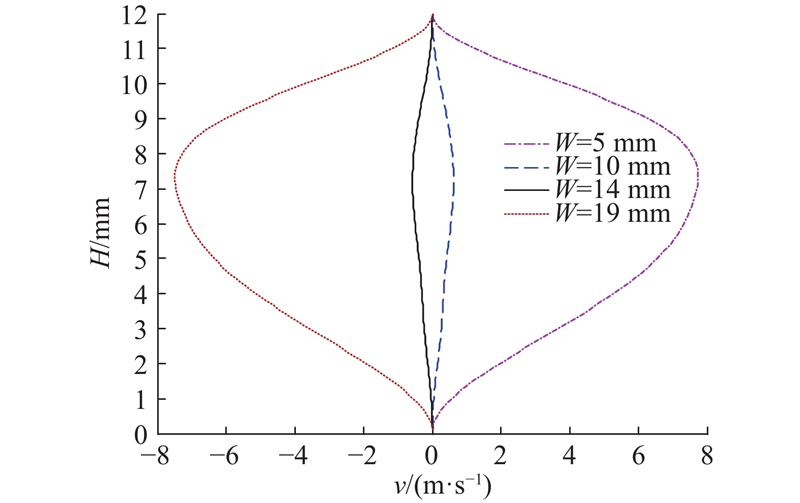
对于速度场的分布情况，运用MRT-LBM修正模型进行模拟，即在格子数相同情况下，对螺槽内不同位置处的速度进行计算和对比分析。水泥浆体在螺杆截面的速度分布特征如图3~6所示；从图3中可以看出，速度分量u在靠近套筒壁和螺槽上部的这段范围内急剧减小，在螺槽的中段到螺槽底面速度分量u（宽度方向）减小的速度变缓；另外在沿深度H的方向上速度分量u在螺槽不同宽度位置变换基本一致. 图4显示，在螺槽的左、右槽棱处的速度分量u趋于0，即在螺槽的左、右角落流动特性不明显且对称分布；速度分量u自左、右螺棱向螺槽中间位置逐渐增加，在螺槽中部流速平稳. 图5显示，从宽度方向上看，在螺槽的中间位置速度分量v（深度方向）趋于0，在靠近螺棱的位置存在不为0的速度分量v；而且在W=5 mm和19 mm时速度分量v出现峰值；从深度方向上看，靠近套筒壁与螺杆壁的部位速度分量v=0. 图6中速度分量v的变化趋势是从螺槽左、右槽棱处向着螺槽中部逐渐减小为0，综合图4~6还可以发现，在螺槽的左、右底角部位流动特性不明显，基本没有流动速度.

为验证修正MRT-LBM模型在模拟非牛顿流体时的可行性、精确性和稳定性，以已有理论解的泊肃叶流为例进行详细分析. 将2个平行板之间的距离定义为b、方向设为y；压力梯度 $\nabla p=\partial p /\partial x $ 作用在x方向上；u_y是y方向上的一个非零速度分量. 为求分段幂律模型在压力驱动下的Navier-Stokes方程精确解，将平行平板流的y方向分为2个对称区域[−b/2，0]和[0，b/2]. 只讨论[0，b/2]的速度分布即可得到整个区域的分布情况（对称性）. 将区域[0，b/2]划分成3个不同的区域，第1个区域是靠近流道中心的低剪切率L区域，即 $0 \leqslant y \leqslant {y_{\rm l}}$，该区域内剪切速率小于 ${\dot \gamma _0}$，并且流体的性质可以看作是牛顿流体，动力黏度 ${\nu _0} = m{\dot \gamma _0}^{(n - 1)}$. 第2个区域是式（10）中幂律流体的I区域，即 ${y_{\rm l}} \leqslant y \leqslant {y_{\rm h}}$；最后1个是靠近壁面的高剪切率H区域，即 ${y_{\rm h}} \leqslant y \leqslant h/2$，在这个区域内剪切速率超出了 ${\dot \gamma _\infty }$，流体可看成是具有有效运动黏度的牛顿流体 ${\nu _\infty } = m{\dot \gamma _\infty }^{(n - 1)}$. 将每个区域的解与速度和应力的连续性相匹配，在压力梯度 $\nabla p$ 作用下得到1个通解：

(11) ${u_y} = \left\{ {\begin{array}{*{20}{l}}{ - \frac{{\rm{1}}}{{\rm{2}}}\frac{{\rm{1}}}{{{v_0}}}\frac{{\partial p}}{{\partial x}}\left[ {{{\left( {b/{\rm{2}}} \right)}^2} - {y^2}} \right],\;\;\;\;\;\;\;\;\;\;0 \le y \le {y_{\rm{l}}};}\\{\frac{n}{{n + 1}}{{\left( { - \frac{1}{m}\frac{{\partial p}}{{\partial x}}} \right)}^{1/n}} \times }\\{\left[ {{{\left( {b/{\rm{2}}} \right)}^{\frac{n}{{n + 1}}}} - {y^{\frac{n}{{n + 1}}}}} \right] + {\alpha _1},\quad {\kern 1pt} {\kern 1pt} \;\;\;\;\;\;\;\;\;\;\;\;\;{y_{\rm{l}}} \le y \le {y_{\rm{H}}};}\\{ - \frac{{\rm{1}}}{{\rm{2}}}\frac{{\rm{1}}}{{{v_\infty }}}\frac{{\partial p}}{{\partial x}}\left[ {{{\left( {b/{\rm{2}}} \right)}^2} - {y^2}} \right] + {\alpha _2},\;\;\;\;\;\;\;\;\;{y_{\rm{H}}} \le y \le b/2.}\end{array}} \right.$

式中：常数项 ${\alpha _1}{\text 、}{\alpha _2}$ 的表达式如下，

(12) $ \begin{array}{*{20}{l}}{{\alpha _1} = - \frac{{\rm{1}}}{{\rm{2}}}\frac{1}{{{v_0}}}\frac{{\partial p}}{{\partial x}}\left[ {{{\left( {b/{\rm{2}}} \right)}^2} - {y^2}} \right] - }\\{\qquad \frac{n}{{n + 1}}{{\left( { - \frac{1}{m}\frac{{\partial p}}{{\partial x}}} \right)}^{{\rm{1}}/n}}\left[ {{{\left( {b/{\rm{2}}} \right)}^{({\rm{1 + 1}}/n)}} - y_{\rm{l}}^{({\rm{1 + 1/}}n)}} \right],}\end{array} $

(13) $\begin{array}{l}{\alpha _2} = \frac{n}{{n + 1}}{\left( { - \frac{1}{m}\frac{{\partial p}}{{\partial x}}} \right)^{{\rm{1}}/n}}\left[ {{{\left( {b/{\rm{2}}} \right)}^{(1 + 1/n)}} - y_{\rm{h}}^{(1 + 1/n)}} \right] - \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\rm{1}}}{{\rm{2}}}\frac{1}{{{v_\infty }}}\frac{{\partial p}}{{\partial x}}\left[ {{{\left( {b/{\rm{2}}} \right)}^2} - y_{\rm{h}}^2} \right] + {\alpha _1}.\end{array}$

将速度分布函数求导，由松弛时间τ相等可知：

(14) $ \left. {\begin{array}{*{20}{l}}{{y_{\rm{l}}} = v_0^{\frac{n}{{n - 1}}}/\left[ {{m^{\frac{1}{{n - 1}}}}( - \partial p/\partial x)} \right],}\\{{y_{\rm{h}}} = v_\infty ^{\frac{n}{{n - 1}}}\left[ {{m^{\frac{1}{{n - 1}}}}( - \partial p/\partial x)} \right].}\end{array}} \right\}$

由式（14）可以看出，区域y的大小取决于式中不同参数值的大小. 为验证此截断模型下不同幂律指数的有效性及稳定性，需要对不同的幂律指数n进行模拟. 本文中研究剪切变稀型流体（n=0.5）和剪切增稠型流体（n=2.0）在距离b=10 mm的平板之间的速度分布情况. 当n=0.5时，取压力梯度 $\nabla p = - 2.5 \times {10^{ - 6}}$，运动黏度 ${\nu _\infty } = 0.001$，流体黏度系数 $m = {10^{ - 3}}$，格子数N=400，从而可以得到LBM求出的结果. 然后将其与式（11）分析得到的结果进行对比，如图7(a)所示，粗实线反映了LBM得到的结果，虚线部分是通过式（11）分析得到的结果，垂直虚线是在低剪切速率区域L和中间剪切速率区域I之间的过渡点. 当取幂律指数n=2时，取压力梯度 $\nabla p = - 5 \times {10^{ - 4}}$，运动黏度 ${\nu _0} = 0.001$， ${\nu _\infty } = 0.1$，流体黏度系数 $m = {10^{ - 3}}$，格子数N=400，得到数值分析结果与仿真的结果对比图如图7(b)所示.

对比图7(a)和(b)可知，曲线之间的重合度非常好. 另外通过改变晶格节点的数量（N=10~500），计算LBM结果与理论结果的相对误差：

$ R = \displaystyle\sum\limits_{i = 1}^N {{{\left( {1 - \nu _i^{\rm LBM}/\nu _i^{\rm anal}} \right)}^2}} .$

通过对不同幂律指数下的流体进行仿真可以发现，在格子增加的过程中，实验结果和理论结果的误差值在逐渐降低；虽然不同的幂律指数对应不同的误差变化趋势。但是在不断增加格子数目的情况下误差总能保持在0.01%之内.

（1）在工程应用实例中，采用MRT-LBM修正模型模拟水泥浆体在单螺杆挤出机构里的流动情况，得到速度场分布情况. 为了保证打印的连续性和稳定性，可以通过增加螺杆旋转速度和扩大螺槽槽宽来增加水泥浆体在喷头机构里的流动速度.

（2）对于螺槽槽底左、右两处流动不明显的情况，可以将螺棱与底面的夹角由直角改为钝角，即将矩形截面改成梯形截面.

（3）使用泊肃叶流验证了通过数学推导出的通解公式，将解析解与MRT-LBM修正模型得到的结果进行对比，发现两者误差很小，证明了MRT-LBM修正模型的可行性，并且发现在使用此方法模拟时，当格子数增加后，仿真误差逐渐减小，进一步说明了使用MRT-LBM修正模型可以避免未修正模型在仿真过程中出现的不精确与不稳定情况.