近年来,国内外许多学者对换流变压器绝缘结构极性反转电场进行了研究. 吕晓德等[3]用反转前阻性分布电场与反转后容性分布的2倍负极性激励电场叠加得到极性反转电场;Wen等[4-5]应用状态空间有限元法、梯形公式分析各向同性线性媒质下的极性反转电场;李琳等[6]应用龙格库塔法计算各项异性非线性媒质中的极性反转电场分布. 以上研究都着眼于电场强度的计算,并且是在粗略假设空间电荷的基础上解释极性反转瞬间的电场突变,对于极性反转结果,只能得到电位及电场强度的分布情况,未能分析空间电荷的变化规律. Huang等[7-8]利用电声脉冲法(pulsed electro-acoustic, PEA)分别研究电压极性、反转时间等对单层油浸纸内部电荷积聚的影响和油-油浸纸绝缘的反转电场畸变规律,得到极性反转下的电荷动态变化,但主要集中在试验测量方面,对数值计算方法方面未有涉及.
将瞬态上流元法应用于多类型油纸绝缘介质极性反转电场分析,并引入界面势垒模型,研究极性反转电压下单层油浸纸和油浸纸-油双层绝缘介质内部空间电荷随加压时间的动态分布特性,并根据电荷密度分布分析电压反转瞬间的瞬态电场分布及变化规律,计算精度较高. 仿真结果对换流变压器绝缘水平和击穿特性研究具有参考价值.
1. 模型描述
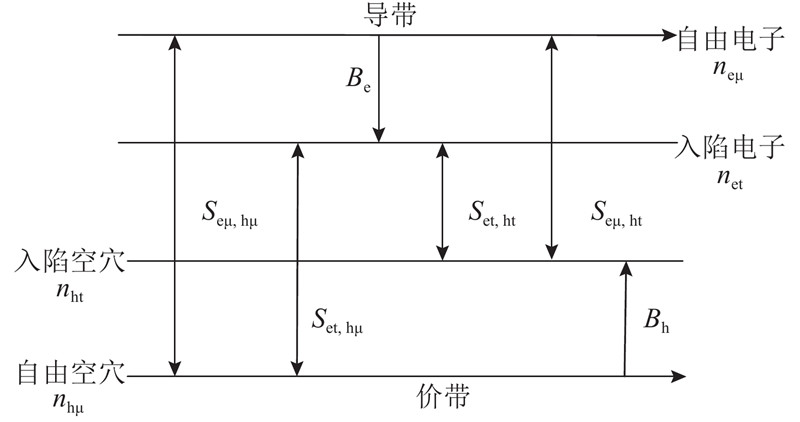
基于肖特基电极注入和双极性空间电荷输运建立数学模型[12],同时将电荷的运动、复合和入陷引入模型计算.
空间电荷的输运和瞬态电场满足以下控制方程:
式中:
1.1. 肖特基发射和输运
对于空间电荷的产生,介质内部的带电粒子主要是电子和空穴,分别代表正电荷和负电荷. 在直流电场的作用下,金属表面载流子的逸出势垒降低,从金属表面热电子发射到介质内部的载流子增多,这就是肖特基注入效应[13]. 金属表面注入电流密度方向垂直于金属表面,其幅值的计算公式为
式中:J(t)为阴极表面注入电子或阳极表面注入空穴产生的电流密度;T为开氏温度;A为Richardson常数,取120 A/(cm2·K2);ωi为电子或空穴的注入势垒;E(t)为金属表面的电场强度;k为普朗克常数;e为电子的电荷量,e=1.602 189 2×10−19 C;ε为介质介电常数.
图 1
图 1 载流子传输、复合和入陷模型
Fig.1 Model of carrier transport, recombination and trapping
此时,考虑载流子的变化,电流连续性方程可以描述为
式中:
式中:
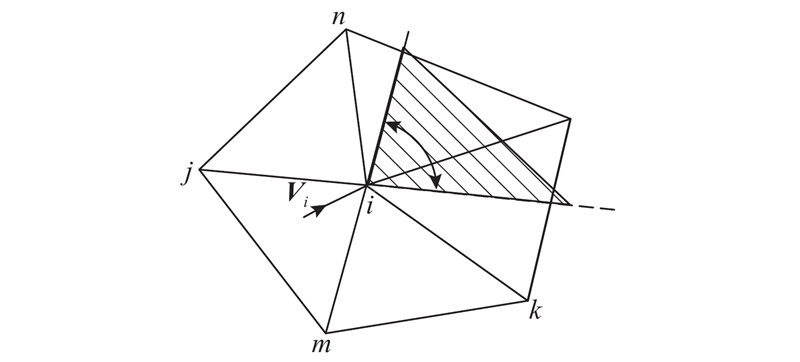
1.2. 瞬态上流元法
图 2
式中:μ为电子或空穴在介质中的迁移率,将载流子在同一种介质中的迁移率视为恒定常数.
若节点电荷密度已知,通过求解泊松方程可以得到介质内部电场分布. 相反地,如果已知电场求解电荷密度,将式(1)、(3)、(10)代入式(5)中,可以得到
式中:
对式(11)在时间t=tn处进行离散,根据下述电荷密度更新公式可得到节点i在t=tn+1时刻的电荷密度:
式中:tn、tn+1为相邻的时间步,
式中:N1、N2、N3分别为节点i、j、m的对应形状函数.
由于方程差分格式的稳定性受时间步长和空间离散单元的大小影响较大,为了同时保证收敛性和求解效率,在仿真中设置迭代时间步长为1 s.
1.3. 仿真条件
采用与文献[11]相同的油纸绝缘材料参数设置,如表1所示. 表中,
表 1 油纸绝缘材料仿真参数设置
Tab.1
| 参数 | 单位 | 数值 |
| 电子迁移率μe | m2/(V∙s) | 1×10−14 |
| 空穴迁移率μh | m2/(V∙s) | 1×10−14 |
| 电子陷阱捕获系数Be | s−1 | 5×10−3 |
| 空穴陷阱捕获系数Bh | s−1 | 5×10−3 |
| 电子陷阱浓度Net0 | C/m3 | 100 |
| 空穴陷阱浓度Nht0 | C/m3 | 100 |
| 复合系数(自由电子/入陷空穴)Seμ,ht | m−3∙C−1∙s−1 | 5×10−2 |
| 复合系数(入陷电子/自由空穴)Set,hμ | m−3∙C−1∙s−1 | 5×10−2 |
| 复合系数(自由电子/自由空穴)Seμ,hμ | m−3∙C−1∙s−1 | 0 |
| 复合系数(入陷电子/入陷空穴)Set,ht | m−3∙C−1∙s−1 | 5×10−2 |
| 电子肖特基注入势垒ωei | eV | 1.1 |
| 空穴肖特基注入势垒ωhi | eV | 1.1 |
| 温度T | K | 293.2 |
| 油相对介电常数εi | − | 2.5 |
| 油浸纸相对介电常数εop | − | 3.5 |
图 3
2. 仿真结果与分析
2.1. 单层油浸纸模型仿真结果分析
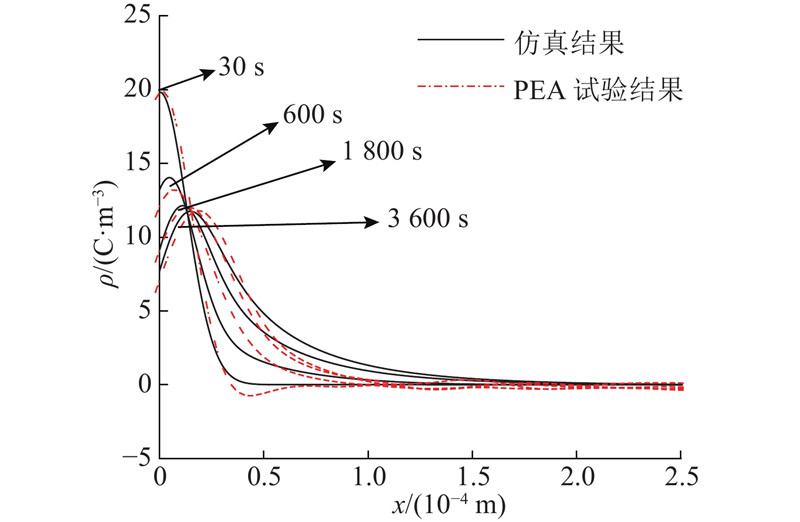
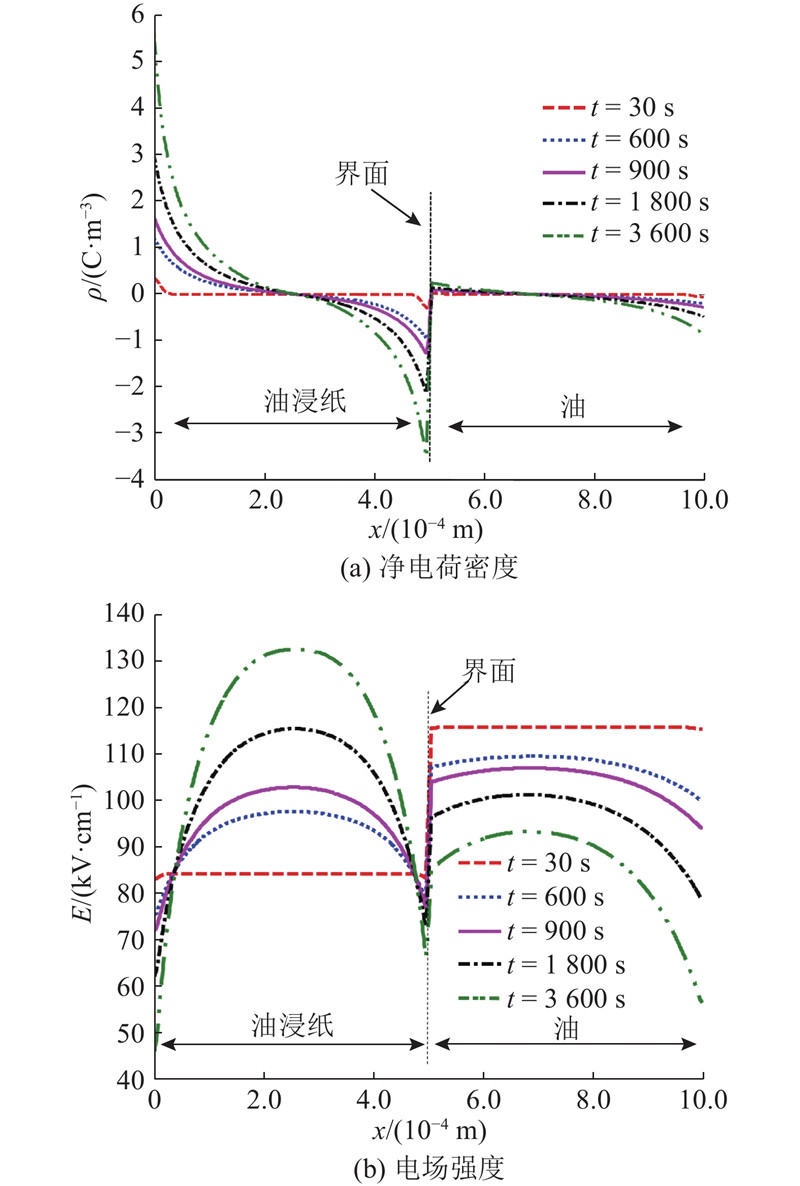
测量端在正极板侧,附近电荷密度测量精度较高,因此取图4中路径1上靠近正极板侧250 μm的电荷密度分布(见图5). 该仿真结果与PEA测量结果吻合较好[19]. 从仿真结果可以看出,在稳态直流电压作用下,同极性空间电荷积聚于极板附近,并随着时间的推移向介质内部迁移,大约在3 600 s时刻介质内部电荷运动基本达到稳定,此时电荷密度计算误差为0.19‰. 在稳态时刻(t=3 600 s),将电压极性进行反转,得到电压反转瞬间及反转后各个时刻路径1上的净电荷密度和场强(见图6). 反转完成后,极板周围的电荷来不及立即消散,极板周围仍积聚大量电荷. 极板场强较大,使得肖特基发射产生的载流子增多,其与极板附近积聚的大量电荷极性相反,从而发生复合,因此极板附近的净电荷浓度迅速减小并很快改变极性,而后相反极性电荷浓度不断增加. 电荷之间的复合作用,使其对极板电场的畸变减弱,肖特基发射的电荷也相应减小,因此净电荷浓度和场强随时间的变化率也逐渐减小并逐步重新达到稳定状态. 稳态时极板电荷密度为−27.3 C/m3,相应地,极板场强减小为−43.7 kV/cm,小于介质内部电场. 上述规律与文献[8]中通过PEA试验得到的结论一致.
图 5
图 5 单层油浸纸在路径1上的电荷密度分布仿真结果与试验结果对比
Fig.5 Comparison of charge densities simulation and experiment results of single-ayer oil impregnated paper along path one
图 6
图 6 极性反转下单层油纸内部电荷及电场分布
Fig.6 Charge distribution and electric field in single-layer model under polarity reversal voltage
图 4
2.2. 油浸纸-油双层绝缘模型仿真结果分析
图 7
式中:
将载流子在油和油浸纸介质中的迁移率分别设为7×10−14、5×10−14 m2/(V∙s). 根据文献[22],由于正、负板分别和油、油浸纸2种不同介质接触,故空穴和电子的肖特基注入势垒不同,分别设置为1.10、1.15 eV. 同时,载流子穿过界面受到的阻碍更大,故设置界面的势垒略大于两侧极板的肖特基注入势垒.
由图8(b)可以看出,在初始时刻,由于空间电荷对电场的影响较小,油浸纸中电场小于油中电场,内部场强分别为83.3、116.7 kV/cm;而随着界面负电荷以及极板附近同极性电荷的积聚,油浸纸中的场强不断增大. 约1 000 s后油浸纸中的电场已经大于油中,稳态时两介质中心电场分别为132.6、93.3 kV/cm,此时极板附近的电场畸变也更严重,极板电场明显小于介质内部电场. 另外,界面处的场强随着负电荷积聚呈现不断减小的趋势,直至稳态.
图 8
图 8 稳态电压下双层介质中电荷和电场分布
Fig.8 Charge distribution and electric field in two-layer insulation under steady direct current
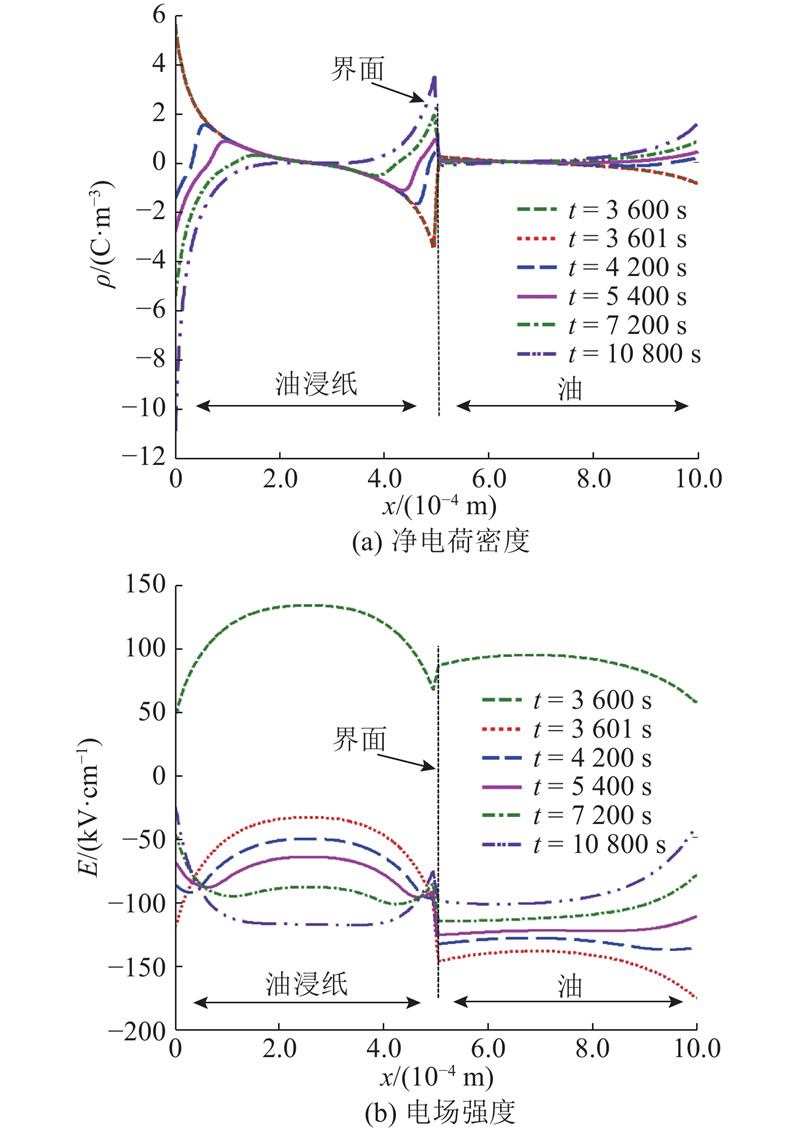
在反转完成后的一段时间内,由于负极板(油侧极板)附近场强小于正极板(油浸纸侧极板)附近场强,故肖特基注入的电子量小于空穴. 同时,空穴在油中的迁移率较大,于是不断运动到界面并与积聚的电子复合,使界面的负电荷不断减小,进而正极性电荷不断积累. 界面不断积聚的正电荷会逐渐加强油浸纸中的电场并削弱油中电场. 由图9(a)可以看出,在反转后约7 800 s时刻,界面积累的正电荷密度达到2.64 C/m3,导致油浸纸中的电场重新大于油中电场.
图 9
图 9 极性反转下双层介质中电荷和电场分布
Fig.9 Charge distribution and electric field in two-layer insulation under polarity reversal voltage
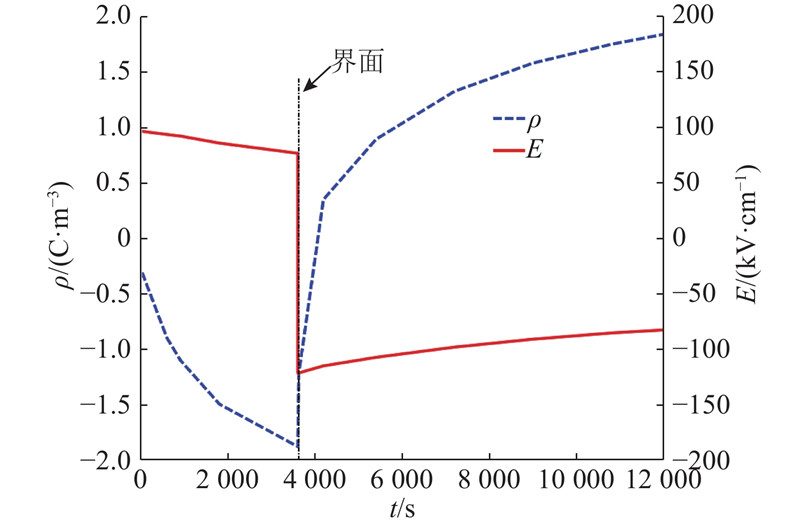
如图10所示为0 s时刻到12 000 s时刻,即整个反转电压施加过程中,界面电荷密度及场强随时间的变化曲线. 由图可以看出界面电荷逐渐积聚-消散-重新积聚的过程. 在电压反转瞬间,界面附近的电场增大,但相对于极板附近增幅较小. 反转完成后达到稳态时的界面电荷密度及场强(−1.82 C/m3、76 kV/cm)与反转前的稳态值(1.87 C/m3、−78 kV/cm)近似相等. 但是相比于单层油浸纸介质,双层油浸纸-油介质在电压反转后重新达到稳态需要更长的时间. 其原因有以下2点:油浸纸和油界面处的深陷阱和势垒使得电荷更不容易消散和运动;双层介质内部电场的不均匀性改变了两侧极板肖特基注入的电荷量,继而减慢了电荷的复合和重新分布进程.
图 10
图 10 界面电荷密度及场强随时间变化曲线
Fig.10 Variation of interfacial charge density and electric field with time
3. 结 论
采用瞬态上流元法(TUFEM)计算极性反转电压下单层油浸纸和油浸纸-油双层绝缘内部电荷的动态分布和瞬态场强. 主要结论如下:
(1)在10 kV直流电压反转瞬间,单层油浸纸介质在极板附近出现严重的电压畸变,瞬态场强可以达到368 kV/cm,是在无电荷存在情况下均匀场强的2倍多. 介质中心场强变化较小.
(2)在直流电压下,油浸纸-油双层介质的界面电荷不断积聚,介质中的电场从油大于油浸纸变为油浸纸大于油. 在电压反转后,界面电荷逐渐消散并重新积聚异极性电荷,反转后达到稳态时介质内部的电荷及电场分布与反转前的稳态近似镜像对称.
(3)在10 kV直流电压反转瞬间,在油浸纸-油介质的界面积聚电荷的影响下,油中出现强暂态高电场,场强最高达到176.87 kV/cm,约为稳态场强的3倍. 与单层油纸介质类似,场强极大值出现在极板附近,但最大值则出现在油侧极板.
(4)瞬态上流元法在计算油纸绝缘内电荷动态特性及其影响下的极性反转电场特性方面具有优势,精确度较高,可以为换流变压器内绝缘设计提供参考.
参考文献
油纸绝缘介质的空间电荷积聚与消散特性
[J].
Space charge phenomena in oil-paper insulation materials under high voltage direct current
[J].
变压器油纸绝缘介质在直流电场中的空间电荷输运特性
[J].
Space charge transport properties of oil-paper insulation materials under DC field used in transformer
[J].
换流变压器端部极性反转电场的数值算法及其绝缘设计
[J].
Numerical computation of polarity reversal electric field in the converter transformer ending and its insulation design
[J].
A calculation method and some features of transient field under polarity reversal voltage in HVDC insulation
[J].DOI:10.1109/61.180340 [本文引用: 1]
油纸绝缘结构瞬态电场计算的状态空间有限元法
[J].
A state space finite element method for calculation of transient electrical field in oil-paper insulation construction
[J].
换流变压器极性反转试验的数值模拟
[J].
Numerical simulation of converter transformer's polarity reversal test
[J].
Space charge characteristics in oil and oil-impregnated pressboard and electric field distortion after polarity reversal
[J].DOI:10.1109/TDEI.2015.005413 [本文引用: 2]
Influence of voltage reversal on space charge behavior in oil-paper insulation
[J].DOI:10.1109/TDEI.2013.004010 [本文引用: 2]
A model for bipolar charge transport, trapping and recombination in degassed crosslinked polyethene
[J].DOI:10.1088/0022-3727/27/6/029 [本文引用: 1]
Calculation of ion flow fields of HVDC transmission lines by the finite element method
[J].DOI:10.1109/TPAS.1981.316432 [本文引用: 1]
油-纸绝缘结构合成电场数值模拟方法研究
[J].
Numerical simulation of electric field considering space charge in oil-paper insulation
[J].
Description of bipolar charge transport in polyethylene using a fluid model with a constant mobility: model prediction
[J].DOI:10.1088/0022-3727/37/2/020 [本文引用: 1]
A new numerical model applied to bipolar charge transport, trapping and recombination under low and high DC voltages
[J].DOI:10.1088/0022-3727/40/21/041 [本文引用: 1]
极性反转时间对聚乙烯中空间电荷及瞬态电场的影响
[J].
Effect of voltage reverse time on space charge and transient field in polyethylene
[J].
Description of charge transport in polyethylene using a fluid model with a constant mobility: fitting model and experiments
[J].DOI:10.1088/0022-3727/39/7/014 [本文引用: 1]
直流电场下油纸绝缘介质界面处的空间电荷特性
[J].
Space charge characteristics of the interface in oil-paper insulation under DC voltage
[J].
温度梯度下油纸绝缘空间电荷特性的数值仿真
[J].
Numerical simulation of space charge property in oil-paper insulation under temperature gradient
[J].
Space charge behavior in the sample with two layers of oil-immersed-paper and oil
[J].DOI:10.1109/TDEI.2014.004241 [本文引用: 1]
直流电压下多层油纸绝缘介质的界面空间电荷特性
[J].DOI:10.3969/j.issn.1003-6520.2013.06.003 [本文引用: 1]
Interface space charge characteristics in multi-layer oil-paper insulation under DC voltage
[J].DOI:10.3969/j.issn.1003-6520.2013.06.003 [本文引用: 1]